Circuitos aritméticos
En el capítulo anterior, discutimos sobre las aplicaciones básicas del amplificador operacional. Tenga en cuenta que vienen bajo las operaciones lineales de un amplificador operacional. En este capítulo, analicemos los circuitos aritméticos, que también son aplicaciones lineales del amplificador operacional.
Los circuitos electrónicos, que realizan operaciones aritméticas se denominan como arithmetic circuits. Usando amplificadores operacionales, puede construir circuitos aritméticos básicos como unadder y un subtractor. En este capítulo, aprenderá sobre cada uno de ellos en detalle.
Sumador
Un sumador es un circuito electrónico que produce una salida, que es igual a la suma de las entradas aplicadas. Esta sección trata sobre el circuito sumador basado en amplificador operacional.
Un sumador basado en amplificador operacional produce una salida igual a la suma de los voltajes de entrada aplicados en su terminal inversor. También se llama comosumming amplifier, ya que la salida es amplificada.
los circuit diagram de un sumador basado en amplificador operacional se muestra en la siguiente figura:
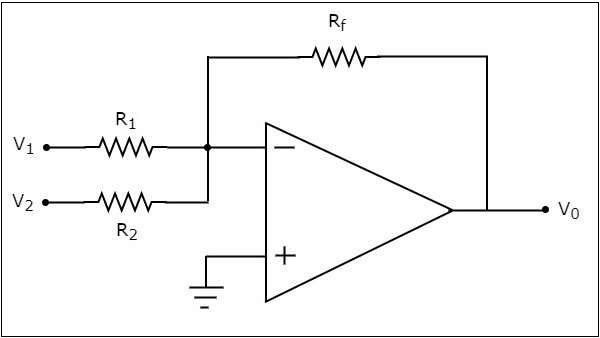
En el circuito anterior, el terminal de entrada no inversora del amplificador operacional está conectado a tierra. Eso significa que se aplica cero voltios en su terminal de entrada no inversora.
De acuerdo con la virtual short concept, el voltaje en el terminal de entrada inversora de un amplificador operacional es el mismo que el voltaje en su terminal de entrada no inversora. Entonces, el voltaje en el terminal de entrada inversora del amplificador operacional será cero voltios.
los nodal equation en el nodo del terminal de entrada inversora
$$ \ frac {0-V_1} {R_1} + \ frac {0-V_2} {R_2} + \ frac {0-V_0} {R_f} = 0 $$
$$ => \ frac {V_1} {R_1} - \ frac {V_2} {R_2} = \ frac {V_0} {R_f} $$
$$ => V_ {0} = R_ {f} \ left (\ frac {V_1} {R_1} + \ frac {V_2} {R_2} \ right) $$
Si $ R_ {f} = R_ {1} = R_ {2} = R $, entonces el voltaje de salida $ V_ {0} $ será -
$$ V_ {0} = - R {} \ izquierda (\ frac {V_1} {R} + \ frac {V_2} {R} \ derecha) $$
$$ => V_ {0} = - (V_ {1} + V_ {2}) $$
Por lo tanto, el circuito sumador basado en amplificador operacional discutido anteriormente producirá la suma de los dos voltajes de entrada $ v_ {1} $ y $ v_ {1} $, como salida, cuando todas las resistencias presentes en el circuito tengan el mismo valor . Tenga en cuenta que el voltaje de salida $ V_ {0} $ de un circuito sumador tiene unnegative sign, que indica que existe una diferencia de fase de 180 0 entre la entrada y la salida.
Sustractor
Un restador es un circuito electrónico que produce una salida, que es igual a la diferencia de las entradas aplicadas. Esta sección trata sobre el circuito sustractor basado en amplificador operacional.
Un sustractor basado en amplificador operacional produce una salida igual a la diferencia de los voltajes de entrada aplicados en sus terminales inversoras y no inversoras. También se llama comodifference amplifier, ya que la salida es amplificada.
los circuit diagram de un sustractor basado en amplificador operacional se muestra en la siguiente figura:
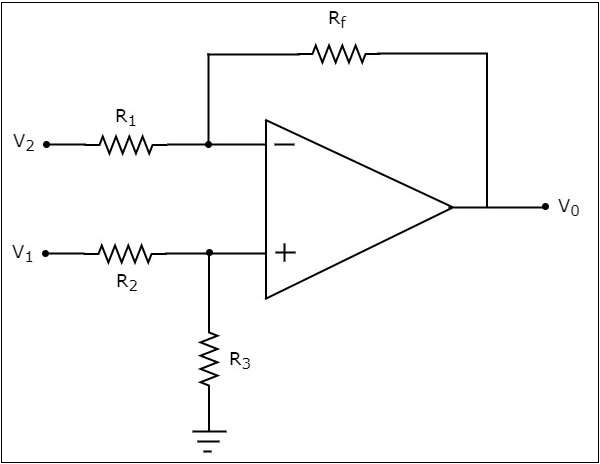
Ahora, busquemos la expresión para el voltaje de salida $ V_ {0} $ del circuito anterior usando superposition theorem usando los siguientes pasos -
Paso 1
En primer lugar, calculemos el voltaje de salida $ V_ {01} $ considerando solo $ V_ {1} $.
Para ello, elimine $ V_ {2} $ haciéndolo cortocircuito. Entonces obtenemos elmodified circuit diagram como se muestra en la siguiente figura -

Ahora, usando el voltage division principle, calcule el voltaje en el terminal de entrada no inversora del amplificador operacional.
$$ => V_ {p} = V_ {1} \ izquierda (\ frac {R_3} {R_2 + R_3} \ derecha) $$
Ahora, el circuito anterior parece un amplificador no inversor con voltaje de entrada $ V_ {p} $. Por lo tanto, el voltaje de salida $ V_ {01} $ del circuito anterior será
$$ V_ {01} = V_ {p} \ left (1+ \ frac {R_f} {R_1} \ right) $$
Sustituyendo, el valor de $ V_ {p} $ en la ecuación anterior, obtenemos el voltaje de salida $ V_ {01} $ considerando solo $ V_ {1} $, como -
$$ V_ {01} = V_ {1} \ left (\ frac {R_3} {R_2 + R_3} \ right) \ left (1+ \ frac {R_f} {R_1} \ right) $$
Paso 2
En este paso, busquemos el voltaje de salida, $ V_ {02} $ considerando solo $ V_ {2} $. Similar a eso en el paso anterior, elimine $ V_ {1} $ haciéndolo cortocircuito. losmodified circuit diagram se muestra en la siguiente figura.

Puede observar que el voltaje en el terminal de entrada no inversora del amplificador operacional será cero voltios. Significa que el circuito anterior es simplemente uninverting op-amp. Por lo tanto, el voltaje de salida $ V_ {02} $ del circuito anterior será -
$$ V_ {02} = \ left (- \ frac {R_f} {R_1} \ right) V_ {2} $$
Paso 3
En este paso, obtendremos el voltaje de salida $ V_ {0} $ del circuito sustractor por adding the output voltagesobtenido en Step1 y Step2. Matemáticamente, se puede escribir como
$$ V_ {0} = V_ {01} + V_ {02} $$
Sustituyendo los valores de $ V_ {01} $ y $ V_ {02} $ en la ecuación anterior, obtenemos -
$$ V_ {0} = V_ {1} \ left (\ frac {R_3} {R_2 + R_3} \ right) \ left (1+ \ frac {R_f} {R_1} \ right) + \ left (- \ frac {R_f} {R_1} \ right) V_ {2} $$
$$ => V_ {0} = V_ {1} \ izquierda (\ frac {R_3} {R_2 + R_3} \ derecha) \ izquierda (1+ \ frac {R_f} {R_1} \ derecha) - \ izquierda (\ frac {R_f} {R_1} \ right) V_ {2} $$
Si $ R_ {f} = R_ {1} = R_ {2} = R_ {3} = R $, entonces el voltaje de salida $ V_ {0} $ será
$$ V_ {0} = V_ {1} \ left (\ frac {R} {R + R} \ right) \ left (1+ \ frac {R} {R} \ right) - \ left (\ frac { R} {R} \ derecha) V_ {2} $$
$$ => V_ {0} = V_ {1} \ izquierda (\ frac {R} {2R} \ derecha) (2) - (1) V_ {2} $$
$$ V_ {0} = V_ {1} -V_ {2} $$
Por lo tanto, el circuito sustractor basado en amplificador operacional discutido anteriormente producirá una salida, que es la diferencia de dos voltajes de entrada $ V_ {1} $ y $ V_ {2} $, cuando todas las resistencias presentes en el circuito tienen el mismo valor .