Osciladores sinusoidales
Un oscilador es un circuito electrónico que produce una señal periódica. Si el oscilador produce oscilaciones sinusoidales, se denomina comosinusoidal oscillator. Convierte la energía de entrada de una fuente de CC en una energía de salida de CA de una señal periódica. Esta señal periódica tendrá una frecuencia y amplitud específicas.
los block diagram de un oscilador sinusoidal se muestra en la siguiente figura:
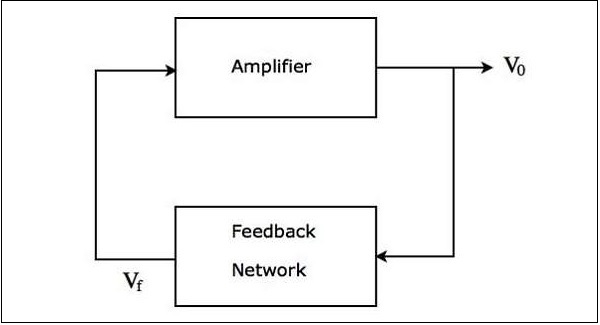
La figura anterior consiste principalmente en two blocks: un amplificador y una red de retroalimentación. La red de retroalimentación toma una parte de la salida del amplificador como entrada y produce una señal de voltaje. Esta señal de voltaje se aplica como entrada al amplificador.
El diagrama de bloques de un oscilador sinusoidal que se muestra arriba produce oscilaciones sinusoidales, cuando lo siguiente two conditions están satisfechos -
los loop gain $ A_ {v} \ beta $ del diagrama de bloques anterior del oscilador sinusoidal debe ser mayor o igual a unity. Aquí, $ A_ {v} $ y $ \ beta $ son la ganancia del amplificador y la ganancia de la red de retroalimentación, respectivamente.
El total phase shift alrededor del bucle del diagrama de bloques anterior de un oscilador sinusoidal debe ser 00 o 3600.
Las dos condiciones anteriores juntas se denominan como Barkhausen criteria.
Osciladores basados en amplificador operacional
Existen two tipos de osciladores basados en amplificadores operacionales.
- Oscilador de cambio de fase RC
- Oscilador de puente de Viena
Esta sección analiza cada uno de ellos en detalle.
Oscilador de cambio de fase RC
El oscilador basado en amplificador operacional, que produce una señal de voltaje sinusoidal en la salida con la ayuda de un amplificador inversor y una red de retroalimentación, se conoce como RC phase shift oscillator. Esta red de retroalimentación consta de tres secciones RC en cascada.
los circuit diagram de un oscilador de cambio de fase RC se muestra en la siguiente figura:
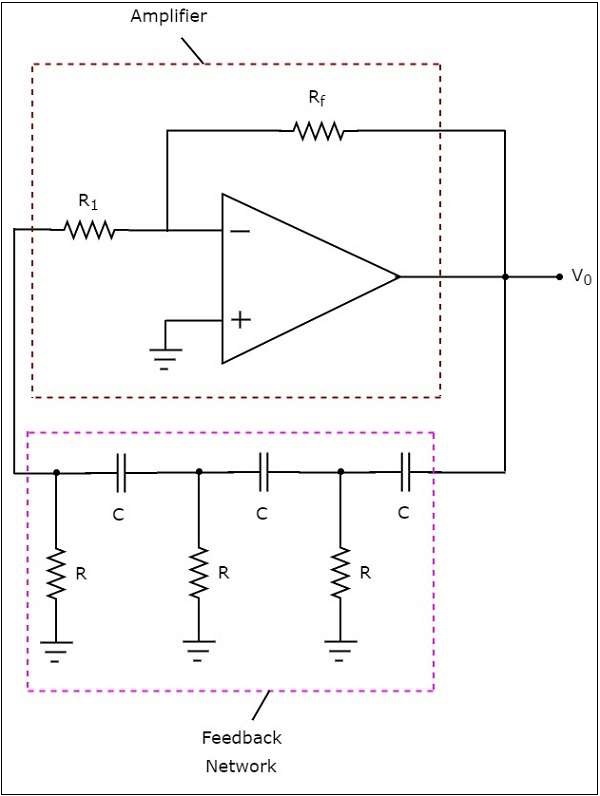
En el circuito anterior, el amplificador operacional está operando en inverting mode. Por tanto, proporciona un cambio de fase de 180 0 . La red de retroalimentación presente en el circuito anterior también proporciona un cambio de fase de 180 0 , ya que cada sección RC proporciona un cambio de fase de 60 0 . Por lo tanto, el circuito anterior proporciona un cambio de fase total de 360 0 a alguna frecuencia.
los output frequency de un oscilador de cambio de fase RC es -
$$ f = \ frac {1} {2 \ Pi RC \ sqrt [] {6}} $$
los gain $A_{v}$ de un amplificador inversor debe ser mayor o igual a -29,
$$ es decir, - \ frac {R_f} {R_1} \ geq-29 $$
$$ => \ frac {R_f} {R_1} \ geq-29 $$
$$ => R_ {f} \ geq29R_ {1} $$
Por tanto, debemos considerar el valor de la resistencia de retroalimentación $ R_ {f} $, como mínimo 29 veces el valor de la resistencia $ R_ {1} $, para producir oscilaciones sostenidas en la salida de un oscilador de cambio de fase RC.
Oscilador del puente de Viena
El oscilador basado en amplificador operacional, que produce una señal de voltaje sinusoidal en la salida con la ayuda de un amplificador no inversor y una red de retroalimentación, se conoce como Wien bridge oscillator.
los circuit diagram de un oscilador de puente de Wien se muestra en la siguiente figura:
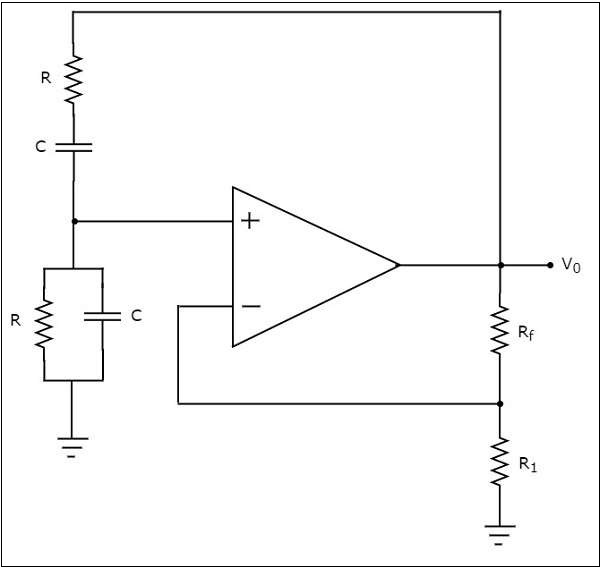
En el circuito que se muestra arriba para el oscilador de puente Wein, el amplificador operacional está operando en non inverting mode. Por tanto, proporciona un desplazamiento de fase de 00. Por tanto, la red de retroalimentación presente en el circuito anterior no debería proporcionar ningún desplazamiento de fase.
Si la red de retroalimentación proporciona algún cambio de fase, entonces tenemos que balance the bridgede tal manera que no debería haber ningún cambio de fase. Entonces, el circuito anterior proporciona un cambio de fase total de 0 0 a alguna frecuencia.
los output frequency del oscilador de puente de Viena es
$$ f = \ frac {1} {2 \ Pi RC} $$
los gain $A_{v}$ del amplificador no inversor debe ser mayor o igual a 3
$$ es decir, 1 + \ frac {R_f} {R_1} \ geq3 $$
$$ => \ frac {R_f} {R_1} \ geq2 $$
$$ => R_ {f} \ geq2R_ {1} $$
Entonces, deberíamos considerar el valor de la resistencia de retroalimentación $ R_ {f} $ al menos dos veces el valor de la resistencia, $ R_ {1} $ para producir oscilaciones sostenidas en la salida del oscilador de puente de Wien.