Amplificadores de registro y anti-registro
Los circuitos electrónicos que realizan las operaciones matemáticas como logaritmo y antilogaritmo (exponencial) con una amplificación se denominan como Logarithmic amplifier y Anti-Logarithmic amplifier respectivamente.
Este capítulo trata sobre la Logarithmic amplifier y Anti-Logarithmic amplifieren detalle. Tenga en cuenta que estos amplificadores se incluyen en aplicaciones no lineales.
Amplificador logarítmico
UN logarithmic amplifiero un log amplifier, es un circuito electrónico que produce una salida que es proporcional al logaritmo de la entrada aplicada. Esta sección trata en detalle sobre el amplificador logarítmico basado en amplificador operacional.
Un amplificador logarítmico basado en amplificador operacional produce un voltaje en la salida, que es proporcional al logaritmo del voltaje aplicado a la resistencia conectada a su terminal inversora. loscircuit diagram de un amplificador logarítmico basado en amplificador operacional se muestra en la siguiente figura:
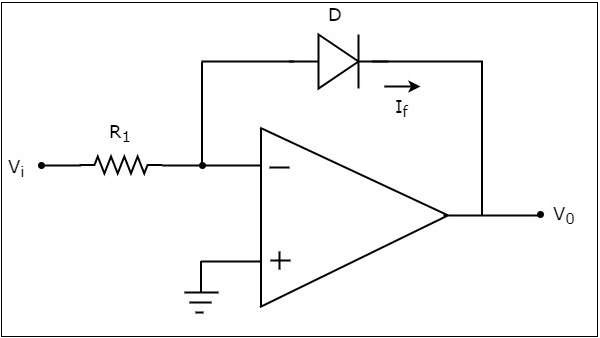
En el circuito anterior, el terminal de entrada no inversora del amplificador operacional está conectado a tierra. Eso significa que se aplica cero voltios en el terminal de entrada no inversora del amplificador operacional.
De acuerdo con la virtual short concept, el voltaje en el terminal de entrada inversora de un amplificador operacional será igual al voltaje en su terminal de entrada no inversora. Entonces, el voltaje en el terminal de entrada inversora será cero voltios.
los nodal equation en el nodo de la terminal de entrada inversora es -
$$ \ frac {0-V_i} {R_1} + I_ {f} = 0 $$
$$ => I_ {f} = \ frac {V_i} {R_1} ...... Ecuación 1 $$
El siguiente es el equation for current fluyendo a través de un diodo, cuando está en polarización directa -
$$ I_ {f} = I_ {s} e ^ {(\ frac {V_f} {nV_T})} ...... Ecuación 2 $$
dónde,
$ I_ {s} $ es la corriente de saturación del diodo,
$ V_ {f} $ es la caída de voltaje a través del diodo, cuando está en polarización directa,
$ V_ {T} $ es el voltaje térmico equivalente del diodo.
los KVL equation alrededor del circuito de retroalimentación del amplificador operacional será:
$$ 0-V_ {f} -V_ {0} = 0 $$
$$ => V_ {f} = - V_ {0} $$
Sustituyendo el valor de $ V_ {f} $ en la Ecuación 2, obtenemos -
$$ I_ {f} = I_ {s} e ^ {\ left (\ frac {-V_0} {nV_T} \ right)} ...... Ecuación 3 $$
Observe que los términos del lado izquierdo de la ecuación 1 y la ecuación 3 son iguales. Por lo tanto, iguale el término del lado derecho de esas dos ecuaciones como se muestra a continuación:
$$ \ frac {V_i} {R_1} = I_ {s} e ^ {\ left (\ frac {-V_0} {nV_T} \ right)} $$
$$ \ frac {V_i} {R_1I_s} = e ^ {\ left (\ frac {-V_0} {nV_T} \ right)} $$
Aplicando natural logarithm en ambos lados, obtenemos -
$$ In \ left (\ frac {V_i} {R_1I_s} \ right) = \ frac {-V_0} {nV_T} $$
$$ V_ {0} = - {nV_T} En \ left (\ frac {V_i} {R_1I_s} \ right) $$
Tenga en cuenta que en la ecuación anterior, los parámetros n, $ {V_T} $ y $ I_ {s} $ son constantes. Entonces, el voltaje de salida $ V_ {0} $ será proporcional alnatural logarithm del voltaje de entrada $ V_ {i} $ para un valor fijo de resistencia $ R_ {1} $.
Por lo tanto, el circuito amplificador logarítmico basado en amplificador operacional discutido anteriormente producirá una salida, que es proporcional al logaritmo natural del voltaje de entrada $ {V_T} $, cuando $ {R_1I_s} = 1V $.
Observe que el voltaje de salida $ V_ {0} $ tiene un negative sign, que indica que existe una diferencia de fase de 180 0 entre la entrada y la salida.
Amplificador antilogarítmico
Un anti-logarithmic amplifier, o un anti-log amplifier, es un circuito electrónico que produce una salida que es proporcional al antilogaritmo de la entrada aplicada. Esta sección analiza en detalle el amplificador antilogarítmico basado en amplificador operacional.
Un amplificador antilogarítmico basado en amplificador operacional produce un voltaje en la salida, que es proporcional al antilogaritmo del voltaje que se aplica al diodo conectado a su terminal inversor.
los circuit diagram de un amplificador antilogarítmico basado en amplificador operacional se muestra en la siguiente figura:

En el circuito que se muestra arriba, el terminal de entrada no inversora del amplificador operacional está conectado a tierra. Significa que se aplica cero voltios a su terminal de entrada no inversora.
De acuerdo con la virtual short concept, el voltaje en el terminal de entrada inversora del amplificador operacional será igual al voltaje presente en su terminal de entrada no inversora. Entonces, el voltaje en su terminal de entrada inversora será cero voltios.
los nodal equation en el nodo de la terminal de entrada inversora es -
$$ - I_ {f} + \ frac {0-V_0} {R_f} = 0 $$
$$ => - \ frac {V_0} {R_f} = I_ {f} $$
$$ => V_ {0} = - R_ {f} I_ {f} ......... Ecuación 4 $$
Sabemos que la ecuación para la corriente que fluye a través de un diodo, cuando está en polarización directa, es la siguiente:
$$ I_ {f} = I_ {s} e ^ {\ left (\ frac {V_f} {nV_T} \ right)} $$
Sustituyendo el valor de $ I_ {f} $ en la Ecuación 4, obtenemos
$$ V_ {0} = - R_ {f} \ left \ {{I_ {s} e ^ {\ left (\ frac {V_f} {nV_T} \ right)}} \ right \} $$
$$ V_ {0} = - R_ {f} {I_ {s} e ^ {\ left (\ frac {V_f} {nV_T} \ right)}} ...... Ecuación 5 $$
La ecuación KVL en el lado de entrada del terminal inversor del amplificador operacional será
$$ V_ {i} -V_ {f} = 0 $$
$$ V_ {f} = V_ {i} $$
Sustituyendo, el valor de en la Ecuación 5, obtenemos -
$$ V_ {0} = - R_ {f} {I_ {s} e ^ {\ left (\ frac {V_i} {nV_T} \ right)}} $$
Tenga en cuenta que, en la ecuación anterior, los parámetros n, $ {V_T} $ y $ I_ {s} $ son constantes. Entonces, el voltaje de salida $ {V_0} $ será proporcional alanti-natural logarithm (exponencial) del voltaje de entrada $ {V_i} $, para un valor fijo de resistencia de retroalimentación $ {R_f} $.
Por lo tanto, el circuito amplificador antilogarítmico basado en amplificador operacional discutido anteriormente producirá una salida, que es proporcional al logaritmo antinatural (exponencial) del voltaje de entrada $ {V_i} $ cuando, $ {R_fI_s} = 1V $. Observe que el voltaje de salida $ {V_0} $ tiene unnegative sign, que indica que existe una diferencia de fase de 180 0 entre la entrada y la salida.