Volume d'un solide constitué de cubes avec des longueurs d'arête de fraction unitaire
Ici, nous trouvons le volume de solides constitués de cubes avec des longueurs d'arête de fraction unitaire. Considérons par exemple un solide de dimensions 3 en × 3 en × 3 fait de petits cubes avec des longueurs d'arête $ \ frac {1} {2} $ pouces.
Dans ce cas, le solide est constitué de 6 × 6 × 6 petits cubes de longueur d'arête $ \ frac {1} {2} $ pouces. Donc, le volume du solide dans ce cas serait
Volume = lwh = 6 $ \ fois \ frac {1} {2} \ fois 6 \ fois \ frac {1} {2} \ fois 6 \ fois \ frac {1} {2} $
= 3 × 3 × 3 = 27 pouces cubes
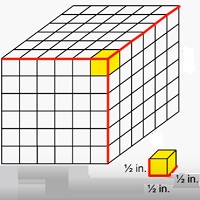
Formule pour le volume de solide constitué de cubes avec des longueurs de bord fractionnaires unitaires
En supposant que le solide est un cube d'arête a unités
b = nombre de cubes avec une longueur de bord fractionnaire unitaire le long de chaque bord
k = longueur de bord fractionnaire unitaire
Volume of solid = b × k × b × k × b × k cubic units
Trouvez le volume du solide suivant de cubes avec des longueurs d'arête de fraction unitaire. Chaque unité de prismes est mesurée en cm (pas à l'échelle)
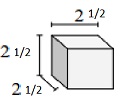
Solution
Step 1:
Solide de cubes avec une longueur d'arête de fraction unitaire de $ \ frac {1} {2} $ cm
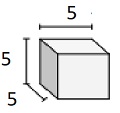
Step 2:
Volume V = lwh = $ 2 \ frac {1} {2} \ times 2 \ frac {1} {2} \ times 2 \ frac {1} {2} $
= 5 $ \ fois \ frac {1} {2} \ fois 5 \ fois \ frac {1} {2} \ fois 5 \ fois \ frac {1} {2} $
= 15 $ \ frac {5} {8} $ cu cm
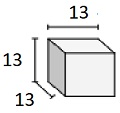
Trouvez le volume du solide suivant de cubes avec des longueurs d'arête de fraction unitaire. Chaque unité de prismes est mesurée en cm (pas à l'échelle)
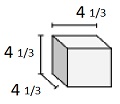
Solution
Step 1:
Solide de cubes avec une longueur d'arête de fraction unitaire de $ \ frac {1} {3} $ cm
Step 2:
Volume V = lwh = 4 $ \ frac {1} {3} \ fois 4 \ frac {1} {3} \ fois 4 \ frac {1} {3} $
= 13 $ \ fois \ frac {1} {3} \ fois 13 \ fois \ frac {1} {3} \ fois 13 \ fois \ frac {1} {3} $
= 81 $ \ frac {10} {27} $ cu cm