MATLAB - Graphiques

Ce chapitre continuera à explorer les capacités de traçage et graphiques de MATLAB. Nous discuterons -

Dessiner des graphiques à barres
Dessiner des contours
Tracés en trois dimensions

Dessin de graphiques à barres

le barcommande dessine un histogramme à deux dimensions. Prenons un exemple pour démontrer l'idée.

Exemple

Ayons une classe imaginaire avec 10 élèves. Nous savons que le pourcentage de notes obtenues par ces élèves est de 75, 58, 90, 87, 50, 85, 92, 75, 60 et 95. Nous allons dessiner le diagramme à barres pour ces données.

Créez un fichier de script et tapez le code suivant -

x = [1:10];
y = [75, 58, 90, 87, 50, 85, 92, 75, 60, 95];
bar(x,y), xlabel('Student'),ylabel('Score'),
title('First Sem:')
print -deps graph.eps

Lorsque vous exécutez le fichier, MATLAB affiche le graphique à barres suivant -

Dessiner des contours

Une ligne de contour d'une fonction de deux variables est une courbe le long de laquelle la fonction a une valeur constante. Les lignes de contour sont utilisées pour créer des cartes de contour en joignant des points d'égale élévation au-dessus d'un niveau donné, tel que le niveau moyen de la mer.

MATLAB fournit un contour fonction pour dessiner des cartes de contour.

Exemple

Générons une carte de contour qui montre les courbes de niveau pour une fonction donnée g = f (x, y). Cette fonction a deux variables. Nous devrons donc générer deux variables indépendantes, c'est-à-dire deux ensembles de données x et y. Cela se fait en appelant lemeshgrid commander.

le meshgrid La commande est utilisée pour générer une matrice d'éléments qui donnent la plage sur x et y avec la spécification d'incrément dans chaque cas.

Tracons notre fonction g = f (x, y), où −5 ≤ x ≤ 5, −3 ≤ y ≤ 3. Prenons un incrément de 0,1 pour les deux valeurs. Les variables sont définies comme -

[x,y] = meshgrid(–5:0.1:5, –3:0.1:3);

Enfin, nous devons attribuer la fonction. Soit notre fonction: x ² + y ²

Créez un fichier de script et tapez le code suivant -

[x,y] = meshgrid(-5:0.1:5,-3:0.1:3);   %independent variables
g = x.^2 + y.^2;                       % our function
contour(x,y,g)                         % call the contour function
print -deps graph.eps

Lorsque vous exécutez le fichier, MATLAB affiche la carte de contour suivante -

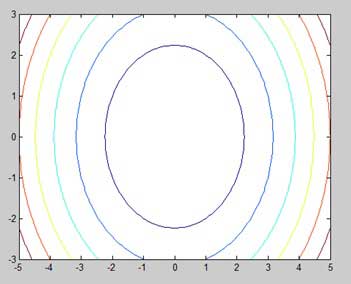
Modifions un peu le code pour embellir la carte

[x,y] = meshgrid(-5:0.1:5,-3:0.1:3);   %independent variables
g = x.^2 + y.^2;                       % our function
[C, h] = contour(x,y,g);               % call the contour function
set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2)
print -deps graph.eps

Lorsque vous exécutez le fichier, MATLAB affiche la carte de contour suivante -

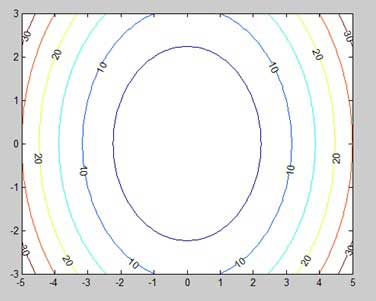
Tracés tridimensionnels

Les graphiques en trois dimensions affichent essentiellement une surface définie par une fonction en deux variables, g = f (x, y).

Comme précédemment, pour définir g, nous créons d'abord un ensemble de (x, y) points sur le domaine de la fonction en utilisant le meshgridcommander. Ensuite, nous attribuons la fonction elle-même. Enfin, nous utilisons lesurf commande pour créer un tracé de surface.

L'exemple suivant illustre le concept -

Exemple

Créons une carte de surface 3D pour la fonction g = xe ^{- (x ² + y ² )}

Créez un fichier de script et tapez le code suivant -

[x,y] = meshgrid(-2:.2:2);
g = x .* exp(-x.^2 - y.^2);
surf(x, y, g)
print -deps graph.eps

Lorsque vous exécutez le fichier, MATLAB affiche la carte 3D suivante -

Vous pouvez également utiliser le meshcommande pour générer une surface tridimensionnelle. Cependant, lesurf La commande affiche à la fois les lignes de connexion et les faces de la surface en couleur, tandis que la commande mesh La commande crée une surface filaire avec des lignes colorées reliant les points de définition.