MATLAB - Polynômes
MATLAB représente les polynômes sous forme de vecteurs lignes contenant des coefficients classés par puissances décroissantes. Par exemple, l'équation P (x) = x 4 + 7x 3 - 5x + 9 pourrait être représentée par -
p = [1 7 0 -5 9];
Évaluation des polynômes
le polyvalLa fonction est utilisée pour évaluer un polynôme à une valeur spécifiée. Par exemple, pour évaluer notre polynôme précédentp, à x = 4, tapez -
p = [1 7 0 -5 9];
polyval(p,4)MATLAB exécute les instructions ci-dessus et renvoie le résultat suivant -
ans = 693MATLAB fournit également le polyvalmfonction d'évaluation d'un polynôme matriciel. Un polynôme matriciel est unpolynomial avec des matrices comme variables.
Par exemple, créons une matrice carrée X et évaluons le polynôme p, en X -
p = [1 7 0 -5 9];
X = [1 2 -3 4; 2 -5 6 3; 3 1 0 2; 5 -7 3 8];
polyvalm(p, X)MATLAB exécute les instructions ci-dessus et renvoie le résultat suivant -
ans =
2307 -1769 -939 4499
2314 -2376 -249 4695
2256 -1892 -549 4310
4570 -4532 -1062 9269Trouver les racines des polynômes
le rootsLa fonction calcule les racines d'un polynôme. Par exemple, pour calculer les racines de notre polynôme p, tapez -
p = [1 7 0 -5 9];
r = roots(p)MATLAB exécute les instructions ci-dessus et renvoie le résultat suivant -
r =
-6.8661 + 0.0000i
-1.4247 + 0.0000i
0.6454 + 0.7095i
0.6454 - 0.7095iLa fonction polyest un inverse de la fonction racines et renvoie aux coefficients polynomiaux. Par exemple -
p2 = poly(r)MATLAB exécute les instructions ci-dessus et renvoie le résultat suivant -
p2 =
Columns 1 through 3:
1.00000 + 0.00000i 7.00000 + 0.00000i 0.00000 + 0.00000i
Columns 4 and 5:
-5.00000 - 0.00000i 9.00000 + 0.00000iAjustement de courbe polynomiale
le polyfitLa fonction trouve les coefficients d'un polynôme qui correspond à un ensemble de données au sens des moindres carrés. Si x et y sont deux vecteurs contenant les données x et y à ajuster sur un polynôme à n degrés, alors nous obtenons le polynôme ajustant les données en écrivant -
p = polyfit(x,y,n)Exemple
Créez un fichier de script et tapez le code suivant -
x = [1 2 3 4 5 6]; y = [5.5 43.1 128 290.7 498.4 978.67]; %data
p = polyfit(x,y,4) %get the polynomial
% Compute the values of the polyfit estimate over a finer range,
% and plot the estimate over the real data values for comparison:
x2 = 1:.1:6;
y2 = polyval(p,x2);
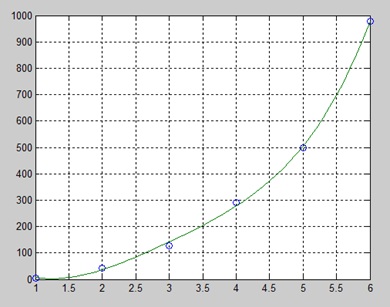
plot(x,y,'o',x2,y2)
grid onLorsque vous exécutez le fichier, MATLAB affiche le résultat suivant -
p =
4.1056 -47.9607 222.2598 -362.7453 191.1250Et trace le graphique suivant -