MATLAB - Opérateurs

Un opérateur est un symbole qui indique au compilateur d'effectuer des manipulations mathématiques ou logiques spécifiques. MATLAB est conçu pour fonctionner principalement sur des matrices et des tableaux entiers. Par conséquent, les opérateurs de MATLAB fonctionnent à la fois sur des données scalaires et non scalaires. MATLAB permet les types d'opérations élémentaires suivants -

Opérateurs arithmétiques
Opérateurs relationnels
Opérateurs logiques
Opérations au niveau du bit
Définir les opérations

Opérateurs arithmétiques

MATLAB permet deux types différents d'opérations arithmétiques -

Opérations arithmétiques matricielles
Opérations arithmétiques de tableau

Les opérations arithmétiques matricielles sont les mêmes que celles définies en algèbre linéaire. Les opérations de tableau sont exécutées élément par élément, à la fois sur un tableau unidimensionnel et multidimensionnel.

Les opérateurs de matrice et les opérateurs de tableau sont différenciés par le symbole point (.). Cependant, comme l'opération d'addition et de soustraction est la même pour les matrices et les tableaux, l'opérateur est le même dans les deux cas. Le tableau suivant donne une brève description des opérateurs -

Afficher des exemples

N ° Sr.	Opérateur et description
1	+ Addition ou plus unaire. A + B ajoute les valeurs stockées dans les variables A et B. A et B doivent avoir la même taille, sauf si l'une est un scalaire. Un scalaire peut être ajouté à une matrice de n'importe quelle taille.
2	- Soustraction ou moins unaire. AB soustrait la valeur de B de A. A et B doivent avoir la même taille, sauf si l'un est un scalaire. Un scalaire peut être soustrait d'une matrice de n'importe quelle taille.
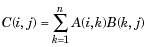
3	* Multiplication matricielle. C = A * B est le produit algébrique linéaire des matrices A et B. Plus précisément, Pour A et B non scalaires, le nombre de colonnes de A doit être égal au nombre de lignes de B. Un scalaire peut multiplier une matrice de n'importe quelle taille.
4	.* Multiplication de tableau. A. * B est le produit élément par élément des tableaux A et B. A et B doivent avoir la même taille, sauf si l'un d'entre eux est un scalaire.
5	/ Division droite par barre oblique ou matrice. B / A est à peu près le même que B * inv (A). Plus précisément, B / A = (A '\ B') '.
6	./ Division droite du tableau. A./B est la matrice avec les éléments A (i, j) / B (i, j). A et B doivent avoir la même taille, sauf si l'un d'eux est un scalaire.
sept	\ Antislash ou division gauche matricielle. Si A est une matrice carrée, A \ B est à peu près le même que inv (A) * B, sauf qu'il est calculé d'une manière différente. Si A est une matrice n par n et B est un vecteur colonne à n composantes, ou une matrice à plusieurs de ces colonnes, alors X = A \ B est une solution à l'équation AX = B . Un message d'avertissement s'affiche si A est mal mis à l'échelle ou presque singulier.
8	.\ Division du tableau à gauche. A. \ B est la matrice avec les éléments B (i, j) / A (i, j). A et B doivent avoir la même taille, sauf si l'un d'eux est un scalaire.
9	^ Puissance de la matrice. X ^ p est X à la puissance p, si p est un scalaire. Si p est un entier, la puissance est calculée par quadrillage répété. Si l'entier est négatif, X est inversé en premier. Pour les autres valeurs de p, le calcul fait intervenir des valeurs propres et des vecteurs propres, tels que si [V, D] = eig (X), alors X ^ p = V * D. ^ p / V.
dix	.^ Puissance de la baie. A. ^ B est la matrice avec les éléments A (i, j) à la puissance B (i, j). A et B doivent avoir la même taille, sauf si l'un d'eux est un scalaire.
11	' Matrice transposée. A 'est la transposée algébrique linéaire de A. Pour les matrices complexes, c'est la transposée conjuguée complexe.
12	.' Transposer le tableau. UNE.' est le tableau transposé de A. Pour les matrices complexes, cela n'implique pas de conjugaison.

Opérateurs relationnels

Les opérateurs relationnels peuvent également travailler sur des données scalaires et non scalaires. Les opérateurs relationnels des tableaux effectuent des comparaisons élément par élément entre deux tableaux et renvoient un tableau logique de la même taille, avec des éléments définis sur 1 logique (vrai) où la relation est vraie et les éléments définis sur 0 logique (faux) là où elle est ne pas.

Le tableau suivant présente les opérateurs relationnels disponibles dans MATLAB -

Afficher des exemples

N ° Sr.	Opérateur et description
1	< Moins que
2	<= Inférieur ou égal à
3	> Plus grand que
4	>= Plus grand ou égal à
5	== Égal à
6	~= Pas égal à

Opérateurs logiques

MATLAB propose deux types d'opérateurs et de fonctions logiques -

Élément par élément - Ces opérateurs opèrent sur les éléments correspondants des tableaux logiques.
Court-circuit - Ces opérateurs fonctionnent sur des expressions scalaires et logiques.

Les opérateurs logiques élément par élément opèrent élément par élément sur des tableaux logiques. Les symboles &, | et ~ sont les opérateurs de tableau logique AND, OR et NOT.

Les opérateurs logiques de court-circuit permettent le court-circuit sur les opérations logiques. Les symboles && et || sont les opérateurs logiques de court-circuit ET et OU.

Afficher des exemples

Opérations au niveau du bit

Les opérateurs au niveau du bit travaillent sur les bits et effectuent des opérations bit par bit. Les tables de vérité pour &, | et ^ sont les suivantes:

p	q	p & q	p \| q	p ^ q
0	0	0	0	0
0	1	0	1	1
1	1	1	1	0
1	0	0	1	1

Supposons que A = 60; et B = 13; Maintenant au format binaire, ils seront comme suit -

A = 0011 1100

B = 0000 1101

-----------------

A&B = 0000 1100

A | B = 0011 1101

A ^ B = 0011 0001

~ A = 1100 0011

MATLAB fournit diverses fonctions pour les opérations bit par bit comme les opérations 'bitwise et', 'bitwise ou' et 'bitwise not', les opérations de décalage, etc.

Le tableau suivant montre les opérations binaires couramment utilisées -

Afficher des exemples

Fonction	Objectif
bitand (a, b)	ET bit par bit des entiers a et b
bitcmp (a)	Complément bit par bit d' un
bitget (a, pos)	Obtenir le bit à la position spécifiée pos , dans le tableau d'entiers a
bitor (a, b)	OU bit par bit des entiers a et b
jeu de bits (a, pos)	Définir le bit à l'emplacement spécifique pos d' un
décalage de bits (a, k)	Renvoie un décalage vers la gauche de k bits, ce qui équivaut à multiplier par 2 ^k . Les valeurs négatives de k correspondent au décalage des bits vers la droite ou à la division par 2 ^{\| k \|}et arrondir à l'entier le plus proche vers l'infini négatif. Tous les bits de débordement sont tronqués.
bitxor (a, b)	XOR bit par bit des entiers a et b
swapbytes	Ordre des octets de permutation

Définir les opérations

MATLAB fournit diverses fonctions pour les opérations d'ensemble, comme l'union, l'intersection et le test de l'appartenance à l'ensemble, etc.

Le tableau suivant présente certaines opérations de set couramment utilisées -

Afficher des exemples

N ° Sr.	Description de la fonction
1	intersect(A,B) Définir l'intersection de deux tableaux; renvoie les valeurs communes à A et B. Les valeurs renvoyées sont dans l'ordre trié.
2	intersect(A,B,'rows') Traite chaque ligne de A et chaque ligne de B comme des entités uniques et renvoie les lignes communes à A et B. Les lignes de la matrice renvoyée sont triées.
3	ismember(A,B) Renvoie un tableau de la même taille que A, contenant 1 (vrai) où les éléments de A se trouvent dans B. Ailleurs, il renvoie 0 (faux).
4	ismember(A,B,'rows') Traite chaque ligne de A et chaque ligne de B comme des entités uniques et renvoie un vecteur contenant 1 (vrai) où les lignes de la matrice A sont également des lignes de B. Ailleurs, il renvoie 0 (faux).
5	issorted(A) Renvoie 1 logique (vrai) si les éléments de A sont triés et 0 logique (faux) dans le cas contraire. L'entrée A peut être un vecteur ou un tableau de cellules N-par-1 ou 1-par-N de chaînes.A is considered to be sorted if A et la sortie de tri (A) sont égales.
6	issorted(A, 'rows') Renvoie 1 logique (vrai) si les lignes de la matrice bidimensionnelle A sont triées, et 0 logique (faux) dans le cas contraire. Matrix A is considered to be sorted if A et la sortie des sortrows (A) sont égales.
sept	setdiff(A,B) Définit la différence de deux tableaux; renvoie les valeurs de A qui ne sont pas de B. Les valeurs du tableau renvoyé sont triées.
8	setdiff(A,B,'rows') Traite chaque ligne de A et chaque ligne de B comme des entités uniques et renvoie les lignes de A qui ne sont pas dans B. Les lignes de la matrice retournée sont triées. L'option 'rows' ne prend pas en charge les tableaux de cellules.
9	setxor Définit le OU exclusif de deux tableaux
dix	union Définit l'union de deux tableaux
11	unique Valeurs uniques dans le tableau