Recherche de l'aire d'un triangle rectangle ou de son rectangle correspondant

introduction

Area of a right triangle

Considérons un rectangle de longueur l unités et de largeur w unités. Trouvons une diagonale et découpons le rectangle. Découpons également le long de la diagonale pour former deux triangles rectangles.

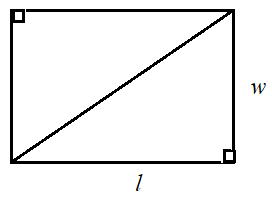
On constate que les deux triangles rectangles ont la même taille et la même aire et sont congruents. Ainsi, l'aire de chaque triangle rectangle est la moitié de l'aire du rectangle.

Aire du triangle rectangle = $ \ frac {1} {2} $ aire du rectangle = $ \ frac {1} {2} $ l × w

La longueur l du rectangle est la base b du triangle rectangle et la largeur w du rectangle est la hauteur h du triangle rectangle.

So area of right triangle = $\mathbf{\frac{1}{2}}$ l × w = $\mathbf{\frac{1}{2}}$ b × h

L'aire d'un triangle rectangle est la moitié de l'aire de son rectangle correspondant

Exemple 1:

Trouvez la zone du triangle rectangle suivant et son rectangle correspondant.

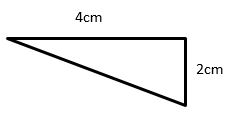
Solution

Step 1:

Aire du triangle droit = $ \ frac {1} {2} $ × b × h; b = base = 4; h = hauteur = 2

Step 2:

Aire du triangle droit = $ \ frac {1} {2} $ × 4 × 2 = 4 cm carrés

Aire du rectangle correspondant = b × h = 4 × 2 = 8 cm carrés

Exemple 2:

Trouvez la zone du triangle rectangle suivant et son rectangle correspondant.

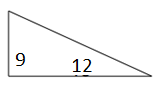
Solution

Step 1:

Aire du triangle droit = $ \ frac {1} {2} $ × b × h; b = base = 12; h = hauteur = 9

Step 2:

Aire du triangle droit = $ \ frac {1} {2} $ × 12 × 9 = 54 unités carrées

Aire du rectangle correspondant = b × h = 12 × 9 = 108 unités carrées