डीएफए न्यूनतमकरण
डीएफए मिनिमाइज़ेशन का उपयोग करके माईफिल-नेरोड प्रमेय
कलन विधि
Input - डीएफए
Output - न्यूनतम डीएफए
Step 1- सभी राज्यों की जोड़ी के लिए एक तालिका बनाएं (क्यू मैं , क्यू जे ) जरूरी नहीं कि सीधे जुड़े हों [सभी शुरू में ही अप्रकाशित हैं]
Step 2- डीएफए में प्रत्येक राज्य जोड़ी (क्यू आई , क्यू जे ) पर विचार करें जहां क्यू मैं Q एफ और क्यू जे a एफ या इसके विपरीत और उन्हें चिह्नित करता हूं। [यहाँ एफ अंतिम राज्यों का सेट है]
Step 3 - इस चरण को तब तक दोहराएं जब तक कि हम राज्यों को चिह्नित नहीं कर सकते
यदि कोई अचिह्नित युग्म (Q i , Q j ) है, तो इसे चिह्नित करें यदि जोड़ी {δ (Q i , A),, (Q i , A)} कुछ इनपुट वर्णमाला के लिए चिह्नित है।
Step 4- सभी अचिह्नित जोड़ी (Q i , Q j ) को मिलाएं और उन्हें कम DFA में एक एकल राज्य बनाएं।
उदाहरण
आइए नीचे दिखाए गए DFA को कम करने के लिए Algorithm 2 का उपयोग करें।

Step 1 - हम सभी राज्यों की जोड़ी के लिए एक तालिका बनाते हैं।
| ए | ख | सी | घ | इ | च | |
| ए | ||||||
| ख | ||||||
| सी | ||||||
| घ | ||||||
| इ | ||||||
| च |
Step 2 - हम राज्य जोड़े को चिह्नित करते हैं।
| ए | ख | सी | घ | इ | च | |
| ए | ||||||
| ख | ||||||
| सी | ✔ | ✔ | ||||
| घ | ✔ | ✔ | ||||
| इ | ✔ | ✔ | ||||
| च | ✔ | ✔ | ✔ |
Step 3- हम राज्य के जोड़े को हरे रंग के चेक मार्क के साथ, संक्रमणीय रूप से चिह्नित करने का प्रयास करेंगे। यदि हम 1 को 'a' और 'f' को स्टेट करते हैं, तो यह क्रमशः 'c' और 'f' स्टेट जाएगा। (सी, एफ) पहले से ही चिह्नित है, इसलिए हम जोड़ी (ए, एफ) को चिह्नित करेंगे। अब, हम 1 से 'b' और 'f' स्टेट का इनपुट करते हैं; यह क्रमशः 'd' और 'f' राज्य में जाएगा। (डी, एफ) पहले से ही चिह्नित है, इसलिए हम जोड़ी (बी, एफ) को चिह्नित करेंगे।
| ए | ख | सी | घ | इ | च | |
| ए | ||||||
| ख | ||||||
| सी | ✔ | ✔ | ||||
| घ | ✔ | ✔ | ||||
| इ | ✔ | ✔ | ||||
| च | ✔ | ✔ | ✔ | ✔ | ✔ |
चरण 3 के बाद, हमें राज्य संयोजन {a, b} {c, d} {c, e} {d, e} मिला है जो कि अचिह्नित हैं।
हम {c, d}, e} को {c, d}
इसलिए हमें दो संयुक्त राज्य मिले - {a, b} और {c, d, e}
इसलिए अंतिम न्यूनतम डीएफए में तीन राज्य होंगे {f}, {a, b} और {c, d, e}
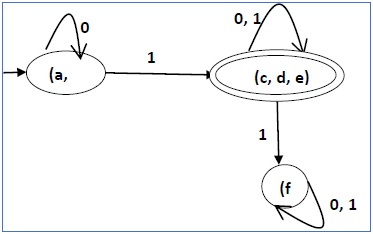
डीएफए मिनिमलाइज़ेशन इक्विवलेंस प्रमेय का उपयोग कर
यदि X और Y एक DFA में दो राज्य हैं, तो हम इन दोनों राज्यों को {X, Y} में मिला सकते हैं यदि वे अलग-अलग नहीं हैं। दो राज्य अलग-अलग हैं, यदि कम से कम एक स्ट्रिंग S है, जैसे कि X (X, S) और S (Y, S) में से एक स्वीकार कर रहा है और दूसरा स्वीकार नहीं कर रहा है। इसलिए, यदि सभी राज्य अलग-अलग हैं, तो केवल एक डीएफए न्यूनतम है।
एल्गोरिथम 3
Step 1 - सभी राज्य Q दो भागों में विभाजित हैं - final states तथा non-final states और द्वारा निरूपित किया जाता है P0। एक विभाजन में सभी राज्य 0 वें समकक्ष हैं। एक काउंटर ले लोk और इसे 0 से आरंभ करें।
Step 2- वृद्धि कश्मीर 1. द्वारा पी में प्रत्येक विभाजन के लिए कश्मीर , पी में राज्यों को विभाजित कश्मीर अगर वे k-अलग पहचानी दो विभाजन में। इस विभाजन के भीतर दो राज्य X और Y एक इनपुट होने पर k- डिफरेंशियल हैंS ऐसा है कि δ(X, S) तथा δ(Y, S) हैं (k-1) -Distinguishable।
Step 3- यदि P k k P k-1 , चरण 2 को दोहराएं, अन्यथा चरण 4 पर जाएं।
Step 4- k वें समतुल्य सेटों को मिलाएं और उन्हें कम DFA के नए राज्य बनाएं।
उदाहरण
आइए हम निम्नलिखित डीएफए पर विचार करें -

| क्ष | δ (क्यू, 0) | δ (क्यू, 1) |
|---|---|---|
| ए | ख | सी |
| ख | ए | घ |
| सी | इ | च |
| घ | इ | च |
| इ | इ | च |
| च | च | च |
हमें उपरोक्त DFA के लिए उपरोक्त एल्गोरिथ्म लागू करें -
- पी 0 = {(सी, डी, ई), (ए, बी, एफ)}
- पी 1 = {(सी, डी, ई), (ए, बी), (एफ)}
- पी 2 = {(सी, डी, ई), (ए, बी), (एफ)}
इसलिए, पी 1 = पी 2 ।
घटी हुई डीएफए में तीन राज्य हैं। निम्न डीएफए निम्नानुसार है -
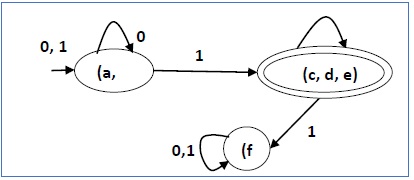
| क्यू | δ (क्यू, 0) | δ (क्यू, 1) |
|---|---|---|
| (ए, बी) | (ए, बी) | (सी, डी, ई) |
| (सी, डी, ई) | (सी, डी, ई) | (च) |
| (च) | (च) | (च) |