डिजिटल अंकगणित सर्किट
इस अध्याय में, आइए हम बाइनरी योजक और बाइनरी सबट्रैक्टर जैसे बुनियादी अंकगणितीय सर्किट के बारे में चर्चा करें। इन सर्किटों को बाइनरी मान 0 और 1 के साथ संचालित किया जा सकता है।
द्विआधारी योजक
सबसे बुनियादी अंकगणितीय ऑपरेशन इसके अतिरिक्त है। सर्किट, जो दो द्विआधारी संख्याओं को जोड़ने का कार्य करता है, के रूप में जाना जाता हैBinary adder। सबसे पहले, हम एक योजक को लागू करते हैं, जो दो बिट्स को जोड़ने का कार्य करता है।
आधा योजक
आधा योजक एक संयोजन सर्किट है, जो दो बाइनरी संख्याओं के जोड़ देता है जो ए और बी के हैं single bit। यह दो आउटपुट योग, S & carry, C का उत्पादन करता है।
Truth table आधा योजक नीचे दिखाया गया है।
| इनपुट | आउटपुट | ||
|---|---|---|---|
| ए | बी | सी | एस |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
जब हम दो बिट्स को जोड़ते हैं, तो परिणामी योग में दशमलव में 0 से 2 तक के मान हो सकते हैं। हम बाइनरी में एकल बिट के साथ दशमलव अंक 0 और 1 का प्रतिनिधित्व कर सकते हैं। लेकिन, हम द्विआधारी में सिंगल बिट के साथ दशमलव अंक 2 का प्रतिनिधित्व नहीं कर सकते। तो, हमें बाइनरी में इसका प्रतिनिधित्व करने के लिए दो बिट्स की आवश्यकता होती है।
मान लीजिए, S, S कम से कम महत्वपूर्ण बिट है और कैरी, C परिणामी राशि का सबसे महत्वपूर्ण बिट है। इनपुट, कैरी, सी के पहले तीन संयोजनों के लिए, सी शून्य है और एस के मूल्य या तो शून्य या एक के आधार पर होंगेnumber of onesइनपुट्स पर मौजूद लेकिन, इनपुट के अंतिम संयोजन के लिए, कैरी, सी एक और राशि है, एस शून्य है, क्योंकि परिणामी राशि दो है।
ट्रुथ टेबल से, हम सीधे लिख सकते हैं Boolean functions के रूप में प्रत्येक उत्पादन के लिए
$ $ S = A \ oplus B $ $
$ सी = एबी $
हम उपरोक्त कार्यों को 2-इनपुट Ex-OR गेट और 2-इनपुट और गेट के साथ कार्यान्वित कर सकते हैं। circuit diagram निम्न योजक को निम्न आकृति में दिखाया गया है।

उपरोक्त सर्किट में, एक दो इनपुट पूर्व या गेट और दो इनपुट और गेट क्रमशः योग, एस एंड कैरी, सी का उत्पादन करते हैं। इसलिए, अर्ध-योजक दो बिट्स को जोड़ने का कार्य करता है।
पूर्ण योजक
पूर्ण योजक एक संयोजन सर्किट है, जो प्रदर्शन करता है addition of three bitsए, बी और सी में । कहाँ, ए एंड बी दो समानांतर महत्वपूर्ण बिट और सी हैं में कैरी सा है, जो पिछले चरण से उत्पन्न होता है है। यह पूर्ण योजक भी दो आउटपुट योग, एस एंड कैरी, सी आउट का उत्पादन करता है , जो कि आधे योजक के समान हैं।
Truth table पूर्ण योजक के नीचे दिखाया गया है।
| इनपुट | आउटपुट | |||
|---|---|---|---|---|
| A | B | Cin | Cout | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
जब हम तीन बिट्स को जोड़ते हैं, तो परिणामी योग में दशमलव में 0 से 3 तक के मान हो सकते हैं। हम बाइनरी में एकल बिट के साथ दशमलव अंक 0 और 1 का प्रतिनिधित्व कर सकते हैं। लेकिन, हम दशमलव अंकों 2 और 3 को द्विआधारी में एकल बिट के साथ नहीं दिखा सकते हैं। तो, हमें बाइनरी में उन दो दशमलव अंकों का प्रतिनिधित्व करने के लिए दो बिट्स की आवश्यकता होती है।
मान लीजिए, सम, एस कम से कम महत्वपूर्ण है और कैरी, सी आउट परिणामी राशि का सबसे महत्वपूर्ण बिट है। सत्य तालिका में इनपुट के सभी संयोजनों के लिए आउटपुट के मूल्यों को भरना आसान है। बस गिनती हैnumber of onesइनपुट पर मौजूद है और आउटपुट पर बराबर बाइनरी नंबर लिखता है। तो सी में शून्य के बराबर है, तो पूर्ण योजक सच्चाई तालिका आधा योजक सच तालिका के समान ही है।
हम निम्नलिखित प्राप्त करेंगे Boolean functions सरलीकरण के बाद प्रत्येक आउटपुट के लिए।
$ $ S = A \ oplus B \ oplus C_ {in} $ $
$ c_ {out} = AB + \ left (A \ oplus B \ right) c_ {in} $
सम, एस एक के बराबर है, जब इनपुट पर मौजूद विषम संख्या। हम जानते हैं कि Ex-OR फाटक एक आउटपुट का उत्पादन करता है, जो एक विषम कार्य है। तो, हम या तो दो 2input पूर्व या फाटक या एक 3-इनपुट पूर्व या राशि का उत्पादन करने के लिए गेट का उपयोग कर सकते, एस हम कैरी, सी लागू कर सकते हैं बाहर दो 2input और फाटक और एक या गेट का उपयोग कर। circuit diagram पूर्ण योजक निम्न आकृति में दिखाया गया है।
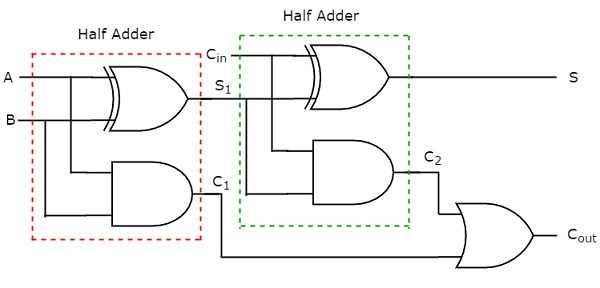
इस योजक को कहा जाता है Full adderक्योंकि एक पूर्ण योजक को लागू करने के लिए, हमें दो हाफ योजक और एक OR गेट की आवश्यकता होती है। सी हैं में शून्य है, तो पूर्ण योजक आधा योजक हो जाता है। हम इसे उपरोक्त सर्किट आरेख या पूर्ण योजक के आउटपुट के बूलियन कार्यों से आसानी से सत्यापित कर सकते हैं।
4-बिट बाइनरी एडडर
4-बिट बाइनरी योजक करता है addition of two 4-bit numbers। 4-बिट बाइनरी नंबर, $ A = A_ {3} A_ {2} A_ {1} A_ {0} $ और $ B = B_ {3} B_ {2} B_ {1} B_ {0} $। हम निम्नलिखित दो तरीकों में से एक में 4-बिट बाइनरी योजक को लागू कर सकते हैं।
तीन उच्च महत्वपूर्ण बिट्स के अलावा करने के लिए दो कम से कम महत्वपूर्ण बिट्स और तीन पूर्ण योजक करने के लिए एक आधे योजक का उपयोग करें।
एकरूपता के लिए चार पूर्ण योजक का उपयोग करें। के बाद से, प्रारंभिक कैरी सी में शून्य, पूर्ण योजक जो कम से कम महत्वपूर्ण बिट जोड़ने के लिए इस्तेमाल किया जाता है आधा योजक हो जाता है।
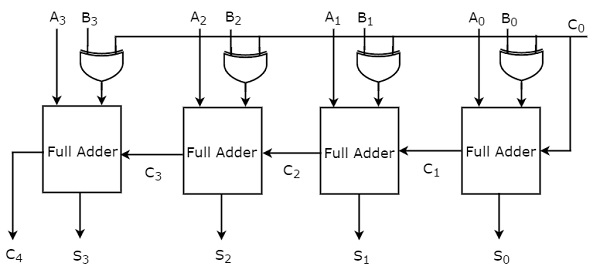
कुछ समय के लिए, हमने दूसरे दृष्टिकोण पर विचार किया। block diagram 4-बिट बाइनरी योजक को निम्न आकृति में दिखाया गया है।

यहां, 4 पूर्ण योजक कैस्केड किए जाते हैं। प्रत्येक पूर्ण योजक को दो समानांतर इनपुट ए और बी के संबंधित बिट्स मिल रहे हैं। एक पूर्ण योजक का कैरी आउटपुट बाद के उच्चतर ऑर्डर फुल एडियर का कैरी इनपुट होगा। यह 4-बिट बाइनरी योजक परिणामी राशि का उत्पादन करता है जिसमें अधिकांश 5 बिट्स होते हैं। तो, अंतिम चरण से बाहर ले जाने के लिए पूर्ण योजक MSB होगा।
इस प्रकार, हम किसी भी उच्च क्रम बाइनरी योजक को केवल पूर्ण योजक की आवश्यक संख्या को लागू करके लागू कर सकते हैं। इस बाइनरी योजक के रूप में भी कहा जाता हैripple carry (binary) adder क्योंकि कैरीप एक चरण से अगले चरण तक फैलता है।
बाइनरी सबट्रैक्टर
सर्किट, जो दो बाइनरी संख्याओं के घटाव को करता है, के रूप में जाना जाता है Binary subtractor। हम बाइनरी सबट्रैक्टर को दो तरीकों से लागू कर सकते हैं।
- कैस्केड पूर्ण सबट्रैक्टर
- 2 की पूरक विधि
पहली विधि में, हमें 'n' पूर्ण सबट्रैक्टर को कैस्केडिंग करके एक n-बिट बाइनरी सबट्रैक्टर मिलेगा। तो, पहले आप हाफ सबट्रैक्टर और फुल सबट्रैक्टर को लागू कर सकते हैं, हाफ योजक और पूर्ण योजक के समान। फिर, आप 'n' फुल सबट्रैक्टर को कैस्केडिंग करके एक n-बिट बाइनरी सबट्रैक्टर को लागू कर सकते हैं। तो, हमारे पास बाइनरी जोड़ और दो बाइनरी संख्याओं के घटाव के लिए दो अलग-अलग सर्किट होंगे।
दूसरी विधि में, हम केवल दूसरे इनपुट में कुछ संशोधन करके दो बाइनरी संख्याओं को घटाने के लिए एक ही बाइनरी योजक का उपयोग कर सकते हैं। तो, आंतरिक रूप से द्विआधारी जोड़ ऑपरेशन होता है लेकिन, आउटपुट परिणामी घटाव है।
हम जानते हैं कि दो बाइनरी नंबर A & B का घटाव इस प्रकार लिखा जा सकता है,
$ $ AB = A + \ बाएँ ({2} 's \: तारीफ \: of \: B \ right) $ $
$ \ Rightarrow AB = A + \ _ बाएँ ({1} 's \: तारीफ \: of \: B \ right) + 1 $
4-बिट बाइनरी सबट्रैक्टर
4-बिट बाइनरी सबट्रैक्टर का उत्पादन करता है subtraction of two 4-bit numbers। 4 बिट बाइनरी नंबर, $ A = A_ {3} A_ {2} A_ {1} A_ {0} $ और $ B = B_ {3} B_ {2} B_ {1} B_ {0} $। आंतरिक रूप से, 4-बिट बाइनरी सबट्रैक्टर का संचालन 4-बिट बाइनरी योजक के समान है। यदि बाइनरी नंबर ए के सामान्य बिट्स, बाइनरी नंबर बी के पूरक बिट्स और प्रारंभिक कैरी (उधार), सी के रूप में एक को 4-बिट बाइनरी योजक पर लागू किया जाता है, तो यह 4-बिट बाइनरी सबट्रैक्टर बन जाता है। block diagram 4-बिट बाइनरी सबट्रैक्टर को निम्न आकृति में दिखाया गया है।

यह 4-बिट बाइनरी सबट्रैक्टर एक आउटपुट उत्पन्न करता है, जो कि अधिकतम 5 बिट्स पर होता है। यदि बाइनरी नंबर ए बाइनरी नंबर बी से अधिक है, तो आउटपुट का एमएसबी शून्य है और शेष बिट्स एबी की परिमाण को पकड़ते हैं। यदि बाइनरी नंबर ए बाइनरी नंबर बी से कम है, तो आउटपुट का एमएसबी एक है। तो, एबी के परिमाण को प्राप्त करने के लिए आउटपुट के 2 पूरक लें।
इस प्रकार, हम किसी भी उच्च क्रम बाइनरी सबट्रैक्टर को आवश्यक संशोधनों के साथ पूर्ण योजक की आवश्यक संख्या को लागू करके लागू कर सकते हैं।
द्विआधारी योजक / घटाव
सर्किट, जिसका उपयोग किसी भी समय दो बाइनरी संख्याओं के जोड़ या घटाव के रूप में किया जा सकता है Binary Adder / subtractor। दोनों, बाइनरी योजक और बाइनरी सबट्रैक्टर में पूर्ण योजक का एक सेट होता है, जिसे कैस्केड किया जाता है। बाइनरी नंबर ए के इनपुट बिट्स सीधे बाइनरी एडिटर और बाइनरी सबट्रैक्टर दोनों में लागू होते हैं।
पूर्ण योजक के इनपुट में दो अंतर हैं जो बाइनरी योजक और बाइनरी सबट्रैक्टर में मौजूद हैं।
बाइनरी नंबर बी के इनपुट बिट्स सीधे बाइनरी एडिटर में फुल एडरों पर लागू होते हैं, जबकि बाइनरी नंबर बी के पूरक बिट्स बाइनरी सबट्रैक्टर में फुल एडरों पर लागू होते हैं।
प्रारंभिक कैरी, C 0 = 0 को 4-बिट बाइनरी योजक में लागू किया जाता है, जबकि प्रारंभिक कैरी (उधार), C 0 = 1 को 4-बिट बाइनरी सबट्रैक्टर में लागू किया जाता है।
हम जानते हैं कि ए 2-input Ex-OR gateएक आउटपुट पैदा करता है, जो पहले इनपुट के समान है जब अन्य इनपुट शून्य है। इसी तरह, यह एक आउटपुट का उत्पादन करता है, जो पहले इनपुट का पूरक होता है जब अन्य इनपुट एक होता है।
इसलिए, हम बाइनरी नंबर बी के इनपुट बिट्स को 2-इनपुट एक्स-या गेट्स पर लागू कर सकते हैं। इन सभी Ex-OR गेट्स का अन्य इनपुट C 0 है । इसलिए, सी 0 के मूल्य के आधार पर , पूर्व या द्वार द्विपदीय संख्या बी के सामान्य या पूरक बिट्स का उत्पादन करते हैं।
4-बिट बाइनरी एडडर / सबट्रैक्टर
4-बिट बाइनरी योजक / सबट्रैक्टर प्रारंभिक कैरी या उधार, 0 के मूल्य के आधार पर दो 4-बिट संख्याओं के जोड़ या घटाव का उत्पादन करता है । 4-बिट बाइनरी नंबर, $ A = A_ {3} A_ {2} A_ {1} A_ {0} $ और $ B = B_ {3} B_ {2} B_ {1} B_ {0} $। 4-बिट बाइनरी एडिटर / सबट्रैक्टर का संचालन 4-बिट बाइनरी एडिटर और 4-बिट बाइनरी सबट्रैक्टर के समान है।
बाइनरी संख्या ए और बी और प्रारंभिक कैरी या उधार, सी 0 के सामान्य बिट्स को बाहरी रूप से 4-बिट बाइनरी योजक में लागू करें। block diagram 4-बिट बाइनरी योजक / घटाव निम्न आकृति में दिखाया गया है।
यदि प्रारंभिक कैरी, 0 शून्य है, तो प्रत्येक पूर्ण योजक को बाइनरी संख्या A & B. के सामान्य बिट्स मिलते हैं, इसलिए 4-बिट बाइनरी योजक / घटाव एक आउटपुट का उत्पादन करता है, जो किaddition of two binary numbers ए और बी।
यदि प्रारंभिक उधार, 0 एक है, तो प्रत्येक पूर्ण योजक को बाइनरी नंबर ए के सामान्य बिट्स मिलते हैं और बाइनरी नंबर बी के पूरक बिट्स होते हैं। 4-बिट बाइनरी योजक / घटाव एक आउटपुट का उत्पादन करता है, जो किsubtraction of two binary numbers ए और बी।
इसलिए, अतिरिक्त पूर्व-या द्वार की सहायता से, एक ही सर्किट का उपयोग दो बाइनरी संख्याओं के जोड़ और घटाव के लिए किया जा सकता है।