डिजिटल सर्किट - K- मैप विधि
पिछले अध्यायों में, हमने बूलियन पदों और प्रमेयों का उपयोग करके बूलियन कार्यों को सरल बनाया है। यह एक समय लेने वाली प्रक्रिया है और हमें प्रत्येक चरण के बाद सरलीकृत अभिव्यक्तियों को फिर से लिखना होगा।
इस कठिनाई को दूर करने के लिए, Karnaughएक आसान तरीके से बूलियन कार्यों के सरलीकरण के लिए एक विधि शुरू की। इस पद्धति को कर्णघ मानचित्र विधि या के-मानचित्र विधि के रूप में जाना जाता है। यह एक ग्राफिकल विधि है, जिसमें 'एन' वेरिएबल्स के लिए 2 एन सेल होते हैं । आसन्न कोशिकाएं केवल एकल बिट स्थिति में भिन्न होती हैं।
2 से 5 चर के लिए कश्मीर मैप्स
K-Map विधि 2 चरों के 5 कार्यों के बूलियन कार्यों को कम करने के लिए सबसे उपयुक्त है। अब, एक-एक करके के-मैप्स के बारे में 2 से 5 वेरिएबल्स के बारे में चर्चा करते हैं।
2 चर K- नक्शा
2 चर के-मानचित्र में कोशिकाओं की संख्या चार है, क्योंकि चर की संख्या दो है। निम्नलिखित आंकड़ा दिखाता है2 variable K-Map।
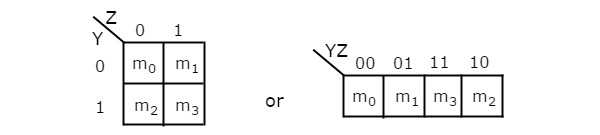
4 आसन्न न्यूनतम शर्तों को समूहीकृत करने की केवल एक संभावना है।
2 आसन्न न्यूनतम शर्तों को समूहीकृत करने के संभावित संयोजन {(m 0 , m 1 ), (m 2 , m 3 ), (m 0 , m 2 ) और (m 1 , m 3 )} हैं।
3 चर K- नक्शा
3 चर K- मानचित्र में कोशिकाओं की संख्या आठ है, क्योंकि चर की संख्या तीन है। निम्नलिखित आंकड़ा दिखाता है3 variable K-Map।
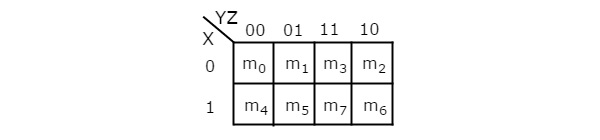
8 आसन्न न्यूनतम शर्तों को समूहीकृत करने की केवल एक संभावना है।
4 आसन्न न्यूनतम पदों को समूहीकृत करने के संभावित संयोजन {(m 0 , m 1 , m 3 , m 2 ), (m 4 , m 5 , m 7 , m 6 ), (m 0 , m 1 , m 4 , m हैं 5 ), (एम 1 , एम 3 , एम 5 , एम 7 ), (एम 3 , एम 2 , एम 7 , एम 6 ) और (एम 2 , एम 0 , एम 6 , एम 4 )}।
2 आसन्न न्यूनतम पदों को समूहीकृत करने के संभावित संयोजन {(m 0 , m 1 ), (m 1 , m 3 ), (m 3 , m 2 ), (m 2 , m 0 ), (m 4 , m 5 ) हैं , (एम 5 , एम 7 ), (एम 7 , एम 6 ), (एम 6 , एम 4 ), (एम 0 , एम 4 ), (एम 1 , एम 5 ), (एम 3 , एम 7 ) और ( एम 2 , एम 6 )}।
यदि x = 0 है, तो 3 चर K- मानचित्र 2 चर K- मानचित्र बन जाता है।
4 चर K- नक्शा
4 चर K- मानचित्र में कोशिकाओं की संख्या सोलह है, क्योंकि चर की संख्या चार है। निम्नलिखित आंकड़ा दिखाता है4 variable K-Map।
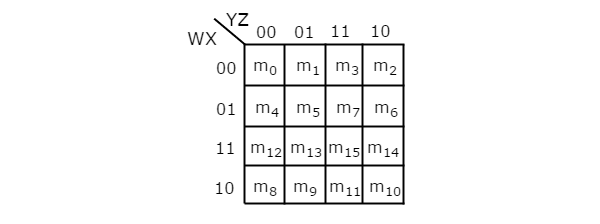
16 आसन्न न्यूनतम शर्तों को समूहीकृत करने की केवल एक संभावना है।
R 1 , R 2 , R 3 और R 4 को क्रमशः पहली पंक्ति, दूसरी पंक्ति, तीसरी पंक्ति और चौथी पंक्ति की न्यूनतम शर्तों को दर्शाता है। इसी तरह, सी 1 , सी 2 , सी 3 और सी 4 क्रमशः पहले कॉलम, दूसरे कॉलम, तीसरे कॉलम और चौथे कॉलम की न्यूनतम शर्तों को दर्शाता है। 8 आसन्न न्यूनतम शर्तों को समूहीकृत करने के संभावित संयोजन हैं {(R 1 , R 2 ), (R 2 , R 3 ), (R 3 , R 4 ), (R 4 , R 1 ), (C 1 , C 2 ) , (C 2 , C 3 ), (C 3 , C 4 ), (C 4 , C 1 )}।
यदि w = 0 है, तो 4 चर K-map 3 चर K-map बन जाता है।
5 चर K- नक्शा
5 चर K- मानचित्र में कोशिकाओं की संख्या बत्तीस है, क्योंकि चर की संख्या 5. निम्न आकृति दर्शाती है 5 variable K-Map।

32 आसन्न न्यूनतम शर्तों को समूहीकृत करने की केवल एक संभावना है।
16 आसन्न न्यूनतम शर्तों को समूहीकृत करने की दो संभावनाएँ हैं। यानी, मी 0 से एम 15 और एम 16 से एम 31 तक न्यूनतम अवधि ।
यदि v = 0 है, तो 5 चर K- मानचित्र 4 चर K- मानचित्र बन जाता है।
उपर्युक्त सभी के-नक्शों में, हमने विशेष रूप से न्यूनतम शर्तों के अंकन का उपयोग किया है। इसी तरह, आप विशेष रूप से अधिकतम शर्तें नोटेशन का उपयोग कर सकते हैं।
K- मैप्स का उपयोग करके बूलियन फ़ंक्शंस का न्यूनतमकरण
यदि हम उन इनपुटों के संयोजन पर विचार करते हैं जिनके लिए बूलियन फ़ंक्शन '1' है, तो हमें बूलियन फ़ंक्शन मिलेगा, जो कि standard sum of products K-map को सरल बनाने के बाद प्रपत्र।
इसी तरह, अगर हम उन इनपुटों के संयोजन पर विचार करते हैं जिनके लिए बूलियन फ़ंक्शन '0' है, तो हम बूलियन फ़ंक्शन को प्राप्त करेंगे, जो कि में है standard product of sums K-map को सरल बनाने के बाद प्रपत्र।
इनका पालन करें rules for simplifying K-maps उत्पादों के मानक योग प्राप्त करने के लिए।
बूलियन फ़ंक्शन में मौजूद चर की संख्या के आधार पर संबंधित के-मानचित्र का चयन करें।
यदि बूलियन फ़ंक्शन को न्यूनतम शर्तों के योग के रूप में दिया जाता है, तो उन्हें के-मैप में संबंधित मिनिमम सेल में रखें। यदि बूलियन फ़ंक्शन को उत्पादों के योग के रूप में दिया जाता है, तो उन्हें के-मैप के सभी संभावित कोशिकाओं में रखें, जिसके लिए दिए गए उत्पाद की शर्तें मान्य हैं।
आस-पास के लोगों की अधिकतम संख्या को समूहीकृत करने की संभावनाओं की जाँच करें। यह दो की शक्तियां होनी चाहिए। दो की उच्चतम शक्ति से शुरू करें और दो की अधिकतम शक्ति तक। उच्चतम शक्ति K- मानचित्र में माने जाने वाले चरों की संख्या के बराबर है और सबसे कम शक्ति शून्य है।
प्रत्येक समूह या तो एक शाब्दिक या एक उत्पाद शब्द देगा। इसे यह भी कहा जाता हैprime implicant। प्रमुख अधिपति कहा जाता हैessential prime implicant, अगर कम से कम एकल '1' को किसी अन्य समूह के साथ कवर नहीं किया जाता है, लेकिन केवल उस समूहीकरण को कवर किया जाता है।
सभी प्रमुख इम्प्लिकेंट्स और आवश्यक प्राइम इम्प्लिकेंट्स पर ध्यान दें। सरलीकृत बूलियन फ़ंक्शन में सभी आवश्यक प्राइम इम्प्लिकेंट्स और केवल आवश्यक प्राइम इम्प्लिकेंट्स होते हैं।
Note 1 - यदि आउटपुट इनपुट के कुछ संयोजन के लिए परिभाषित नहीं हैं, तो उन आउटपुट मानों के साथ प्रतिनिधित्व किया जाएगा don’t care symbol ‘x’। इसका मतलब है, हम उन्हें '0' या '1' मान सकते हैं।
Note 2- अगर देखभाल की शर्तें भी मौजूद नहीं हैं, तो के-मैप की संबंधित कोशिकाओं में 'x' को न रखें। केवल 'x' की परवाह न करें, जो कि आस-पास के लोगों की अधिकतम संख्या के लिए सहायक हो। उन मामलों में, '1' के रूप में परवाह न करें।
उदाहरण
हमें करने दो simplify निम्नलिखित बूलियन फ़ंक्शन, f(W, X, Y, Z)= WX’Y’ + WY + W’YZ’ K- मानचित्र का उपयोग करना।
दिए गए बूलियन फ़ंक्शन उत्पादों के रूप में हैं। यह 4 चर डब्ल्यू, एक्स, वाई एंड जेड है। इसलिए, हमें इसकी आवश्यकता है4 variable K-map। 4 variable K-map दिए गए उत्पाद की शर्तों के अनुरूप लोगों को निम्नलिखित आकृति में दिखाया गया है।
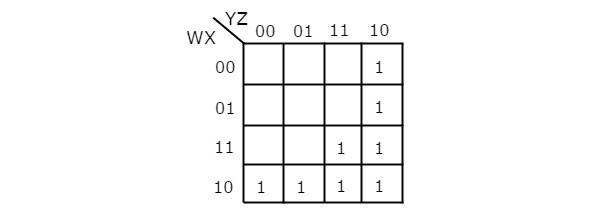
यहाँ, 1s को K-map की निम्नलिखित कोशिकाओं में रखा गया है।
कोशिकाएं, जो पंक्ति 4 और स्तंभ 1 और 2 के प्रतिच्छेदन के लिए सामान्य हैं, उत्पाद अवधि के अनुरूप हैं, WX’Y’।
कोशिकाएं, जो पंक्तियों 3 और 4 के चौराहे पर आम हैं और कॉलम 3 और 4 उत्पाद अवधि के अनुरूप हैं, WY।
कोशिकाओं, जो 1 और 2 और स्तंभ 4 के प्रतिच्छेदन के लिए आम हैं, उत्पाद अवधि के अनुरूप हैं, W’YZ’।
16 निकटवर्ती या 8 आसन्न लोगों के समूह की कोई संभावना नहीं है। 4 आसन्न लोगों के समूह की तीन संभावनाएं हैं। इन तीन समूहों के बाद, कोई भी ऐसा नहीं बचा है जिसे अनियंत्रित किया गया हो। इसलिए, हमें 2 आसन्न लोगों के समूहन के लिए जाँच करने की आवश्यकता नहीं है। 4 variable K-map इन तीनों के साथ groupings निम्नलिखित आकृति में दिखाया गया है।

यहां, हमें तीन प्रमुख प्रत्यारोपण WX ', WY & YZ' मिले। ये सभी प्राइम इंप्लांट्स हैंessential निम्नलिखित कारणों से।
दो वाले (m8 & m9)चौथी पंक्ति के समूहन को किसी अन्य समूह द्वारा कवर नहीं किया जाता है। केवल चौथी पंक्ति समूहन में उन दो को शामिल किया गया है।
अविवाहित (m15)चौकोर आकार के समूहन को किसी अन्य समूह द्वारा कवर नहीं किया जाता है। केवल चौकोर आकार समूह समूहीकरण को कवर करता है।
दो वाले (m2 & m6)चौथे स्तंभ समूह को किसी अन्य समूह द्वारा कवर नहीं किया गया है। केवल चौथा स्तंभ समूह उन दो को कवर करता है।
इसलिए simplified Boolean function है
f = WX’ + WY + YZ’
इनका पालन करें rules for simplifying K-maps रकम के मानक उत्पाद प्राप्त करने के लिए।
बूलियन फ़ंक्शन में मौजूद चर की संख्या के आधार पर संबंधित के-मानचित्र का चयन करें।
यदि बूलियन फ़ंक्शन को मैक्स शब्दों के उत्पाद के रूप में दिया जाता है, तो के-मैप में संबंधित मैक्स टर्म कोशिकाओं पर शून्य रखें। यदि बूलियन फ़ंक्शन को रकम फॉर्म के उत्पाद के रूप में दिया जाता है, तो ज़ीरो को के-मैप के सभी संभावित कोशिकाओं में रखें, जिसके लिए दिए गए योग शब्द मान्य हैं।
आसन्न शून्य की अधिकतम संख्या को समूहीकृत करने की संभावनाओं की जाँच करें। यह दो की शक्तियां होनी चाहिए। दो की उच्चतम शक्ति से शुरू करें और दो की अधिकतम शक्ति तक। उच्चतम शक्ति K- मानचित्र में माने जाने वाले चरों की संख्या के बराबर है और सबसे कम शक्ति शून्य है।
प्रत्येक समूह या तो एक शाब्दिक या एक योग शब्द देगा। इसे यह भी कहा जाता हैprime implicant। प्रमुख अधिपति कहा जाता हैessential prime implicant, अगर कम से कम एकल '0' को किसी अन्य समूह के साथ कवर नहीं किया जाता है, लेकिन केवल उस समूहीकरण को कवर किया जाता है।
सभी प्रमुख इम्प्लिकेंट्स और आवश्यक प्राइम इम्प्लिकेंट्स पर ध्यान दें। सरलीकृत बूलियन फ़ंक्शन में सभी आवश्यक प्राइम इम्प्लिकेंट्स और केवल आवश्यक प्राइम इम्प्लिकेंट्स होते हैं।
Note- अगर देखभाल की शर्तें भी मौजूद नहीं हैं, तो के-मैप की संबंधित कोशिकाओं में 'x' को न रखें। केवल 'x' की परवाह न करें, जो आस-पास के शून्य की अधिकतम संख्या को समूहीकृत करने में सहायक हो। उन मामलों में, परवाह न करें मान को '0' के रूप में देखें।
उदाहरण
हमें करने दो simplify निम्नलिखित बूलियन फ़ंक्शन, $ f \ left (X, Y, Z \ right) = \ prod M \ बाएँ (0,1,2,4 \ दाएँ) $ K-map का उपयोग करके।
दिए गए बूलियन फ़ंक्शन मैक्स शर्तों के उत्पाद में है। यह 3 चर X, Y & Z है। इसलिए, हमें 3 चर K-map की आवश्यकता है। दिए गए अधिकतम शब्द M 0 , M 1 , M 2 और M 4 हैं । ३variable K-map दिए गए अधिकतम शब्दों के अनुरूप शून्य के साथ निम्न आकृति में दिखाया गया है।

8 आसन्न शून्य या 4 आसन्न शून्य समूह बनाने की कोई संभावना नहीं है। 2 निकटवर्ती शून्य को समूहीकृत करने की तीन संभावनाएँ हैं। इन तीन समूहों के बाद, एक भी शून्य नहीं बचा है जैसा कि अनियंत्रित है। 3 variable K-map इन तीनों के साथ groupings निम्नलिखित आकृति में दिखाया गया है।

यहाँ, हमें तीन प्रधान प्रत्यारोपण X + Y, Y + Z & Z + X मिले हैं। ये सभी प्रमुख निहितार्थ हैं essential क्योंकि प्रत्येक समूह में एक शून्य को उनके व्यक्तिगत समूहों के अलावा किसी अन्य समूह द्वारा कवर नहीं किया जाता है।
इसलिए simplified Boolean function है
f = (X + Y).(Y + Z).(Z + X)
इस तरह, हम आसानी से K- मानचित्र विधि का उपयोग करके 5 चर तक बूलियन कार्यों को सरल कर सकते हैं। 5 से अधिक चरों के लिए, K-Maps का उपयोग करके कार्यों को सरल बनाना मुश्किल है। क्योंकि, की संख्याcells K- मैप में मिलता है doubled एक नया चर शामिल करके।
इस के कारण आसन्न लोगों (मिनट की शर्तें) या आसन्न शून्य (अधिकतम पद) की जाँच और समूहीकरण जटिल हो जाएगा। हम चर्चा करेंगेTabular method के-मैप विधि की कठिनाइयों को दूर करने के लिए अगले अध्याय में।