डिजिटल सर्किट - त्वरित गाइड
यदि किसी संख्या प्रणाली का आधार या मूलांक 'r' है, तो उस संख्या प्रणाली में मौजूद संख्याएं शून्य से लेकर r-1 तक होती हैं। उस संख्या प्रणाली में मौजूद कुल संख्या 'आर' है। इसलिए, हम मूलांक के मानों को दो से अधिक या उसके बराबर मानकर, विभिन्न संख्या प्रणाली प्राप्त करेंगे।
इस अध्याय में, आइए हम इसके बारे में चर्चा करें popular number systemsऔर संबंधित संख्या प्रणाली में एक संख्या का प्रतिनिधित्व कैसे करें। निम्नलिखित संख्या प्रणाली सबसे अधिक उपयोग की जाती हैं।
- दशमलव संख्या प्रणाली
- बाइनरी नंबर सिस्टम
- ऑक्टल नंबर सिस्टम
- हेक्साडेसिमल संख्या प्रणाली
दशमलव संख्या प्रणाली
base या दशमलव संख्या प्रणाली का मूलांक है 10। तो, इस संख्या प्रणाली में 0 से 9 तक की संख्या का उपयोग किया जाता है। संख्या का वह भाग जो बाईं ओर स्थित हैdecimal pointपूर्णांक भाग के रूप में जाना जाता है। इसी प्रकार, संख्या का वह भाग जो दशमलव बिंदु के दाईं ओर स्थित होता है, भिन्नात्मक भाग के रूप में जाना जाता है।
इस संख्या प्रणाली में, 10 0 , 10 1 , 10 2 , 10 3 और इसी तरह दशमलव बिंदु के बाईं ओर के क्रमिक पदों । इसी तरह, दशमलव बिंदु के दाईं ओर स्थित पदों में 10 -1 , 10 -2 , 10 -3 और इसी तरह वजन होता है। इसका मतलब है, प्रत्येक स्थिति का विशिष्ट वजन है, जो हैpower of base 10
उदाहरण
इसपर विचार करें decimal number 1358.246। इस संख्या का पूर्णांक भाग 1358 है और इस संख्या का आंशिक भाग 0.246 है। अंक 8, 5, 3 और 1 में क्रमशः 100, 101, 10 2 और 10 3 का वजन है । इसी तरह, अंक 2, 4 और 6 में क्रमशः 10 -1 , 10 -2 और 10 -3 का वजन होता है।
Mathematically, हम इसे लिख सकते हैं
1358.246 = (1 × 10 3 ) + (3 × 10 2 ) + (5 × 10 1 ) + (8 × 10 0 ) + (2 × 10 -1 ) +
(4 × 10 -2 ) + (6 × 10 -3 )
दाहिने हाथ की ओर की शर्तों को सरल करने के बाद, हम दशमलव संख्या प्राप्त करेंगे, जो बाईं ओर है।
बाइनरी नंबर सिस्टम
सभी डिजिटल सर्किट और सिस्टम इस बाइनरी नंबर सिस्टम का उपयोग करते हैं। base या इस संख्या प्रणाली का मूलांक है 2। तो, इस संख्या प्रणाली में संख्या 0 और 1 का उपयोग किया जाता है।
संख्या का वह भाग, जो बाईं ओर स्थित है binary pointपूर्णांक भाग के रूप में जाना जाता है। इसी तरह, संख्या का हिस्सा, जो बाइनरी पॉइंट के दाईं ओर स्थित है, को आंशिक भाग के रूप में जाना जाता है।
इस संख्या प्रणाली में, द्विआधारी बिंदु के बाईं ओर के क्रमिक पदों में 2 0 , 2 1 , 2 2 , 2 3 और इसी तरह वजन होता है। इसी तरह, 2 -1 , 2 -2 , 2 -3 और इसी तरह के द्विआधारी बिंदु के दाईं ओर स्थितियां । इसका मतलब है, प्रत्येक स्थिति का विशिष्ट वजन है, जो हैpower of base 2।
उदाहरण
इसपर विचार करें binary number 1101.011। इस संख्या का पूर्णांक भाग 1101 है और इस संख्या का आंशिक भाग 0.011 है। पूर्णांक के अंक 1, 0, 1 और 1 में क्रमशः 2 0 , 2 1 , 2 2 , 2 3 का वजन होता है। इसी प्रकार, भिन्नात्मक भाग के अंक 0, 1 और 1 में क्रमशः 2 -1 , 2 -2 , 2 -3 का वजन होता है।
Mathematically, हम इसे लिख सकते हैं
1101.011 = (1 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 ) + (0 × 2 -1 ) +
(1 × 2 -2 ) + (1 × 2 -3 )
दाहिने हाथ की ओर की शर्तों को सरल करने के बाद, हमें एक दशमलव संख्या मिलेगी, जो कि बायीं ओर बाइनरी नंबर के बराबर है।
ऑक्टल नंबर सिस्टम
base या अष्टक संख्या प्रणाली का मूलांक है 8। तो, इस संख्या प्रणाली में 0 से 7 तक की संख्या का उपयोग किया जाता है। संख्या का वह भाग जो बाईं ओर स्थित हैoctal pointपूर्णांक भाग के रूप में जाना जाता है। इसी तरह, संख्या का वह हिस्सा जो अष्ट बिंदु के दाईं ओर स्थित होता है, भिन्नात्मक भाग के रूप में जाना जाता है।
इस संख्या प्रणाली में, 8 , 0 , 8 1 , 8 2 , 8 3 और इसी तरह के अष्ट बिंदु के बाईं ओर लगातार स्थिति होती है । इसी तरह, 8 , -1 , 8 -2 , 8 -3 वगैरह के अष्टक बिंदु के दाईं ओर लगातार स्थिति होती है । इसका मतलब है, प्रत्येक स्थिति का विशिष्ट वजन है, जो हैpower of base 8।
उदाहरण
इसपर विचार करें octal number 1457.236। इस संख्या का पूर्णांक भाग 1457 है और इस संख्या का आंशिक भाग 0.236 है। अंक 7, 5, 4 और 1 में क्रमशः 8 0 , 8 1 , 8 2 और 8 3 का वजन होता है। इसी तरह, अंक 2, 3 और 6 में क्रमशः 8 -1 , 8 -2 , 8 -3 का वजन है ।
Mathematically, हम इसे लिख सकते हैं
1457.236 = (1 × 8 3 ) + (4 × 8 2 ) + (5 × 8 1 ) + (7 × 8 0 ) + (2 × 8 -1 ) +
(3 × 8 -2 ) + (6 × 8 -3 )
दाहिने हाथ की ओर की शर्तों को सरल करने के बाद, हमें एक दशमलव संख्या मिलेगी, जो बाएं हाथ की तरफ अष्टक संख्या के बराबर है।
हेक्साडेसिमल नंबर सिस्टम
base या हेक्सा-दशमलव संख्या प्रणाली का मूलांक है 16। तो, इस संख्या प्रणाली में 0 से 9 तक की संख्या और ए से एफ तक के अक्षरों का उपयोग किया जाता है। हेक्सा-दशमलव अंकों के बराबर ए से एफ तक 10 से 15 हैं।
संख्या का वह भाग, जो बाईं ओर स्थित है hexadecimal pointपूर्णांक भाग के रूप में जाना जाता है। इसी तरह, संख्या का वह हिस्सा, जो हेक्सा-दशमलव बिंदु के दाईं ओर स्थित है, को आंशिक भाग के रूप में जाना जाता है।
इस संख्या प्रणाली में, हेक्सा-दशमलव बिंदु के बाईं ओर के क्रमिक स्थान जिनकी लंबाई 16 0 , 16 1 , 16 2 , 16 3 और इसी तरह है। इसी प्रकार, हेक्सा-दशमलव बिंदु के दाईं ओर स्थित पदों में 16 -1 , 16 -2 , 16 -3 और इसी तरह वजन होता है। इसका मतलब है, प्रत्येक स्थिति का विशिष्ट वजन है, जो हैpower of base 16।
उदाहरण
इसपर विचार करें Hexa-decimal number 1A05.2C4। इस संख्या का पूर्णांक भाग 1A05 है और इस संख्या का आंशिक भाग 0.2C4 है। अंक 5, 0, A और 1 का वजन क्रमशः 16 0 , 16 1 , 16 2 और 16 3 है। इसी तरह, अंक 2, सी और 4 में क्रमशः 16 -1 , 16 -2 और 16 -3 का वजन है ।
Mathematically, हम इसे लिख सकते हैं
1A05.2C4 = (1 × 16 3 ) + (10 × 16 2 ) + (0 × 16 1 ) + (5 × 16 0 ) + (2 × 16 -1 ) +
(12 × 16 -2 ) + (4 × 16 -3 )
दाहिने हाथ की ओर की शर्तों को सरल करने के बाद, हम एक दशमलव संख्या प्राप्त करेंगे, जो बाएँ हाथ पर हेक्सा-दशमलव संख्या के बराबर है।
पिछले अध्याय में, हमने चार प्रमुख संख्या प्रणाली देखी हैं। इस अध्याय में, समतुल्य मान ज्ञात करने के लिए संख्याओं को एक संख्या प्रणाली से दूसरी संख्या में परिवर्तित करते हैं।
दशमलव संख्या अन्य मामलों में रूपांतरण के लिए
यदि दशमलव संख्या में पूर्णांक भाग और भिन्नात्मक भाग दोनों होते हैं, तो दशमलव संख्या के दोनों भागों को व्यक्तिगत रूप से अन्य आधार में परिवर्तित करें। दशमलव संख्या को किसी भी आधार 'r' के समकक्ष संख्या में परिवर्तित करने के लिए इन चरणों का पालन करें।
कर division दशमलव संख्या का पूर्णांक भाग और successive quotientsआधार 'आर' के साथ और नीचे अंशों को तब तक नोट करें जब तक कि भागफल शून्य न हो। आधार 'आर' के समतुल्य संख्या के पूर्णांक भाग को प्राप्त करने के लिए रिवर्स ऑर्डर पर विचार करें। इसका मतलब है, पहले और आखिरी अवशेष क्रमशः कम से कम महत्वपूर्ण अंक और सबसे महत्वपूर्ण अंक दर्शाते हैं।
कर multiplication दशमलव संख्या के आंशिक भाग और successive fractionsआधार 'r' के साथ और जब तक परिणाम शून्य न हो तब तक नोट को नीचे रखें या समकक्ष अंकों की वांछित संख्या प्राप्त करें। आधार 'आर' के समतुल्य अंश के भिन्नात्मक भाग को प्राप्त करने के लिए कैरी के सामान्य अनुक्रम पर विचार करें।
द्विआधारी रूपांतरण के लिए दशमलव
दशमलव संख्या को उसके समतुल्य बाइनरी संख्या में परिवर्तित करते हुए निम्नलिखित दो प्रकार के ऑपरेशन होते हैं।
- आधार 2 के साथ पूर्णांक भाग और क्रमिक कोटेशन का विभाजन।
- बेस 2 के साथ आंशिक भाग और क्रमिक अंशों का गुणन।
Example
इसपर विचार करें decimal number 58.25। यहाँ, पूर्णांक भाग 58 और भिन्नात्मक भाग 0.25 है।
Step 1 - आधार 2 के साथ 58 और क्रमिक कोटियों का विभाजन।
| ऑपरेशन | लब्धि | शेष |
|---|---|---|
| 58/2 | 29 | 0 (LSB) |
| 29/2 | 14 | 1 |
| 14/2 | 7 | 0 |
| 7/2 | 3 | 1 |
| 3/2 | 1 | 1 |
| 1/2 | 0 | 1(MSB) |
⇒ (58) 10 = (111010) 2
इसलिए integer part समतुल्य बाइनरी संख्या है 111010।
Step 2 - बेस 2 के साथ 0.25 का गुणन और क्रमिक अंश।
| ऑपरेशन | परिणाम | कैरी |
|---|---|---|
| 0.25 x 2 | 0.5 | 0 |
| 0.5 x 2 | 1.0 | 1 |
| - | 0.0 | - |
⇒ (.25) 10 = (.01) 2
इसलिए fractional part समतुल्य बाइनरी संख्या है .01
⇒ ( 58.25) 10 = (111010.01) 2
इसलिए binary equivalent दशमलव संख्या 58.25 का 111010.01 है।
अष्टाधारी रूपांतरण के लिए दशमलव
दशमलव संख्या को उसके समकक्ष अष्टक संख्या में परिवर्तित करते हुए निम्नलिखित दो प्रकार के ऑपरेशन होते हैं।
बेस 8 के साथ पूर्णांक भाग और क्रमिक कोटेशन का विभाजन।
बेस 8 के साथ आंशिक भाग और क्रमिक अंशों का गुणन।
Example
इसपर विचार करें decimal number 58.25। यहाँ, पूर्णांक भाग 58 और भिन्नात्मक भाग 0.25 है।
Step 1 - आधार - के साथ ५ - और क्रमिक कोटियों का विभाजन।
| ऑपरेशन | लब्धि | शेष |
|---|---|---|
| 58/8 | 7 | 2 |
| 7/8 | 0 | 7 |
⇒ (58) 10 = (72) 8
इसलिए integer part समतुल्य अष्टक संख्या है 72।
Step 2 - बेस 8 के साथ 0.25 का गुणन और क्रमिक अंश।
| ऑपरेशन | परिणाम | कैरी |
|---|---|---|
| 0.25 x 8 | 2.00 | 2 |
| - | 0.00 | - |
⇒ (.25) 10 = (.2) 8
इसलिए fractional part समतुल्य अष्टक संख्या है ।2
⇒ (58.25) 10 = (72.2) 8
इसलिए octal equivalent दशमलव संख्या 58.25 72.2 है।
दशमलव से हेक्सा-दशमलव रूपांतरण
दशमलव संख्या को उसके समतुल्य हेक्सा-दशमलव संख्या में परिवर्तित करते हुए निम्नलिखित दो प्रकार के ऑपरेशन होते हैं।
- बेस 16 के साथ पूर्णांक भाग और क्रमिक कोटेशन का विभाजन।
- बेस 16 के साथ आंशिक भाग और क्रमिक अंशों का गुणन।
Example
इसपर विचार करें decimal number 58.25। यहाँ, पूर्णांक भाग 58 और दशमलव भाग 0.25 है।
Step 1 - आधार का विभाजन ५ - और क्रमिक आधारों का आधार १६ है।
| ऑपरेशन | लब्धि | शेष |
|---|---|---|
| 58/16 | 3 | 10 = एक |
| 3/16 | 0 | 3 |
⇒ (५ ⇒) १० = (३ ए) १६
इसलिए integer part समतुल्य हेक्सा-दशमलव संख्या 3 ए है।
Step 2 - बेस 16 के साथ 0.25 का गुणन और क्रमिक अंश।
| ऑपरेशन | परिणाम | कैरी |
|---|---|---|
| 0.25 x 16 | 4.00 | 4 |
| - | 0.00 | - |
⇒ (.25) 10 = (.4) 16
इसलिए fractional part समतुल्य हेक्सा-दशमलव संख्या 4 है।
⇒(58.25)10 = (3A.4)16
इसलिए Hexa-decimal equivalent दशमलव संख्या ५ number.२५ ३ ए ४ है।
द्विआधारी संख्या अन्य मामलों में रूपांतरण के लिए
किसी संख्या को बाइनरी से दशमलव में बदलने की प्रक्रिया एक बाइनरी नंबर को अन्य आधारों में परिवर्तित करने की प्रक्रिया के लिए अलग है। अब, एक बाइनरी नंबर को दशमलव, ऑक्टल और हेक्सा-दशमलव संख्या सिस्टम में एक-एक करके बदलने के बारे में चर्चा करते हैं।
दशमलव रूपांतरण के लिए द्विआधारी
बाइनरी नंबर को इसके समतुल्य दशमलव संख्या में परिवर्तित करने के लिए, पहले बाइनरी नंबर के बिट्स को संबंधित स्थिति भार के साथ गुणा करें और फिर सभी उत्पादों को जोड़ें।
Example
इसपर विचार करें binary number 1101.11।
Mathematically, हम इसे लिख सकते हैं
(1101.11) 2 = (1 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 ) + (1 × 2 -1 ) +
(1 × 2 -2 )
⇒ (1101.11) 2 = 8 + 4 + 0 + 1 + 0.5 + 0.25 = 13.75
⇒ (1101.11) 2 = (13.75) 10
इसलिए decimal equivalent बाइनरी नंबर 1101.11 की संख्या 13.75 है।
अष्टाधारी रूपांतरण के लिए द्विआधारी
हम जानते हैं कि बाइनरी और ऑक्टल नंबर सिस्टम के आधार क्रमशः 2 और 8 हैं। द्विआधारी संख्या के तीन बिट्स एक ऑक्टल अंक के बराबर हैं, चूंकि 2 3 = 8।
बाइनरी नंबर को इसके समकक्ष ऑक्टल नंबर में बदलने के लिए इन दो चरणों का पालन करें।
बाइनरी पॉइंट से शुरू करें और बाइनरी पॉइंट के दोनों तरफ 3 बिट्स के समूह बनाएं। यदि 3 बिट्स का समूह बनाते समय एक या दो बिट्स कम हैं, तो चरम पक्षों पर आवश्यक संख्या में शून्य शामिल करें।
3 बिट्स के प्रत्येक समूह के अनुरूप अष्टक अंक लिखें।
Example
इसपर विचार करें binary number 101110.01101।
Step 1 - बाइनरी पॉइंट के दोनों तरफ 3 बिट्स के समूह बनाएं।
101 110.011 01
यहां, द्विआधारी बिंदु के दाईं ओर, अंतिम समूह में केवल 2 बिट्स हैं। तो, 3 बिट्स के समूह के रूप में बनाने के लिए चरम पक्ष पर एक शून्य शामिल करें।
⇒ 101 110.011 010
Step 2 - 3 बिट्स के प्रत्येक समूह के अनुरूप ऑक्टल अंक लिखें।
⇒ (101 110.011 010) 2 = (56.32) 8
इसलिए octal equivalent बाइनरी नंबर 101110.01101 की संख्या 56.32 है।
हेक्सा-दशमलव रूपांतरण के लिए द्विआधारी
हम जानते हैं कि बाइनरी और हेक्सा-दशमलव संख्या प्रणाली के आधार क्रमशः 2 और 16 हैं। द्विआधारी संख्या के चार बिट्स एक हेक्सा-दशमलव अंक के बराबर है, चूंकि 2 4 = 16 है।
बाइनरी नंबर को इसके समतुल्य हेक्सा-दशमलव संख्या में परिवर्तित करने के लिए इन दो चरणों का पालन करें।
बाइनरी पॉइंट से शुरू करें और बाइनरी पॉइंट के दोनों तरफ 4 बिट्स के समूह बनाएं। यदि 4 बिट के समूह को बनाते समय कुछ बिट्स कम हैं, तो चरम पक्षों पर आवश्यक संख्या में शून्य शामिल करें।
4 बिट के प्रत्येक समूह के अनुरूप हेक्सा-दशमलव अंक लिखें।
Example
इसपर विचार करें binary number 101110.01101
Step 1 - बाइनरी पॉइंट के दोनों तरफ 4 बिट्स के समूह बनाएं।
10 1110.0110 1
यहां, पहले समूह में केवल 2 बिट्स हैं। तो, 4 बिट्स के समूह के रूप में बनाने के लिए चरम पक्ष पर दो शून्य शामिल करें। इसी तरह, अंतिम समूह को भी 4 बिट के समूह के रूप में बनाने के लिए चरम पक्ष पर तीन शून्य शामिल करें।
⇒ 0010 1110.0110 1000
Step 2 - 4 बिट के प्रत्येक समूह के अनुरूप हेक्सा-दशमलव अंक लिखें।
⇒ (0010 1110.0110 1000) 2 = (2E.68) 16
इसलिए Hexa-decimal equivalent बाइनरी नंबर 101110.01101 (2E.68) है।
अन्य मामलों में अष्टक संख्या रूपांतरण
एक संख्या को अष्टाधारी से दशमलव में बदलने की प्रक्रिया एक अष्टक संख्या को अन्य आधारों में परिवर्तित करने की प्रक्रिया से भिन्न होती है। अब, दशमलव, बाइनरी और हेक्सा-दशमलव संख्या प्रणाली में एक-एक करके ऑक्टल नंबर के रूपांतरण के बारे में चर्चा करते हैं।
अष्टाधारी दशमलव में रूपांतरण
एक ऑक्टल संख्या को उसके समतुल्य दशमलव संख्या में परिवर्तित करने के लिए, पहले ओक्टल संख्या के अंकों को संबंधित स्थिति भार के साथ गुणा करें और फिर उन सभी उत्पादों को जोड़ें।
Example
इसपर विचार करें octal number 145.23।
Mathematically, हम इसे लिख सकते हैं
(145.23) 8 = (1 × 8 2 ) + (4 × 8 1 ) + (5 × 8 0 ) + (2 × 8 -1 ) + (3 × 8 -2 )
⇒ (145.23) 8 = 64 + 32 + 5 + 0.25 + 0.05 = 101.3
⇒ (145.23) 8 = (101.3) 10
इसलिए decimal equivalent अष्टक संख्या 145.23 का 101.3 है।
अष्टाधारी बाइनरी रूपांतरण
एक ऑक्टल संख्या को बराबर बाइनरी नंबर में बदलने की प्रक्रिया बाइनरी ऑक्टल रूपांतरण के ठीक विपरीत है। प्रत्येक ऑक्टल अंक को 3 बिट्स के साथ दर्शाने से, हमें बराबर बाइनरी नंबर मिलेगा।
Example
इसपर विचार करें octal number 145.23।
3 बिट्स के साथ प्रत्येक अष्टक अंक का प्रतिनिधित्व करें।
(145.23) 8 = (001 100 101.010 011) 2
शून्य को हटाकर मान परिवर्तित नहीं होता है, जो चरम सीमा पर हैं।
⇒ (145.23) 8 = (1100101.010011) 2
इसलिए binary equivalent अष्टक संख्या 145.23 का 1100101.010011 है।
अष्टाधारी हेक्सा-दशमलव रूपांतरण में
अष्टक संख्या को उसके समतुल्य हेक्सा-दशमलव संख्या में परिवर्तित करने के लिए इन दो चरणों का पालन करें।
- ऑक्टल नंबर को इसके बराबर बाइनरी नंबर में बदलें।
- उपरोक्त बाइनरी नंबर को इसके समतुल्य हेक्सा-दशमलव संख्या में परिवर्तित करें।
Example
इसपर विचार करें octal number 145.23
पिछले उदाहरण में, हमें 1100101.010011 के रूप में अष्टक संख्या 145.23 के बाइनरी बराबर मिला।
हेक्सा-दशमलव रूपांतरण के लिए बाइनरी की प्रक्रिया का पालन करके, हम प्राप्त करेंगे
(1100101.010011) 2 = (65.4C) 16
⇒ (145.23) 8 = (65.4C) 16
इसलिए Hexa-decimal equivalentअष्टक वर्ग की संख्या 145.23 65.4 C है ।
हेक्सा-दशमलव संख्या अन्य मामलों में रूपांतरण के लिए
हेक्सा-दशमलव से दशमलव में एक संख्या को परिवर्तित करने की प्रक्रिया हेक्सा-दशमलव संख्या को अन्य आधारों में परिवर्तित करने की प्रक्रिया से भिन्न है। अब, हेक्सा-दशमलव संख्या को दशमलव, बाइनरी और ऑक्टल संख्या प्रणालियों में एक-एक करके रूपांतरण के बारे में चर्चा करते हैं।
हेक्सा-दशमलव दशमलव में रूपांतरण के लिए
हेक्सा-दशमलव संख्या को इसके समतुल्य दशमलव संख्या में परिवर्तित करने के लिए, पहले हेक्सा-दशमलव संख्या के अंकों को संबंधित स्थिति भार के साथ गुणा करें और फिर उन सभी उत्पादों को जोड़ें।
Example
इसपर विचार करें Hexa-decimal number 1A5.2
Mathematically, हम इसे लिख सकते हैं
(1A5.2) 16 = (1 × 16 2 ) + (10 × 16 1 ) + (5 × 16 0 ) + (2 × 16 -1 )
⇒ (1A5.2) 16 = 256 + 160 + 5 + 0.125 = 421.125
⇒ (1A5.2) 16 = (421.125) 10
इसलिए decimal equivalent हेक्सा-दशमलव संख्या 1 ए 5.2 की संख्या 421.125 है।
हेक्सा-दशमलव द्विआधारी रूपांतरण के लिए
हेक्सा-दशमलव संख्या को इसके समतुल्य द्विआधारी संख्या में बदलने की प्रक्रिया हेक्सा-दशमलव रूपांतरण के द्विआधारी के विपरीत है। 4 बिट्स के साथ प्रत्येक हेक्सा-दशमलव अंक का प्रतिनिधित्व करके, हम बराबर बाइनरी नंबर प्राप्त करेंगे।
Example
इसपर विचार करें Hexa-decimal number 65.4C
4 बिट्स के साथ प्रत्येक हेक्सा-दशमलव अंक का प्रतिनिधित्व करते हैं।
(65.4C) 6 = (0110 0101.0100 1100) 2
शून्य को हटाकर मान परिवर्तित नहीं होता है, जो दो चरम पक्षों पर हैं।
⇒ (65.4C) 16 = (1100101.010011) 2
इसलिए binary equivalent हेक्सा-दशमलव संख्या 65.4C का 1100101.010011 है।
ओक्टा-रूपांतरण के लिए हेक्सा-डेसीमल
हेक्सा-दशमलव संख्या को इसके समकक्ष अष्टक संख्या में परिवर्तित करने के लिए इन दो चरणों का पालन करें।
- हेक्सा-दशमलव संख्या को इसके समकक्ष बाइनरी नंबर में परिवर्तित करें।
- उपरोक्त बाइनरी नंबर को इसके समकक्ष अष्टक संख्या में परिवर्तित करें।
Example
इसपर विचार करें Hexa-decimal number 65.4C
पिछले उदाहरण में, हमें हेक्सा-दशमलव संख्या 65.4C के बराबर बाइनरी 1100101.010011 मिली।
अष्टाधारी रूपांतरण के लिए बाइनरी की प्रक्रिया का पालन करके, हम प्राप्त करेंगे
(1100101.010011) 2 = (145.23) 8
⇒ (65.4C) 16 = (145.23)
इसलिए octal equivalentहेक्सा -दशमलव संख्या 65.4 सी का 145.23 है।
हम निम्नलिखित दो समूहों में बाइनरी नंबर बना सकते हैं - Unsigned numbers तथा Signed numbers।
निरुपित अंक
अहस्ताक्षरित संख्याओं में केवल संख्या का परिमाण होता है। उनके पास कोई संकेत नहीं है। इसका मतलब है कि सभी अहस्ताक्षरित बाइनरी संख्या सकारात्मक हैं। दशमलव संख्या प्रणाली में के रूप में, संख्या के सामने सकारात्मक संकेत रखने सकारात्मक संख्या का प्रतिनिधित्व करने के लिए वैकल्पिक है। इसलिए, शून्य सहित सभी सकारात्मक संख्याओं को अहस्ताक्षरित संख्याओं के रूप में माना जा सकता है यदि सकारात्मक संकेत संख्या के सामने असाइन नहीं किया गया है।
हस्ताक्षर किए गए नंबर
हस्ताक्षरित संख्याओं में संख्या के संकेत और परिमाण दोनों होते हैं। आम तौर पर, संकेत को संख्या के सामने रखा जाता है। तो, हमें सकारात्मक संख्या के लिए सकारात्मक संकेत और नकारात्मक संख्या के लिए नकारात्मक संकेत पर विचार करना होगा। इसलिए, सभी नंबरों को हस्ताक्षरित संख्याओं के रूप में माना जा सकता है यदि संख्या के सामने संगत चिह्न सौंपा गया हो।
यदि साइन बिट शून्य है, जो इंगित करता है कि बाइनरी संख्या सकारात्मक है। इसी तरह, यदि साइन बिट एक है, जो इंगित करता है कि बाइनरी नंबर नकारात्मक है।
अन-हस्ताक्षरित बाइनरी नंबर का प्रतिनिधित्व
संयुक्त राष्ट्र के हस्ताक्षरित बाइनरी संख्या में मौजूद बिट्स धारण करते हैं magnitudeएक नंबर का। इसका मतलब है, अगर संयुक्त राष्ट्र के हस्ताक्षरित बाइनरी नंबर में है‘N’ बिट्स, फिर सभी N बिट्स संख्या के परिमाण का प्रतिनिधित्व करते हैं, क्योंकि इसमें कोई संकेत बिट नहीं है।
Example
इसपर विचार करें decimal number 108। इस संख्या के बाइनरी समकक्ष है1101100। यह अहस्ताक्षरित बाइनरी नंबर का प्रतिनिधित्व है।
( १० 11 ) १० = (११०११००) २
यह 7 बिट्स है। ये 7 बिट्स 108 की संख्या के परिमाण का प्रतिनिधित्व करते हैं।
हस्ताक्षरित बाइनरी नंबर का प्रतिनिधित्व
हस्ताक्षरित बाइनरी नंबर के सबसे महत्वपूर्ण बिट (MSB) का उपयोग संख्याओं के संकेत को इंगित करने के लिए किया जाता है। इसलिए, यह भी कहा जाता हैsign bit। साइन बिट में '0' रखकर पॉजिटिव साइन को दर्शाया गया है। इसी तरह, साइन बिट में '1' रखकर नकारात्मक चिन्ह का प्रतिनिधित्व किया जाता है।
यदि हस्ताक्षरित बाइनरी नंबर में 'N' बिट्स हैं, तो (N-1) बिट्स केवल संख्या के परिमाण का प्रतिनिधित्व करते हैं क्योंकि एक बिट (MSB) संख्या के संकेत का प्रतिनिधित्व करने के लिए आरक्षित है।
वहा तीन है types of representations हस्ताक्षरित बाइनरी नंबर के लिए
- साइन-मैग्नीट्यूड फॉर्म
- 1 का पूरक रूप
- 2 का पूरक रूप
इन सभी 3 रूपों में एक सकारात्मक संख्या का प्रतिनिधित्व समान है। लेकिन, केवल प्रत्येक रूप में नकारात्मक संख्या का प्रतिनिधित्व अलग-अलग होगा।
Example
इसपर विचार करें positive decimal number +108। इस संख्या के परिमाण का द्विआधारी समतुल्य 1101100 है। ये 7 बिट्स 108 की संख्या के परिमाण को दर्शाते हैं। चूंकि यह धनात्मक संख्या है, इसलिए साइन बिट को शून्य मानें, जिसे परिमाण के बाईं ओर रखा गया है।
( +108) 10 = (01101100) 2
इसलिए signed binary representationसकारात्मक दशमलव संख्या +108 है। तो, साइन-परिमाण के रूप में एक ही प्रतिनिधित्व मान्य है, 1 का पूरक रूप और 2 का दशमलव दशमलव सकारात्मक संख्या +108 है।
साइन-मैग्नीट्यूड फॉर्म
साइन-परिमाण रूप में, MSB का प्रतिनिधित्व करने के लिए उपयोग किया जाता है sign संख्या और शेष बिट्स का प्रतिनिधित्व करते हैं magnitudeसंख्या का। इसलिए, केवल अहस्ताक्षरित बाइनरी नंबर के बाईं ओर साइन बिट शामिल करें। यह प्रतिनिधित्व हस्ताक्षरित दशमलव संख्या प्रतिनिधित्व के समान है।
Example
इसपर विचार करें negative decimal number -108। इस संख्या का परिमाण 108 है। हम जानते हैं कि 108 का अहस्ताक्षरित बाइनरी प्रतिनिधित्व 1101100 है। इसमें 7 बिट्स हैं। ये सभी बिट्स परिमाण का प्रतिनिधित्व करते हैं।
चूंकि दी गई संख्या ऋणात्मक है, इसलिए साइन बिट को एक मानें, जिसे परिमाण के बाईं ओर रखा गया है।
(−108) 10 = (11101100) 2
इसलिए, -108 का संकेत-परिमाण प्रतिनिधित्व है 11101100।
1 का पूरक रूप
1 की संख्या के पूरक द्वारा प्राप्त किया जाता है complementing all the bitsहस्ताक्षरित बाइनरी नंबर। तो, 1 सकारात्मक संख्या का पूरक एक नकारात्मक संख्या देता है। इसी तरह, 1 का ऋणात्मक संख्या का पूरक एक सकारात्मक संख्या देता है।
इसका मतलब है, यदि आप साइन बिट सहित द्विआधारी संख्या के दो गुना 1 के पूरक हैं, तो आपको मूल हस्ताक्षरित बाइनरी नंबर मिलेगा।
Example
इसपर विचार करें negative decimal number -108। इस संख्या का परिमाण 108 है। हम जानते हैं कि 108 के हस्ताक्षरित द्विआधारी प्रतिनिधित्व 01101100 है।
यह 8 बिट्स है। इस संख्या का MSB शून्य है, जो सकारात्मक संख्या को इंगित करता है। शून्य का पूरक एक है और इसके विपरीत। तो, ऋणात्मक संख्या प्राप्त करने के लिए शून्य द्वारा अपने और अपनों द्वारा शून्य की जगह लें।
(−108) 10 = (10010011) 2
इसलिए 1’s complement of (108)10 है (10010011)2।
2 का पूरक रूप
एक द्विआधारी संख्या के 2 के पूरक द्वारा प्राप्त किया जाता है adding one to the 1’s complementहस्ताक्षरित बाइनरी नंबर। तो, 2 सकारात्मक संख्या का पूरक एक नकारात्मक संख्या देता है। इसी तरह, 2 का ऋणात्मक संख्या का पूरक एक सकारात्मक संख्या देता है।
इसका मतलब है, यदि आप द्विआधारी संख्या के दो गुणा 2 का प्रदर्शन करते हैं, जिसमें साइन बिट भी शामिल है, तो आपको मूल हस्ताक्षरित बाइनरी नंबर मिलेगा।
Example
इसपर विचार करें negative decimal number -108।
हम 1 का पूरक जानते हैं (108)10 है (10010011)2
2 की तारीफ (108) 10 = 1 की तारीफ (108) 10 + 1।
= 10010011 + 1
= 10010100
इसलिए 2’s complement of (108)10 है (10010100)2।
इस अध्याय में, हम बुनियादी अंकगणितीय संक्रियाओं के बारे में चर्चा करते हैं, जो कि 2 के पूरक विधि का उपयोग करके किसी भी दो हस्ताक्षरित बाइनरी संख्या पर किया जा सकता है। basic arithmetic operations जोड़ और घटाव हैं।
दो हस्ताक्षरित द्विआधारी संख्याओं का जोड़
दो हस्ताक्षरित बाइनरी नंबर ए एंड बी पर विचार करें, जो 2 के पूरक रूप में दर्शाए गए हैं। हम प्रदर्शन कर सकते हैंadditionइन दो संख्याओं में, जो दो अहस्ताक्षरित बाइनरी संख्याओं के जोड़ के समान है। लेकिन, यदि परिणामी राशि में साइन बिट से ले जाने का प्रावधान है, तो सही मूल्य प्राप्त करने के लिए इसे अनदेखा करें (अनदेखा करें)।
यदि परिणामी योग सकारात्मक है, तो आप सीधे इसका परिमाण जान सकते हैं। लेकिन, यदि परिणामी राशि ऋणात्मक है, तो परिमाण प्राप्त करने के लिए इसके 2 पूरक लें।
उदाहरण 1
हम प्रदर्शन करते हैं addition दो दशमलव संख्या के +7 and +4 2 की पूरक विधि का उपयोग करना।
2’s complement 5 बिट्स के साथ +7 और +4 का प्रतिनिधित्व नीचे दिखाया गया है।
(+7) 10 = (00111) 2
(+4) 10 = (00100) 2
इन दो संख्याओं का जोड़ है
(+7) 10 + (+ 4) 10 = (00111) 2 + (00100) 2
⇒ (+7) 10 + (+ 4) 10 = (01011) 2 ।
परिणामी राशि में 5 बिट्स होते हैं। तो, साइन बिट से कोई कैरी आउट नहीं है। संकेत बिट '0' इंगित करता है कि परिणामी योग हैpositive। तो, योग की संख्या दशमलव संख्या प्रणाली में 11 है। इसलिए, दो सकारात्मक संख्याओं के अलावा एक और सकारात्मक संख्या देगा।
उदाहरण 2
हम प्रदर्शन करते हैं addition दो दशमलव संख्या के -7 तथा -4 2 की पूरक विधि का उपयोग करना।
2’s complement 5 बिट्स के साथ -7 और -4 का प्रतिनिधित्व प्रत्येक नीचे दिखाया गया है।
(.7) 10 = (11001) 2
(.4) 10 = (11100) 2
इन दो संख्याओं का जोड़ है
(107) 10 + (−4) 10 = (11001) 2 + (11100) 2
⇒ ( 107) 10 + (−4) 10 = (110101) 2 ।
परिणामी योग में 6 बिट्स होते हैं। इस मामले में, हस्ताक्षर साइन बिट से प्राप्त किया जाता है। तो, हम इसे हटा सकते हैं
परिणाम निकालने के बाद परिणामी राशि (ant7) 10 + (104) 10 = है(10101)2।
संकेत बिट '1' इंगित करता है कि परिणामी योग है negative। तो, इसके 2 पूरक लेने से हमें परिणामी राशि का परिमाण 11 के रूप में दशमलव संख्या प्रणाली में मिल जाएगा। इसलिए, दो नकारात्मक संख्याओं के अलावा एक और नकारात्मक संख्या देगा।
दो हस्ताक्षरित बाइनरी नंबर का घटाव
दो हस्ताक्षरित बाइनरी नंबर ए एंड बी पर विचार करें, जो 2 के पूरक रूप में दर्शाए गए हैं। हम जानते हैं कि 2 का सकारात्मक संख्या का पूरक ऋणात्मक संख्या देता है। इसलिए, जब भी हमें संख्या A से संख्या B को घटाना है, तो B का 2 पूरक लें और इसे A. So, आदि में जोड़ें।mathematically हम इसे लिख सकते हैं
A - B = A + (2's complement of B)
इसी तरह, यदि हमें संख्या B से संख्या A को घटाना है, तो A का 2 पूरक लें और इसे B. So, आदि में जोड़ें। mathematically हम इसे लिख सकते हैं
B - A = B + (2's complement of A)
तो, दो हस्ताक्षरित बाइनरी संख्याओं का घटाव दो हस्ताक्षरित बाइनरी संख्याओं के जोड़ के समान है। लेकिन, हमें संख्या का 2 पूरक लेना होगा, जिसे घटाया जाना चाहिए। यह हैadvantage2 की पूरक तकनीक। पालन करें, दो हस्ताक्षरित बाइनरी संख्याओं के अलावा के समान नियम।
उदाहरण 3
हम प्रदर्शन करते हैं subtraction दो दशमलव संख्या के +7 and +4 2 की पूरक विधि का उपयोग करना।
इन दो संख्याओं का घटाव है
(+7) 10 - (+4) 10 = (+7) 10 + ()4) 10 ।
2’s complement 5 बिट्स के साथ +7 और -4 का प्रतिनिधित्व प्रत्येक नीचे दिखाया गया है।
(+7) 10 = (00111) 2
(+4) 10 = (11100) 2
⇒ (+7) 10 + (+4) 10 = (00111) 2 + (11100) 2 = (00011) 2
यहाँ, साइन बिट से प्राप्त कैरी। तो, हम इसे हटा सकते हैं। कैरी हटाने के बाद परिणामी राशि है
(+7) 10 + (+4) 10 =(00011)2
संकेत बिट '0' इंगित करता है कि परिणामी योग है positive। तो, इसकी संख्या दशमलव संख्या प्रणाली में 3 है। इसलिए, दो दशमलव संख्याओं का घटाव +7 और +4 +3 है।
उदाहरण 4
हम प्रदर्शन करते हैं subtraction of दो दशमलव संख्या +4 तथा +7 2 की पूरक विधि का उपयोग करना।
इन दो संख्याओं का घटाव है
(+4) 10 - (+7) 10 = (+4) 10 + (107) 10 ।
2’s complement 5 बिट्स के साथ +4 और -7 का प्रतिनिधित्व प्रत्येक नीचे दिखाया गया है।
(+4) 10 = (00100) 2
(- = ) १० = (११००१) २
⇒ (+4) 10 + (-7) 10 = (00100) 2 + (11001) 2 = (11101) 2
यहां, साइन बिट से कैरी नहीं लिया जाता है। संकेत बिट '1' इंगित करता है कि परिणामी योग हैnegative। तो, 2 के पूरक लेने से हम दशमलव संख्या प्रणाली में 3 के रूप में परिणामी राशि का परिमाण प्राप्त करेंगे। इसलिए, दो दशमलव संख्याओं का घटाव +4 और +7 -3 है।
कोडिंग में, जब संख्याओं या अक्षरों को प्रतीकों के एक विशिष्ट समूह द्वारा दर्शाया जाता है, तो यह कहा जाता है कि संख्या या अक्षर को एन्कोड किया जा रहा है। प्रतीकों के समूह को कहा जाता हैcode। डिजिटल डेटा को बिट्स के समूह के रूप में दर्शाया, संग्रहीत और प्रेषित किया जाता है। बिट्स के इस समूह को भी कहा जाता हैbinary code।
बाइनरी कोड को दो प्रकारों में वर्गीकृत किया जा सकता है।
- भारित कोड
- बिना कोड के कोड
यदि कोड में स्थिति भार है, तो यह कहा जाता है weighted code। अन्यथा, यह एक अनकवर्ड कोड है। भारित कोड को सकारात्मक रूप से भारित कोड और नकारात्मक रूप से भारित कोड के रूप में वर्गीकृत किया जा सकता है।
दशमलव अंकों के लिए बाइनरी कोड
निम्न तालिका दशमलव अंक 0 से 9 के लिए विभिन्न बाइनरी कोड दिखाती है।
| दशांश अंक | 8421 संहिता | 2421 कोड | 84-2-1 कोड | अतिरिक्त 3 कोड |
|---|---|---|---|---|
| 0 | 0000 | 0000 | 0000 | 0011 |
| 1 | 0001 | 0001 | 0111 | 0100 |
| 2 | 0010 | 0010 | 0110 | 0101 |
| 3 | 0011 | 0011 | 0101 | 0110 |
| 4 | 0100 | 0100 | 0100 | 0111 |
| 5 | 0101 | 1011 | 1011 | 1000 |
| 6 | 0110 | 1100 | 1010 | 1001 |
| 7 | 0111 | 1101 | 1001 | 1010 |
| 8 | 1000 | 1110 | 1000 | 1011 |
| 9 | 1001 | 1111 | 1111 | 1100 |
हमारे पास दशमलव संख्या प्रणाली में 10 अंक हैं। बाइनरी में इन 10 अंकों का प्रतिनिधित्व करने के लिए, हमें न्यूनतम 4 बिट्स की आवश्यकता होती है। लेकिन, 4 बिट्स के साथ शून्य और लोगों के 16 अद्वितीय संयोजन होंगे। चूंकि, हमारे पास केवल 10 दशमलव अंक हैं, शून्य और अन्य के 6 संयोजन की आवश्यकता नहीं है।
8 4 2 1 कोड
इस कोड का वजन 8, 4, 2 और 1 है।
इस कोड में सभी सकारात्मक भार हैं। तो, यह एक हैpositively weighted code।
इस कोड को भी कहा जाता है natural BCD (बाइनरी कोडेड दशमलव) code।
Example
आइए हम दशमलव संख्या 786 के बीसीडी के बराबर पाते हैं। इस संख्या में 3 दशमलव अंक 7, 8 और 6 हैं। तालिका से, हम क्रमशः 7, 8 और 6 के बीसीडी (8421) कोड लिख सकते हैं, 0111, 1000 और 0110। ।
∴ (786)10 = (011110000110)BCD
BCD प्रतिनिधित्व में 12 बिट्स होते हैं, क्योंकि दशमलव अंकों के प्रत्येक BCD कोड में 4 बिट्स होते हैं।
2 4 2 1 कोड
इस कोड का वजन 2, 4, 2 और 1 है।
इस कोड में सभी सकारात्मक भार हैं। तो, यह एक हैpositively weighted code।
यह एक unnatural BCDकोड। अप्राकृतिक बीसीडी कोड के वजन का योग 9 के बराबर है।
यह है एक self-complementingकोड। स्व-पूरक कोड 9 के दशमलव संख्या का पूरक प्रदान करते हैं, बस इसके समकक्ष 2421 प्रतिनिधित्व में 1 और 0 का अंतर करके।
Example
आइए हम दशमलव संख्या 786 के 2421 के बराबर पाते हैं। इस संख्या में 3 दशमलव अंक 7, 8 और 6 हैं। तालिका से, हम क्रमशः 7, 8 और 6 के 2421 कोड 1101, 1110 और 1100 लिख सकते हैं।
इसलिए, दशमलव संख्या 786 के बराबर 2421 है 110111101100।
8 4 -2 -1 कोड
इस कोड का वजन 8, 4, -2 और -1 है।
इस कोड में पॉजिटिव वेट के साथ-साथ निगेटिव वेट भी है। तो, यह एक हैnegatively weighted code।
यह एक unnatural BCD कोड।
यह है एक self-complementing कोड।
Example
आइए हम दशमलव संख्या 786 के 8 4-2-1 के बराबर पाते हैं। इस संख्या में 3 दशमलव 7, 8 और 6 अंक हैं। तालिका से, हम 8 4 -2 -1 कोड 7, 8 और 6 लिख सकते हैं। क्रमशः 1001, 1000 और 1010 हैं।
इसलिए, 8 4 -2 -1 दशमलव संख्या 786 के बराबर है 100110001010।
अतिरिक्त 3 कोड
इस कोड में कोई वज़न नहीं है। तो, यह एक हैun-weighted code।
हम उस दशमलव संख्या के बाइनरी समकक्ष के लिए तीन (0011) जोड़कर एक दशमलव संख्या के अतिरिक्त 3 कोड प्राप्त करेंगे। इसलिए, इसे अतिरिक्त 3 कोड कहा जाता है।
यह है एक self-complementing कोड।
Example
आइए हम दशमलव संख्या 786 के अतिरिक्त 3 के बराबर पाते हैं। इस संख्या में 3 दशमलव 7, 8 और 6 अंक हैं। तालिका से, हम क्रमशः 7, 8 और 6 के अतिरिक्त 3 कोड लिख सकते हैं 1010, 1011 और 1001।
इसलिए, दशमलव संख्या 786 के अतिरिक्त 3 बराबर है 101010111001
ग्रे कोड
निम्न तालिका प्रत्येक 4-बिट बाइनरी कोड के अनुरूप 4-बिट ग्रे कोड दिखाती है।
| दशमलव संख्या | बाइनरी कोड | ग्रे कोड |
|---|---|---|
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
| 8 | 1000 | 1100 |
| 9 | 1001 | 1101 |
| 10 | 1010 | 1111 |
| 1 1 | 1011 | 1110 |
| 12 | 1100 | 1010 |
| 13 | 1101 | 1011 |
| 14 | 1110 | 1001 |
| 15 | 1111 | 1000 |
इस कोड में कोई वज़न नहीं है। तो, यह एक हैun-weighted code।
उपरोक्त तालिका में, क्रमिक ग्रे कोड केवल एक बिट स्थिति में भिन्न होते हैं। इसलिए, इस कोड को कहा जाता हैunit distance कोड।
ग्रे कोड रूपांतरण के लिए बाइनरी कोड
बाइनरी कोड को इसके समकक्ष ग्रे कोड में बदलने के लिए इन चरणों का पालन करें।
दिए गए बाइनरी कोड पर विचार करें और MSB के बाईं ओर एक शून्य रखें।
शून्य से शुरू होने वाले क्रमिक दो बिट्स की तुलना करें। यदि 2 बिट समान हैं, तो आउटपुट शून्य है। अन्यथा, आउटपुट एक है।
ग्रे कोड प्राप्त होने तक एलएसबी के उपरोक्त चरण को दोहराएं।
Example
तालिका से, हम जानते हैं कि बाइनरी कोड 1000 से संबंधित ग्रे कोड 1100 है। अब, उपरोक्त प्रक्रिया का उपयोग करके इसे सत्यापित करते हैं।
दिया गया है, बाइनरी कोड 1000 है।
Step 1 - एमएसबी के बाईं ओर शून्य रखकर, बाइनरी कोड 01000 होगा।
Step 2 - नए बाइनरी कोड के क्रमिक दो बिट्स की तुलना करके, हमें ग्रे कोड मिलेगा 1100।
हम जानते हैं कि बिट्स 0 और 1 अनुरूप वोल्टेज के दो अलग-अलग रेंज के अनुरूप हैं। तो, एक सिस्टम से दूसरे में बाइनरी डेटा के प्रसारण के दौरान, शोर भी जोड़ा जा सकता है। इसके कारण, अन्य सिस्टम पर प्राप्त आंकड़ों में त्रुटियां हो सकती हैं।
इसका मतलब है कि थोड़ा 0 1 में बदल सकता है या थोड़ा 1 1 में बदल सकता है। हम शोर के हस्तक्षेप से बच नहीं सकते हैं। लेकिन, हम मूल डेटा को पहले यह पता लगाकर वापस पा सकते हैं कि क्या कोई त्रुटि मौजूद है और फिर उन त्रुटियों को ठीक कर रहा है या नहीं। इस उद्देश्य के लिए, हम निम्नलिखित कोड का उपयोग कर सकते हैं।
- कोड का पता लगाने में त्रुटि
- त्रुटि सुधार कोड
Error detection codes- प्राप्त डेटा (बिट स्ट्रीम) में मौजूद त्रुटि (एस) का पता लगाने के लिए उपयोग किया जाता है। इन कोडों में कुछ बिट्स शामिल हैं, जो मूल बिट स्ट्रीम में शामिल (संलग्न) हैं। ये कोड त्रुटि का पता लगाते हैं, यदि यह मूल डेटा (बिट स्ट्रीम) के प्रसारण के दौरान होता है।Example - पैरिटी कोड, हैमिंग कोड।
Error correction codes- प्राप्त डेटा (बिट स्ट्रीम) में मौजूद त्रुटि (ओं) को सही करने के लिए उपयोग किया जाता है ताकि, हम मूल डेटा प्राप्त करें। त्रुटि सुधार कोड भी त्रुटि पहचान कोड की समान रणनीति का उपयोग करते हैं।Example - हैमिंग कोड।
इसलिए, त्रुटियों का पता लगाने और उन्हें ठीक करने के लिए, अतिरिक्त बिट्स को ट्रांसमिशन के समय डेटा बिट्स में जोड़ा जाता है।
समानता कोड
एक समता बिट को MSB के बाईं ओर या मूल बिट स्ट्रीम के LSB के दाईं ओर शामिल करना आसान है। दो प्रकार के समता कोड हैं, अर्थात् समता कोड और विषम समता कोड चुना जा रहा है जो समानता के प्रकार पर आधारित है।
समता संहिता
समरूप बिट का मान शून्य होना चाहिए, बाइनरी कोड में मौजूद लोगों की संख्या भी। अन्यथा, यह एक होना चाहिए। ताकि, उपस्थित लोगों की संख्या भीeven parity code। यहां तक कि समता कोड में डेटा बिट और समता बिट शामिल हैं।
निम्न तालिका से पता चलता है even parity codesप्रत्येक 3-बिट बाइनरी कोड के अनुरूप। यहां, समरूप बिट को भी बाइनरी कोड के एलएसबी के दाईं ओर शामिल किया गया है।
| बाइनरी कोड | समता बिट | समता संहिता |
|---|---|---|
| 000 | 0 | 0000 |
| 001 | 1 | 0011 |
| 010 | 1 | 0101 |
| 011 | 0 | 0110 |
| 100 | 1 | 1001 |
| 101 | 0 | 1010 |
| 110 | 0 | 1100 |
| 111 | 1 | 1111 |
यहां, सम समता कोड में मौजूद बिट्स की संख्या 4 है। इसलिए, सम समता कोड में सम संख्या वालों की संख्या 0, 2 और 4 है।
यदि दूसरी प्रणाली को इनमें से एक समता कोड प्राप्त होता है, तो प्राप्त आंकड़ों में कोई त्रुटि नहीं है। समता बिट के अलावा अन्य बिट्स बाइनरी कोड के समान हैं।
यदि अन्य प्रणाली समता कोड के अलावा अन्य प्राप्त करती है, तो प्राप्त आंकड़ों में एक त्रुटि होगी। इस स्थिति में, हम मूल बाइनरी कोड की भविष्यवाणी नहीं कर सकते क्योंकि हम त्रुटि की बिट स्थिति (ओं) को नहीं जानते हैं।
इसलिए, समता बिट भी प्राप्त समानता कोड में त्रुटि का पता लगाने के लिए उपयोगी है। लेकिन, त्रुटि को ठीक करने के लिए यह पर्याप्त नहीं है।
अजीब समानता कोड
यदि बाइनरी कोड में मौजूद विषम संख्या में विषम समता बिट का मान शून्य होना चाहिए। अन्यथा, यह एक होना चाहिए। ताकि, उपस्थित लोगों की विषम संख्याodd parity code। विषम समता कोड में डेटा बिट्स और विषम समता बिट होते हैं।
निम्न तालिका से पता चलता है odd parity codesप्रत्येक 3-बिट बाइनरी कोड के अनुरूप। यहां, विषम समता बिट द्विआधारी कोड के एलएसबी के दाईं ओर शामिल है।
| बाइनरी कोड | विचित्रता बिट | अजीब समानता कोड |
|---|---|---|
| 000 | 1 | 0001 |
| 001 | 0 | 0010 |
| 010 | 0 | 0100 |
| 011 | 1 | 0111 |
| 100 | 0 | 1000 |
| 101 | 1 | 1011 |
| 110 | 1 | 1101 |
| 111 | 0 | 1110 |
यहाँ, विषम समता कोड में मौजूद बिट्स की संख्या 4 है। इसलिए, इन विषम समता कोड में लोगों की संभावित संख्या 1 और 3 है।
यदि दूसरी प्रणाली इन विषम समता कोडों में से एक प्राप्त करती है, तो प्राप्त आंकड़ों में कोई त्रुटि नहीं है। विषम समता बिट के अलावा अन्य बिट्स बाइनरी कोड के समान हैं।
यदि अन्य प्रणाली विषम समता कोड के अलावा अन्य प्राप्त करती है, तो प्राप्त आंकड़ों में एक त्रुटि है। इस स्थिति में, हम मूल बाइनरी कोड की भविष्यवाणी नहीं कर सकते क्योंकि हम त्रुटि की बिट स्थिति (ओं) को नहीं जानते हैं।
इसलिए, विषम समता बिट केवल प्राप्त समानता कोड में त्रुटि का पता लगाने के लिए उपयोगी है। लेकिन, त्रुटि को ठीक करने के लिए यह पर्याप्त नहीं है।
हैमिंग कोड
प्राप्त डेटा में मौजूद त्रुटि का पता लगाने और सुधार दोनों के लिए हैमिंग कोड उपयोगी है। यह कोड कई समानता बिट्स का उपयोग करता है और हमें इन समानता बिट्स को 2 की शक्तियों की स्थिति में रखना होगा।
minimum value of 'k' जिसके लिए निम्नलिखित संबंध सही है (वैध) और कुछ नहीं बल्कि समता बिट्स की आवश्यक संख्या है।
$$2^k\geq n+k+1$$
कहाँ पे,
'n' बाइनरी कोड (सूचना) में बिट्स की संख्या है
'k' समता बिट्स की संख्या है
इसलिए, हमिंग कोड में बिट्स की संख्या n + k के बराबर है।
चलो Hamming code है $b_{n+k}b_{n+k-1}.....b_{3}b_{2}b_{1}$ और समता बिट्स $p_{k}, p_{k-1}, ....p_{1}$। हम 'के' समता बिट्स को केवल 2 पदों की शक्तियों में रख सकते हैं। शेष बिट स्थितियों में, हम बाइनरी कोड के 'n' बिट्स रख सकते हैं।
आवश्यकता के आधार पर, हमिंग कोड बनाते समय या तो समता या विषम समता का उपयोग कर सकते हैं। लेकिन, प्राप्त आंकड़ों में मौजूद किसी भी त्रुटि को खोजने के लिए समान समता तकनीक का उपयोग किया जाना चाहिए।
खोजने के लिए इस प्रक्रिया का पालन करें parity bits।
का मान ज्ञात कीजिए p1बिट पदों 3 बी , 5 , बी 7 और इतने पर मौजूद लोगों की संख्या के आधार पर। इन सभी बिट पदों (प्रत्यय) के बराबर बाइनरी में 2 0 के स्थान मान में '1' है ।
का मान ज्ञात कीजिए p2बिट पदों 3 , बी 6 , बी 7 और इतने पर मौजूद लोगों की संख्या के आधार पर। इन सभी बिट पदों (प्रत्यय) को उनके समकक्ष बाइनरी में 2 1 के स्थान मान में '1' है ।
का मान ज्ञात कीजिए p3बिट पदों 5 बी , 6 , बी 7 और इतने पर मौजूद लोगों की संख्या के आधार पर। इन सभी बिट पदों (प्रत्यय) को उनके समकक्ष बाइनरी में 2 2 के स्थान मान में '1' है ।
इसी तरह, समता बिट्स के अन्य मूल्यों का पता लगाएं।
खोजने के लिए इस प्रक्रिया का पालन करें check bits।
बिट 1 , बी 3 , बी 5 , बी 7 और इतने पर मौजूद लोगों की संख्या के आधार पर, सी 1 का मान ज्ञात कीजिए । इन सभी बिट पदों (प्रत्यय) के बराबर बाइनरी में 2 0 के स्थान मान में '1' है ।
बिट 2 , बी 3 , बी 6 , बी 7 और इतने पर मौजूद लोगों की संख्या के आधार पर, सी 2 का मान ज्ञात कीजिए । इन सभी बिट पदों (प्रत्यय) को उनके समकक्ष बाइनरी में 2 1 के स्थान मान में '1' है ।
बिट पदों 4 , बी 5 , बी 6 , बी 7 और इतने पर मौजूद लोगों की संख्या के आधार पर, सी 3 का मान ज्ञात कीजिए । इन सभी बिट पदों (प्रत्यय) को उनके समकक्ष बाइनरी में 2 2 के स्थान मान में '1' है ।
इसी तरह, चेक बिट्स के अन्य मूल्यों का पता लगाएं।
प्राप्त आंकड़ों में चेक बिट्स के बराबर दशमलव बिट स्थिति का मूल्य देता है, जहां त्रुटि मौजूद है। बस उस बिट स्थिति में मौजूद मान को पूरक करें। इसलिए, हम समता बिट्स को हटाने के बाद मूल बाइनरी कोड प्राप्त करेंगे।
उदाहरण 1
आइए हम बाइनरी कोड के लिए हैमिंग कोड ढूंढते हैं, डी 4 डी 3 डी 2 डी 1 = 1000। समता बिट्स पर भी विचार करें।
दिए गए बाइनरी कोड में बिट्स की संख्या n = 4 है।
हम निम्नलिखित गणितीय संबंध का उपयोग करके समता बिट्स की आवश्यक संख्या पा सकते हैं।
$$2^k\geq n+k+1$$
उपर्युक्त गणितीय संबंध में स्थानापन्न, n = 4।
$$\Rightarrow 2^k\geq 4+k+1$$
$$\Rightarrow 2^k\geq 5+k$$
K का न्यूनतम मान जो उपरोक्त संबंध को संतुष्ट करता है 3. इसलिए, हमें 3 समानता बिट्स पी 1 , पी 2 , और पी 3 की आवश्यकता है । इसलिए, हमिंग कोड में बिट्स की संख्या 7 होगी, क्योंकि बाइनरी कोड में 4 बिट्स और 3 पैरिटी बिट्स होते हैं। हमें बाइनरी कोड के समता बिट्स और बिट्स को हैमिंग कोड में नीचे दिखाया गया है।
7-bit Hamming code है $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}=d_{4}d_{3}d_{2}p_{3}d_{1}p_{2}bp_{1}$
बाइनरी कोड के बिट्स को प्रतिस्थापित करके, हेमिंग कोड होगा $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1} = 100p_{3}Op_{2}p_{1}$। अब, हम समता बिट्स का पता लगाएं।
$$p_{1}=b_{7}\oplus b_{5}\oplus b_{3}=1 \oplus 0 \oplus 0=1$$
$$p_{2}=b_{7}\oplus b_{6}\oplus b_{3}=1 \oplus 0 \oplus 0=1$$
$$p_{3}=b_{7}\oplus b_{6}\oplus b_{5}=1 \oplus 0 \oplus 0=1$$
इन समानता बिट्स को प्रतिस्थापित करके, Hamming code होगा $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}= 1001011$।
उदाहरण 2
उपरोक्त उदाहरण में, हमें हैमिंग कोड के रूप में मिला है $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}= 1001011$। अब, जब कोड प्राप्त होता है, तो हम त्रुटि स्थिति का पता लगाते हैं$b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}= 1001111$।
अब, हम चेक बिट्स का पता लगाते हैं।
$$c_{1}=b_{7}\oplus b_{5}\oplus b_{3}\oplus b_{1}=1 \oplus 0 \oplus 1 \oplus1 =1$$
$$c_{2}=b_{7}\oplus b_{6}\oplus b_{3}\oplus b_{2}=1 \oplus 0 \oplus 1 \oplus1 =1$$
$$c_{3}=b_{7}\oplus b_{6}\oplus b_{5}\oplus b_{4}=1 \oplus 0 \oplus 0 \oplus1 =0$$
चेक बिट्स का दशमलव मान प्राप्त किए गए हैमिंग कोड में त्रुटि की स्थिति देता है।
$$c_{3}c_{2}c_{1} = \left ( 011 \right )_{2}=\left ( 3 \right )_{10}$$
इसलिए, हमिंग कोड के तीसरे बिट (बी 3 ) में मौजूद त्रुटि । बस उस बिट में मौजूद मान को पूरक करें और मूल बाइनरी कोड प्राप्त करने के लिए समता बिट्स को हटा दें।
Boolean Algebraएक बीजगणित है, जो द्विआधारी संख्या और द्विआधारी चर से संबंधित है। इसलिए, इसे द्विआधारी बीजगणित या तार्किक बीजगणित भी कहा जाता है। जॉर्ज बोले नाम के एक गणितज्ञ ने 1854 में इस बीजगणित को विकसित किया था। इस बीजगणित में प्रयुक्त चर को बुलियन चर भी कहा जाता है।
लॉजिक 'हाई' के अनुरूप वोल्टेज की श्रेणी को '1' के साथ दर्शाया गया है और लॉजिक के लिए वोल्टेज की रेंज को 'लो' से दर्शाया गया है।
बूलियन बीजगणित के पोस्टऑफिस और मूल नियम
इस खंड में, हम बूलियन पोस्टुलेट्स और मूल कानूनों के बारे में चर्चा करते हैं जो बूलियन बीजगणित में उपयोग किए जाते हैं। ये बूलियन कार्यों को कम करने में उपयोगी होते हैं।
बुलियन पोस्टुलेट करता है
बाइनरी नंबर 0 और 1, बूलियन चर (एक्स) और इसके पूरक (एक्स ') पर विचार करें। या तो बूलियन चर या इसके पूरक के रूप में जाना जाता हैliteral। चार संभवlogical OR इन शाब्दिक और द्विआधारी संख्याओं के बीच संचालन नीचे दिखाया गया है।
x + 0 = x
x + 1 = 1
x + x = x
x + x '= 1
इसी तरह, चार संभव logical AND उन शाब्दिक और द्विआधारी संख्याओं के बीच संचालन नीचे दिखाया गया है।
x.1 = x
x.0 = 0
xx = x
x.x '= 0
ये साधारण बूलियन आसन हैं। हम बूलियन वैरिएबल को '0' या '1' के साथ बदलकर, इन पोस्टुलेट्स को आसानी से सत्यापित कर सकते हैं।
Note- किसी बूलियन वैरिएबल के सप्लीमेंट की वैल्यू वैरिएबल के बराबर ही होती है। यानी, (x ')' = x।
बूलियन बीजगणित के मूल नियम
बूलियन बीजगणित के तीन बुनियादी नियम निम्नलिखित हैं।
- विनिमेय कानून
- सहयोगी कानून
- वितरण संबंधी कानून
विनिमेय कानून
यदि दो बूलियन चर का कोई तार्किक संचालन उन दो चर के आदेश के बावजूद समान परिणाम देता है, तो उस तार्किक संचालन को कहा जाता है Commutative। तार्किक और तार्किक और दो बूलियन चर x & y के संचालन नीचे दिखाए गए हैं
x + y = y + x
xy = yx
प्रतीक '+' तार्किक या संचालन को इंगित करता है। इसी तरह, प्रतीक '।' तार्किक और ऑपरेशन इंगित करता है और यह प्रतिनिधित्व करने के लिए वैकल्पिक है। लॉजिकल लॉ लॉजिकल या लॉजिकल एंड ऑपरेशंस के लिए पालन करता है।
सहयोगी कानून
यदि किसी भी दो बूलियन चर का तार्किक संचालन पहले किया जाता है और फिर शेष चर के साथ एक ही ऑपरेशन किया जाता है, तो उस तार्किक ऑपरेशन को कहा जाता है Associative। तार्किक और तार्किक और तीन बूलियन चर x, y और z के संचालन को नीचे दिखाया गया है।
x + (y + z) = (x + y) + z
x। (yz) = (xy) .z
साहचर्य कानून तार्किक या तार्किक और संचालन के लिए पालन करता है।
वितरण संबंधी कानून
यदि बूलियन फ़ंक्शन में मौजूद सभी शर्तों को कोई तार्किक ऑपरेशन वितरित किया जा सकता है, तो उस तार्किक ऑपरेशन को कहा जाता है Distributive। तार्किक और तार्किक और तीन बूलियन चर x, y & z के संचालन के वितरण को नीचे दिखाया गया है।
x। (y + z) = xy + xz
x + (yz) = (x + y)। (x + z)
वितरण कानून तार्किक या तार्किक और संचालन के लिए पालन करता है।
ये बूलियन बीजगणित के मूल नियम हैं। हम इन कानूनों को आसानी से सत्यापित कर सकते हैं, बूलियन चर को '0' या '1' के साथ प्रतिस्थापित करके।
बूलियन बीजगणित के सिद्धांत
निम्नलिखित दो प्रमेयों का उपयोग बुलियन बीजगणित में किया जाता है।
- द्वंद्व प्रमेय
- डेमोरोन की प्रमेय
द्वंद्व सिद्धांत
यह प्रमेय बताता है कि dualबूलियन फ़ंक्शन को तार्किक या ऑपरेटर को तार्किक या ऑपरेटर और शून्य के साथ इंटरचेंज करके प्राप्त किया जाता है। प्रत्येक बूलियन फ़ंक्शन के लिए, एक संगत दोहरी फ़ंक्शन होगा।
आइए हम बूलियन समीकरण (संबंध) बनाते हैं, जिसकी चर्चा हमने बूलियन के अनुभागों और बुनियादी कानूनों के दो समूहों में की। निम्न तालिका इन दो समूहों को दिखाती है।
| समूह 1 | समूह 2 |
|---|---|
| x + 0 = x | x.1 = x |
| x + 1 = 1 | x.0 = 0 |
| x + x = x | xx = x |
| x + x '= 1 | x.x '= 0 |
| x + y = y + x | xy = yx |
| x + (y + z) = (x + y) + z | x। (yz) = (xy) .z |
| x। (y + z) = xy + xz | x + (yz) = (x + y)। (x + z) |
प्रत्येक पंक्ति में, दो बूलियन समीकरण होते हैं और वे एक दूसरे के लिए दोहरे होते हैं। हम ग्रुप 1 और ग्रुप 2 के इन सभी बूलियन समीकरणों का सत्यापन द्वैत प्रमेय का उपयोग करके कर सकते हैं।
डेमैगन के प्रमेय
यह प्रमेय खोजने में उपयोगी है complement of Boolean function। यह बताता है कि तार्किक या कम से कम दो बुलियन चर का पूरक तार्किक और प्रत्येक पूरक चर के बराबर है।
2 बूलियन चर x और y के साथ DeMorgan के प्रमेय का प्रतिनिधित्व किया जा सकता है
(x + y) '= x'y'
उपरोक्त बूलियन फ़ंक्शन का दोहरी है
(xy) '= x' + y '
इसलिए, दो बूलियन चर के तार्किक और के पूरक तार्किक या प्रत्येक पूरक चर के बराबर है। इसी तरह, हम 2 से अधिक बूलियन चर के लिए डेमोरोन के प्रमेय को भी लागू कर सकते हैं।
बूलियन फ़ंक्शंस का सरलीकरण
अब तक, हमने बूलियन बीजगणित के पदों, मूल कानूनों और प्रमेयों पर चर्चा की। अब, हम बूलियन कार्यों को सरल बनाते हैं।
उदाहरण 1
हमें करने दो simplify बूलियन फ़ंक्शन, f = p'qr + pq'r + pqr '+ pqr
हम इस फ़ंक्शन को दो तरीकों से सरल कर सकते हैं।
Method 1
बूलियन फ़ंक्शन को देखते हुए, f = p'qr + pq'r + pqr '+ pqr।
Step 1- पहले और दूसरे शब्दों में r सामान्य और तीसरे और चौथे शब्दों में pq आम है। इसलिए, उपयोग करके सामान्य शब्द लेंDistributive law।
⇒ f = (p'q + pq ') r + pq (r' + r)
Step 2- पहले कोष्ठक में मौजूद शर्तों को पूर्व या ऑपरेशन के लिए सरल बनाया जा सकता है। दूसरे कोष्ठक में मौजूद शब्दों का उपयोग करके '1' को सरल बनाया जा सकता हैBoolean postulate
⇒ f = (p )q) r + pq (1)
Step 3- पहले कार्यकाल को और सरल नहीं किया जा सकता है। लेकिन, दूसरे पद का उपयोग करके pq को सरल बनाया जा सकता हैBoolean postulate।
⇒ f = (p )q) r + pq
इसलिए, सरलीकृत बूलियन फ़ंक्शन है f = (p⊕q)r + pq
Method 2
बूलियन फ़ंक्शन को देखते हुए, f = p'qr + pq'r + pqr '+ pqr।
Step 1 - का उपयोग करें Boolean postulate, x + x = x। इसका मतलब है, किसी भी बूलियन चर 'एन' समय के साथ लॉजिकल या ऑपरेशन एक ही चर के बराबर होगा। तो, हम अंतिम शब्द pqr को दो बार लिख सकते हैं।
⇒ f = p'qr + pq'r + pqr '+ pqr + pqr + pqr
Step 2 - उपयोग करें Distributive law1 सेंट और 4 वें शब्दों के लिए, 2 एन डी और 5 वीं शर्तें, 3 आरडी और 6 वें शब्दों के लिए।
⇒ f = qr (p '+ p) + pr (q' + q) + pq (r '+ r)
Step 3 - उपयोग करें Boolean postulate, x + x '= 1 प्रत्येक कोष्ठक में मौजूद शब्दों को सरल बनाने के लिए।
⇒ f = qr (1) + pr (1) + pq (1)
Step 4 - उपयोग करें Boolean postulate, x.1 = x उपरोक्त तीन शब्दों को सरल बनाने के लिए।
⇒ f = qr + pr + pq
⇒ f = pq + qr + pr
इसलिए, सरलीकृत बूलियन फ़ंक्शन है f = pq + qr + pr।
इसलिए, हमें प्रत्येक विधि में दिए गए बूलियन फ़ंक्शन को सरल बनाने के बाद दो अलग-अलग बूलियन फ़ंक्शन मिले। कार्यात्मक रूप से, दो बूलियन फ़ंक्शन समान हैं। इसलिए, आवश्यकता के आधार पर, हम उन दो बूलियन कार्यों में से एक चुन सकते हैं।
उदाहरण 2
हमें खोजने दो complement बूलियन फ़ंक्शन का, f = p'q + pq '।
बूलियन फ़ंक्शन का पूरक f '= (p'q + pq') 'है।
Step 1 - DeMorgan के प्रमेय, (x + y) '= x'y' का उपयोग करें।
⇒ f '= (p'q)'। (pq ')'
Step 2 - DeMorgan के प्रमेय का प्रयोग करें, (xy) '= x' + y '
⇒ f '= {(p') '+ q'}। {p '+ (q') '}
Step3 - बूलियन पोस्टुलेट का उपयोग करें, (x ')' = x।
⇒ f '= {p + q'}। {p '+ q}
⇒ f '= pp' + pq + p'q '+ qq'
Step 4 - बूलियन पोस्टुलेट का उपयोग करें, xx '= 0।
⇒ f = 0 + pq + p'q '+ 0
⇒ f = pq + p'q '
इसलिए complement बूलियन फ़ंक्शन, p'q + pq 'है pq + p’q’।
हम तार्किक और ऑपरेशन के साथ दो चर x और y को मिलाकर चार बूलियन उत्पाद शब्द प्राप्त करेंगे। इन बूलियन उत्पाद की शर्तों को कहा जाता हैmin terms या standard product terms। न्यूनतम शर्तें x'y ', x'y, xy' और xy हैं।
इसी तरह, हम तार्किक या ऑपरेशन के साथ दो चर x और y को मिलाकर चार बुलियन योग शब्द प्राप्त करेंगे। इन बूलियन राशि शर्तों के रूप में कहा जाता हैMax terms या standard sum terms। अधिकतम शब्द x + y, x + y ', x' + y और x '+ y' हैं।
निम्न तालिका 2 चर के लिए न्यूनतम शर्तों और अधिकतम शर्तों का प्रतिनिधित्व दर्शाती है।
| एक्स | y | न्यूनतम शर्तें | अधिकतम शर्तें |
|---|---|---|---|
| 0 | 0 | मी 0 = x'y ' | M 0 = x + y |
| 0 | 1 | m 1 = x'y | M 1 = x + y ' |
| 1 | 0 | एम 2 = xy ' | एम 2 = एक्स '+ वाई |
| 1 | 1 | म 3 = xy | M 3 = x '+ y' |
यदि द्विआधारी चर '0' है, तो इसे मिनिम टर्म में वेरिएबल के पूरक के रूप में और मैक्स टर्म में स्वयं वेरिएबल के रूप में दर्शाया जाता है। इसी प्रकार, यदि द्विआधारी चर '1 ’है, तो इसे मैक्स शब्द में चर के पूरक के रूप में और शून्य अवधि में स्वयं चर के रूप में दर्शाया जाता है।
उपरोक्त तालिका से, हम आसानी से देख सकते हैं कि न्यूनतम शर्तें और अधिकतम शर्तें एक दूसरे के पूरक हैं। यदि 'एन' बुलियन चर हैं, तो 2 एन मिनट की शर्तें और 2 एन मैक्स शब्द होंगे।
Canonical SoP और PoS रूपों
एक सत्य तालिका में इनपुट और आउटपुट (एस) का एक सेट होता है। यदि 'एन' इनपुट चर हैं, तो शून्य और लोगों के साथ 2 एन संभव संयोजन होंगे। तो प्रत्येक आउटपुट चर का मूल्य इनपुट चर के संयोजन पर निर्भर करता है। तो, प्रत्येक आउटपुट चर में इनपुट चर के कुछ संयोजन के लिए '1' और इनपुट चर के कुछ अन्य संयोजन के लिए '0' होगा।
इसलिए, हम प्रत्येक आउटपुट चर को दो तरीकों से अनुसरण कर सकते हैं।
- विहित सोप रूप
- विहित PoS रूप
विहित सोप रूप
Canonical SoP फॉर्म का मतलब होता है Canonical Sum of Products फॉर्म। इस रूप में, प्रत्येक उत्पाद शब्द में सभी शाब्दिक शब्द होते हैं। तो, ये उत्पाद शब्द मिनिमम टर्म के अलावा और कुछ नहीं हैं। इसलिए, विहित SoP रूप को भी कहा जाता हैsum of min terms प्रपत्र।
सबसे पहले, उन मिनिमम टर्म्स की पहचान करें, जिनके लिए आउटपुट वेरिएबल एक है और फिर उस आउटपुट वेरिएबल के अनुरूप बूलियन एक्सप्रेशन (फंक्शन) प्राप्त करने के लिए उन OR टर्म्स की तार्किक या कर सकते हैं। यह बुलियन फंक्शन मिनिमम टर्म के योग के रूप में होगा।
अन्य आउटपुट चर के लिए भी यही प्रक्रिया अपनाएं, यदि एक से अधिक आउटपुट चर हैं।
उदाहरण
निम्नलिखित को धयान मे रखते हुए truth table।
| इनपुट | उत्पादन | ||
|---|---|---|---|
| p | q | r | f |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
यहाँ, इनपुट के चार संयोजनों के लिए आउटपुट (f) '1' है। संबंधित न्यूनतम शर्तें p'qr, pq'r, pqr ', pqr हैं। तार्किक या इन चार मिनट की शर्तों को करके, हम आउटपुट (च) का बूलियन फ़ंक्शन प्राप्त करेंगे।
इसलिए, आउटपुट का बूलियन फ़ंक्शन है, f = p'qr + pq'r + pqr '+ pqr। यह हैcanonical SoP formआउटपुट का, एफ। हम भी दो संकेतन के बाद इस समारोह का प्रतिनिधित्व कर सकते हैं।
$$f = m_{3}+m_{5}+m_{6}+m_{7}$$
$$f = \sum m\left ( 3,5,6,7 \right )$$
एक समीकरण में, हमने संबंधित न्यूनतम शर्तों के योग के रूप में फ़ंक्शन का प्रतिनिधित्व किया। अन्य समीकरणों में, हमने उन मिनटों के योग के लिए प्रतीक का उपयोग किया।
विहित PoS रूप
Canonical PoS फॉर्म का मतलब होता है Canonical Product of Sums का फॉर्म। इस रूप में, प्रत्येक योग शब्द में सभी शाब्दिक शब्द होते हैं। तो, ये शब्द शर्तें और कुछ नहीं बल्कि मैक्स शब्द हैं। इसलिए, विहित PoS रूप को भी कहा जाता हैproduct of Max terms प्रपत्र।
सबसे पहले, अधिकतम शब्दों की पहचान करें जिसके लिए, आउटपुट चर शून्य है और फिर उस आउटपुट चर के अनुरूप बूलियन अभिव्यक्ति (फ़ंक्शन) प्राप्त करने के लिए उन मैक्स शब्दों की तार्किक और करें। यह बूलियन फ़ंक्शन मैक्स शर्तों के उत्पाद के रूप में होगा।
अन्य आउटपुट चर के लिए भी यही प्रक्रिया अपनाएं, यदि एक से अधिक आउटपुट चर हैं।
Example
पिछले उदाहरण की समान सत्य तालिका पर विचार करें। यहाँ, इनपुट के चार संयोजनों के लिए आउटपुट (f) '0' है। संबंधित मैक्स पद p + q + r, p + q + r ', p + q' + r, p '+ q + r हैं। तार्किक और इन चार अधिकतम शब्दों को करने से, हम बूलियन फ़ंक्शन ऑफ़ आउटपुट (f) प्राप्त करेंगे।
इसलिए, आउटपुट का बूलियन फ़ंक्शन है, f = (p + q + r)। (p + q + r ')। (p + q' + r)। (p '+ q + r)। यह हैcanonical PoS formआउटपुट का, एफ। हम भी दो संकेतन के बाद इस समारोह का प्रतिनिधित्व कर सकते हैं।
$$f=M_{0}.M_{1}.M_{2}.M_{4}$$
$$f=\prod M\left ( 0,1,2,4 \right )$$
एक समीकरण में, हमने संबंधित मैक्स शब्दों के उत्पाद के रूप में फ़ंक्शन का प्रतिनिधित्व किया। अन्य समीकरण में, हमने उन अधिकतम शब्दों के गुणन के लिए प्रतीक का उपयोग किया।
बूलियन फ़ंक्शन, f = (p + q + r)। (p + q + r ')। (p + q' + r)। (p '+ q + r) बूलियन फ़ंक्शन का दोहरी है, f = p'qr + pq'r + pqr '+ pqr।
इसलिए, विहित SoP और विहित PoS दोनों रूप हैं Dualएक दूसरे को। कार्यात्मक रूप से, ये दो रूप समान हैं। आवश्यकता के आधार पर, हम इन दो रूपों में से एक का उपयोग कर सकते हैं।
मानक SoP और PoS रूप
हमने बूलियन आउटपुट (एस) का प्रतिनिधित्व करने के दो विहित रूपों पर चर्चा की। इसी तरह, बूलियन आउटपुट (एस) का प्रतिनिधित्व करने के दो मानक रूप हैं। ये विहित रूपों का सरलीकृत संस्करण हैं।
- मानक SoP रूप
- मानक PoS रूप
हम बाद के अध्यायों में तर्क फाटकों के बारे में चर्चा करेंगे। मुख्यadvantageमानक रूपों में तर्क गेट्स पर लगाए गए इनपुट की संख्या को कम से कम किया जा सकता है। कभी-कभी, आवश्यक तर्क गेट्स की कुल संख्या में कमी होगी।
मानक SoP रूप
मानक SoP फॉर्म का मतलब है Standard Sum of Productsप्रपत्र। इस रूप में, प्रत्येक उत्पाद शब्द में सभी शाब्दिक शब्द नहीं होते हैं। तो, उत्पाद की शर्तें न्यूनतम शर्तें हो सकती हैं या नहीं भी हो सकती हैं। इसलिए, मानक SoP फॉर्म विहित SoP फॉर्म का सरलीकृत रूप है।
हमें दो चरणों में आउटपुट वेरिएबल का स्टैंडर्ड सोप मिलेगा।
- आउटपुट चर का विहित SoP रूप प्राप्त करें
- उपरोक्त बूलियन फ़ंक्शन को सरल करें, जो विहित SoP रूप में है।
अन्य आउटपुट चर के लिए भी यही प्रक्रिया अपनाएं, यदि एक से अधिक आउटपुट चर हैं। कभी-कभी, विहित SoP रूप को सरल करना संभव नहीं होता है। उस स्थिति में, विहित और मानक SoP दोनों रूप समान हैं।
Example
निम्नलिखित बूलियन फ़ंक्शन को स्टैंडर्ड SoP फॉर्म में बदलें।
f = p'qr + pq'r + pqr '+ pqr
दिए गए बूलियन फ़ंक्शन विहित SoP रूप में है। अब, हमें इस बूलियन फ़ंक्शन को सरल करना होगा ताकि मानक एसओपी फॉर्म प्राप्त हो सके।
Step 1 - का उपयोग करें Boolean postulate, x + x = x। इसका मतलब है, किसी भी बूलियन चर 'एन' समय के साथ लॉजिकल या ऑपरेशन एक ही चर के बराबर होगा। तो, हम अंतिम शब्द pqr को दो बार लिख सकते हैं।
⇒ f = p'qr + pq'r + pqr '+ pqr + pqr + pqr
Step 2 - उपयोग करें Distributive law1 सेंट और 4 वें शब्दों के लिए, 2 एन डी और 5 वीं शर्तें, 3 आरडी और 6 वें शब्दों के लिए।
⇒ f = qr (p '+ p) + pr (q' + q) + pq (r '+ r)
Step 3 - उपयोग करें Boolean postulate, x + x '= 1 प्रत्येक कोष्ठक में मौजूद शब्दों को सरल बनाने के लिए।
⇒ f = qr (1) + pr (1) + pq (1)
Step 4 - उपयोग करें Boolean postulate, x.1 = x तीन शब्दों के ऊपर सरलीकरण के लिए।
⇒ f = qr + pr + pq
⇒ f = pq + qr + pr
यह सरलीकृत बूलियन फ़ंक्शन है। इसलिएstandard SoP form दिए गए विहित SoP रूप के अनुरूप है f = pq + qr + pr
मानक PoS रूप
मानक PoS फॉर्म का मतलब है Standard Product of Sumsप्रपत्र। इस रूप में, प्रत्येक योग शब्द में सभी शाब्दिक शब्द नहीं होते हैं। तो, अधिकतम शर्तें अधिकतम शर्तें हो सकती हैं या नहीं। इसलिए, मानक PoS रूप विहित PoS रूप का सरलीकृत रूप है।
हमें दो चरणों में आउटपुट चर का मानक पीओएस फॉर्म मिलेगा।
- आउटपुट चर का विहित PoS रूप प्राप्त करें
- उपरोक्त बूलियन फ़ंक्शन को सरल करें, जो विहित PoS रूप में है।
अन्य आउटपुट चर के लिए भी यही प्रक्रिया अपनाएं, यदि एक से अधिक आउटपुट चर हैं। कभी-कभी, विहित PoS रूप को सरल करना संभव नहीं होता है। उस मामले में, दोनों विहित और मानक PoS रूप समान हैं।
Example
निम्नलिखित बूलियन फ़ंक्शन को मानक PoS रूप में परिवर्तित करें।
f = (p + q + r)। (p + q + r ')। (p + q' + r) (p '+ q + r)
दिए गए बूलियन कार्य विहित PoS रूप में हैं। अब, मानक पीओएस फॉर्म प्राप्त करने के लिए हमें इस बूलियन फ़ंक्शन को सरल करना होगा।
Step 1 - का उपयोग करें Boolean postulate, xx = x। इसका मतलब है, किसी भी बूलियन चर 'एन' समय के साथ तार्किक और ऑपरेशन एक ही चर के बराबर होगा। इसलिए, हम पहले शब्द p + q + r को दो बार लिख सकते हैं।
⇒ f = (p + q + r)। (p + q + r)। (p + q + r)। (p + q + r ')। (p + q' + r)। (p '+ q) + आर)
Step 2 - उपयोग करें Distributive law,x + (yz) = (x + y)। (x + z) 1 सेंट और 4 वें कोष्ठक, 2 nd और 5 वें कोष्ठक, 3 rd और 6 वें लघुकोष्ठक के लिए।
⇒ f = (p + q + rr ')। (p + r + qq')। (q + r + pp)
Step 3 - उपयोग करें Boolean postulate, x.x '= 0 प्रत्येक कोष्ठक में मौजूद शब्दों को सरल बनाने के लिए।
⇒ f = (p + q + 0)। (p + r + 0)। (q + r + 0)
Step 4 - उपयोग करें Boolean postulate, प्रत्येक कोष्ठक में मौजूद शब्दों को सरल बनाने के लिए x + 0 = x
⇒ f = (p + q)। (p + r)। (q + r)
⇒ f = (p + q)। (q + r)। (p + r)
यह सरलीकृत बूलियन फ़ंक्शन है। इसलिएstandard PoS form दिए गए विहित PoS रूप के अनुरूप है f = (p + q).(q + r).(p + r)। यह हैdual बूलियन फ़ंक्शन का, f = pq + qr + pr।
इसलिए, Standard SoP और Standard PoS दोनों एक दूसरे के लिए दोहरी हैं।
पिछले अध्यायों में, हमने बूलियन पदों और प्रमेयों का उपयोग करके बूलियन कार्यों को सरल बनाया है। यह एक समय लेने वाली प्रक्रिया है और हमें प्रत्येक चरण के बाद सरलीकृत अभिव्यक्तियों को फिर से लिखना होगा।
इस कठिनाई को दूर करने के लिए, Karnaughएक आसान तरीके से बूलियन कार्यों के सरलीकरण के लिए एक विधि शुरू की। इस विधि को कर्णघ मानचित्र विधि या के-मानचित्र विधि के रूप में जाना जाता है। यह एक ग्राफिकल विधि है, जिसमें 'एन' वेरिएबल्स के लिए 2 एन सेल होते हैं । आसन्न कोशिकाएं केवल एकल बिट स्थिति में भिन्न होती हैं।
2 से 5 चर के लिए कश्मीर मैप्स
K-Map विधि 2 चरों के 5 कार्यों के बूलियन कार्यों को कम करने के लिए सबसे उपयुक्त है। अब, एक-एक करके के-मैप्स के बारे में 2 से 5 वेरिएबल्स के बारे में चर्चा करते हैं।
2 चर K- नक्शा
2 चर के-मानचित्र में कोशिकाओं की संख्या चार है, क्योंकि चर की संख्या दो है। निम्नलिखित आंकड़ा दिखाता है2 variable K-Map।
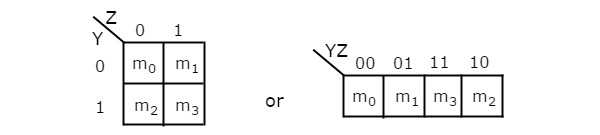
4 आसन्न न्यूनतम शर्तों को समूहीकृत करने की केवल एक संभावना है।
2 आसन्न न्यूनतम पदों को समूहीकृत करने के संभावित संयोजन {(m 0 , m 1 ), (m 2 , m 3 ), (m 0 , m 2 ) और (m 1 , m 3 )} हैं।
3 चर K- नक्शा
3 चर K- मानचित्र में कोशिकाओं की संख्या आठ है, क्योंकि चर की संख्या तीन है। निम्नलिखित आंकड़ा दिखाता है3 variable K-Map।
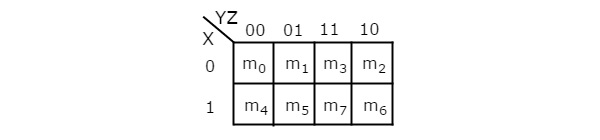
8 आसन्न न्यूनतम शर्तों को समूहीकृत करने की केवल एक संभावना है।
4 आसन्न न्यूनतम शर्तों को समूहीकृत करने के संभावित संयोजन हैं {(m 0 , m 1 , m 3 , m 2 ), (m 4 , m 5 , m 7 , m 6 ), (m 0 , m 1 , m 4 , m 5 ), (एम 1 , एम 3 , एम 5 , एम 7 ), (एम 3 , एम 2 , एम 7 , एम 6 ) और (एम 2 , एम 0 , एम 6 , एम 4 )}।
2 आसन्न न्यूनतम पदों को समूहीकृत करने के संभावित संयोजन {(m 0 , m 1 ), (m 1 , m 3 ), (m 3 , m 2 ), (m 2 , m 0 ), (m 4 , m 5 ) हैं , (एम 5 , एम 7 ), (एम 7 , एम 6 ), (एम 6 , एम 4 ), (एम 0 , एम 4 ), (एम 1 , एम 5 ), (एम 3 , एम 7 ) और ( एम 2 , एम 6 )}।
यदि x = 0 है, तो 3 चर K- मानचित्र 2 चर K- मानचित्र बन जाता है।
4 चर K- नक्शा
4 चर K- मानचित्र में कोशिकाओं की संख्या सोलह है, क्योंकि चर की संख्या चार है। निम्नलिखित आंकड़ा दिखाता है4 variable K-Map।
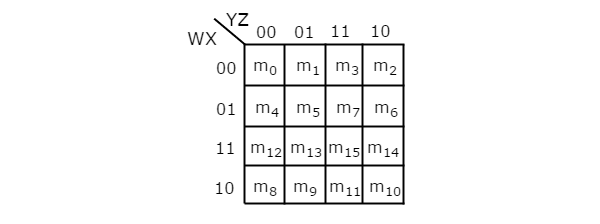
16 आसन्न न्यूनतम शर्तों को समूहीकृत करने की केवल एक संभावना है।
R 1 , R 2 , R 3 और R 4 को क्रमशः पहली पंक्ति, दूसरी पंक्ति, तीसरी पंक्ति और चौथी पंक्ति की न्यूनतम शर्तों का प्रतिनिधित्व करता है। इसी तरह, सी 1 , सी 2 , सी 3 और सी 4 क्रमशः पहले कॉलम, दूसरे कॉलम, तीसरे कॉलम और चौथे कॉलम की न्यूनतम शर्तों का प्रतिनिधित्व करते हैं। 8 आसन्न न्यूनतम शर्तों के समूहन के संभावित संयोजन {(R 1 , R 2 ), (R 2 , R 3 ), (R 3 , R 4 ), (R 4 , R 1 ), (C 1 , C 2 ) हैं। , (C 2 , C 3 ), (C 3 , C 4 ), (C 4 , C 1 )}।
यदि w = 0 है, तो 4 चर K- मानचित्र 3 चर K- मानचित्र बन जाता है।
5 चर K- नक्शा
5 चर के-मानचित्र में कोशिकाओं की संख्या बत्तीस है, चूंकि चर की संख्या 5. है। निम्नलिखित आंकड़ा दिखाता है 5 variable K-Map।

32 आसन्न न्यूनतम शर्तों को समूहीकृत करने की केवल एक संभावना है।
16 आसन्न न्यूनतम शर्तों को समूहीकृत करने की दो संभावनाएँ हैं। अर्थात, मी 0 से एम 15 और एम 16 से एम 31 तक न्यूनतम अवधि ।
यदि v = 0 है, तो 5 चर K- मानचित्र 4 चर K- मानचित्र बन जाता है।
उपर्युक्त सभी के-नक्शों में, हमने विशेष रूप से न्यूनतम शर्तों के अंकन का उपयोग किया है। इसी तरह, आप विशेष रूप से अधिकतम शर्तों के अंकन का उपयोग कर सकते हैं।
के-मैप्स का उपयोग करके बूलियन फ़ंक्शंस का न्यूनतमकरण
यदि हम इनपुट के संयोजन पर विचार करते हैं जिसके लिए बूलियन फ़ंक्शन '1' है, तो हमें बूलियन फ़ंक्शन मिलेगा, जो कि standard sum of products K-map को सरल बनाने के बाद प्रपत्र।
इसी तरह, अगर हम उन इनपुटों के संयोजन पर विचार करते हैं जिनके लिए बूलियन फ़ंक्शन '0' है, तो हम बूलियन फ़ंक्शन को प्राप्त करेंगे, जो कि में है standard product of sums K-map को सरल बनाने के बाद प्रपत्र।
इनका पालन करें rules for simplifying K-maps उत्पादों के मानक योग प्राप्त करने के लिए।
बूलियन फ़ंक्शन में मौजूद चर की संख्या के आधार पर संबंधित के-मानचित्र का चयन करें।
यदि बूलियन फ़ंक्शन को मिनिमम टर्म फॉर्म के रूप में दिया जाता है, तो उन्हें के-मैप में संबंधित मिनिमम सेल में रखें। यदि बूलियन फ़ंक्शन को उत्पादों के योग के रूप में दिया जाता है, तो उन्हें के-मैप के सभी संभावित कक्षों में रखें, जिसके लिए दिए गए उत्पाद की शर्तें मान्य हैं।
आस-पास के लोगों की अधिकतम संख्या को समूहीकृत करने की संभावनाओं की जाँच करें। यह दो की शक्तियां होनी चाहिए। दो की उच्चतम शक्ति से शुरू करें और दो की अधिकतम शक्ति तक। उच्चतम शक्ति K- मानचित्र में माने जाने वाले चरों की संख्या के बराबर है और सबसे कम शक्ति शून्य है।
प्रत्येक समूह या तो एक शाब्दिक या एक उत्पाद शब्द देगा। इसे यह भी कहा जाता हैprime implicant। प्रमुख अधिपति कहा जाता हैessential prime implicant, अगर कम से कम एकल '1' को किसी अन्य समूह के साथ कवर नहीं किया जाता है, लेकिन केवल उस समूहीकरण को कवर किया जाता है।
सभी प्रमुख इम्प्लिकेंट्स और आवश्यक प्राइम इम्प्लिकेंट्स पर ध्यान दें। सरलीकृत बूलियन फ़ंक्शन में सभी आवश्यक प्राइम इम्प्लिकेंट्स और केवल आवश्यक प्राइम इम्प्लिकेंट्स होते हैं।
Note 1 - यदि आउटपुट इनपुट के कुछ संयोजन के लिए परिभाषित नहीं हैं, तो उन आउटपुट मानों के साथ प्रतिनिधित्व किया जाएगा don’t care symbol ‘x’। इसका मतलब है कि, हम उन्हें '0' या '1' मान सकते हैं।
Note 2- अगर देखभाल की शर्तें भी मौजूद नहीं हैं, तो के-मैप की संबंधित कोशिकाओं में 'x' को न रखें। केवल 'x' की परवाह न करें, जो आस-पास के लोगों की अधिकतम संख्या के लिए सहायक हो। उन मामलों में, '1' के रूप में परवाह न करें।
उदाहरण
हमें करने दो simplify निम्नलिखित बूलियन फ़ंक्शन, f(W, X, Y, Z)= WX’Y’ + WY + W’YZ’ K- मानचित्र का उपयोग करना।
दिए गए बूलियन फ़ंक्शन उत्पादों के योग में हैं। यह 4 चर डब्ल्यू, एक्स, वाई एंड जेड है। इसलिए, हमें इसकी आवश्यकता है4 variable K-map। 4 variable K-map दिए गए उत्पाद की शर्तों से संबंधित लोगों को निम्नलिखित आकृति में दिखाया गया है।
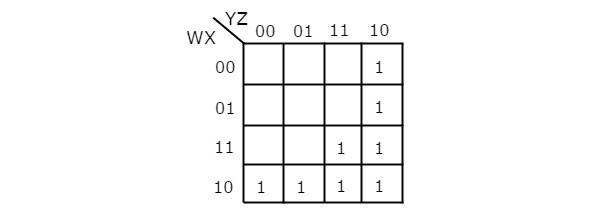
यहां, 1s को K-map की निम्नलिखित कोशिकाओं में रखा गया है।
कोशिकाएं, जो पंक्ति 4 और स्तंभ 1 और 2 के प्रतिच्छेदन के लिए सामान्य हैं, उत्पाद अवधि के अनुरूप हैं, WX’Y’।
कोशिकाएं, जो पंक्तियों 3 और 4 के चौराहे पर आम हैं और कॉलम 3 और 4 उत्पाद अवधि के अनुरूप हैं, WY।
कोशिकाएं, जो पंक्तियों 1 और 2 और स्तंभ 4 के प्रतिच्छेदन के लिए सामान्य हैं, उत्पाद अवधि के अनुरूप हैं, W’YZ’।
16 निकटवर्ती या 8 आसन्न लोगों के समूह की कोई संभावना नहीं है। 4 आसन्न लोगों के समूह की तीन संभावनाएं हैं। इन तीन समूहों के बाद, कोई भी एक समूह नहीं बचा है। इसलिए, हमें 2 आसन्न लोगों के समूहन के लिए जाँच करने की आवश्यकता नहीं है। 4 variable K-map इन तीनों के साथ groupings निम्नलिखित आकृति में दिखाया गया है।

यहां, हमें तीन प्रमुख प्रत्यारोपण WX ', WY & YZ' मिले। ये सभी प्राइम इंप्लांट्स हैंessential निम्नलिखित कारणों से।
दो वाले (m8 & m9)चौथी पंक्ति के समूहन को किसी अन्य समूह द्वारा कवर नहीं किया जाता है। केवल चौथी पंक्ति समूहन में उन दो को शामिल किया गया है।
अविवाहित (m15)चौकोर आकार के समूह को किसी अन्य समूह द्वारा कवर नहीं किया जाता है। केवल चौकोर आकार समूह समूहीकरण को कवर करता है।
दो वाले (m2 & m6)चौथे स्तंभ समूह को किसी अन्य समूह द्वारा कवर नहीं किया गया है। केवल चौथा स्तंभ समूह उन दो को कवर करता है।
इसलिए simplified Boolean function है
f = WX’ + WY + YZ’
इनका पालन करें rules for simplifying K-maps रकम के मानक उत्पाद प्राप्त करने के लिए।
बूलियन फ़ंक्शन में मौजूद चर की संख्या के आधार पर संबंधित के-मानचित्र का चयन करें।
यदि बूलियन फ़ंक्शन को मैक्स के रूप के उत्पाद के रूप में दिया जाता है, तो शून्य को के-मैप में संबंधित मैक्स टर्म कोशिकाओं पर रखें। यदि बूलियन फ़ंक्शन को रकम फॉर्म के उत्पाद के रूप में दिया जाता है, तो शून्य को के-मैप के सभी संभावित कोशिकाओं में रखें, जिसके लिए दिए गए योग शब्द मान्य हैं।
आसन्न शून्य की अधिकतम संख्या को समूहीकृत करने की संभावनाओं की जाँच करें। यह दो की शक्तियां होनी चाहिए। दो की उच्चतम शक्ति से शुरू करें और दो की अधिकतम शक्ति तक। उच्चतम शक्ति K- मानचित्र में माने जाने वाले चरों की संख्या के बराबर है और सबसे कम शक्ति शून्य है।
प्रत्येक समूह या तो एक शाब्दिक या एक योग शब्द देगा। इसे यह भी कहा जाता हैprime implicant। प्रमुख अधिपति कहा जाता हैessential prime implicant, अगर कम से कम एकल '0' को किसी अन्य समूह के साथ कवर नहीं किया जाता है, लेकिन केवल उस समूहीकरण को कवर किया जाता है।
सभी प्रमुख इम्प्लिकेंट्स और आवश्यक प्राइम इम्प्लिकेंट्स पर ध्यान दें। सरलीकृत बूलियन फ़ंक्शन में सभी आवश्यक प्राइम इम्प्लिकेंट्स और केवल आवश्यक प्राइम इम्प्लिकेंट्स होते हैं।
Note- अगर देखभाल की शर्तें भी मौजूद नहीं हैं, तो के-मैप की संबंधित कोशिकाओं में 'x' को न रखें। केवल 'x' की परवाह न करें, जो अधिकतम संख्या में आसन्न शून्य को समूहीकृत करने में सहायक हो। उन मामलों में, परवाह न करें मान को '0' के रूप में देखें।
उदाहरण
हमें करने दो simplify निम्नलिखित बूलियन फ़ंक्शन, $f\left ( X,Y,Z \right )=\prod M\left ( 0,1,2,4 \right )$ K- मानचित्र का उपयोग करना।
दिए गए बूलियन फ़ंक्शन मैक्स शर्तों के उत्पाद में है। यह 3 चर X, Y & Z है। इसलिए, हमें 3 चर K-map की आवश्यकता है। दिए गए अधिकतम शब्द M 0 , M 1 , M 2 और M 4 हैं । ३variable K-map दिए गए अधिकतम शब्दों के अनुरूप शून्य के साथ निम्नलिखित आकृति में दिखाया गया है।

8 आसन्न शून्य या 4 आसन्न शून्य समूह की कोई संभावना नहीं है। 2 निकटवर्ती शून्य को समूहीकृत करने की तीन संभावनाएँ हैं। इन तीन समूहों के बाद, एक भी शून्य नहीं बचा है जैसा कि अनियंत्रित है। 3 variable K-map इन तीनों के साथ groupings निम्नलिखित आकृति में दिखाया गया है।

यहाँ, हमें तीन प्रधान प्रत्यारोपण X + Y, Y + Z & Z + X मिले हैं। ये सभी प्रमुख निहितार्थ हैं essential क्योंकि प्रत्येक समूह में एक शून्य को उनके व्यक्तिगत समूहों के अलावा किसी अन्य समूह द्वारा कवर नहीं किया जाता है।
इसलिए simplified Boolean function है
f = (X + Y).(Y + Z).(Z + X)
इस तरह, हम K-map विधि का उपयोग करके 5 चर तक बूलियन कार्यों को आसानी से सरल कर सकते हैं। 5 से अधिक चर के लिए, के-मैप्स का उपयोग करके कार्यों को सरल करना मुश्किल है। क्योंकि, की संख्याcells K- मानचित्र में मिलता है doubled एक नया चर शामिल करके।
इसके कारण आसन्न लोगों (मिनट की शर्तें) या आसन्न शून्य (अधिकतम पद) की जाँच और समूहन जटिल हो जाएगा। हम चर्चा करेंगेTabular method के-मैप विधि की कठिनाइयों को दूर करने के लिए अगले अध्याय में।
पिछले अध्याय में, हमने के-मैप विधि पर चर्चा की, जो 5 चर तक बूलियन कार्यों को कम करने के लिए एक सुविधाजनक विधि है। लेकिन, इस पद्धति का उपयोग करके 5 से अधिक चर वाले बूलियन कार्यों को सरल करना मुश्किल है।
Quine-McClukey सारणीबद्ध विधि एक प्रमुख विधि है, जो मुख्य निहितार्थ की अवधारणा पर आधारित है। हम जानते हैं किprime implicant एक उत्पाद (या योग) शब्द है, जिसे दिए गए बूलियन फ़ंक्शन के किसी अन्य उत्पाद (या योग) की शर्तों के साथ जोड़कर और कम नहीं किया जा सकता है।
निम्नलिखित बूलियन पहचान का बार-बार उपयोग करके प्रमुख प्रत्यारोपण प्राप्त करने के लिए यह सारणीबद्ध विधि उपयोगी है।
xy + xy '= x (y + y') = x.1 = x
Quine-McCluskey टेबुलर विधि की प्रक्रिया
Quine-McClukey सारणी पद्धति का उपयोग करके बूलियन कार्यों को सरल बनाने के लिए इन चरणों का पालन करें।
Step 1 - दिए गए न्यूनतम शर्तों को व्यवस्थित करें a ascending orderऔर समूहों को उनके बाइनरी अभ्यावेदन में उपस्थित लोगों की संख्या के आधार पर बनाते हैं। तो, वहाँ हो जाएगाat most ‘n+1’ groups अगर बूलियन फ़ंक्शन में 'n' बूलियन वैरिएबल हैं या मिनिमम बाइनरी के बाइनरी समकक्ष में 'n' बिट्स हैं।
Step 2 - में मौजूद न्यूनतम शर्तों की तुलना करें successive groups। यदि केवल एक-बिट स्थिति में परिवर्तन होता है, तो उन दो मिनट की शर्तों को लें। इस प्रतीक को '_' को अलग-अलग स्थिति में रखें और शेष बिट्स को वैसे ही रखें।
Step 3 - जब तक हम सभी नहीं मिलते तब तक नवगठित शब्दों के साथ चरण 2 को दोहराएं prime implicants।
Step 4 - का निरूपण prime implicant table। इसमें पंक्तियों और स्तंभों का समूह होता है। प्राइम इम्प्लांट्स को पंक्ति वार में रखा जा सकता है और न्यूनतम शब्दों को कॉलम वार में रखा जा सकता है। प्रत्येक प्रमुख इम्प्लिकेंट में शामिल की जाने वाली न्यूनतम शर्तों के अनुरूप कोशिकाओं में '1' रखें।
Step 5- प्रत्येक कॉलम का अवलोकन करके आवश्यक प्राइम इम्प्लिकेंट्स का पता लगाएं। यदि मिनिमम टर्म केवल एक प्राइम इम्प्लिकेंट द्वारा कवर किया जाता है, तो यह हैessential prime implicant। उन आवश्यक प्रमुख प्रत्यारोपण सरल बूलियन फ़ंक्शन का हिस्सा होंगे।
Step 6- प्रत्येक आवश्यक प्राइम इम्प्लिकेंट की पंक्तियों को हटाकर और उस आवश्यक प्राइम इम्प्लिकेंट में शामिल की गई शर्तों के अनुसार कॉलम को हटाकर प्राइम इम्पिकेंट टेबल को कम करें। चरण 5 को कम करने के लिए प्रमुख इम्प्लिकेंट टेबल को दोहराएं। जब बूलियन फ़ंक्शन की सभी न्यूनतम शर्तें समाप्त हो जाएँ तो इस प्रक्रिया को रोक दें।
उदाहरण
हमें करने दो simplify निम्नलिखित बूलियन फ़ंक्शन, $f\left ( W,X,Y,Z \right )=\sum m\left ( 2,6,8,9,10,11,14,15 \right )$ Quine-McClukey सारणीबद्ध विधि का उपयोग करना।
दिए गए बूलियन फ़ंक्शन में है sum of min termsप्रपत्र। इसके 4 चर W, X, Y & Z हैं। दिए गए न्यूनतम शब्द 2, 6, 8, 9, 10, 11, 14 और 15 हैं। इन न्यूनतम शर्तों के आरोही क्रम में उनकी मौजूद संख्या के आधार पर बाइनरी समकक्ष 2, 8, 6, 9, 10, 11, 14 और 15. निम्न तालिका इनसे पता चलता हैmin terms and their equivalent binary अभ्यावेदन।
| समूह का नाम | न्यूनतम शर्तें | डब्ल्यू | एक्स | Y | जेड |
|---|---|---|---|---|---|
| GA1 | 2 | 0 | 0 | 1 | 0 |
| 8 | 1 | 0 | 0 | 0 | |
| GA2 | 6 | 0 | 1 | 1 | 0 |
| 9 | 1 | 0 | 0 | 1 | |
| 10 | 1 | 0 | 1 | 0 | |
| 1 1 | 1 | 0 | 1 | 1 | |
| 14 | 1 | 1 | 1 | 0 | |
| GA4 | 15 | 1 | 1 | 1 | 1 |
दी गई न्यूनतम शर्तों को उनके बाइनरी समकक्षों में मौजूद लोगों की संख्या के आधार पर 4 समूहों में व्यवस्थित किया गया है। निम्न तालिका संभव दर्शाती हैmerging of min terms आसन्न समूहों से।
| समूह का नाम | न्यूनतम शर्तें | डब्ल्यू | एक्स | Y | जेड |
|---|---|---|---|---|---|
| GB1 | 2,6 | 0 | - | 1 | 0 |
| 2,10 | - | 0 | 1 | 0 | |
| 8,9 | 1 | 0 | 0 | - | |
| 8,10 | 1 | 0 | - | 0 | |
| GB2 | 6,14 | - | 1 | 1 | 0 |
| 9,11 | 1 | 0 | - | 1 | |
| 10,11 | 1 | 0 | 1 | - | |
| 10,14 | 1 | - | 1 | 0 | |
| 11,15 | 1 | - | 1 | 1 | |
| 14,15 | 1 | 1 | 1 | - |
न्यूनतम शब्द, जो आसन्न समूहों से केवल एक-बिट स्थिति में भिन्न होते हैं, को मिला दिया जाता है। उस भिन्न बिट को इस प्रतीक के साथ दर्शाया गया है, '-'। इस मामले में, तीन समूह हैं और प्रत्येक समूह में दो मिनट की शर्तें हैं। निम्न तालिका संभव दर्शाती हैmerging of min term pairs आसन्न समूहों से।
| समूह का नाम | न्यूनतम शर्तें | डब्ल्यू | एक्स | Y | जेड |
|---|---|---|---|---|---|
| GB1 | 2,6,10,14 | - | - | 1 | 0 |
| 2,10,6,14 | - | - | 1 | 0 | |
| 8,9,10,11 | 1 | 0 | - | - | |
| 8,10,9,11 | 1 | 0 | - | - | |
| GB2 | 10,11,14,15 | 1 | - | 1 | - |
| 10,14,11,15 | 1 | - | 1 | - |
न्यूनतम टर्म जोड़े के क्रमिक समूह, जो केवल एक-बिट स्थिति में भिन्न होते हैं, विलय किए जाते हैं। उस भिन्न बिट को इस प्रतीक के साथ दर्शाया गया है, '-'। इस मामले में, दो समूह हैं और प्रत्येक समूह में चार मिनट की शर्तों के संयोजन हैं। यहां, 4 मिनट की शर्तों के ये संयोजन दो पंक्तियों में उपलब्ध हैं। तो, हम दोहराया पंक्तियों को हटा सकते हैं। निरर्थक पंक्तियों को हटाने के बाद कम तालिका नीचे दिखाई गई है।
| समूह का नाम | न्यूनतम शर्तें | डब्ल्यू | एक्स | Y | जेड |
|---|---|---|---|---|---|
| GC1 | 2,6,10,14 | - | - | 1 | 0 |
| 8,9,10,11 | 1 | 0 | - | - | |
| GC2 | 10,11,14,15 | 1 | - | 1 | - |
निकटवर्ती समूहों से न्यूनतम शर्तों के संयोजन का आगे विलय संभव नहीं है, क्योंकि वे एक से अधिक बिट स्थिति में भिन्न होते हैं। उपरोक्त तालिका में तीन पंक्तियाँ हैं। तो, प्रत्येक पंक्ति एक प्रमुख निहितार्थ देगी। इसलिएprime implicants YZ ', WX' और WY हैं।
prime implicant table नीचे दिखाया गया है।
| न्यूनतम शर्तें / प्रधान प्रत्यारोपण | 2 | 6 | 8 | 9 | 10 | 1 1 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|
| YZ’ | 1 | 1 | 1 | 1 | ||||
| WX’ | 1 | 1 | 1 | 1 | ||||
| WY | 1 | 1 | 1 | 1 |
प्राइम इम्प्लांट्स को पंक्तिवार रखा जाता है और न्यूनतम शब्दों को कॉलम वार में रखा जाता है। 1s को प्राइम इम्पिकेंट रो के कॉमन सेल्स और संबंधित मिनिमम टर्म कॉलम में रखा जाता है।
2 और 6 मिनट की शर्तें केवल एक प्रमुख इम्प्लिकेंट द्वारा कवर की जाती हैं YZ’। तो, यह एक हैessential prime implicant। यह सरलीकृत बूलियन फ़ंक्शन का हिस्सा होगा। अब, इस प्राइम इम्प्लिकेंट पंक्ति और संबंधित मिनिमम कॉलम को हटा दें। घटी हुई प्राइम इम्प्रिकेंट टेबल नीचे दी गई है।
| न्यूनतम शर्तें / प्रधान प्रत्यारोपण | 8 | 9 | 1 1 | 15 |
|---|---|---|---|---|
| WX’ | 1 | 1 | 1 | |
| WY | 1 | 1 |
8 और 9 मिनट की शर्तें केवल एक प्रमुख इम्प्लिकेंट द्वारा कवर की जाती हैं WX’। तो, यह एक हैessential prime implicant। यह सरलीकृत बूलियन फ़ंक्शन का हिस्सा होगा। अब, इस प्राइम इम्प्लिकेंट पंक्ति और संबंधित मिनिमम कॉलम को हटा दें। घटी हुई प्राइम इम्प्रिकेंट टेबल नीचे दी गई है।
| न्यूनतम शर्तें / प्रधान प्रत्यारोपण | 15 |
|---|---|
| WY | 1 |
15 शब्द की अवधि केवल एक प्रमुख निहितार्थ द्वारा कवर की जाती है WY। तो, यह एक हैessential prime implicant। यह सरलीकृत बूलियन फ़ंक्शन का हिस्सा होगा।
इस उदाहरण की समस्या में, हमें तीन प्रधान प्रभावक मिले और तीनों आवश्यक हैं। इसलिएsimplified Boolean function है
f(W,X,Y,Z) = YZ’ + WX’ + WY.
डिजिटल इलेक्ट्रॉनिक सर्किट वोल्टेज के साथ काम करते हैं two logic levelsजिसका नाम लॉजिक लो और लॉजिक हाई है। लॉजिक लो के अनुरूप वोल्टेज की श्रेणी को '0' के साथ दर्शाया गया है। इसी तरह, तर्क उच्च के अनुरूप वोल्टेज की श्रेणी को '1' के साथ दर्शाया गया है।
बुनियादी डिजिटल इलेक्ट्रॉनिक सर्किट जिसमें एक या अधिक इनपुट होते हैं और एकल आउटपुट होता है Logic gate। इसलिए, तर्क द्वार किसी भी डिजिटल सिस्टम के निर्माण खंड हैं। हम इन लॉजिक गेट्स को निम्नलिखित तीन श्रेणियों में वर्गीकृत कर सकते हैं।
- मूल द्वार
- यूनिवर्सल गेट्स
- विशेष द्वार
अब, तर्क गेट्स के बारे में चर्चा करते हैं जो प्रत्येक श्रेणी में एक-एक करके आते हैं।
बेसिक गेट्स
पहले के अध्यायों में, हमने सीखा कि बूलियन कार्यों को उत्पादों के योग में या आवश्यकता के आधार पर रकम के रूप में प्रस्तुत किया जा सकता है। इसलिए, हम बुनियादी फाटकों का उपयोग करके इन बूलियन कार्यों को लागू कर सकते हैं। मूल द्वार AND, OR NOT NOT द्वार हैं।
और गेट
एक और गेट एक डिजिटल सर्किट है जिसमें दो या दो से अधिक इनपुट होते हैं और आउटपुट उत्पन्न करते हैं, जो कि है logical ANDउन सभी इनपुट्स की। यह प्रतिनिधित्व करने के लिए वैकल्पिक हैLogical AND प्रतीक के साथ '।'
निम्न तालिका से पता चलता है truth table 2-इनपुट और गेट के।
| ए | ख | य = एबी |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
यहाँ A, B इनपुट हैं और Y दो इनपुट और गेट का आउटपुट है। यदि दोनों इनपुट '1' हैं, तो केवल आउटपुट, Y '1' है। इनपुट्स के शेष संयोजनों के लिए, आउटपुट 'Y' है।
निम्नलिखित आंकड़ा दिखाता है symbol एक और गेट, जिसमें दो इनपुट ए, बी और एक आउटपुट है, वाई।

यह और गेट एक आउटपुट (Y) का उत्पादन करता है, जो कि है logical ANDदो इनपुट ए, बी। इसी तरह, यदि 'एन' इनपुट हैं, तो एंड गेट एक आउटपुट का उत्पादन करता है, जो उन सभी इनपुटों का तार्किक AND है। इसका मतलब है कि, AND गेट का आउटपुट '1' होगा, जब सभी इनपुट '1' होंगे।
या गेट
OR OR गेट एक डिजिटल सर्किट है जिसमें दो या दो से अधिक इनपुट होते हैं और आउटपुट उत्पन्न करते हैं, जो उन सभी इनपुटों का तार्किक OR है। यहlogical OR प्रतीक '+' के साथ दर्शाया गया है।
निम्न तालिका से पता चलता है truth table 2-इनपुट या गेट के।
| ए | ख | य = अ + ब |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
यहाँ A, B इनपुट हैं और Y दो इनपुट या गेट का आउटपुट है। यदि दोनों इनपुट '0' हैं, तो केवल आउटपुट, Y '0' है। इनपुट्स के शेष संयोजनों के लिए, आउटपुट 'Y' है।
निम्नलिखित आंकड़ा दिखाता है symbol OR गेट के, जिसमें दो इनपुट A, B और एक आउटपुट है, Y।

यह या गेट एक आउटपुट (Y) का उत्पादन करता है, जो कि है logical ORदो इनपुट ए, बी। इसी तरह, अगर 'एन' इनपुट हैं, तो ओआर गेट एक आउटपुट का उत्पादन करता है, जो उन सभी इनपुटों का तार्किक OR है। इसका मतलब है कि, OR गेट का आउटपुट '1' होगा, जब कम से कम एक इनपुट '1' होगा।
गेट नहीं
नॉट गेट एक डिजिटल सर्किट है जिसमें सिंगल इनपुट और सिंगल आउटपुट होता है। गेट का आउटपुट नहीं हैlogical inversionइनपुट के इसलिए, NOT गेट को इन्वर्टर भी कहा जाता है।
निम्न तालिका से पता चलता है truth table गेट का नहीं।
| ए | Y = A ' |
|---|---|
| 0 | 1 |
| 1 | 0 |
यहाँ A और Y क्रमशः गेट के इनपुट और आउटपुट नहीं हैं। यदि इनपुट, A '0' है, तो आउटपुट, Y '1' है। इसी तरह, यदि इनपुट, ए '1' है, तो आउटपुट, वाई '0' है।
निम्नलिखित आंकड़ा दिखाता है symbol गेट का नहीं, जिसमें एक इनपुट, ए और एक आउटपुट है, वाई।

यह गेट एक आउटपुट (Y) का उत्पादन नहीं करता है, जो कि है complement इनपुट के, ए।
यूनिवर्सल गेट्स
NAND & NOR गेट्स को कहा जाता है universal gates। क्योंकि हम किसी भी बूलियन फ़ंक्शन को लागू कर सकते हैं, जो अकेले NAND गेट्स का उपयोग करके उत्पादों के रूप में है। इसी तरह, हम किसी भी बूलियन फ़ंक्शन को लागू कर सकते हैं, जो अकेले NOR गेट्स का उपयोग करके रकम के उत्पाद में है।
नंद द्वार
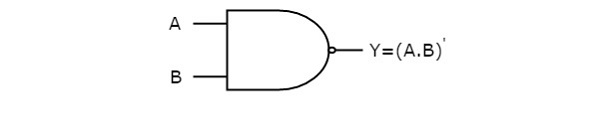
एनएएनडी गेट एक डिजिटल सर्किट है जिसमें दो या दो से अधिक इनपुट होते हैं और एक आउटपुट उत्पन्न करता है, जो है inversion of logical AND उन सभी इनपुट्स की।
निम्न तालिका से पता चलता है truth table 2-इनपुट नंद द्वार का।
| ए | ख | Y = (एबी) ' |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
यहाँ A, B इनपुट हैं और Y दो इनपुट NAND गेट का आउटपुट है। जब दोनों इनपुट '1' हैं, तो आउटपुट 'Y' है। यदि कम से कम एक इनपुट शून्य है, तो आउटपुट, Y '1' है। यह दो इनपुट और गेट ऑपरेशन के ठीक विपरीत है।
निम्न छवि दिखाती है symbol नंद द्वार, जिसमें दो इनपुट ए, बी और एक आउटपुट है, वाई।
एनएएनडी गेट का संचालन उसी प्रकार से होता है जैसे गेट और इनवर्टर के बाद होता है। इसीलिए NAND गेट सिंबल को ऐसे ही दर्शाया जाता है।
NOR गेट
NOR गेट एक डिजिटल सर्किट है जिसमें दो या दो से अधिक इनपुट होते हैं और एक आउटपुट उत्पन्न करता है, जो कि है inversion of logical OR उन सभी इनपुट्स की।
निम्न तालिका से पता चलता है truth table 2-इनपुट NOR गेट के
| ए | ख | Y = (ए + बी) ' |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
यहाँ A, B इनपुट हैं और Y आउटपुट है। यदि दोनों इनपुट '0' हैं, तो आउटपुट, Y '1' है। यदि इनपुट में से कम से कम एक '1' है, तो आउटपुट, Y '0' है। यह दो इनपुट या गेट ऑपरेशन के ठीक विपरीत है।
निम्नलिखित आंकड़ा दिखाता है symbol NOR गेट के, जिसमें दो इनपुट A, B और एक आउटपुट है, Y।

एनओआर गेट ऑपरेशन ओआर गेट की तरह ही होता है और इसके बाद इनवर्टर होता है। यही कारण है कि NOR गेट प्रतीक को इस तरह से दर्शाया गया है।
विशेष द्वार
Ex-OR & Ex-NOR गेट्स को विशेष गेट्स कहा जाता है। क्योंकि, ये दो द्वार OR & NOR द्वार के विशेष मामले हैं।
पूर्व या गेट
Ex-OR फाटक का पूर्ण रूप है Exclusive-ORद्वार। इसका कार्य कुछ मामलों को छोड़कर OR गेट के समान है, जब इनपुट में सम संख्या वाले होते हैं।
निम्न तालिका से पता चलता है truth table 2-इनपुट पूर्व या गेट।
| ए | ख | य = अ⊕ब |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
यहाँ A, B इनपुट हैं और Y दो इनपुट Ex-OR गेट का आउटपुट है। Ex-OR गेट की सत्य तालिका पहले तीन पंक्तियों के लिए OR गेट के समान है। एकमात्र संशोधन चौथी पंक्ति में है। इसका मतलब है कि, आउटपुट इनपुट (Y) एक के बजाय शून्य है, जब दोनों इनपुट एक होते हैं, क्योंकि इनपुट्स की संख्या भी होती है।
इसलिए, Ex-OR गेट का आउटपुट '1' है, जब दोनों में से केवल एक इनपुट '1' है। और यह शून्य है, जब दोनों इनपुट समान हैं।
नीचे आंकड़ा दिखाता है symbol एक्स-ओआर गेट, जिसमें दो इनपुट ए, बी और एक आउटपुट है, वाई।

Ex-OR गेट ऑपरेशन, OR गेट के समान है, इनपुट के कुछ संयोजन (ओं) को छोड़कर। इसीलिए Ex-OR गेट सिंबल को ऐसे ही दर्शाया जाता है। Ex-OR गेट का आउटपुट '1' है, जब इनपुट पर मौजूद विषम संख्या। इसलिए, Ex-OR गेट के आउटपुट को भी कहा जाता हैodd function।
पूर्व NOR गेट
Ex-NOR फाटक का पूर्ण रूप है Exclusive-NORद्वार। इसका कार्य कुछ मामलों को छोड़कर NOR फाटक के समान है, जब आदानों की संख्या अधिक होती है।
निम्न तालिका से पता चलता है truth table 2-इनपुट पूर्व NOR गेट।
| ए | ख | य = अ⊙ब |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
यहाँ A, B इनपुट हैं और Y आउटपुट है। Ex-NOR गेट की सत्य तालिका पहली तीन पंक्तियों के लिए NOR गेट की तरह ही है। एकमात्र संशोधन चौथी पंक्ति में है। इसका मतलब है, आउटपुट शून्य के बजाय एक है, जब दोनों इनपुट एक हैं।
इसलिए, Ex-NOR गेट का आउटपुट '1' है, जब दोनों इनपुट समान हैं। और यह शून्य है, जब दोनों इनपुट अलग-अलग हैं।
निम्नलिखित आंकड़ा दिखाता है symbol एक्स-एनआर गेट, जिसमें दो इनपुट ए, बी और एक आउटपुट है, वाई।

एक्स-एनआर गेट ऑपरेशन, नॉर्म गेट के समान है, इनपुट के कुछ संयोजन (ओं) को छोड़कर। इसीलिए Ex-NOR गेट सिंबल को ऐसे ही दर्शाया जाता है। एक्स-एनओआर गेट का आउटपुट '1' है, जब इनपुट पर मौजूद लोगों की संख्या भी। इसलिए, Ex-NOR गेट के आउटपुट को भी कहा जाता हैeven function।
Ex-OR & Ex-NOR लॉजिक गेट्स के उपरोक्त सत्य तालिकाओं से, हम आसानी से नोटिस कर सकते हैं कि Ex-NOR ऑपरेशन Ex-OR ऑपरेशन का तार्किक उलटा है।
इनपुट और आउटपुट के बीच मौजूद स्तरों की अधिकतम संख्या दो में है two level logic। इसका मतलब है, तर्क गेट्स की कुल संख्या के बावजूद, किसी भी इनपुट और आउटपुट के बीच मौजूद लॉजिक गेट्स की अधिकतम संख्या दो स्तर के लॉजिक में दो है। यहाँ, प्रथम स्तर तर्क गेट्स के आउटपुट दूसरे स्तर तर्क गेट (एस) के इनपुट के रूप में जुड़े हुए हैं।
चार तर्क द्वार और, या, नंद और NOR पर विचार करें। चूंकि, 4 तर्क द्वार हैं, इसलिए हमें दो स्तरीय तर्क को साकार करने के 16 संभावित तरीके मिलेंगे। ये हैं AND-AND, AND-OR, ANDNAND, AND-NOR, OR-AND, OR-NAND, OR-NOR, NAND-AND, NAND-OR, NANDNAND, NAND-NOR, NOR-AND और NOR-OR, NOR-NAND, NOR-NOR।
इन दो स्तरीय तर्क बोधों को निम्नलिखित दो श्रेणियों में वर्गीकृत किया जा सकता है।
- अपक्षयी रूप
- गैर-अपक्षयी रूप
अपक्षयी रूप
यदि एकल तर्क गेट का उपयोग करके दो स्तर के तर्क बोध का उत्पादन प्राप्त किया जा सकता है, तो इसे कहा जाता है degenerative form। जाहिर है, सिंगल लॉजिक गेट के इनपुट की संख्या बढ़ती है। इसके कारण लॉजिक गेट की फैन-इन बढ़ जाती है। यह अपक्षयी रूप का एक लाभ है।
केवल 6 combinations16 संयोजनों में से दो स्तर के तर्क बोध को पतनशील रूप में आते हैं। वो हैं AND-AND, AND-NAND, OR-OR, OR-NOR, NAND-NOR, NORNAND।
इस भाग में, आइए कुछ वास्तविकताओं पर चर्चा करें। मान लें, A, B, C & D इनपुट हैं और Y प्रत्येक तर्क बोध में आउटपुट है।
और-तर्क
इस तर्क बोध में, और द्वार दोनों स्तरों में मौजूद हैं। नीचे दिया गया आंकड़ा इसके लिए एक उदाहरण दिखाता हैAND-AND logic प्राप्ति।

हम पहले स्तर के तर्क गेट्स के आउटपुट प्राप्त करेंगे $Y_{1}=AB$ तथा $Y_{2}=CD$
ये आउटपुट, $Y_{1}$ तथा $Y_{2}$दूसरे स्तर में मौजूद AND गेट के इनपुट के रूप में लागू होते हैं। तो, इस और गेट का आउटपुट है
$$Y=Y_{1}Y_{2}$$
विकल्प $Y_{1}$ तथा $Y_{2}$ उपरोक्त समीकरण में मूल्य।
$$Y=\left ( AB \right )\left ( CD \right )$$
$\Rightarrow Y=ABCD$
इसलिए, इस AND-AND तर्क बोध का आउटपुट है ABCD। यह बूलियन फ़ंक्शन 4 इनपुट और गेट का उपयोग करके कार्यान्वित किया जा सकता है। इसलिए, यह हैdegenerative form।
और नंद तर्क
इस तर्क बोध में, और द्वार पहले स्तर में मौजूद हैं और NAND गेट (s) दूसरे स्तर में मौजूद हैं। निम्नलिखित आंकड़ा के लिए एक उदाहरण दिखाता हैAND-NAND logic प्राप्ति।
पहले, हमें पहले स्तर के लॉजिक गेट्स के आउटपुट मिलते थे $Y_{1} = AB$ तथा $Y_{2} = CD$
ये आउटपुट,$Y_{1}$ तथा $Y_{2}$NAND गेट के इनपुट के रूप में लागू किया जाता है जो दूसरे स्तर पर मौजूद होता है। तो, इस NAND गेट का आउटपुट है
$$Y={\left ( Y_{1}Y_{2} \right )}'$$
विकल्प $Y_{1}$ तथा $Y_{2}$ उपरोक्त समीकरण में मूल्य।
$$Y={\left ( \left ( AB \right ) \left ( CD \right )\right )}'$$
$\Rightarrow Y={\left ( ABCD \right )}'$
इसलिए, इस और नंद तर्क बोध का उत्पादन है ${\left ( ABCD \right )}'$। यह बूलियन फ़ंक्शन 4 इनपुट एनएएनडी गेट का उपयोग करके कार्यान्वित किया जा सकता है। इसलिए, यह हैdegenerative form।
OR- या तर्क
इस तर्क बोध में, या द्वार दोनों स्तरों में मौजूद हैं। निम्नलिखित आंकड़ा के लिए एक उदाहरण दिखाता हैOR-OR logic प्राप्ति।
हम पहले स्तर के तर्क गेट्स के आउटपुट प्राप्त करेंगे $Y_{1}=A+B$ तथा $Y_{2}=C+D$।
ये आउटपुट, $Y_{1}$ तथा $Y_{2}$दूसरे स्तर में मौजूद OR गेट के इनपुट के रूप में लागू किया जाता है। तो, इस OR गेट का आउटपुट है
$$Y=Y_{1}+Y_{2}$$
विकल्प $Y_{1}$ तथा $Y_{2}$ उपरोक्त समीकरण में मूल्य।
$$Y=\left ( A+B \right )+\left ( C+D \right )$$
$\Rightarrow Y=A+B+C+D$
इसलिए, इस OR-OR तर्क बोध का आउटपुट है A+B+C+D। यह बूलियन फ़ंक्शन 4 इनपुट या गेट का उपयोग करके कार्यान्वित किया जा सकता है। इसलिए, यह हैdegenerative form।
इसी तरह, आप सत्यापित कर सकते हैं कि शेष बचे हुए हिस्से इस श्रेणी के हैं या नहीं।
गैर-अपक्षयी रूप
यदि एकल तर्क गेट का उपयोग करके दो स्तरीय तर्क प्राप्ति का आउटपुट प्राप्त नहीं किया जा सकता है, तो इसे कहा जाता है non-degenerative form।
बचा हुआ 10 combinationsदो स्तर के तर्क का अहसास नोंडेगेंनेरेटिव फॉर्म के अंतर्गत आता है। ये हैं AND-OR, AND-NOR, OR-AND, OR-NAND, NAND-AND, NANDOR, NAND-NAND, NOR-AND, NOR-OR, NOR-NOR।
अब, कुछ वास्तविकताओं पर चर्चा करते हैं। मान लें, A, B, C & D इनपुट हैं और Y प्रत्येक तर्क बोध में आउटपुट है।
और-या तर्क
इस तर्क बोध में, और द्वार पहले स्तर में मौजूद हैं और दूसरे स्तर में OR गेट (s) मौजूद हैं। नीचे दिया गया आंकड़ा इसके लिए एक उदाहरण दिखाता हैAND-OR logic प्राप्ति।

पहले, हमें पहले स्तर के लॉजिक गेट्स के आउटपुट मिलते थे $Y_{1} = AB$ तथा $Y_{2} = CD$।
ये आउटपुट, Y1 और Y2 को OR गेट के इनपुट के रूप में लागू किया जाता है जो दूसरे स्तर पर मौजूद होता है। तो, इस OR गेट का आउटपुट है
$$Y=Y_{1}+Y_{2}$$
विकल्प $Y_{1}$ तथा $Y_{2}$ उपरोक्त समीकरण में मूल्य
$$Y=AB+CD$$
इसलिए, इस AND-OR तर्क बोध का आउटपुट है AB+CD। यह बूलियन फ़ंक्शन में हैSum of Productsप्रपत्र। चूंकि, हम सिंगल लॉजिक गेट का उपयोग करके इसे लागू नहीं कर सकते हैं, यह AND-OR लॉजिक अहसास हैnon-degenerative form।
और- NOR तर्क
इस तर्क बोध में, और द्वार प्रथम स्तर में मौजूद हैं और NOR गेट (s) दूसरे स्तर में मौजूद हैं। निम्नलिखित आंकड़ा के लिए एक उदाहरण दिखाता हैAND-NOR logic प्राप्ति।

हम पहले स्तर के तर्क गेट्स के आउटपुट को जानते हैं $Y_{1} = AB$ तथा $Y_{2} = CD$
ये आउटपुट, Y1 और Y2 को NOR गेट के इनपुट के रूप में लागू किया जाता है जो दूसरे स्तर पर मौजूद होता है। तो, इस NOR गेट का आउटपुट है
$$Y={\left ( Y_{1}+Y_{2} \right )}'$$
विकल्प $Y_{1}$ तथा $Y_{2}$ उपरोक्त समीकरण में मूल्य।
$$Y={\left ( AB+CD \right )}'$$
इसलिए, इस AND-NOR तर्क प्राप्ति का आउटपुट है ${\left ( AB+CD \right )}'$। यह बूलियन फ़ंक्शन में हैAND-OR-Invertप्रपत्र। चूंकि, हम सिंगल लॉजिक गेट का उपयोग करके इसे लागू नहीं कर सकते हैं, यह AND-NOR लॉजिक अहसास हैnon-degenerative form
OR- और तर्क
इस तर्क बोध में, या गेट पहले स्तर में मौजूद हैं और दूसरे स्तर में गेट (एस) मौजूद हैं। निम्नलिखित आंकड़ा के लिए एक उदाहरण दिखाता हैOR-AND logic प्राप्ति।

पहले, हमें पहले स्तर के लॉजिक गेट्स के आउटपुट मिलते थे $Y_{1}=A+B$ तथा $Y_{2}=C+D$।
ये आउटपुट, $Y_{1}$ तथा $Y_{2}$दूसरे स्तर में मौजूद AND गेट के इनपुट के रूप में लागू होते हैं। तो, इस और गेट का आउटपुट है
$$Y=Y_{1}Y_{2}$$
विकल्प $Y_{1}$ तथा $Y_{2}$ उपरोक्त समीकरण में मूल्य।
$$Y = \left ( A+B \right )\left ( C+D \right )$$
इसलिए, इस OR-AND तर्क बोध का आउटपुट है (A + B) (C + D)। यह बूलियन फ़ंक्शन में हैProduct of Sumsप्रपत्र। चूंकि, हम सिंगल लॉजिक गेट का उपयोग करके इसे लागू नहीं कर सकते, यह OR-AND और लॉजिक अहसास हैnon-degenerative form।
इसी तरह, आप सत्यापित कर सकते हैं कि शेष बचे हुए हिस्से इस श्रेणी के हैं या नहीं।
Combinational circuitsतर्क द्वार से मिलकर। ये सर्किट बाइनरी मान के साथ संचालित होते हैं। कॉम्बिनेशन सर्किट का आउटपुट (एस) वर्तमान इनपुट के संयोजन पर निर्भर करता है। निम्नलिखित आंकड़ा दिखाता हैblock diagram कॉम्बिनेशन सर्किट का।

इस कॉम्बिनेशन सर्किट में 'n' इनपुट वैरिएबल और 'm' आउटपुट हैं। इनपुट चर का प्रत्येक संयोजन आउटपुट (ओं) को प्रभावित करेगा।
संयोजन सर्किट की डिजाइन प्रक्रिया
दिए गए विनिर्देशों से इनपुट चर और आउटपुट की आवश्यक संख्या का पता लगाएं।
का निरूपण करें Truth table। यदि 'एन' इनपुट चर हैं, तो 2n संभव संयोजन होंगे। इनपुट के प्रत्येक संयोजन के लिए, आउटपुट मान ढूंढें।
खोजो Boolean expressionsप्रत्येक आउटपुट के लिए। यदि आवश्यक हो, तो उन अभिव्यक्तियों को सरल बनाएं।
उपरोक्त बूलियन अभिव्यक्ति का उपयोग करके प्रत्येक आउटपुट के अनुरूप लागू करें Logic gates।
कोड कन्वर्टर्स
हमने कोड नाम के अध्याय में विभिन्न कोडों पर चर्चा की है। कन्वर्टर्स, जो एक कोड को दूसरे कोड में बदलते हैं, उन्हें कहा जाता हैcode converters। ये कोड कन्वर्टर्स मूल रूप से लॉजिक गेट से मिलकर बने होते हैं।
उदाहरण
ग्रे कोड कनवर्टर करने के लिए बाइनरी कोड
आइए हम एक कनवर्टर लागू करते हैं, जो 4-बिट बाइनरी कोड WXYZ को उसके समकक्ष ग्रे कोड ABCD में परिवर्तित करता है।
निम्न तालिका से पता चलता है Truth table ग्रे कोड कनवर्टर करने के लिए एक 4-बिट बाइनरी कोड का।
| बाइनरी कोड WXYZ | WXYZ ग्रे कोड ABCD |
|---|---|
| 0000 | 0000 |
| 0001 | 0001 |
| 0010 | 0011 |
| 0011 | 0010 |
| 0100 | 0110 |
| 0101 | 0111 |
| 0110 | 0101 |
| 0111 | 0100 |
| 1000 | 1100 |
| 1001 | 1101 |
| 1010 | 1111 |
| 1011 | 1110 |
| 1100 | 1010 |
| 1101 | 1011 |
| 1110 | 1001 |
| 1111 | 1000 |
ट्रुथ टेबल से, हम लिख सकते हैं Boolean functions नीचे के रूप में ग्रे कोड के प्रत्येक आउटपुट बिट के लिए।
$$A=\sum m\left (8,9,10,11,12,13,14,15 \right )$$
$$B=\sum m\left (4,5,6,7,8,9,10,11 \right )$$
$$C=\sum m\left (2,3,4,5,10,11,12,13 \right )$$
$$D=\sum m\left (1,2,5,6,9,10,13,14 \right )$$
4 चर K-Maps का उपयोग करके उपरोक्त कार्यों को सरल बनाते हैं।
निम्नलिखित आंकड़ा दिखाता है 4 variable K-Map सरलीकरण के लिए Boolean function, A।

8 आसन्न लोगों को समूहीकृत करके $A=W$।
निम्नलिखित आंकड़ा दिखाता है 4 variable K-Map सरलीकरण के लिए Boolean function, B।

4 आसन्न लोगों के दो समूह हैं। समूहीकरण के बाद, हम बी को प्राप्त करेंगे
$$B={W}'X+W{X}'=W\oplus X $$
इसी तरह, हम सरलीकरण के बाद C & D के लिए निम्नलिखित बूलियन फ़ंक्शन प्राप्त करेंगे।
$$C={X}'Y+X{Y}'=X \oplus Y$$
$$D={Y}'Z+Y{Z}'=Y \oplus Z$$
निम्नलिखित आंकड़ा दिखाता है circuit diagram ग्रे कोड कनवर्टर करने के लिए 4-बिट बाइनरी कोड।

चूंकि आउटपुट केवल वर्तमान इनपुट पर निर्भर करते हैं, इसलिए ग्रे कोड कनवर्टर के लिए यह 4-बिट बाइनरी कोड एक संयोजन सर्किट है। इसी तरह, आप अन्य कोड कन्वर्टर्स को लागू कर सकते हैं।
पैरिटी बिट जेनरेटर
समता बिट के प्रकार के आधार पर दो प्रकार के समता बिट जनरेटर उत्पन्न होते हैं। Even parity generatorसम समरूपता उत्पन्न करता है। इसी तरह,odd parity generator एक अजीब समता बिट उत्पन्न करता है।
यहां तक कि पैरिटी जेनरेटर भी
अब, हमें एक 3-बिट बाइनरी इनपुट, WXY के लिए समरूप जनरेटर लागू करते हैं। यह सम समता बिट उत्पन्न करता है, पी। यदि इनपुट में मौजूद विषम संख्याएँ हैं, तो समता बिट भी, P को '1' होना चाहिए ताकि परिणामी शब्द में सम संख्या हो। इनपुट के अन्य संयोजनों के लिए, समता बिट, P को '0' होना चाहिए। निम्न तालिका से पता चलता हैTruth table समता जनक का भी।
| बाइनरी इनपुट WXY | यहां तक कि पैरिटी बिट पी |
|---|---|
| 000 | 0 |
| 001 | 1 |
| 010 | 1 |
| 011 | 0 |
| 100 | 1 |
| 101 | 0 |
| 110 | 0 |
| 111 | 1 |
उपरोक्त सत्य तालिका से, हम लिख सकते हैं Boolean function समता बिट के लिए भी
$$P={W}'{X}'Y+{W}'X{Y}'+W{X}'{Y}'+WXY$$
$\Rightarrow P={W}'\left ( {X}'Y+X{Y}' \right )+W\left ({X}'{Y}'+XY \right )$
$\Rightarrow P={W}'\left ( X \oplus Y \right )+W{\left (X \oplus Y \right )}'=W \oplus X \oplus Y$
निम्नलिखित आंकड़ा दिखाता है circuit diagram समता जनक का भी।

इस सर्किट में दो होते हैं Exclusive-OR gatesदो इनपुट प्रत्येक होने। पहला एक्सक्लूसिव गेट जिसमें दो इनपुट W & X हैं और एक आउटपुट W This X का उत्पादन करता है। इस आउटपुट को दूसरे एक्सक्लूसिव-ओर गेट के एक इनपुट के रूप में दिया जाता है। इस दूसरे विशेष-OR गेट का दूसरा इनपुट Y है और W ⊕ X। Y का आउटपुट उत्पन्न करता है।
विषम समता जनक
यदि इनपुट में मौजूद लोगों की संख्या, तो विषम समता बिट, P '1' होना चाहिए, ताकि परिणामी शब्द में विषम संख्याएं हों। इनपुट के अन्य संयोजनों के लिए, विषम समता बिट, P '0' होना चाहिए।
विषम समता जनरेटर को लागू करने के लिए समता जनरेटर की समान प्रक्रिया का पालन करें। circuit diagram विषम समता जनरेटर निम्नलिखित आकृति में दिखाया गया है।

उपरोक्त सर्किट आरेख में पहले स्तर में Ex-OR गेट और दूसरे स्तर में Ex-NOR गेट हैं। चूँकि विषम समता समता के ठीक विपरीत है, हम समता जनक के आउटपुट में एक इन्वर्टर लगा सकते हैं। उस स्थिति में, पहले और दूसरे स्तर में प्रत्येक स्तर में एक EXOR गेट होता है और तीसरे स्तर में एक इन्वर्टर होता है।
पैरिटी चेकर
समता के प्रकार के आधार पर दो प्रकार के समता चेकर्स की जाँच की जानी है। Even parity checkerप्रेषित डेटा में त्रुटि की जाँच करता है, जिसमें समता के साथ संदेश बिट्स भी होते हैं। इसी तरह,odd parity checker प्रेषित डेटा में त्रुटि की जाँच करता है, जिसमें विषम समता के साथ संदेश बिट्स होते हैं।
समता चेकर
अब, एक समता चेकर सर्किट को लागू करते हैं। मान लें कि एक 3-बिट बाइनरी इनपुट है, WXY को सम समरूप बिट के साथ प्रेषित किया जाता है। इसलिए, परिणामी शब्द (डेटा) में 4 बिट्स होते हैं, जो सम समता परीक्षक के इनपुट के रूप में प्राप्त किया जाएगा।
यह एक उत्पन्न करता है even parity check bit, E। यह बिट शून्य होगा, यदि प्राप्त डेटा में सम संख्या वाले होते हैं। इसका मतलब है, प्राप्त आंकड़ों में कोई त्रुटि नहीं है। यह समता चेक बिट एक होगा, यदि प्राप्त आंकड़ों में विषम संख्या है। इसका मतलब है, प्राप्त डेटा में कोई त्रुटि है।
निम्न तालिका से पता चलता है Truth table एक समता परीक्षक की।
| 4-बिट प्राप्त डेटा WXYP | यहां तक कि समता चेक बिट ई |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 1 |
| 0011 | 0 |
| 0100 | 1 |
| 0101 | 0 |
| 0110 | 0 |
| 0111 | 1 |
| 1000 | 1 |
| 1001 | 0 |
| 1010 | 0 |
| 1011 | 1 |
| 1100 | 0 |
| 1101 | 1 |
| 1110 | 1 |
| 1111 | 0 |
उपरोक्त सत्य तालिका से, हम देख सकते हैं कि समता चेक बिट मान '1' है, जब प्राप्त आंकड़ों में मौजूद विषम संख्या। इसका मतलब है कि समता चेक बिट का बूलियन फ़ंक्शन एक हैodd function। विशेष-या फ़ंक्शन इस स्थिति को संतुष्ट करता है। इसलिए, हम सीधे लिख सकते हैंBoolean function समता की जाँच बिट के रूप में
$$E=W \oplus X \oplus Y \oplus P$$
निम्नलिखित आंकड़ा दिखाता है circuit diagram समता चेकर का भी।

इस सर्किट में तीन होते हैं Exclusive-OR gatesदो इनपुट प्रत्येक होने। पहले स्तर के गेट्स के आउटपुट उत्पन्न करते हैं$W \oplus X$ और $Y \oplus P$। एक्सक्लूसिव-ओआर गेट, जो दूसरे स्तर पर है, का उत्पादन करता है$W \oplus X \oplus Y \oplus P$
अजीब समानता परीक्षक
एक 3-बिट बाइनरी इनपुट मान लें, WXY को विषम समता बिट के साथ प्रेषित किया जाता है, इसलिए, परिणामी शब्द (डेटा) में 4 बिट्स होते हैं, जो विषम समता चेकर के इनपुट के रूप में प्राप्त होगा।
यह एक उत्पन्न करता है odd parity check bit, E। यह बिट शून्य होगा, यदि प्राप्त डेटा में विषम संख्या है। इसका मतलब है, प्राप्त आंकड़ों में कोई त्रुटि नहीं है। यह विषम समता चेक बिट एक होगा, यदि प्राप्त डेटा में सम संख्या वाले होते हैं। इसका मतलब है, प्राप्त डेटा में कोई त्रुटि है।
समान समता चेकर को लागू करने के लिए समता चेकर की समान प्रक्रिया का पालन करें। circuit diagram विषम समता चेकर निम्नलिखित आकृति में दिखाया गया है।

उपरोक्त सर्किट आरेख में पहले स्तर में Ex-OR द्वार और दूसरे स्तर में Ex-NOR गेट हैं। चूंकि विषम समता सम समता के ठीक विपरीत है, इसलिए हम समता चेकर के आउटपुट पर एक इन्वर्टर लगा सकते हैं। उस स्थिति में, पहले, दूसरे और तीसरे स्तर में क्रमशः दो पूर्व या द्वार, एक पूर्व या द्वार और एक पलटनेवाला होता है।
द्विआधारी योजक
सबसे बुनियादी अंकगणितीय ऑपरेशन इसके अतिरिक्त है। सर्किट, जो दो द्विआधारी संख्याओं को जोड़ने का कार्य करता है, के रूप में जाना जाता हैBinary adder। सबसे पहले, हम एक योजक को लागू करते हैं, जो दो बिट्स को जोड़ने का कार्य करता है।
आधा योजक
आधा योजक एक संयोजन सर्किट है, जो दो बाइनरी संख्याओं के जोड़ देता है जो ए और बी के हैं single bit। यह दो आउटपुट योग, S & carry, C का उत्पादन करता है।
Truth table आधा योजक नीचे दिखाया गया है।
| इनपुट | आउटपुट | ||
|---|---|---|---|
| ए | ख | सी | रों |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
जब हम दो बिट्स को जोड़ते हैं, तो परिणामी योग में दशमलव में 0 से 2 तक के मान हो सकते हैं। हम बाइनरी में एकल बिट के साथ दशमलव अंक 0 और 1 का प्रतिनिधित्व कर सकते हैं। लेकिन, हम द्विआधारी में सिंगल बिट के साथ दशमलव अंक 2 का प्रतिनिधित्व नहीं कर सकते। तो, हमें बाइनरी में इसका प्रतिनिधित्व करने के लिए दो बिट्स की आवश्यकता होती है।
मान लीजिए, S, S कम से कम महत्वपूर्ण है और कै, परिणामी राशि का सबसे महत्वपूर्ण बिट है। इनपुट, कैरी, सी के पहले तीन संयोजनों के लिए, सी शून्य है और एस के मूल्य या तो शून्य या एक के आधार पर होंगेnumber of onesइनपुट्स पर मौजूद लेकिन, इनपुट के अंतिम संयोजन के लिए, कैरी, सी एक और राशि है, एस शून्य है, क्योंकि परिणामी राशि दो है।
ट्रुथ टेबल से, हम सीधे लिख सकते हैं Boolean functions के रूप में प्रत्येक उत्पादन के लिए
$$S=A \oplus B$$
$C=AB$
हम 2-इनपुट Ex-OR गेट और 2-इनपुट और गेट के साथ उपरोक्त कार्यों को लागू कर सकते हैं। circuit diagram निम्न योजक को निम्न आकृति में दिखाया गया है।

उपरोक्त सर्किट में, एक दो इनपुट पूर्व या गेट और दो इनपुट और गेट क्रमशः योग, एस एंड कैरी, सी का उत्पादन करते हैं। इसलिए, अर्ध-योजक दो बिट्स को जोड़ने का कार्य करता है।
पूर्ण योजक
पूर्ण योजक एक संयोजन सर्किट है, जो प्रदर्शन करता है addition of three bitsए, बी और सी में । कहाँ, ए एंड बी दो समानांतर महत्वपूर्ण बिट और सी हैं में कैरी सा है, जो पिछले चरण से उत्पन्न होता है है। यह पूर्ण योजक भी दो आउटपुट योग, एस एंड कैरी, सी आउट का उत्पादन करता है , जो आधे योजक के समान हैं।
Truth table पूर्ण योजक के नीचे दिखाया गया है।
| इनपुट | आउटपुट | |||
|---|---|---|---|---|
| A | B | Cin | Cout | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
जब हम तीन बिट्स को जोड़ते हैं, तो परिणामी योग में दशमलव में 0 से 3 तक के मान हो सकते हैं। हम बाइनरी में एकल बिट के साथ दशमलव अंक 0 और 1 का प्रतिनिधित्व कर सकते हैं। लेकिन, हम दशमलव अंकों 2 और 3 को द्विआधारी में एकल बिट के साथ नहीं दिखा सकते हैं। तो, हमें बाइनरी में उन दो दशमलव अंकों का प्रतिनिधित्व करने के लिए दो बिट्स की आवश्यकता होती है।
मान लीजिए, S, S कम से कम महत्वपूर्ण बिट है और कैरी, C आउट परिणामी राशि का सबसे महत्वपूर्ण बिट है। सत्य तालिका में इनपुट के सभी संयोजनों के लिए आउटपुट के मूल्यों को भरना आसान है। बस गिनती हैnumber of onesइनपुट पर मौजूद और आउटपुट पर बराबर बाइनरी नंबर लिखें। तो सी में शून्य के बराबर है, तो पूर्ण योजक सच्चाई तालिका आधा योजक सच तालिका के समान ही है।
हम निम्नलिखित प्राप्त करेंगे Boolean functions सरलीकरण के बाद प्रत्येक आउटपुट के लिए।
$$S=A \oplus B \oplus C_{in}$$
$c_{out} = AB + \left ( A \oplus B \right )c_{in}$
सम, एस एक के बराबर है, जब इनपुट पर मौजूद विषम संख्या। हम जानते हैं कि Ex-OR फाटक एक आउटपुट का उत्पादन करता है, जो एक विषम कार्य है। तो, हम या तो दो 2input पूर्व या फाटक या एक 3-इनपुट पूर्व या राशि का उत्पादन करने के लिए गेट का उपयोग कर सकते, एस हम कैरी, सी लागू कर सकते हैं बाहर दो 2input और फाटक और एक या गेट का उपयोग कर। circuit diagram पूर्ण योजक निम्न आकृति में दिखाया गया है।
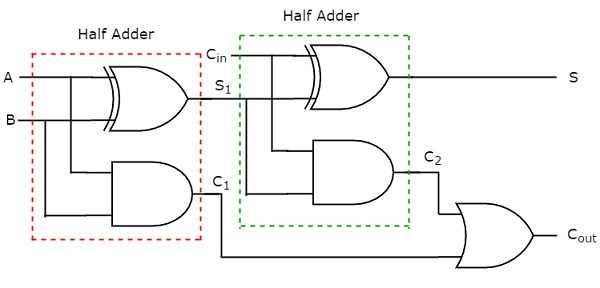
इस योजक को कहा जाता है Full adderक्योंकि एक पूर्ण योजक को लागू करने के लिए, हमें दो हाफ योजक और एक OR गेट की आवश्यकता होती है। सी हैं में शून्य है, तो पूर्ण योजक आधा योजक हो जाता है। हम इसे उपरोक्त सर्किट आरेख या पूर्ण योजक के आउटपुट के बूलियन कार्यों से आसानी से सत्यापित कर सकते हैं।
4-बिट बाइनरी एडडर
4-बिट बाइनरी योजक करता है addition of two 4-bit numbers। 4-बिट बाइनरी नंबर दें,$A=A_{3}A_{2}A_{1}A_{0}$ तथा $B= B_{3}B_{2}B_{1}B_{0}$। हम निम्नलिखित दो तरीकों में से एक में 4-बिट बाइनरी योजक को लागू कर सकते हैं।
तीन उच्च महत्वपूर्ण बिट्स के अलावा करने के लिए दो कम से कम महत्वपूर्ण बिट्स और तीन पूर्ण योजक करने के लिए एक आधे योजक का उपयोग करें।
एकरूपता के लिए चार पूर्ण योजक का उपयोग करें। के बाद से, प्रारंभिक कैरी सी में शून्य, पूर्ण योजक जो कम से कम महत्वपूर्ण बिट जोड़ने के लिए इस्तेमाल किया जाता है आधा योजक हो जाता है।
कुछ समय के लिए, हमने दूसरे दृष्टिकोण पर विचार किया। block diagram 4-बिट बाइनरी योजक को निम्न आकृति में दिखाया गया है।

यहां, 4 पूर्ण योजक कैस्केड किए जाते हैं। प्रत्येक पूर्ण योजक को दो समानांतर इनपुट A & B के संबंधित बिट्स मिल रहे हैं। एक पूर्ण योजक का कैरी आउटपुट बाद के उच्चतर ऑर्डर फुल एडियर का इनपुट होगा। यह 4-बिट बाइनरी योजक परिणामी राशि का उत्पादन करता है जिसमें अधिकांश 5 बिट्स होते हैं। तो, अंतिम चरण से बाहर ले जाने के लिए पूर्ण योजक MSB होगा।
इस तरह, हम किसी भी उच्च क्रम बाइनरी योजक को केवल पूर्ण योजक की आवश्यक संख्या को लागू करके लागू कर सकते हैं। इस बाइनरी योजक को भी कहा जाता हैripple carry (binary) adder क्योंकि कैरी एक चरण से अगले चरण तक फैलता है (तरंग)।
बाइनरी सबट्रैक्टर
सर्किट, जो दो बाइनरी संख्याओं के घटाव को करता है, के रूप में जाना जाता है Binary subtractor। हम बाइनरी सबट्रैक्टर को दो तरीकों से लागू कर सकते हैं।
- कैस्केड पूर्ण सबट्रैक्टर
- 2 की पूरक विधि
पहली विधि में, हमें 'n' पूर्ण सबट्रैक्टर को कैस्केडिंग करके एक एन-बिट बाइनरी सबट्रैक्टर मिलेगा। तो, पहले आप हाफ सबट्रैक्टर और फुल सबट्रैक्टर को लागू कर सकते हैं, हाफ योजक और पूर्ण योजक के समान। फिर, आप 'n' फुल सबट्रैक्टर को कैस्केडिंग करके एक n-बिट बाइनरी सबट्रैक्टर को लागू कर सकते हैं। तो, हमारे पास बाइनरी जोड़ और दो बाइनरी संख्याओं के घटाव के लिए दो अलग-अलग सर्किट होंगे।
दूसरी विधि में, हम केवल दूसरे इनपुट में कुछ संशोधन करके दो बाइनरी संख्याओं को घटाने के लिए एक ही बाइनरी योजक का उपयोग कर सकते हैं। इसलिए, आंतरिक रूप से द्विआधारी जोड़ ऑपरेशन होता है लेकिन, आउटपुट परिणामी घटाव है।
हम जानते हैं कि दो बाइनरी संख्या A & B का घटाव इस प्रकार लिखा जा सकता है,
$$A-B = A+\left ( {2}'s \: compliment \: of \: B \right )$$
$\Rightarrow A-B = A+\left ( {1}'s \: compliment \: of \: B \right )+1$
4-बिट बाइनरी सबट्रैक्टर
4-बिट बाइनरी सबट्रैक्टर का उत्पादन करता है subtraction of two 4-bit numbers। 4 बिट बाइनरी नंबर दें,$A=A_{3}A_{2}A_{1}A_{0}$ तथा $B= B_{3}B_{2}B_{1}B_{0}$। आंतरिक रूप से, 4-बिट बाइनरी सबट्रैक्टर का संचालन 4-बिट बाइनरी योजक के समान है। यदि बाइनरी नंबर ए के सामान्य बिट्स, बाइनरी नंबर बी के पूरक बिट्स और प्रारंभिक कैरी (उधार), सी के रूप में एक को 4-बिट बाइनरी योजक पर लागू किया जाता है, तो यह 4-बिट बाइनरी सबट्रैक्टर बन जाता है। block diagram 4-बिट बाइनरी सबट्रैक्टर को निम्न आकृति में दिखाया गया है।

यह 4-बिट बाइनरी सबट्रैक्टर एक आउटपुट उत्पन्न करता है, जो कि अधिकतम 5 बिट्स पर होता है। यदि बाइनरी नंबर ए बाइनरी नंबर बी से अधिक है, तो आउटपुट का एमएसबी शून्य है और शेष बिट्स एबी की परिमाण को पकड़ते हैं। यदि बाइनरी नंबर ए बाइनरी नंबर बी से कम है, तो आउटपुट का एमएसबी एक है। तो, एबी के परिमाण को प्राप्त करने के लिए आउटपुट के 2 पूरक लें।
इस तरह, हम किसी भी उच्च क्रम बाइनरी सबट्रैक्टर को आवश्यक संशोधनों के साथ पूर्ण योजक की आवश्यक संख्या को लागू करके लागू कर सकते हैं।
द्विआधारी योजक / घटाव
सर्किट, जिसका उपयोग किसी भी समय दो बाइनरी संख्याओं के जोड़ या घटाव के रूप में किया जा सकता है Binary Adder / subtractor। दोनों, बाइनरी योजक और बाइनरी सबट्रैक्टर में पूर्ण योजक का एक सेट होता है, जिसे कैस्केड किया जाता है। बाइनरी नंबर ए के इनपुट बिट्स सीधे बाइनरी एडिटर और बाइनरी सबट्रैक्टर दोनों में लागू होते हैं।
पूर्ण योजक के इनपुट में दो अंतर हैं जो बाइनरी योजक और बाइनरी सबट्रैक्टर में मौजूद हैं।
बाइनरी नंबर बी के इनपुट बिट्स सीधे बाइनरी एडिटर में फुल एडरों पर लागू होते हैं, जबकि बाइनरी नंबर बी के पूरक बिट्स बाइनरी सबट्रैक्टर में फुल एडरों पर लागू होते हैं।
प्रारंभिक कैरी, C 0 = 0 को 4-बिट बाइनरी योजक में लागू किया जाता है, जबकि प्रारंभिक कैरी (उधार), C 0 = 1 को 4-बिट बाइनरी सबट्रैक्टर में लागू किया जाता है।
हम जानते हैं कि ए 2-input Ex-OR gateएक आउटपुट पैदा करता है, जो पहले इनपुट के समान है जब अन्य इनपुट शून्य है। इसी तरह, यह एक आउटपुट का उत्पादन करता है, जो पहले इनपुट का पूरक होता है जब अन्य इनपुट एक होता है।
इसलिए, हम बाइनरी नंबर बी के इनपुट बिट्स को 2-इनपुट एक्स-या गेट्स पर लागू कर सकते हैं। इन सभी Ex-OR गेट्स का अन्य इनपुट C 0 है । इसलिए, सी 0 के मूल्य के आधार पर , पूर्व या द्वार द्विपदीय संख्या बी के सामान्य या पूरक बिट्स का उत्पादन करते हैं।
4-बिट बाइनरी एडडर / सबट्रैक्टर
4-बिट बाइनरी योजक / सबट्रैक्टर प्रारंभिक कैरी या उधार, 0 के मूल्य के आधार पर दो 4-बिट संख्याओं के जोड़ या घटाव का उत्पादन करता है । 4-बिट बाइनरी नंबर दें,$A=A_{3}A_{2}A_{1}A_{0}$ तथा $B= B_{3}B_{2}B_{1}B_{0}$। 4-बिट बाइनरी एडिटर / सबट्रैक्टर का संचालन 4-बिट बाइनरी एडिटर और 4-बिट बाइनरी सबट्रैक्टर के समान है।
बाइनरी संख्या ए और बी और प्रारंभिक कैरी या उधार, सी 0 के सामान्य बिट्स को बाहरी रूप से 4-बिट बाइनरी योजक में लागू करें। block diagram 4-बिट बाइनरी योजक / घटाव निम्न आकृति में दिखाया गया है।
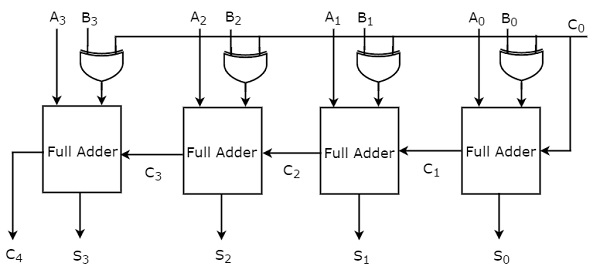
यदि प्रारंभिक कैरी, 0 शून्य है, तो प्रत्येक पूर्ण योजक को बाइनरी संख्या A & B. के सामान्य बिट्स मिलते हैं, इसलिए 4-बिट बाइनरी योजक / घटाव एक आउटपुट का उत्पादन करता है, जो किaddition of two binary numbers ए और बी।
यदि प्रारंभिक उधार, 0 एक है, तो प्रत्येक पूर्ण योजक को बाइनरी नंबर ए के सामान्य बिट्स मिलते हैं और बाइनरी नंबर बी के पूरक बिट्स। इसलिए, 4-बिट बाइनरी योजक / घटाव एक आउटपुट का उत्पादन करता है, जो किsubtraction of two binary numbers ए और बी।
इसलिए, अतिरिक्त एक्स-ओआर गेट्स की मदद से, एक ही सर्किट का उपयोग दो बाइनरी संख्याओं के जोड़ और घटाव के लिए किया जा सकता है।
Decoderएक संयोजन सर्किट है जिसमें 'n' इनपुट लाइनें और अधिकतम 2 n आउटपुट लाइनें हैं। इन आउटपुटों में से एक सक्रिय होगा उच्च मौजूद इनपुट के संयोजन के आधार पर, जब डिकोडर सक्षम होता है। इसका मतलब है कि डिकोडर एक विशेष कोड का पता लगाता है। डिकोडर के आउटपुट कुछ और नहीं हैंmin terms सक्षम होने पर, 'n' इनपुट चर (लाइनें)।
2 से 4 विकोडक
आज्ञा दें 2 से 4 विकोडक में दो इनपुट ए 1 और ए 0 और चार आउटपुट वाई 3 , वाई 2 , वाई 1 और वाई 0 हैं । block diagram 2 से 4 डीकोडर निम्नलिखित आकृति में दिखाया गया है।

सक्षम होने पर इनपुट के प्रत्येक संयोजन के लिए इन चार आउटपुटों में से एक '1' होगा। Truth table 2 से 4 डीकोडर नीचे दिखाया गया है।
| सक्षम | इनपुट | आउटपुट | ||||
|---|---|---|---|---|---|---|
| E | A1 | A0 | Y3 | Y2 | Y1 | Y0 |
| 0 | एक्स | एक्स | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 |
ट्रुथ टेबल से, हम लिख सकते हैं Boolean functions के रूप में प्रत्येक उत्पादन के लिए
$$Y_{3}=E.A_{1}.A_{0}$$
$$ Y_{2}=E.A_{1}.{A_{0}}'$$
$$ Y_{1}=E.{A_{1}}'.A_{0}$$
$$ Y_{0}=E.{A_{1}}'.{A_{0}}'$$
प्रत्येक आउटपुट में एक उत्पाद अवधि होती है। तो, कुल चार उत्पाद शब्द हैं। हम चार और गेट्स का उपयोग करके इन चार उत्पाद शर्तों को लागू कर सकते हैं जिनमें प्रत्येक और दो इनवर्टर के तीन इनपुट हैं। circuit diagram 2 से 4 डीकोडर निम्नलिखित आकृति में दिखाया गया है।

इसलिए, 2 से 4 डीकोडर के आउटपुट कुछ और नहीं हैं min termsदो इनपुट चर ए 1 और ए 0 में , जब सक्षम होता है, तो ई एक के बराबर होता है। यदि सक्षम है, ई शून्य है, तो डिकोडर के सभी आउटपुट शून्य के बराबर होंगे।
इसी तरह, 3 से 8 डिकोडर तीन इनपुट चर ए 2 , ए 1 और ए 0 और आठ से 16 डिकोडर के आठ मिनट का उत्पादन करते हैं, चार इनपुट चर ए 3 , ए 2 , ए 1 और ए 0 के सोलह मिनट शब्द पैदा करते हैं ।
उच्च-क्रम के डिकोडर्स का कार्यान्वयन
अब, निम्न-क्रम डिकोडर्स का उपयोग करके निम्नलिखित दो उच्च-क्रम डिकोडर्स को लागू करते हैं।
- 3 से 8 डिकोडर
- 4 से 16 डिकोडर
3 से 8 विकोडक
इस भाग में, हम लागू करते हैं 3 to 8 decoder using 2 to 4 decoders। हम जानते हैं कि 2 से 4 डिकोडर में दो इनपुट होते हैं, ए 1 और ए 0 और चार आउटपुट, वाई 3 से वाई 0 । जबकि, 3 से 8 डिकोडर में तीन इनपुट ए 2 , ए 1 और ए 0 और आठ आउटपुट, वाई 7 से वाई 0 हैं ।
हम निम्न आदेश डिकोडर को निम्न सूत्र का उपयोग करके उच्च आदेश डिकोडर को लागू करने के लिए आवश्यक पा सकते हैं।
$$Required \: number \: of \: lower \: order \: decoders=\frac{m_{2}}{m_{1}}$$
कहाँ पे,
$m_{1}$ निचले क्रम के डिकोडर के आउटपुट की संख्या है।
$m_{2}$ उच्च आदेश डिकोडर के आउटपुट की संख्या है।
यहाँ, $m_{1}$ = 4 और $m_{2}$ = 8. उपर्युक्त सूत्र में ये दो मान हैं।
$$Required \: number \: of \: 2 \: to \: 4 \: decoders=\frac{8}{4}=2$$
इसलिए, हमें एक 3 से 8 डिकोडर को लागू करने के लिए दो 2 से 4 डिकोडर्स की आवश्यकता होती है। block diagram 3 से 8 डिकोडर में 2 से 4 डेकोडर का उपयोग करके निम्नलिखित आकृति में दिखाया गया है।

समानांतर इनपुट ए 1 और ए 0 प्रत्येक 2 से 4 डिकोडर पर लागू होते हैं। इनपुट ए 2 का पूरक आउटपुट, वाई 3 से वाई 0 पाने के लिए सक्षम 2 से 4 डीकोडर के ई से जुड़ा है । ये हैंlower four min terms। इनपुट, ए 2 आउटपुट, वाई 7 से वाई 4 तक पाने के लिए, सीधे 2 से 4 डिकोडर के ई, सक्षम से जुड़ा हुआ है । ये हैंhigher four min terms।
4 से 16 विकोडक
इस भाग में, हम लागू करते हैं 4 to 16 decoder using 3 to 8 decoders। हम जानते हैं कि 3 से 8 विकोडक में तीन इनपुट ए 2 , ए 1 और ए 0 और आठ आउटपुट, वाई 7 से वाई 0 हैं । जबकि, 4 से 16 डिकोडर में चार इनपुट ए 3 , ए 2 , ए 1 और ए 0 और सोलह आउटपुट, वाई 15 से वाई 0 है।
निम्न आदेश डिकोडर की आवश्यकता को खोजने के लिए हम निम्न सूत्र को जानते हैं।
$$Required \: number \: of \: lower \: order \: decoders=\frac{m_{2}}{m_{1}}$$
विकल्प, $m_{1}$ = 8 और $m_{2}$ = उपरोक्त सूत्र में १६।
$$Required \: number \: of \: 3 \: to \: 8 decoders=\frac{16}{8}=2$$
इसलिए, हमें एक 4 से 16 डिकोडर को लागू करने के लिए दो 3 से 8 डीकोडर्स की आवश्यकता होती है। block diagram 3 से 8 डीकोडर्स का उपयोग करके 4 से 16 डिकोडर को निम्न आकृति में दिखाया गया है।

समानांतर इनपुट A 2 , A 1 & A 0 प्रत्येक 3 से 8 डिकोडर पर लागू होते हैं। इनपुट का पूरक, ए 3 आउटपुट, वाई 7 से वाई 0 पाने के लिए, कम से कम 3 से 8 डीकोडर के ई से जुड़ा है । ये हैंlower eight min terms। इनपुट, ए 3 सीधे आउटपुट से कनेक्ट करने के लिए, ऊपरी 3 से 8 डिकोडर के ई, आउटपुट 15 , वाई 15 से वाई 8 तक जुड़ा हुआ है । ये हैंhigher eight min terms।
एक Encoderएक दहनशील सर्किट है जो डिकोडर के रिवर्स ऑपरेशन करता है। इसमें अधिकतम 2 n इनपुट लाइनें और 'n' आउटपुट लाइनें हैं। यह इनपुट के बराबर एक बाइनरी कोड का उत्पादन करेगा, जो सक्रिय उच्च है। इसलिए, एनकोडर 'एन' बिट्स के साथ 2 एन इनपुट लाइनों को एनकोड करता है । यह एनकोडर में सक्षम सिग्नल का प्रतिनिधित्व करने के लिए वैकल्पिक है।
4 से 2 एनकोडर
आज्ञा दें 4 से 2 एनकोडर में चार इनपुट हैं Y 3 , Y 2 , Y 1 और Y 0 और दो आउटपुट A 1 & A 0 । block diagram 4 से 2 एनकोडर को निम्न आकृति में दिखाया गया है।

किसी भी समय, आउटपुट में संबंधित बाइनरी कोड प्राप्त करने के लिए इन 4 इनपुटों में से केवल एक ही '1' हो सकता है। Truth table 4 से 2 एनकोडर नीचे दिखाया गया है।
| इनपुट | आउटपुट | ||||
|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
ट्रुथ टेबल से, हम लिख सकते हैं Boolean functions के रूप में प्रत्येक उत्पादन के लिए
$$A_{1}=Y_{3}+Y_{2}$$
$$A_{0}=Y_{3}+Y_{1}$$
हम दो इनपुट या गेट का उपयोग करके उपरोक्त दो बूलियन कार्यों को लागू कर सकते हैं। circuit diagram 4 से 2 एनकोडर को निम्न आकृति में दिखाया गया है।

उपरोक्त सर्किट आरेख में दो या द्वार हैं। ये या गेट दो बिट्स के साथ चार इनपुट को एन्कोड करते हैं
ऑक्टल टू बाइनरी एनकोडर
ऑक्टल टू बाइनरी एनकोडर में आठ इनपुट, वाई 7 से वाई 0 और तीन आउटपुट ए 2 , ए 1 और ए 0 हैं । ऑक्टल टू बाइनरी एनकोडर कुछ नहीं बल्कि 8 से 3 एनकोडर है। block diagram ऑक्टल टू बाइनरी एनकोडर को निम्न आकृति में दिखाया गया है।
किसी भी समय, संबंधित बाइनरी कोड प्राप्त करने के लिए इन आठ इनपुटों में से केवल एक ही '1' हो सकता है। Truth table ऑक्टल से बाइनरी एनकोडर को नीचे दिखाया गया है।
| इनपुट | आउटपुट | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
ट्रुथ टेबल से, हम लिख सकते हैं Boolean functions के रूप में प्रत्येक उत्पादन के लिए
$$A_{2}=Y_{7}+Y_{6}+Y_{5}+Y_{4}$$
$$A_{1}=Y_{7}+Y_{6}+Y_{3}+Y_{2}$$
$$A_{0}=Y_{7}+Y_{5}+Y_{3}+Y_{1}$$
हम चार इनपुट या गेट्स का उपयोग करके उपरोक्त बूलियन कार्यों को लागू कर सकते हैं। circuit diagram ऑक्टल टू बाइनरी एनकोडर को निम्न आकृति में दिखाया गया है।

उपरोक्त सर्किट आरेख में तीन 4-इनपुट या गेट शामिल हैं। ये या गेट्स तीन बिट्स के साथ आठ इनपुट को एन्कोड करते हैं।
एनकोडर की कमियां
निम्नलिखित सामान्य एनकोडर की कमियां हैं।
एक अस्पष्टता है, जब एनकोडर के सभी आउटपुट शून्य के बराबर हैं। क्योंकि, यह इनपुट के अनुरूप कोड हो सकता है, जब केवल कम से कम महत्वपूर्ण इनपुट एक हो या जब सभी इनपुट शून्य हों।
यदि एक से अधिक इनपुट सक्रिय उच्च है, तो एनकोडर एक आउटपुट का उत्पादन करता है, जो सही कोड नहीं हो सकता है। के लियेexample, यदि Y 3 और Y 6 दोनों '1' हैं, तो आउटपुट पर एनकोडर 111 पैदा करता है। यह न तो Y 3 के समतुल्य कोड है , जब यह '1' है और न ही Y 6 के समतुल्य कोड , जब यह '1' है।
इसलिए, इन कठिनाइयों को दूर करने के लिए, हमें एनकोडर के प्रत्येक इनपुट को प्राथमिकताएं देनी चाहिए। फिर, एनकोडर का आउटपुट सक्रिय उच्च इनपुट (एस) के अनुरूप (बाइनरी) कोड होगा, जिसमें उच्च प्राथमिकता है। इस एनकोडर को कहा जाता हैpriority encoder।
प्राथमिकता एनकोडर
4 से 2 प्राथमिकता वाले एनकोडर में चार इनपुट वाई 3 , वाई 2 , वाई 1 और वाई 0 और दो आउटपुट ए 1 और ए 0 हैं । यहां, इनपुट, वाई 3 की सर्वोच्च प्राथमिकता है, जबकि इनपुट, वाई 0 की सबसे कम प्राथमिकता है। इस स्थिति में, भले ही एक से अधिक इनपुट '1' हो, लेकिन आउटपुट इनपुट के अनुरूप (बाइनरी) कोड होगा,higher priority।
हमने एक और विचार किया output, V यह जानने के लिए कि आउटपुट में उपलब्ध कोड वैध है या नहीं।
यदि एनकोडर का कम से कम एक इनपुट '1' है, तो आउटपुट पर उपलब्ध कोड एक मान्य है। इस मामले में, आउटपुट, वी 1 के बराबर होगा।
यदि एनकोडर के सभी इनपुट '0' हैं, तो आउटपुट पर उपलब्ध कोड मान्य नहीं है। इस मामले में, आउटपुट, V 0 के बराबर होगा।
Truth table 4 से 2 प्राथमिकता एनकोडर नीचे दिखाया गया है।
| इनपुट | आउटपुट | |||||
|---|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 | V |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | एक्स | 0 | 1 | 1 |
| 0 | 1 | एक्स | एक्स | 1 | 0 | 1 |
| 1 | एक्स | एक्स | एक्स | 1 | 1 | 1 |
उपयोग 4 variable K-maps प्रत्येक आउटपुट के लिए सरल अभिव्यक्ति प्राप्त करने के लिए।
सरलीकृत किया गया Boolean functions कर रहे हैं
$$A_{1}=Y_{3}+Y_{2}$$
$A_{0}=Y_{3}+{Y_{2}}'Y_{1}$
इसी तरह, हम आउटपुट के बूलियन फ़ंक्शन को प्राप्त करेंगे, वी के रूप में
$$V=Y_{3}+Y_{2}+Y_{1}+Y_{0}$$
हम तर्क फाटकों का उपयोग करके उपरोक्त बूलियन कार्यों को लागू कर सकते हैं। circuit diagram 4 से 2 प्राथमिकता एनकोडर निम्नलिखित आकृति में दिखाया गया है।

उपरोक्त सर्किट आरेख में दो 2-इनपुट या गेट, एक 4-इनपुट या गेट, एक 2input और गेट और एक इन्वर्टर शामिल हैं। यहां और गेट और इन्वर्टर संयोजन का उपयोग आउटपुट पर एक वैध कोड बनाने के लिए किया जाता है, यहां तक कि जब एक ही समय में कई इनपुट '1' के बराबर होते हैं। इसलिए, यह सर्किट दो बिट्स के साथ चार इनपुट को इनकोड करता हैpriority प्रत्येक इनपुट को सौंपा।
Multiplexerएक संयोजन सर्किट है जिसमें अधिकतम 2 n डेटा इनपुट, 'n' चयन लाइनें और एकल आउटपुट लाइन है। इनमें से एक डेटा इनपुट चयन लाइनों के मूल्यों के आधार पर आउटपुट से जुड़ा होगा।
चूंकि 'एन' चयन लाइनें हैं, इसलिए शून्य और लोगों के 2 एन संभव संयोजन होंगे। इसलिए, प्रत्येक संयोजन केवल एक डेटा इनपुट का चयन करेगा। मल्टीप्लेक्सर भी कहा जाता हैMux।
4x1 मल्टीप्लेक्स
4x1 मल्टीप्लेक्स में चार डेटा इनपुट I 3 , I 2 , I 1 और I 0 , दो चयन लाइनें s 1 & s 0 और एक आउटपुट Y है।block diagram 4x1 का मल्टीप्लेक्स निम्न आकृति में दिखाया गया है।

इन 4 में से एक इनपुट इन दो चयन लाइनों पर मौजूद इनपुट के संयोजन के आधार पर आउटपुट से जुड़ा होगा। Truth table 4x1 का मल्टीप्लेक्स नीचे दिखाया गया है।
| चयन लाइनें | उत्पादन | |
|---|---|---|
| S1 | S0 | Y |
| 0 | 0 | मैं ० |
| 0 | 1 | मैं १ |
| 1 | 0 | मैं २ |
| 1 | 1 | मैं ३ |
ट्रुथ टेबल से, हम सीधे लिख सकते हैं Boolean function आउटपुट के लिए, वाई के रूप में
$$Y={S_{1}}'{S_{0}}'I_{0}+{S_{1}}'S_{0}I_{1}+S_{1}{S_{0}}'I_{2}+S_{1}S_{0}I_{3}$$
हम इनवर्टर और गेट्स या OR गेट का उपयोग करके इस बूलियन फ़ंक्शन को लागू कर सकते हैं। circuit diagram of 4x1 multiplexer is shown in the following figure.

We can easily understand the operation of the above circuit. Similarly, you can implement 8x1 Multiplexer and 16x1 multiplexer by following the same procedure.
Implementation of Higher-order Multiplexers.
Now, let us implement the following two higher-order Multiplexers using lower-order Multiplexers.
- 8x1 Multiplexer
- 16x1 Multiplexer
8x1 Multiplexer
In this section, let us implement 8x1 Multiplexer using 4x1 Multiplexers and 2x1 Multiplexer. We know that 4x1 Multiplexer has 4 data inputs, 2 selection lines and one output. Whereas, 8x1 Multiplexer has 8 data inputs, 3 selection lines and one output.
So, we require two 4x1 Multiplexers in first stage in order to get the 8 data inputs. Since, each 4x1 Multiplexer produces one output, we require a 2x1 Multiplexer in second stage by considering the outputs of first stage as inputs and to produce the final output.
Let the 8x1 Multiplexer has eight data inputs I7 to I0, three selection lines s2, s1 & s0 and one output Y. The Truth table of 8x1 Multiplexer is shown below.
| Selection Inputs | Output | ||
|---|---|---|---|
| S2 | S1 | S0 | Y |
| 0 | 0 | 0 | I0 |
| 0 | 0 | 1 | I1 |
| 0 | 1 | 0 | I2 |
| 0 | 1 | 1 | I3 |
| 1 | 0 | 0 | I4 |
| 1 | 0 | 1 | I5 |
| 1 | 1 | 0 | I6 |
| 1 | 1 | 1 | I7 |
We can implement 8x1 Multiplexer using lower order Multiplexers easily by considering the above Truth table. The block diagram of 8x1 Multiplexer is shown in the following figure.

The same selection lines, s1 & s0 are applied to both 4x1 Multiplexers. The data inputs of upper 4x1 Multiplexer are I7 to I4 and the data inputs of lower 4x1 Multiplexer are I3 to I0. Therefore, each 4x1 Multiplexer produces an output based on the values of selection lines, s1 & s0.
The outputs of first stage 4x1 Multiplexers are applied as inputs of 2x1 Multiplexer that is present in second stage. The other selection line, s2 is applied to 2x1 Multiplexer.
If s2 is zero, then the output of 2x1 Multiplexer will be one of the 4 inputs I3 to I0 based on the values of selection lines s1 & s0.
If s2 is one, then the output of 2x1 Multiplexer will be one of the 4 inputs I7 to I4 based on the values of selection lines s1 & s0.
Therefore, the overall combination of two 4x1 Multiplexers and one 2x1 Multiplexer performs as one 8x1 Multiplexer.
16x1 Multiplexer
In this section, let us implement 16x1 Multiplexer using 8x1 Multiplexers and 2x1 Multiplexer. We know that 8x1 Multiplexer has 8 data inputs, 3 selection lines and one output. Whereas, 16x1 Multiplexer has 16 data inputs, 4 selection lines and one output.
So, we require two 8x1 Multiplexers in first stage in order to get the 16 data inputs. Since, each 8x1 Multiplexer produces one output, we require a 2x1 Multiplexer in second stage by considering the outputs of first stage as inputs and to produce the final output.
Let the 16x1 Multiplexer has sixteen data inputs I15 to I0, four selection lines s3 to s0 and one output Y. The Truth table of 16x1 Multiplexer is shown below.
| Selection Inputs | Output | |||
|---|---|---|---|---|
| S3 | S2 | S1 | S0 | Y |
| 0 | 0 | 0 | 0 | I0 |
| 0 | 0 | 0 | 1 | I1 |
| 0 | 0 | 1 | 0 | I2 |
| 0 | 0 | 1 | 1 | I3 |
| 0 | 1 | 0 | 0 | I4 |
| 0 | 1 | 0 | 1 | I5 |
| 0 | 1 | 1 | 0 | I6 |
| 0 | 1 | 1 | 1 | I7 |
| 1 | 0 | 0 | 0 | I8 |
| 1 | 0 | 0 | 1 | I9 |
| 1 | 0 | 1 | 0 | I10 |
| 1 | 0 | 1 | 1 | I11 |
| 1 | 1 | 0 | 0 | I12 |
| 1 | 1 | 0 | 1 | I13 |
| 1 | 1 | 1 | 0 | I14 |
| 1 | 1 | 1 | 1 | I15 |
We can implement 16x1 Multiplexer using lower order Multiplexers easily by considering the above Truth table. The block diagram of 16x1 Multiplexer is shown in the following figure.

The same selection lines, s2, s1 & s0 are applied to both 8x1 Multiplexers. The data inputs of upper 8x1 Multiplexer are I15 to I8 and the data inputs of lower 8x1 Multiplexer are I7 to I0. Therefore, each 8x1 Multiplexer produces an output based on the values of selection lines, s2, s1 & s0.
The outputs of first stage 8x1 Multiplexers are applied as inputs of 2x1 Multiplexer that is present in second stage. The other selection line, s3 is applied to 2x1 Multiplexer.
If s3 is zero, then the output of 2x1 Multiplexer will be one of the 8 inputs Is7 to I0 based on the values of selection lines s2, s1 & s0.
If s3 is one, then the output of 2x1 Multiplexer will be one of the 8 inputs I15 to I8 based on the values of selection lines s2, s1 & s0.
Therefore, the overall combination of two 8x1 Multiplexers and one 2x1 Multiplexer performs as one 16x1 Multiplexer.
De-Multiplexer is a combinational circuit that performs the reverse operation of Multiplexer. It has single input, ‘n’ selection lines and maximum of 2n outputs. The input will be connected to one of these outputs based on the values of selection lines.
Since there are ‘n’ selection lines, there will be 2n possible combinations of zeros and ones. So, each combination can select only one output. De-Multiplexer is also called as De-Mux.
1x4 De-Multiplexer
1x4 De-Multiplexer has one input I, two selection lines, s1 & s0 and four outputs Y3, Y2, Y1 &Y0. The block diagram of 1x4 De-Multiplexer is shown in the following figure.

The single input ‘I’ will be connected to one of the four outputs, Y3 to Y0 based on the values of selection lines s1 & s0. The Truth table of 1x4 De-Multiplexer is shown below.
| Selection Inputs | Outputs | ||||
|---|---|---|---|---|---|
| S1 | S0 | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | I |
| 0 | 1 | 0 | 0 | I | 0 |
| 1 | 0 | 0 | I | 0 | 0 |
| 1 | 1 | I | 0 | 0 | 0 |
From the above Truth table, we can directly write the Boolean functions for each output as
$$Y_{3}=s_{1}s_{0}I$$
$$Y_{2}=s_{1}{s_{0}}'I$$
$$Y_{1}={s_{1}}'s_{0}I$$
$$Y_{0}={s_1}'{s_{0}}'I$$
We can implement these Boolean functions using Inverters & 3-input AND gates. The circuit diagram of 1x4 De-Multiplexer is shown in the following figure.

We can easily understand the operation of the above circuit. Similarly, you can implement 1x8 De-Multiplexer and 1x16 De-Multiplexer by following the same procedure.
Implementation of Higher-order De-Multiplexers
Now, let us implement the following two higher-order De-Multiplexers using lower-order De-Multiplexers.
- 1x8 De-Multiplexer
- 1x16 De-Multiplexer
1x8 De-Multiplexer
In this section, let us implement 1x8 De-Multiplexer using 1x4 De-Multiplexers and 1x2 De-Multiplexer. We know that 1x4 De-Multiplexer has single input, two selection lines and four outputs. Whereas, 1x8 De-Multiplexer has single input, three selection lines and eight outputs.
So, we require two 1x4 De-Multiplexers in second stage in order to get the final eight outputs. Since, the number of inputs in second stage is two, we require 1x2 DeMultiplexer in first stage so that the outputs of first stage will be the inputs of second stage. Input of this 1x2 De-Multiplexer will be the overall input of 1x8 De-Multiplexer.
Let the 1x8 De-Multiplexer has one input I, three selection lines s2, s1 & s0 and outputs Y7 to Y0. The Truth table of 1x8 De-Multiplexer is shown below.
| Selection Inputs | Outputs | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| s2 | s1 | s0 | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | I |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | I | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
We can implement 1x8 De-Multiplexer using lower order Multiplexers easily by considering the above Truth table. The block diagram of 1x8 De-Multiplexer is shown in the following figure.

The common selection lines, s1 & s0 are applied to both 1x4 De-Multiplexers. The outputs of upper 1x4 De-Multiplexer are Y7 to Y4 and the outputs of lower 1x4 De-Multiplexer are Y3 to Y0.
The other selection line, s2 is applied to 1x2 De-Multiplexer. If s2 is zero, then one of the four outputs of lower 1x4 De-Multiplexer will be equal to input, I based on the values of selection lines s1 & s0. Similarly, if s2 is one, then one of the four outputs of upper 1x4 DeMultiplexer will be equal to input, I based on the values of selection lines s1 & s0.
1x16 De-Multiplexer
In this section, let us implement 1x16 De-Multiplexer using 1x8 De-Multiplexers and 1x2 De-Multiplexer. We know that 1x8 De-Multiplexer has single input, three selection lines and eight outputs. Whereas, 1x16 De-Multiplexer has single input, four selection lines and sixteen outputs.
So, we require two 1x8 De-Multiplexers in second stage in order to get the final sixteen outputs. Since, the number of inputs in second stage is two, we require 1x2 DeMultiplexer in first stage so that the outputs of first stage will be the inputs of second stage. Input of this 1x2 De-Multiplexer will be the overall input of 1x16 De-Multiplexer.
Let the 1x16 De-Multiplexer has one input I, four selection lines s3, s2, s1 & s0 and outputs Y15 to Y0. The block diagram of 1x16 De-Multiplexer using lower order Multiplexers is shown in the following figure.
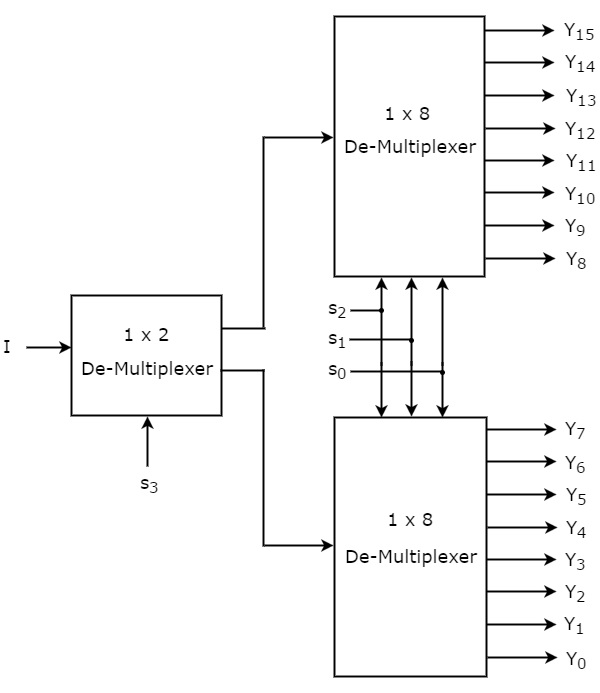
The common selection lines s2, s1 & s0 are applied to both 1x8 De-Multiplexers. The outputs of upper 1x8 De-Multiplexer are Y15 to Y8 and the outputs of lower 1x8 DeMultiplexer are Y7 to Y0.
अन्य selection line, s31x2 डी-मल्टीप्लेक्सर पर लागू होता है। यदि s 3 शून्य है, तो निम्न 1x8 De-Multiplexer के आठ आउटपुट में से एक इनपुट के बराबर होगा, मैं चयन लाइनों 2 , s 1 & s 0 के मूल्यों के आधार पर । इसी तरह, यदि s3 एक है, तो ऊपरी 1x8 De-Multiplexer के 8 आउटपुट में से एक इनपुट के बराबर होगा, मैं चयन लाइनों 2 , s 1 & s 0 के मूल्यों के आधार पर ।
प्रोग्रामेबल तर्क उपकरण (PLDs)एकीकृत सर्किट हैं। उनमें AND गेटों की एक सरणी और OR गेटों की एक और सरणी होती है। सरणी के प्रकार के आधार पर तीन प्रकार के पीएलडी हैं, जिसमें प्रोग्राम करने योग्य सुविधा है।
- प्रोग्रामेबल रीड ओनली मेमोरी
- प्रोग्रामेबल एरे लॉजिक
- प्रोग्राम करने योग्य तर्क
इन उपकरणों में जानकारी दर्ज करने की प्रक्रिया के रूप में जाना जाता है programming। मूल रूप से, उपयोगकर्ता आवश्यकता के आधार पर बूलियन कार्यों को लागू करने के लिए इन उपकरणों या आईसी को विद्युत रूप से प्रोग्राम कर सकते हैं। यहां, प्रोग्रामिंग शब्द हार्डवेयर प्रोग्रामिंग को संदर्भित करता है, लेकिन सॉफ्टवेयर प्रोग्रामिंग को नहीं।
प्रोग्रामेबल रीड ओनली मेमोरी (PROM)
रीड ओनली मेमोरी (ROM) एक मेमोरी डिवाइस है, जो बाइनरी जानकारी को स्थायी रूप से संग्रहीत करता है। इसका मतलब है, हम उस संग्रहीत जानकारी को बाद में किसी भी तरह से बदल नहीं सकते हैं। यदि ROM में प्रोग्राम करने योग्य सुविधा है, तो इसे कहा जाता हैProgrammable ROM (PROM)। PROM प्रोग्रामर का उपयोग करके उपयोगकर्ता को एक बार बाइनरी जानकारी को विद्युत रूप से प्रोग्राम करने की सुविधा है।
PROM एक प्रोग्रामेबल लॉजिक डिवाइस है, जिसने AND और प्रोग्रामेबल या अरै तय की है। block diagram PROM को निम्न आकृति में दिखाया गया है।

यहाँ, और गेट्स के इनपुट प्रोग्राम करने योग्य प्रकार के नहीं हैं। तो, हम 2 उत्पन्न करने के लिए है n 2 का उपयोग करके उत्पाद शर्तों n और फाटक होने n आदानों प्रत्येक। हम nx2 एन डिकोडर का उपयोग करके इन उत्पाद शर्तों को लागू कर सकते हैं । तो, यह डिकोडर 'n' उत्पन्न करता हैmin terms।
यहाँ, OR गेट्स के इनपुट प्रोग्राम करने योग्य हैं। इसका मतलब है, हम किसी भी संख्या में आवश्यक उत्पाद शर्तों को प्रोग्राम कर सकते हैं, क्योंकि प्रत्येक गेट के इनपुट के रूप में AND गेट्स के सभी आउटपुट लागू होते हैं। इसलिए, PROM के आउटपुट के रूप में होगाsum of min terms।
उदाहरण
आइए हम निम्नलिखित को लागू करें Boolean functions PROM का उपयोग करना।
$$A(X,Y,Z)=\sum m\left ( 5,6,7 \right )$$
$$B(X,Y,Z)=\sum m\left ( 3,5,6,7 \right )$$
दिए गए दो कार्य न्यूनतम शर्तों के रूप में हैं और प्रत्येक फ़ंक्शन के तीन चर X, Y & Z हैं। इसलिए, हमें इन दोनों कार्यों के उत्पादन के लिए 3 से 8 डिकोडर और दो प्रोग्रामेबल या गेट्स की आवश्यकता होती है। अनुरूपPROM निम्नलिखित आकृति में दिखाया गया है।

यहां 3 से 8 डीकोडर आठ मिनट की अवधि उत्पन्न करता है। दो प्रोग्रामेबल या गेट्स के पास इन सभी मिनिमम टर्म्स की पहुंच होती है। लेकिन, प्रत्येक OR गेट द्वारा संबंधित बूलियन कार्यों का उत्पादन करने के लिए केवल आवश्यक न्यूनतम शर्तों को क्रमादेशित किया जाता है। प्रतीक 'X' का उपयोग प्रोग्रामेबल कनेक्शन के लिए किया जाता है।
प्रोग्रामेबल ऐरे लॉजिक (पाल)
PAL एक प्रोग्रामेबल लॉजिक डिवाइस है जिसमें प्रोग्रामेबल और एरे और फिक्स्ड OR सरणी है। पाल का लाभ यह है कि हम प्रोग्राम और गेट्स का उपयोग करके सभी न्यूनतम शर्तों को उत्पन्न करने के बजाय बूलियन फ़ंक्शन के केवल आवश्यक उत्पाद शब्द ही उत्पन्न कर सकते हैं। block diagram पाल के निम्नलिखित चित्र में दिखाया गया है।

यहां, AND गेट्स के इनपुट प्रोग्राम करने योग्य हैं। इसका मतलब है कि प्रत्येक और गेट में चर के सामान्य और पूरक दोनों इनपुट होते हैं। इसलिए, आवश्यकता के आधार पर, हम उन किसी भी इनपुट को प्रोग्राम कर सकते हैं। तो, हम केवल आवश्यक उत्पन्न कर सकते हैंproduct terms इन और फाटकों का उपयोग करके।
यहाँ, OR गेट्स के इनपुट प्रोग्राम करने योग्य प्रकार के नहीं हैं। तो, प्रत्येक OR गेट पर इनपुट की संख्या निश्चित प्रकार की होगी। इसलिए, उन आवश्यक उत्पाद शर्तों को इनपुट के रूप में प्रत्येक OR गेट पर लागू करें। इसलिए, पाल के आउटपुट के रूप में होगाsum of products form।
उदाहरण
आइए हम निम्नलिखित को लागू करें Boolean functions PAL का उपयोग करना।
$$A=XY+X{Z}'$$
$$A=X{Y}'+Y{Z}'$$
दिए गए दो कार्य उत्पादों के रूप में हैं। प्रत्येक बूलियन फ़ंक्शन में दो उत्पाद शब्द मौजूद हैं। इसलिए, हमें उन दो कार्यों के निर्माण के लिए चार प्रोग्रामेबल और गेट्स और दो फिक्स्ड या गेट्स की आवश्यकता है। अनुरूपPAL निम्नलिखित आकृति में दिखाया गया है।

programmable AND gatesचर के सामान्य और पूरक इनपुट दोनों की पहुंच है। उपरोक्त आकृति में, इनपुट X,${X}'$, वाई, ${Y}'$, Z & ${Z}'$, प्रत्येक और गेट के इनपुट पर उपलब्ध हैं। इसलिए, प्रत्येक और गेट द्वारा एक उत्पाद शब्द उत्पन्न करने के लिए केवल आवश्यक शाब्दिक कार्यक्रम। प्रतीक 'X' का उपयोग प्रोग्रामेबल कनेक्शन के लिए किया जाता है।
यहाँ, OR गेट्स के इनपुट निश्चित प्रकार के हैं। तो, आवश्यक उत्पाद शब्द प्रत्येक के इनपुट से जुड़े होते हैंOR gate। ताकि OR गेट्स संबंधित बूलियन फ़ंक्शन का उत्पादन करें। प्रतीक '।' निश्चित कनेक्शन के लिए उपयोग किया जाता है।
प्रोग्रामेबल तर्क सरणी (पीएलए)
पीएलए एक प्रोग्रामेबल लॉजिक डिवाइस है, जिसमें प्रोग्रामेबल और एरे और प्रोग्रामेबल या एरे दोनों ही हैं। इसलिए, यह सबसे लचीला PLD है। block diagram पीएलए को निम्न आकृति में दिखाया गया है।

यहां, AND गेट्स के इनपुट प्रोग्राम करने योग्य हैं। इसका मतलब है कि प्रत्येक और गेट में चर के सामान्य और पूरक दोनों इनपुट होते हैं। इसलिए, आवश्यकता के आधार पर, हम उन किसी भी इनपुट को प्रोग्राम कर सकते हैं। तो, हम केवल आवश्यक उत्पन्न कर सकते हैंproduct terms इन और फाटकों का उपयोग करके।
यहां, OR गेटों के इनपुट भी प्रोग्राम किए जा सकते हैं। इसलिए, हम आवश्यक उत्पाद शर्तों को किसी भी संख्या में प्रोग्राम कर सकते हैं, क्योंकि प्रत्येक गेट के इनपुट के रूप में AND गेट्स के सभी आउटपुट लागू होते हैं। इसलिए, पाल के आउटपुट के रूप में होगाsum of products form।
उदाहरण
आइए हम निम्नलिखित को लागू करें Boolean functions पीएलए का उपयोग करना।
$$A=XY+X{Z}'$$
$$B=X{Y}'+YZ+X{Z}'$$
दिए गए दो कार्य उत्पादों के रूप में हैं। दिए गए बूलियन फ़ंक्शंस में मौजूद उत्पाद शर्तों की संख्या क्रमशः दो और तीन है। एक उत्पाद अवधि,${Z}'X$ प्रत्येक फ़ंक्शन में आम है।
इसलिए, हमें उन दो कार्यों के निर्माण के लिए चार प्रोग्रामेबल और गेट्स और दो प्रोग्रामेबल या गेट्स की आवश्यकता है। अनुरूपPLA निम्नलिखित आकृति में दिखाया गया है।
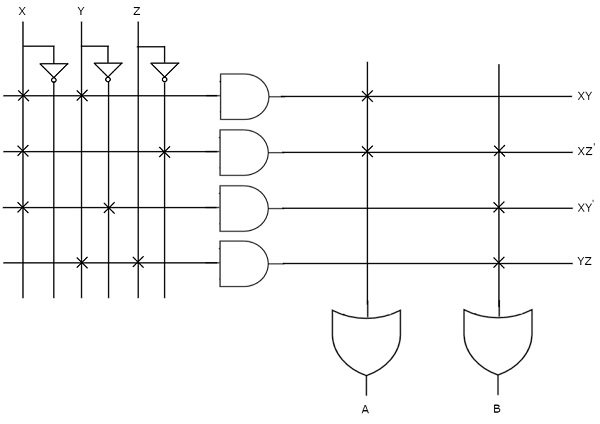
programmable AND gatesचर के सामान्य और पूरक इनपुट दोनों की पहुंच है। उपरोक्त आकृति में, इनपुट X,${X}'$, वाई, ${Y}'$, Z & ${Z}'$, प्रत्येक और गेट के इनपुट पर उपलब्ध हैं। इसलिए, प्रत्येक और गेट द्वारा एक उत्पाद शब्द उत्पन्न करने के लिए केवल आवश्यक शाब्दिक कार्यक्रम।
ये सभी उत्पाद शर्तें प्रत्येक के इनपुट पर उपलब्ध हैं programmable OR gate। लेकिन, केवल प्रत्येक OR गेट द्वारा संबंधित बूलियन फ़ंक्शन का उत्पादन करने के लिए आवश्यक उत्पाद शर्तों को प्रोग्राम करें। प्रतीक 'X' का उपयोग प्रोग्रामेबल कनेक्शन के लिए किया जाता है।
पिछले अध्यायों में, हमने लॉजिक गेट्स का उपयोग करके विभिन्न कॉम्बिनेशन सर्किट लागू किए हैं। गेट को छोड़कर, शेष सभी लॉजिक गेटों में कम से कम दो इनपुट और एकल आउटपुट हैं। इसी तरह,threshold gate इसमें कम से कम एक इनपुट और केवल एक आउटपुट शामिल है।
इसके अतिरिक्त, इसमें प्रत्येक इनपुट और थ्रेशोल्ड मान से संबंधित भार शामिल हैं। इन वज़न और थ्रेसहोल्ड का मान किसी भी परिमित वास्तविक संख्या का हो सकता है।
थ्रेसहोल्ड गेट की मूल बातें
बता दें कि थ्रेसहोल्ड गेट के इनपुट X 1 , X 2 , X 3 ,…, X n हैं । इन निविष्टियों के संबंधित भार W 1 , W 2 , W 3 ,…, W n हैं । symbol थ्रेशोल्ड गेट को निम्न आकृति में दिखाया गया है।
Threshold gateको एक सर्कल के साथ दर्शाया गया है और इसमें 'n' इनपुट्स, X 1 से X n और सिंगल आउटपुट है। Y. इस सर्कल को दो भागों में बनाया गया है। एक भाग इनपुट के अनुरूप भार का प्रतिनिधित्व करता है और दूसरा भाग थ्रेसहोल्ड मान, T का प्रतिनिधित्व करता है।
इसी वज़न वाले इनपुट के उत्पादों का योग कहा जाता है weighted sum। यदि यह भारित राशि थ्रेशोल्ड मान से अधिक या बराबर है, तो केवल आउटपुट, Y एक के बराबर होगा। अन्यथा, आउटपुट, Y शून्य के बराबर होगा।
Mathematically, हम इस संबंध को थ्रेशोल्ड गेट के इनपुट और आउटपुट के बीच लिख सकते हैं।
$$Y=1, if \: \: W_{1}X_{1}+W_{2}X_{2}+W_{3}X_{3}+...W_{n}X_{n}\geq T$$
= 0, अन्यथा।
इसलिए, हम वज़न और / या थ्रेशोल्ड वैल्यू, टीटी के मूल्यों को बदलकर विभिन्न लॉजिक गेट्स और बुलियन फ़ंक्शंस लागू कर सकते हैं।
उदाहरण
हमें खोजने दो simplified Boolean function निम्नलिखित थ्रेसहोल्ड गेट के लिए।

इस थ्रेसहोल्ड गेट में तीन इनपुट X 1 , X 2 , X 3 और एक आउटपुट Y है।
आदानों एक्स 1 , एक्स 2 और एक्स 3 के वजन क्रमशः क्रमशः डब्ल्यू 1 = 2, डब्ल्यू 2 = 1 और डब्ल्यू 3 = -4 हैं।
थ्रेसहोल्ड गेट का मान T = -1 है।
weighted sum के थ्रेसहोल्ड गेट है
$$W=W_{1}X_{1}+W_{2}X_{2}+W_{3}X_{3}$$
ऊपर दिए गए समीकरण में दिए गए वज़न को प्रतिस्थापित करें।
$$\Rightarrow W=2X_{1}+X_{2}-4X_{3}$$
थ्रेसहोल्ड गेट का आउटपुट, Y 1 otherwise1 होने पर '1' होगा, अन्यथा यह '0' होगा।
निम्नलिखित table इनपुट के सभी संभावित संयोजन के लिए इनपुट और आउटपुट के बीच संबंध दिखाता है।
| इनपुट | भारी जोड | उत्पादन | ||
|---|---|---|---|---|
| $X_{1}$ | $X_{2}$ | $X_{3}$ | $W=2X_{1}+X_{2}-4X_{3}$ | $Y$ |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | -4 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | -3 | 0 |
| 1 | 0 | 0 | 2 | 1 |
| 1 | 0 | 1 | -2 | 0 |
| 1 | 1 | 0 | 3 | 1 |
| 1 | 1 | 1 | -1 | 1 |
उपरोक्त तालिका से, हम लिख सकते हैं Boolean function आउटपुट के लिए, वाई के रूप में
$$Y= \sum m\left ( 0,2,4,6,7 \right )$$
का उपयोग कर इस बूलियन समारोह का सरलीकरण 3 variable K-Map निम्नलिखित आकृति में दिखाया गया है।

इसलिए simplified Boolean function दिए गए थ्रेसहोल्ड गेट के लिए है $Y={X_{3}'}+X_{1}X_{2}$।
थ्रेसहोल्ड फ़ंक्शंस का संश्लेषण
थ्रेसहोल्ड गेट को भी कहा जाता है universal gateक्योंकि हम थ्रेसहोल्ड गेट (एस) का उपयोग करके किसी भी बूलियन फ़ंक्शन को लागू कर सकते हैं। कुछ-बार, एकल थ्रेसहोल्ड गेट का उपयोग करके कुछ लॉजिक गेट्स और बुलियन कार्यों को लागू करना संभव नहीं हो सकता है। उस स्थिति में, हमें कई थ्रेशोल्ड फाटकों की आवश्यकता हो सकती है।
इनका पालन करें steps एकल थ्रेसहोल्ड गेट का उपयोग करके बूलियन फ़ंक्शन को लागू करने के लिए।
Step 1 - फार्म a Truth table दिए गए बूलियन फ़ंक्शन के लिए।
Step 2 - उपरोक्त सत्य तालिका में, एक और कॉलम जोड़ें, जो बीच का संबंध बताता है weighted sums तथा Threshold value।
Step 3 - नीचे वर्णित के रूप में प्रत्येक संयोजन के लिए भारित रकम और सीमा के बीच संबंध लिखें।
यदि बूलियन फ़ंक्शन का आउटपुट 1 है, तो इनपुट के संयोजन के लिए भारित राशि थ्रेशोल्ड मान से अधिक या बराबर होगी।
यदि बूलियन फ़ंक्शन का आउटपुट 0 है, तो इनपुट के संयोजन के लिए भारित राशि थ्रेशोल्ड मान से कम होगी।
Step 4 - वज़न और थ्रेसहोल्ड के मूल्यों को इस तरह चुनें कि वे उपरोक्त तालिका के अंतिम कॉलम में मौजूद सभी संबंधों को संतुष्ट करें।
step 5 - ड्रा symbol उन भार और थ्रेशोल्ड मान के साथ थ्रेसहोल्ड गेट।
उदाहरण
आइए हम निम्नलिखित को लागू करें Boolean function एकल थ्रेसहोल्ड गेट का उपयोग करना।
$$Y\left ( X_{1},X_{2},X_{3} \right )=\sum m\left ( 0,2,4,6,7 \right )$$
दिया गया बूलियन फ़ंक्शन एक तीन चर फ़ंक्शन है, जिसे मिनिमम रूप में दर्शाया गया है। Truth table इस समारोह के नीचे दिखाया गया है।
| इनपुट | उत्पादन | ||
|---|---|---|---|
| X1 | X2 | X3 | Y |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
अब, उपरोक्त सत्य तालिका में एक और कॉलम जोड़ते हैं। इस अंतिम कॉलम में आपस में संबंध हैंweighted sums (W) and Threshold इनपुट के प्रत्येक संयोजन के लिए मूल्य (T)।
| इनपुट | उत्पादन | डब्ल्यू एंड टी के बीच संबंध | ||
|---|---|---|---|---|
| X1 | X2 | X3 | Y | |
| 0 | 0 | 0 | 1 | 0 ≥T |
| 0 | 0 | 1 | 0 | डब्ल्यू 3 <टी |
| 0 | 1 | 0 | 1 | डब्ल्यू 2 ≥ टी |
| 0 | 1 | 1 | 0 | डब्ल्यू 2 + डब्ल्यू 3 <टी |
| 1 | 0 | 0 | 1 | डब्ल्यू 1 ≥ टी |
| 1 | 0 | 1 | 0 | डब्ल्यू 1 + डब्ल्यू 3 <टी |
| 1 | 1 | 0 | 1 | डब्ल्यू 1 + डब्ल्यू 2। टी |
| 1 | 1 | 1 | 1 | डब्ल्यू 1 + डब्ल्यू 2 + डब्ल्यू 3। टी |
उपरोक्त तालिका से निष्कर्ष निम्नलिखित हैं।
थ्रेशोल्ड का मूल्य पहले संबंध के आधार पर या तो शून्य या नकारात्मक होना चाहिए।
डब्ल्यू 3 का मूल्य पहले और दूसरे संबंधों के आधार पर नकारात्मक होना चाहिए।
डब्ल्यू 1 और डब्ल्यू 2 के मूल्य पांचवें और तीसरे संबंधों के आधार पर थ्रेशोल्ड मान से अधिक या बराबर होना चाहिए।
डब्ल्यू 2 चौथे संबंध के आधार पर डब्ल्यू 3 से अधिक होना चाहिए ।
हम उपरोक्त निष्कर्षों के आधार पर वज़न और थ्रेसहोल्ड के लिए निम्न मान चुन सकते हैं।
डब्ल्यू 1 = 2, डब्ल्यू 2 = 1, डब्ल्यू 3 = -4 और टी = -1
symbol उपरोक्त मूल्यों के साथ थ्रेसहोल्ड गेट नीचे दिखाया गया है।

इसलिए, यह थ्रेसहोल्ड गेट दिए गए उपकरण को लागू करता है Boolean function, $Y\left ( X_{1}, X_{2},X_{3} \right )=\sum m\left ( 0,2,4,6,7 \right )$।
हमने पहले के अध्यायों में विभिन्न दहनशील सर्किटों पर चर्चा की। इन सभी सर्किट में आउटपुट (एस) का एक सेट होता है, जो केवल वर्तमान इनपुट के संयोजन पर निर्भर करता है। निम्नलिखित आंकड़ा दिखाता हैblock diagram अनुक्रमिक सर्किट की।
इस अनुक्रमिक सर्किट में इनपुट और आउटपुट (एस) का एक सेट होता है। अनुक्रमिक सर्किट का आउटपुट (एस) न केवल वर्तमान इनपुट के संयोजन पर निर्भर करता है, बल्कि पिछले आउटपुट (ओं) पर भी निर्भर करता है। पिछला उत्पादन और कुछ नहीं हैpresent state। इसलिए, अनुक्रमिक सर्किट में मेमोरी (भंडारण) तत्वों के साथ कॉम्बिनेशन सर्किट होते हैं। कुछ अनुक्रमिक सर्किटों में दहनशील सर्किट नहीं हो सकते हैं, लेकिन केवल स्मृति तत्व होते हैं।
निम्नलिखित तालिका शो differences संयोजन सर्किट और अनुक्रमिक सर्किट के बीच।
| संयुक्त सर्किट | अनुक्रमिक सर्किट |
|---|---|
| आउटपुट केवल वर्तमान इनपुट पर निर्भर करते हैं। | आउटपुट वर्तमान इनपुट और वर्तमान स्थिति दोनों पर निर्भर करते हैं। |
| प्रतिक्रिया पथ मौजूद नहीं है। | प्रतिक्रिया पथ मौजूद है। |
| मेमोरी तत्वों की आवश्यकता नहीं है। | मेमोरी तत्वों की आवश्यकता होती है। |
| घड़ी संकेत की आवश्यकता नहीं है। | घड़ी संकेत की आवश्यकता है। |
| डिजाइन करने में आसान। | डिजाइन करना मुश्किल। |
अनुक्रमिक सर्किट के प्रकार
निम्नलिखित दो प्रकार के अनुक्रमिक सर्किट हैं -
- अतुल्यकालिक अनुक्रमिक सर्किट
- सिंक्रोनस अनुक्रमिक सर्किट
अतुल्यकालिक अनुक्रमिक सर्किट
यदि अनुक्रमिक सर्किट के कुछ या सभी आउटपुट घड़ी संकेत के सक्रिय संक्रमण के संबंध में नहीं बदलते (प्रभावित) करते हैं, तो उस अनुक्रमिक सर्किट को कहा जाता है Asynchronous sequential circuit। इसका मतलब है, अतुल्यकालिक अनुक्रमिक सर्किट के सभी आउटपुट एक ही समय में (प्रभावित) नहीं बदलते हैं। इसलिए, अतुल्यकालिक अनुक्रमिक सर्किट के अधिकांश आउटपुट हैंnot in synchronous या तो केवल सकारात्मक किनारों या घड़ी संकेत के केवल नकारात्मक किनारों के साथ।
सिंक्रोनस अनुक्रमिक सर्किट
यदि घड़ी संकेत के सक्रिय संक्रमण के संबंध में एक अनुक्रमिक सर्किट परिवर्तन (प्रभावित) के सभी आउटपुट, तो उस अनुक्रमिक सर्किट को कहा जाता है Synchronous sequential circuit। इसका मतलब है, एक ही समय में सिंक्रोनस अनुक्रमिक सर्किट के सभी आउटपुट बदल जाते हैं (प्रभावित होते हैं)। इसलिए, तुल्यकालिक अनुक्रमिक सर्किट के आउटपुट या तो केवल सकारात्मक किनारों या घड़ी संकेत के केवल नकारात्मक किनारों के साथ समकालिक होते हैं।
घड़ी संकेत और ट्रिगर
इस खंड में, हम घड़ी संकेत और एक-एक करके ट्रिगर करने के प्रकारों के बारे में चर्चा करते हैं।
घड़ी का संकेत
क्लॉक सिग्नल एक आवधिक संकेत है और इसका ऑन टाइम और ऑफ टाइम समान नहीं होना चाहिए। हम एक के रूप में घड़ी संकेत का प्रतिनिधित्व कर सकते हैंsquare wave, जब इसका ऑन टाइम और ऑफ टाइम दोनों समान हो। यह घड़ी संकेत निम्न आकृति में दिखाया गया है।

n उपरोक्त आंकड़ा, वर्ग तरंग को घड़ी संकेत माना जाता है। यह संकेत कुछ समय के लिए लॉजिक हाई (5V) पर रहता है और बराबर समय के लिए लॉजिक लो (0V) पर रहता है। यह पैटर्न कुछ समय अवधि के साथ दोहराता है। इस मामले में,time period या तो दो बार के बराबर या दो बार के ऑफ टाइम के बराबर होगा।
हम घड़ी संकेत का प्रतिनिधित्व कर सकते हैं train of pulses, जब समय और बंद समय समान नहीं हैं। यह घड़ी संकेत निम्न आकृति में दिखाया गया है।

उपरोक्त आकृति में, दालों की ट्रेन को घड़ी संकेत माना जाता है। यह संकेत कुछ समय के लिए लॉजिक हाई (5V) पर रहता है और कुछ समय के लिए लॉजिक लो (0V) पर रहता है। यह पैटर्न कुछ समय अवधि के साथ दोहराता है। इस मामले में,time period समय और बंद समय के योग के बराबर होगा।
घड़ी संकेत की समय अवधि के पारस्परिक रूप से जाना जाता है frequencyघड़ी संकेत के। सभी अनुक्रमिक सर्किट घड़ी संकेत के साथ संचालित होते हैं। तो, आवृत्ति जिस पर अनुक्रमिक सर्किट संचालित किए जा सकते हैं, उसी के अनुसार घड़ी संकेत आवृत्ति को चुना जाना है।
ट्रिगरिंग के प्रकार
निम्नलिखित दो संभावित प्रकार हैं जो अनुक्रमिक सर्किट में उपयोग किए जाते हैं।
- स्तर ट्रिगरिंग
- बढ़त ट्रिगर
स्तर ट्रिगरिंग
दो स्तर हैं, लॉजिक उच्च और लॉजिक क्लॉक सिग्नल में कम। निम्नलिखित दो हैंtypes of level triggering।
- सकारात्मक स्तर ट्रिगर
- नकारात्मक स्तर ट्रिगर
यदि अनुक्रमिक सर्किट घड़ी सिग्नल के साथ संचालित होता है जब यह अंदर होता है Logic High, फिर उस प्रकार की ट्रिगरिंग के रूप में जाना जाता है Positive level triggering। इसे नीचे दिए गए आंकड़े में हाइलाइट किया गया है।
यदि अनुक्रमिक सर्किट घड़ी सिग्नल के साथ संचालित होता है जब यह अंदर होता है Logic Low, फिर उस प्रकार की ट्रिगरिंग के रूप में जाना जाता है Negative level triggering। इसे निम्न आकृति में हाइलाइट किया गया है।

बढ़त ट्रिगर
घड़ी संकेत में दो प्रकार के संक्रमण होते हैं। इसका मतलब है कि, क्लॉक सिग्नल ट्रांज़िशन या तो लॉजिक लॉजिक से लॉजिक हाई या लॉजिक हाई टू लॉजिक लो।
निम्नलिखित दो हैं types of edge triggering घड़ी संकेत के संक्रमण के आधार पर।
- सकारात्मक बढ़त ट्रिगर
- नकारात्मक बढ़त ट्रिगर
यदि अनुक्रमिक सर्किट को क्लॉक सिग्नल के साथ संचालित किया जाता है जो लॉजिक लो से लॉजिक हाई में परिवर्तित हो रहा है, तो उस प्रकार के ट्रिगर को किस रूप में जाना जाता है Positive edge triggering। इसे राइजिंग एज ट्रिगरिंग भी कहा जाता है। इसे निम्नलिखित आकृति में दिखाया गया है।

यदि अनुक्रमिक सर्किट को क्लॉक सिग्नल के साथ संचालित किया जाता है जो लॉजिक हाई से लॉजिक लो में परिवर्तित हो रहा है, तो उस प्रकार के ट्रिगरिंग के रूप में जाना जाता है Negative edge triggering। इसे गिरने वाला ट्रिगर भी कहा जाता है। इसे निम्नलिखित आकृति में दिखाया गया है।

आने वाले अध्यायों में, हम विभिन्न अनुक्रमिक सर्किटों के बारे में चर्चा करेंगे जो ट्रिगर के प्रकार पर आधारित हैं जो इसमें उपयोग किए जा सकते हैं।
ट्रिगरिंग के प्रकार के आधार पर दो प्रकार के मेमोरी तत्व हैं जो इसे संचालित करने के लिए उपयुक्त है।
- Latches
- Flip-flops
लैच सक्षम सिग्नल से संचालित होता है, जो है level sensitive। जबकि, फ्लिप-फ्लॉप एज सेंसिटिव हैं। हम अगले अध्याय में फ्लिप-फ्लॉप के बारे में चर्चा करेंगे। अब, एसआर लैच और डी लैच के बारे में एक-एक करके चर्चा करते हैं।
एसआर लाच
एसआर लाच को भी कहा जाता है Set Reset Latch। यह कुंडी तब तक आउटपुट को प्रभावित करती है जब तक कि सक्षम, E को '1' पर बनाए रखा जाता है। circuit diagram SR Latch को निम्न आकृति में दिखाया गया है।
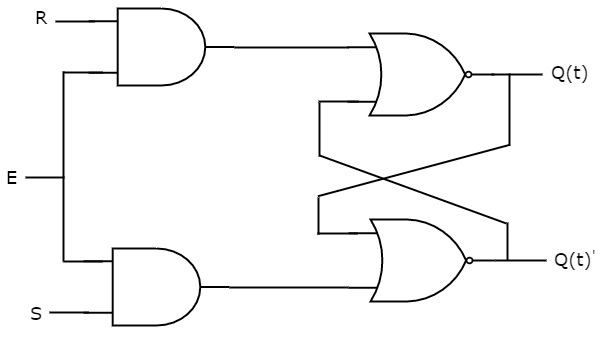
इस सर्किट में दो इनपुट एस एंड आर और दो आउटपुट क्यू (टी) और क्यू (टी) 'हैं। upper NOR gate वर्तमान स्थिति, क्यू (टी) के दो इनपुट आर एंड पूरक हैं और सक्षम होने पर, अगले राज्य, क्यू (टी + 1) का उत्पादन करता है, ई '1' है।
इसी तरह, lower NOR gate दो इनपुट एस एंड वर्तमान स्थिति, क्यू (टी) है और सक्षम होने पर अगले राज्य, क्यू (टी + 1) के पूरक का उत्पादन करता है, ई '1' है।
हम जानते हैं कि ए 2-input NOR gateएक आउटपुट उत्पन्न करता है, जो किसी अन्य इनपुट का पूरक होता है जब इनपुट में से एक '0' होता है। इसी तरह, यह '0' आउटपुट उत्पन्न करता है, जब इनपुट में से एक '1' होता है।
यदि S = 1 है, तो अगला राज्य Q (t + 1) वर्तमान स्थिति, Q (t) मानों के '1' के बराबर होगा।
यदि R = 1, तो अगला राज्य Q (t + 1) वर्तमान स्थिति, Q (t) मानों के '0' के बराबर होगा।
किसी भी समय, केवल उन दो इनपुट में '1' होना चाहिए। यदि दोनों इनपुट '1' हैं, तो अगला राज्य Q (t + 1) मान अपरिभाषित है।
निम्न तालिका से पता चलता है state table SR कुंडी की।
| रों | आर | क्यू (टी + 1) |
|---|---|---|
| 0 | 0 | क्यू (टी) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | - |
इसलिए, SR Latch इनपुट स्थितियों के आधार पर तीन प्रकार के कार्य करता है जैसे होल्ड, सेट और रीसेट।
D कुंडी
एसआर लैच की एक खामी है। जब दोनों इनपुट S & R एक हो तो अगले स्टेट वैल्यू की भविष्यवाणी नहीं की जा सकती है। तो, हम डी लैच द्वारा इस कठिनाई को दूर कर सकते हैं। इसे डाटा लैच भी कहा जाता है। circuit diagram D Latch को निम्न आकृति में दिखाया गया है।

इस सर्किट में एकल इनपुट डी और दो आउटपुट क्यू (टी) और क्यू (टी) 'है। D amp से S & amp; R इनपुट के बीच इन्वर्टर लगाकर SR Latch से D Latch प्राप्त किया जाता है और D को S से कनेक्ट किया जाता है। इसका मतलब है कि हमने S & R के संयोजन को समाप्त कर दिया है।
यदि D = 0 → S = 0 & R = 1 है, तो अगला राज्य Q (t + 1) वर्तमान स्थिति, Q (t) मानों के '0' के बराबर होगा। यह SR Latch राज्य तालिका की दूसरी पंक्ति के अनुरूप है।
यदि D = 1 → S = 1 & R = 0 है, तो अगला राज्य Q (t + 1) वर्तमान स्थिति, Q (t) मानों के '1' के बराबर होगा। यह SR Latch राज्य तालिका की तीसरी पंक्ति के समान है।
निम्न तालिका से पता चलता है state table D कुंडी की।
| घ | क्यू (टी + 1) |
|---|---|
| 0 | 0 |
| 1 | 1 |
इसलिए, D Latch डेटा इनपुट पर उपलब्ध जानकारी को पकड़कर रखें। D का मतलब है कि D Latch का आउटपुट इनपुट में परिवर्तन के प्रति संवेदनशील है, D जब तक सक्षम है उच्च है।
इस अध्याय में, हमने NOR फाटकों के बीच क्रॉस युग्मन प्रदान करके विभिन्न लाचेस को लागू किया। इसी तरह, आप NAND गेट्स का उपयोग करके इन Latches को लागू कर सकते हैं।
पिछले अध्याय में, हमने लाचेस के बारे में चर्चा की। वे फ्लिप-फ्लॉप के बुनियादी बिल्डिंग ब्लॉक हैं। हम दो तरीकों से फ्लिप-फ्लॉप को लागू कर सकते हैं।
पहली विधि में, cascade two latchesइस तरह से कि पहली कुंडी हर सकारात्मक घड़ी नाड़ी के लिए सक्षम है और दूसरी कुंडी हर नकारात्मक घड़ी नाड़ी के लिए सक्षम है। ताकि इन दो कुंडी का संयोजन एक फ्लिप-फ्लॉप बन जाए।
दूसरी विधि में, हम सीधे फ्लिप-फ्लॉप को लागू कर सकते हैं, जो कि किनारे संवेदनशील है। इस अध्याय में, हम निम्नलिखित पर चर्चा करते हैंflip-flops दूसरी विधि का उपयोग कर।
- एसआर फ्लिप-फ्लॉप
- डी फ्लिप-फ्लॉप
- जेके फ्लिप-फ्लॉप
- टी फ्लिप-फ्लॉप
एसआर फ्लिप-फ्लॉप
एसआर फ्लिप-फ्लॉप केवल सकारात्मक घड़ी संक्रमण या नकारात्मक घड़ी संक्रमण के साथ संचालित होता है। जबकि, SR लैच इनेबल सिग्नल से संचालित होता है। circuit diagram एसआर फ्लिप-फ्लॉप को निम्न आकृति में दिखाया गया है।

इस सर्किट में दो इनपुट एस एंड आर और दो आउटपुट क्यू (टी) और क्यू (टी) 'हैं। SR फ्लिपफ्लॉप का संचालन SR Latch के समान है। लेकिन, यह फ्लिप-फ्लॉप आउटपुट को तभी प्रभावित करता है जब सक्रिय सिग्नल के बजाय घड़ी सिग्नल के सकारात्मक संक्रमण को लागू किया जाता है।
निम्न तालिका से पता चलता है state table of SR फ्लिप-फ्लॉप
| रों | आर | क्यू (टी + 1) |
|---|---|---|
| 0 | 0 | क्यू (टी) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | - |
यहाँ, Q (t) और Q (t + 1) क्रमशः राज्य और अगला राज्य हैं। इसलिए, एसआर फ्लिप-फ्लॉप का उपयोग इन तीन कार्यों में से एक के लिए किया जा सकता है, जैसे कि होल्ड की स्थिति, इनपुट स्थितियों के आधार पर रीसेट और सेट जब घड़ी संकेत के सकारात्मक संक्रमण को लागू किया जाता है। निम्न तालिका से पता चलता हैcharacteristic table of SR फ्लिप-फ्लॉप
| प्रस्तुत इनपुट | वर्तमान स्थिति | अगला राज्य | |
|---|---|---|---|
| S | R | Q(t) | Q(t + 1) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | एक्स |
| 1 | 1 | 1 | एक्स |
तीन चर K-Map का उपयोग करके, हम अगले राज्य, Q (t + 1) के लिए सरलीकृत अभिव्यक्ति प्राप्त कर सकते हैं। three variable K-Map अगले राज्य के लिए, Q (t + 1) को निम्न आकृति में दिखाया गया है।

आसन्न लोगों के अधिकतम संभव समूह पहले से ही आंकड़े में दिखाए गए हैं। इसलिएsimplified expression अगले राज्य के लिए Q (t + 1) है
$Q\left ( t+1 \right )=S+{R}'Q\left ( t \right )$
डी फ्लिप-फ्लॉप
डी फ्लिप-फ्लॉप केवल सकारात्मक घड़ी संक्रमण या नकारात्मक घड़ी संक्रमण के साथ संचालित होता है। जबकि, डी लैच सक्षम सिग्नल से संचालित होता है। इसका मतलब है कि डी फ्लिप-फ्लॉप का आउटपुट क्लॉक सिग्नल के सक्रिय संक्रमण को छोड़कर, इनपुट में डी के प्रति असंवेदनशील है। circuit diagram of D फ्लिप-फ्लॉप को निम्न आकृति में दिखाया गया है।

इस सर्किट में एकल इनपुट डी और दो आउटपुट क्यू (टी) और क्यू (टी) 'है। डी फ्लिप-फ्लॉप का संचालन डी लैच के समान है। लेकिन, यह फ्लिप-फ्लॉप आउटपुट को तभी प्रभावित करता है जब सक्रिय सिग्नल के बजाय घड़ी सिग्नल के सकारात्मक संक्रमण को लागू किया जाता है।
निम्न तालिका से पता चलता है state table of D फ्लिप-फ्लॉप
| घ | Qt + 1t + 1 |
|---|---|
| 0 | 0 |
| 1 | 1 |
इसलिए, डी फ्लिप-फ्लॉप हमेशा सूचना को पकड़ो, जो डेटा इनपुट पर उपलब्ध है, डी सिग्नल ऑफ क्लॉक सिग्नल के पहले सकारात्मक संक्रमण। उपरोक्त राज्य तालिका से, हम अगले राज्य समीकरण को सीधे लिख सकते हैं
क्यू (टी + 1) = डी
डी फ्लिप-फ्लॉप की अगली स्थिति हमेशा डेटा इनपुट के बराबर होती है, घड़ी संकेत के हर सकारात्मक संक्रमण के लिए डी। इसलिए, डी फ्लिप-फ्लॉप का उपयोग रजिस्टरों में किया जा सकता है,shift registers और काउंटरों में से कुछ।
जेके फ्लिप-फ्लॉप
जेके फ्लिप-फ्लॉप एसआर फ्लिप-फ्लॉप का संशोधित संस्करण है। यह केवल सकारात्मक घड़ी संक्रमण या नकारात्मक घड़ी संक्रमण से संचालित होता है। circuit diagram जेके फ्लिप-फ्लॉप को निम्न आकृति में दिखाया गया है।
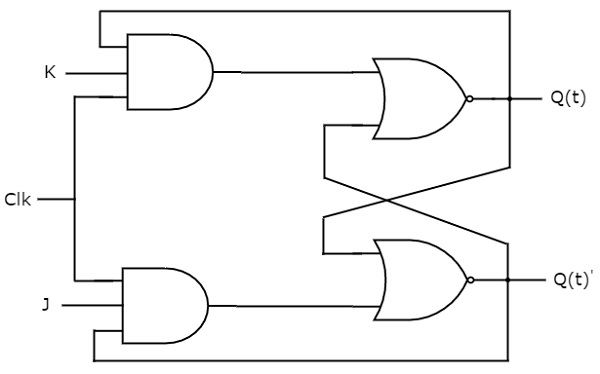
इस सर्किट में दो इनपुट जेएंडके और दो आउटपुट क्यू (टी) और क्यू (टी) 'हैं। जेके फ्लिप-फ्लॉप का संचालन एसआर फ्लिप-फ्लॉप के समान है। यहां, हमने SR फ्लिप-फ्लॉप के इनपुटों पर विचार कियाS = J Q(t)’ तथा R = KQ(t) इनपुट के 4 संयोजनों के लिए संशोधित SR फ्लिप-फ्लॉप का उपयोग करने के लिए।
निम्न तालिका से पता चलता है state table JK फ्लिप-फ्लॉप की।
| जे | क | क्यू (टी + 1) |
|---|---|---|
| 0 | 0 | क्यू (टी) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | क्यू (टी) ' |
यहाँ, Q (t) और Q (t + 1) क्रमशः राज्य और अगला राज्य हैं। तो, JK फ्लिप-फ्लॉप इन चार कार्यों में से एक के लिए इस्तेमाल किया जा सकता है, जैसे कि होल्ड की स्थिति, होल्ड, सेट और कॉम्प्लिमेंट, वर्तमान स्थिति के इनपुट स्थितियों के आधार पर, जब घड़ी संकेत का सकारात्मक संक्रमण लागू होता है। निम्न तालिका से पता चलता हैcharacteristic table JK फ्लिप-फ्लॉप की।
| प्रस्तुत इनपुट | वर्तमान स्थिति | अगला राज्य | |
|---|---|---|---|
| J | K | Q(t) | Q(t+1) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
तीन चर K-Map का उपयोग करके, हम अगले राज्य, Q (t + 1) के लिए सरलीकृत अभिव्यक्ति प्राप्त कर सकते हैं। Three variable K-Map अगले राज्य के लिए, Q (t + 1) को निम्न आकृति में दिखाया गया है।

आसन्न लोगों के अधिकतम संभव समूह पहले से ही आंकड़े में दिखाए गए हैं। इसलिएsimplified expression अगले राज्य के लिए Q (t + 1) है
$$Q\left ( t+1 \right )=J{Q\left ( t \right )}'+{K}'Q\left ( t \right )$$
टी फ्लिप-फ्लॉप
T फ्लिप-फ्लॉप JK फ्लिप-फ्लॉप का सरलीकृत संस्करण है। यह जेके फ्लिप-फ्लॉप के दोनों इनपुटों को एक ही इनपुट 'टी' से जोड़कर प्राप्त किया जाता है। यह केवल सकारात्मक घड़ी संक्रमण या नकारात्मक घड़ी संक्रमण से संचालित होता है। circuit diagram T फ्लिप-फ्लॉप को निम्न आकृति में दिखाया गया है।

इस सर्किट में एकल इनपुट टी और दो आउटपुट क्यू (टी) और क्यू (टी) 'है। टी फ्लिप-फ्लॉप का संचालन जेके फ्लिप-फ्लॉप के समान है। यहां, हमने जेके फ्लिप-फ्लॉप के इनपुटों पर विचार कियाJ = T तथा K = Tइनपुट के 2 संयोजनों के लिए संशोधित JK फ्लिप-फ्लॉप का उपयोग करने के लिए। इसलिए, हमने जम्मू और कश्मीर के अन्य दो संयोजनों को समाप्त कर दिया, जिसके लिए वे दो मूल्य टी फ्लिप-फ्लॉप में एक दूसरे के पूरक हैं।
निम्न तालिका से पता चलता है state table टी फ्लिप-फ्लॉप की।
| घ | क्यू (टी + 1) |
|---|---|
| 0 | क्यू (टी) |
| 1 | क्यू (टी) ' |
यहाँ, Q (t) और Q (t + 1) क्रमशः राज्य और अगला राज्य हैं। इसलिए, T फ्लिप-फ्लॉप का उपयोग इन दो कार्यों में से एक के लिए किया जा सकता है, जैसे होल्ड स्थिति, और इनपुट स्थितियों के आधार पर वर्तमान स्थिति का पूरक, जब घड़ी संकेत के सकारात्मक संक्रमण को लागू किया जाता है। निम्न तालिका से पता चलता हैcharacteristic table टी फ्लिप-फ्लॉप की।
| इनपुट | वर्तमान स्थिति | अगला राज्य |
|---|---|---|
| T | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
उपरोक्त विशेषता तालिका से, हम सीधे लिख सकते हैं next state equation जैसा
$$Q\left ( t+1 \right )={T}'Q\left ( t \right )+TQ{\left ( t \right )}'$$
$$\Rightarrow Q\left ( t+1 \right )=T\oplus Q\left ( t \right )$$
T फ्लिप-फ्लॉप का आउटपुट हमेशा घड़ी सिग्नल के हर सकारात्मक संक्रमण के लिए टॉगल करता है, जब इनपुट T लॉजिक हाई (1) पर रहता है। इसलिए, T फ्लिप-फ्लॉप का उपयोग किया जा सकता हैcounters।
इस अध्याय में, हमने NOR फाटकों के बीच क्रॉस युग्मन प्रदान करके विभिन्न फ्लिप-फ्लॉप को लागू किया। इसी तरह, आप NAND गेट्स का उपयोग करके इन फ्लिप-फ्लॉप को लागू कर सकते हैं।
पिछले अध्याय में, हमने चार फ्लिप-फ्लॉप, अर्थात् SR फ्लिप-फ्लॉप, डी फ्लिप-फ्लॉप, जेके फ्लिप-फ्लॉप और टी फ्लिप-फ्लॉप पर चर्चा की। हम कुछ अतिरिक्त तर्क को शामिल करके एक फ्लिप-फ्लॉप को शेष तीन फ्लिप-फ्लॉप में बदल सकते हैं। तो, कुल बारह होंगेflip-flop conversions।
इनका पालन करें steps एक फ्लिप-फ्लॉप को दूसरे में बदलने के लिए।
इसपर विचार करें characteristic table वांछित फ्लिप फ्लॉप की।
वर्तमान स्थिति और अगले राज्य के प्रत्येक संयोजन के लिए दिए गए फ्लिप-फ्लॉप के उत्तेजना मान (इनपुट) भरें। excitation table सभी फ्लिप-फ्लॉप के लिए नीचे दिखाया गया है।
| वर्तमान स्थिति | अगला राज्य | एसआर फ्लिप-फ्लॉप इनपुट | डी फ्लिप-फ्लॉप इनपुट | जेके फ्लिप-फ्लॉप इनपुट | टी फ्लिप-फ्लॉप इनपुट | ||
|---|---|---|---|---|---|---|---|
| Q(t) | Q(t+1) | S | R | D | J | K | T |
| 0 | 0 | 0 | एक्स | 0 | 0 | एक्स | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | एक्स | 1 |
| 1 | 0 | 0 | 1 | 0 | एक्स | 1 | 1 |
| 1 | 1 | एक्स | 0 | 1 | एक्स | 0 | 0 |
लाओ simplified expressionsप्रत्येक उत्तेजना इनपुट के लिए। यदि आवश्यक हो, सरलीकरण के लिए Kmaps का उपयोग करें।
खींचना circuit diagram वांछित फ्लिप-फ्लॉप और आवश्यक लॉजिक गेट्स का उपयोग करते हुए सरलीकृत अभिव्यक्तियों के अनुसार फ्लिप-फ्लॉप।
अब, हम कुछ फ्लिप-फ्लॉप को दूसरे में बदलते हैं। शेष फ्लिपफ्लॉप रूपांतरणों के लिए समान प्रक्रिया का पालन करें।
एसआर फ्लिप-फ्लॉप अन्य फ्लिप-फ्लॉप रूपांतरणों के लिए
एसआर फ्लिप-फ्लॉप के अन्य फ्लिप-फ्लॉप के तीन संभावित रूपांतरण निम्नलिखित हैं।
- एसआर फ्लिप-फ्लॉप से डी फ्लिप-फ्लॉप
- एसआर फ्लिप-फ्लॉप से जेके फ्लिप-फ्लॉप
- SR फ्लिप-फ्लॉप से T फ्लिप-फ्लॉप
एसआर फ्लिप-फ्लॉप से डी फ्लिप-फ्लॉप रूपांतरण
यहां, दिए गए फ्लिप-फ्लॉप SR फ्लिप-फ्लॉप हैं और वांछित फ्लिप-फ्लॉप D फ्लिप-फ्लॉप है। इसलिए, निम्नलिखित पर विचार करेंcharacteristic table of D फ्लिप-फ्लॉप
| डी फ्लिप-फ्लॉप इनपुट | वर्तमान स्थिति | अगला राज्य |
|---|---|---|
| D | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
हम जानते हैं कि एसआर फ्लिप-फ्लॉप में दो इनपुट एस एंड आर हैं। वर्तमान स्थिति और अगले राज्य मूल्यों के प्रत्येक संयोजन के लिए एसआर फ्लिप-फ्लॉप के उत्तेजना मूल्यों को लिखें। निम्न तालिका डी फ्लिप-फ्लॉप की विशेषता तालिका के साथ दिखाती हैexcitation inputs of SR फ्लिप-फ्लॉप
| डी फ्लिप-फ्लॉप इनपुट | वर्तमान स्थिति | अगला राज्य | एसआर फ्लिप-फ्लॉप इनपुट | |
|---|---|---|---|---|
| D | Q(t) | Q(t + 1) | S | R |
| 0 | 0 | 0 | 0 | एक्स |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | एक्स | 0 |
उपरोक्त तालिका से, हम लिख सकते हैं Boolean functions नीचे के रूप में प्रत्येक इनपुट के लिए।
$$S=m_{2}+d_{3}$$
$$R=m_{1}+d_{0}$$
हम इन आदानों के लिए सरलीकृत अभिव्यक्ति प्राप्त करने के लिए 2 चर K- मैप्स का उपयोग कर सकते हैं। k-Maps एस एंड आर के लिए नीचे दिखाया गया है।

इसलिए, सरलीकरण के बाद हमें S = D & R = D 'मिला। circuit diagram of D फ्लिप-फ्लॉप को निम्न आकृति में दिखाया गया है।

इस सर्किट में SR फ्लिप-फ्लॉप और एक इन्वर्टर शामिल हैं। यह इन्वर्टर एक आउटपुट का उत्पादन करता है, जो इनपुट का पूरक है। डी। तो, समग्र सर्किट में एकल इनपुट, डी और दो आउटपुट क्यू (टी) और क्यू (टी) है। इसलिए, यह एक हैD flip-flop। इसी तरह, आप अन्य दो रूपांतरण कर सकते हैं।
डी फ्लिप-फ्लॉप अन्य फ्लिप-फ्लॉप रूपांतरणों के लिए
डी फ्लिप-फ्लॉप के अन्य फ्लिप-फ्लॉप के तीन संभावित रूपांतरण निम्नलिखित हैं।
- D फ्लिप-फ्लॉप से T फ्लिप-फ्लॉप
- D फ्लिप-फ्लॉप से SR फ्लिप-फ्लॉप
- D फ्लिप-फ्लॉप से JK फ्लिप-फ्लॉप
D फ्लिप-फ्लॉप से T फ्लिप-फ्लॉप रूपांतरण
यहां, दिए गए फ्लिप-फ्लॉप डी फ्लिप-फ्लॉप हैं और वांछित फ्लिप-फ्लॉप टी फ्लिप-फ्लॉप है। इसलिए, निम्नलिखित पर विचार करेंcharacteristic table टी फ्लिप-फ्लॉप की।
| टी फ्लिप-फ्लॉप इनपुट | वर्तमान स्थिति | अगला राज्य |
|---|---|---|
| T | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
हम जानते हैं कि डी फ्लिप-फ्लॉप में एकल इनपुट डी है। इसलिए, वर्तमान राज्य और अगले राज्य मूल्यों के प्रत्येक संयोजन के लिए डी फ्लिप-फ्लॉप के उत्तेजना मूल्यों को लिखें। निम्न तालिका T फ्लिप-फ्लॉप की विशेषता तालिका के साथ दिखाता हैexcitation input of D फ्लिप-फ्लॉप
| टी फ्लिप-फ्लॉप इनपुट | वर्तमान स्थिति | अगला राज्य | डी फ्लिप-फ्लॉप इनपुट |
|---|---|---|---|
| T | Q(t) | Q(t + 1) | D |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
उपरोक्त तालिका से, हम सीधे लिख सकते हैं Boolean function नीचे के रूप में।
$$D=T\oplus Q\left ( t \right )$$
तो, हमें डी फ्लिप-फ्लॉप के साथ दो इनपुट एक्सक्लूसिव-ओआर गेट की आवश्यकता है। circuit diagram T फ्लिप-फ्लॉप को निम्न आकृति में दिखाया गया है।

इस सर्किट में डी फ्लिप-फ्लॉप और एक एक्सक्लूसिव-ओआर गेट होता है। यह एक्सक्लूसिव-ओआर गेट एक आउटपुट का उत्पादन करता है, जो एक्स-ओ ऑफ टी और क्यू (टी) है। तो, समग्र सर्किट में एकल इनपुट, टी और दो आउटपुट क्यू (टी) और क्यू (टी) 'है। इसलिए, यह एक हैT flip-flop। इसी तरह, आप अन्य दो रूपांतरण कर सकते हैं।
जेके फ्लिप-फ्लॉप अन्य फ्लिप-फ्लॉप रूपांतरणों के लिए
जेके फ्लिप-फ्लॉप के अन्य फ्लिप-फ्लॉप के तीन संभावित रूपांतरण निम्नलिखित हैं।
- JK फ्लिप-फ्लॉप से T फ्लिप-फ्लॉप
- JK फ्लिप-फ्लॉप से D फ्लिप-फ्लॉप
- जेके फ्लिप-फ्लॉप से एसआर फ्लिप-फ्लॉप
JK फ्लिप-फ्लॉप से T फ्लिप-फ्लॉप रूपांतरण
यहां, दिए गए फ्लिप-फ्लॉप JK फ्लिप-फ्लॉप हैं और वांछित फ्लिप-फ्लॉप T फ्लिप-फ्लॉप है। इसलिए, निम्नलिखित पर विचार करेंcharacteristic table टी फ्लिप-फ्लॉप की।
| टी फ्लिप-फ्लॉप इनपुट | वर्तमान स्थिति | अगला राज्य |
|---|---|---|
| T | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
हम जानते हैं कि जेके फ्लिप-फ्लॉप के दो इनपुट जेएंडके हैं, इसलिए वर्तमान राज्य और अगले राज्य मूल्यों के प्रत्येक संयोजन के लिए जेके फ्लिप-फ्लॉप के उत्तेजना मूल्यों को लिखें। निम्न तालिका T फ्लिप-फ्लॉप की विशेषता तालिका के साथ दिखाता हैexcitation inputs जेके फ्लिपफ्लॉप की।
| टी फ्लिप-फ्लॉप इनपुट | वर्तमान स्थिति | अगला राज्य | जेके फ्लिप-फ्लॉप इनपुट | |
|---|---|---|---|---|
| T | Q(t) | Q(t + 1) | J | K |
| 0 | 0 | 0 | 0 | एक्स |
| 0 | 1 | 1 | एक्स | 0 |
| 1 | 0 | 1 | 1 | एक्स |
| 1 | 1 | 0 | एक्स | 1 |
उपरोक्त तालिका से, हम लिख सकते हैं Boolean functions नीचे के रूप में प्रत्येक इनपुट के लिए।
$$J=m_{2}+d_{1}+d_{3}$$
$$K=m_{3}+d_{0}+d_{2}$$
हम इन दो इनपुट के लिए सरलीकृत अभिव्यक्ति प्राप्त करने के लिए 2 चर के-मैप का उपयोग कर सकते हैं। k-Maps जम्मू और कश्मीर के लिए नीचे दिखाए गए हैं।

तो, हमें सरलीकरण के बाद J = T & K = T मिला। circuit diagram T फ्लिप-फ्लॉप को निम्न आकृति में दिखाया गया है।

इस सर्किट में केवल JK फ्लिप-फ्लॉप है। इसके लिए किसी अन्य द्वार की आवश्यकता नहीं है। बस जम्मू और कश्मीर दोनों के लिए एक ही इनपुट टी को कनेक्ट करें। समग्र सर्किट में एकल इनपुट, टी और दो आउटपुट क्यू (टी) और क्यू (टी) हैं। इसलिए, यह एक हैT flip-flop। इसी तरह, आप अन्य दो रूपांतरण कर सकते हैं।
अन्य फ्लिप-फ्लॉप रूपांतरणों के लिए टी फ्लिप-फ्लॉप
टी फ्लिप-फ्लॉप के अन्य फ्लिप-फ्लॉप के तीन संभावित रूपांतरण निम्नलिखित हैं।
- T फ्लिप-फ्लॉप से D फ्लिप-फ्लॉप
- T फ्लिप-फ्लॉप से SR फ्लिप-फ्लॉप
- T फ्लिप-फ्लॉप से JK फ्लिप-फ्लॉप
T फ्लिप-फ्लॉप से D फ्लिप-फ्लॉप रूपांतरण
यहाँ, दिए गए फ्लिप-फ्लॉप T फ्लिप-फ्लॉप है और इच्छित फ्लिप-फ्लॉप D फ्लिप-फ्लॉप है। इसलिए, डी फ्लिप-फ्लॉप की विशेषता तालिका पर विचार करें और वर्तमान राज्य और अगले राज्य मूल्यों के प्रत्येक संयोजन के लिए टी फ्लिप-फ्लॉप के उत्तेजना मूल्यों को लिखें। निम्न तालिका से पता चलता हैcharacteristic table डी फ्लिप-फ्लॉप के साथ excitation input टी फ्लिप-फ्लॉप की।
| डी फ्लिप-फ्लॉप इनपुट | वर्तमान स्थिति | अगला राज्य | टी फ्लिप-फ्लॉप इनपुट | |
|---|---|---|---|---|
| D | Q(t) | Q(t + 1) | T | |
| 0 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 1 | |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 0 | |
उपरोक्त तालिका से, हम सीधे टी के बूलियन फ़ंक्शन को नीचे के रूप में लिख सकते हैं।
$$T=D\oplus Q\left ( t \right )$$
इसलिए, हमें T फ्लिप-फ्लॉप के साथ दो इनपुट एक्सक्लूसिव-ओआर गेट की आवश्यकता है। circuit diagram of D फ्लिप-फ्लॉप को निम्न आकृति में दिखाया गया है।

इस सर्किट में T फ्लिप-फ्लॉप और एक एक्सक्लूसिव-ओआर गेट है। यह एक्सक्लूसिव-ओआर गेट एक आउटपुट का उत्पादन करता है, जो एक्स-ओ ऑफ डी और क्यू (टी) है। तो, समग्र सर्किट में एकल इनपुट, डी और दो आउटपुट क्यू (टी) और क्यू (टी) 'है। इसलिए, यह एक हैD flip-flop। इसी तरह, आप अन्य दो रूपांतरण कर सकते हैं।
हम जानते हैं कि एक फ्लिप-फ्लॉप एक-बिट जानकारी संग्रहीत कर सकता है। जानकारी के कई बिट्स को स्टोर करने के लिए, हमें कई फ्लिप-फ्लॉप की आवश्यकता होती है। फ्लिप-फ्लॉप का समूह, जो बाइनरी डेटा को रखने (स्टोर) करने के लिए उपयोग किया जाता हैregister।
यदि रजिस्टर बिट्स को राइट हैंड साइड की ओर ले जाने में सक्षम है या लेफ्ट हैंड साइड की ओर जाना जाता है shift register। एक 'एन' बिट शिफ्ट रजिस्टर में 'एन' फ्लिप-फ्लॉप होता है। इनपुट्स लागू करने और आउटपुट एक्सेस करने के आधार पर चार प्रकार के शिफ्ट रजिस्टर निम्नलिखित हैं।
- सीरियल इन - सीरियल आउट शिफ्ट रजिस्टर
- सीरियल में - समानांतर आउट शिफ्ट रजिस्टर
- समानांतर इन - सीरियल आउट शिफ्ट रजिस्टर
- समानांतर इन - समानांतर आउट शिफ्ट रजिस्टर
सीरियल इन - सीरियल आउट (SISO) शिफ्ट रजिस्टर
शिफ्ट रजिस्टर, जो सीरियल इनपुट की अनुमति देता है और धारावाहिक आउटपुट का उत्पादन सीरियल-इन-सीरियल आउट के रूप में जाना जाता है (SISO)शिफ्ट का रजिस्टर। block diagram 3-बिट SISO शिफ्ट रजिस्टर निम्न आकृति में दिखाया गया है।

इस ब्लॉक आरेख में तीन डी फ्लिप-फ्लॉप होते हैं, जो हैं cascaded। इसका मतलब है, एक डी फ्लिप-फ्लॉप का आउटपुट अगले डी फ्लिप-फ्लॉप के इनपुट के रूप में जुड़ा हुआ है। ये सभी फ्लिप-फ्लॉप एक-दूसरे के साथ समकालिक हैं, एक ही घड़ी सिग्नल एक-दूसरे पर लागू होते हैं।
इस बदलाव रजिस्टर में, हम बाएं मोस्ट डी फ्लिप-फ्लॉप के इनपुट से बिट्स को क्रमिक रूप से भेज सकते हैं। इसलिए, इस इनपुट को भी कहा जाता हैserial input। क्लॉक सिग्नल की हर सकारात्मक बढ़त के लिए, डेटा एक चरण से दूसरे चरण में स्थानांतरित हो जाता है। तो, हम बिट्स को सबसे ज्यादा सही D फ्लिप-फ्लॉप के आउटपुट से प्राप्त कर सकते हैं। इसलिए, इस आउटपुट को भी कहा जाता हैserial output।
उदाहरण
हमें बाइनरी जानकारी भेजकर 3-बिट SISO शिफ्ट रजिस्टर के काम को देखते हैं “011” इनपुट पर LSB से MSB तक क्रमिक रूप से।
मान लें कि डी फ्लिप-फ्लॉप की प्रारंभिक स्थिति बाईं ओर से दाईं ओर है $Q_{2}Q_{1}Q_{0}=000$। हम समझ सकते हैंworking of 3-bit SISO shift register निम्न तालिका से।
| घड़ी की सकारात्मक बढ़त का नहीं | सीरियल इनपुट | क्यू २ | क्यू १ | प्रश्न ० |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 0 |
| 1 | 1 (LSB) | 1 | 0 | 0 |
| 2 | 1 | 1 | 1 | 0 |
| 3 | 0 (MSB) | 0 | 1 | 1 (LSB) |
| 4 | - | - | 0 | 1 |
| 5 | - | - | - | 0 (MSB) |
डी सिग्नल की अनुपस्थिति में डी फ्लिप-फ्लॉप की प्रारंभिक स्थिति है $Q_{2}Q_{1}Q_{0}=000$। यहां, सीरियल आउटपुट से आ रहा है$Q_{0}$। तो, एलएसबी (1) को घड़ी की 3 आरडी पॉजिटिव एज पर और एमएसबी (0) को क्लॉक के 5 वें पॉजिटिव एज पर प्राप्त किया जाता है ।
इसलिए, वैध आउटपुट का उत्पादन करने के लिए 3-बिट SISO शिफ्ट रजिस्टर को पांच घड़ी दालों की आवश्यकता होती है। इसी तरह,N-bit SISO shift register आवश्यक है 2N-1 'एन' बिट जानकारी को स्थानांतरित करने के लिए घड़ी की दाल।
सीरियल इन - पैरेलल आउट (SIPO) शिफ्ट रजिस्टर
शिफ्ट रजिस्टर, जो सीरियल इनपुट की अनुमति देता है और समानांतर आउटपुट पैदा करता है, सीरियल-इन-समानांतर आउट के रूप में जाना जाता है (SIPO)शिफ्ट का रजिस्टर। block diagram 3-बिट SIPO शिफ्ट रजिस्टर निम्न आकृति में दिखाया गया है।
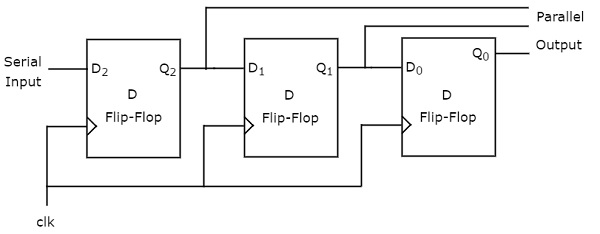
इस सर्किट में थ्री डी फ्लिप-फ्लॉप होते हैं, जिन्हें कैस्केड किया जाता है। इसका मतलब है, एक डी फ्लिप-फ्लॉप का आउटपुट अगले डी फ्लिप-फ्लॉप के इनपुट के रूप में जुड़ा हुआ है। ये सभी फ्लिप-फ्लॉप एक-दूसरे के साथ समकालिक हैं, एक ही घड़ी सिग्नल एक-दूसरे पर लागू होते हैं।
इस बदलाव रजिस्टर में, हम बाएं मोस्ट डी फ्लिप-फ्लॉप के इनपुट से बिट्स को क्रमिक रूप से भेज सकते हैं। इसलिए, इस इनपुट को भी कहा जाता हैserial input। क्लॉक सिग्नल की हर सकारात्मक बढ़त के लिए, डेटा एक चरण से दूसरे चरण में स्थानांतरित हो जाता है। इस मामले में, हम समानांतर में प्रत्येक डी फ्लिप-फ्लॉप के आउटपुट तक पहुंच सकते हैं। तो, हम प्राप्त करेंगेparallel outputs इस बदलाव रजिस्टर से।
उदाहरण
आइए हम बाइनरी जानकारी भेजकर 3-बिट SIPO शिफ्ट रजिस्टर का काम देखें “011” इनपुट पर LSB से MSB तक क्रमिक रूप से।
मान लें कि डी फ्लिप-फ्लॉप की प्रारंभिक स्थिति बाईं ओर से दाईं ओर है $Q_{2}Q_{1}Q_{0}=000$। यहाँ,$Q_{2}$ और $Q_{0}$क्रमशः MSB और LSB हैं। हम समझ सकते हैंworking of 3-bit SIPO shift register निम्न तालिका से।
| घड़ी की सकारात्मक बढ़त का नहीं | सीरियल इनपुट | क्यू 2 (MSB) | क्यू १ | क्यू 0 (एलएसबी) |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 0 |
| 1 | 1 (LSB) | 1 | 0 | 0 |
| 2 | 1 | 1 | 1 | 0 |
| 3 | 0 (MSB) | 0 | 1 | 1 |
डी सिग्नल की अनुपस्थिति में डी फ्लिप-फ्लॉप की प्रारंभिक स्थिति है $Q_{2}Q_{1}Q_{0}=000$। बाइनरी जानकारी“011” घड़ी के तीसरे सकारात्मक किनारे के लिए डी फ्लिप-फ्लॉप के आउटपुट पर समानांतर में प्राप्त किया जाता है।
इसलिए, वैध आउटपुट का उत्पादन करने के लिए 3-बिट SIPO शिफ्ट रजिस्टर में तीन घड़ी दालों की आवश्यकता होती है। इसी तरह,N-bit SIPO shift register requires N clock pulses in order to shift ‘N’ bit information.
Parallel In − Serial Out (PISO) Shift Register
The shift register, which allows parallel input and produces serial output is known as Parallel In − Serial Out (PISO) shift register. The block diagram of 3-bit PISO shift register is shown in the following figure.

This circuit consists of three D flip-flops, which are cascaded. That means, output of one D flip-flop is connected as the input of next D flip-flop. All these flip-flops are synchronous with each other since, the same clock signal is applied to each one.
In this shift register, we can apply the parallel inputs to each D flip-flop by making Preset Enable to 1. For every positive edge triggering of clock signal, the data shifts from one stage to the next. So, we will get the serial output from the right most D flip-flop.
Example
Let us see the working of 3-bit PISO shift register by applying the binary information “011” in parallel through preset inputs.
Since the preset inputs are applied before positive edge of Clock, the initial status of the D flip-flops from leftmost to rightmost will be $Q_{2}Q_{1}Q_{0}=011$. We can understand the working of 3-bit PISO shift register from the following table.
| No of positive edge of Clock | Q2 | Q1 | Q0 |
|---|---|---|---|
| 0 | 0 | 1 | 1(LSB) |
| 1 | - | 0 | 1 |
| 2 | - | - | 0(LSB) |
Here, the serial output is coming from $Q_{0}$. So, the LSB (1) is received before applying positive edge of clock and the MSB (0) is received at 2nd positive edge of clock.
Therefore, the 3-bit PISO shift register requires two clock pulses in order to produce the valid output. Similarly, the N-bit PISO shift register requires N-1 clock pulses in order to shift ‘N’ bit information.
Parallel In - Parallel Out (PIPO) Shift Register
The shift register, which allows parallel input and produces parallel output is known as Parallel In − Parallel Out (PIPO) shift register. The block diagram of 3-bit PIPO shift register is shown in the following figure.

This circuit consists of three D flip-flops, which are cascaded. That means, output of one D flip-flop is connected as the input of next D flip-flop. All these flip-flops are synchronous with each other since, the same clock signal is applied to each one.
In this shift register, we can apply the parallel inputs to each D flip-flop by making Preset Enable to 1. We can apply the parallel inputs through preset or clear. These two are asynchronous inputs. That means, the flip-flops produce the corresponding outputs, based on the values of asynchronous inputs. In this case, the effect of outputs is independent of clock transition. So, we will get the parallel outputs from each D flip-flop.
उदाहरण
आइए हम बाइनरी जानकारी को लागू करके 3-बिट PIPO शिफ्ट रजिस्टर का काम देखते हैं “011” प्रीसेट इनपुट के माध्यम से समानांतर में।
चूँकि पूर्व निर्धारित निविष्टियाँ घड़ी के सकारात्मक किनारे से पहले लागू की जाती हैं, डी की प्रारंभिक स्थिति बाईं ओर से दाईं ओर फ़्लॉप होती है $Q_{2}Q_{1}Q_{0}=011$। तो, बाइनरी जानकारी“011” घड़ी के सकारात्मक किनारे लगाने से पहले डी फ्लिप-फ्लॉप के आउटपुट पर समानांतर में प्राप्त किया जाता है।
इसलिए, वैध आउटपुट का उत्पादन करने के लिए 3-बिट PIPO शिफ्ट रजिस्टर को शून्य घड़ी दालों की आवश्यकता होती है। इसी तरह,N-bit PIPO shift register 'एन' बिट जानकारी को स्थानांतरित करने के लिए किसी भी घड़ी की नब्ज की आवश्यकता नहीं होती है।
पिछले अध्याय में, हमने चार प्रकार के शिफ्ट रजिस्टर की चर्चा की। आवश्यकता के आधार पर, हम उन शिफ्ट रजिस्टरों में से एक का उपयोग कर सकते हैं। शिफ्ट रजिस्टर के आवेदन निम्नलिखित हैं।
पाली रजिस्टर के रूप में प्रयोग किया जाता है Parallel to serial converter, जो समानांतर डेटा को सीरियल डेटा में परिवर्तित करता है। इसका उपयोग एनालॉग से डिजिटल कन्वर्टर (ADC) ब्लॉक के बाद ट्रांसमीटर सेक्शन में किया जाता है।
पाली रजिस्टर के रूप में प्रयोग किया जाता है Serial to parallel converter, जो सीरियल डेटा को समानांतर डेटा में परिवर्तित करता है। इसका उपयोग डिजिटल से एनालॉग कनवर्टर (डीएसी) ब्लॉक से पहले रिसीवर सेक्शन में किया जाता है।
कुछ अतिरिक्त गेटों के साथ शिफ्ट रजिस्टर शून्य और लोगों के अनुक्रम को उत्पन्न करता है। इसलिए, इसका उपयोग किया जाता हैsequence generator।
शिफ्ट रजिस्टर का भी उपयोग किया जाता है counters। दाएं से दो प्रकार के काउंटर हैं जो आउटपुट के प्रकार पर आधारित हैं, अधिकांश डी फ्लिप-फ्लॉप सीरियल इनपुट से जुड़ा हुआ है। वे रिंग काउंटर और जॉनसन रिंग काउंटर हैं।
इस अध्याय में, आइए एक-एक करके इन दो काउंटरों के बारे में चर्चा करें।
रिंग काउंटर
पिछले अध्याय में, हमने सीरियल इन - पैरेलल आउट के संचालन पर चर्चा की (SIPO)शिफ्ट का रजिस्टर। यह धारावाहिक रूप में बाहर से डेटा स्वीकार करता है और इसे 'एन' बिट डेटा को शिफ्ट करने के लिए 'एन' क्लॉक दाल की आवश्यकता होती है।
इसी तरह, ‘N’ bit Ring counterसमान ऑपरेशन करता है। लेकिन, फर्क सिर्फ इतना है कि सबसे दाएं फ्लिप-फ्लॉप का आउटपुट बाहर से डेटा अप्लाई करने के बजाय लेफ्ट डी फ्लिप-फ्लॉप के इनपुट के रूप में दिया जाता है। इसलिए, रिंग काउंटर राज्यों के एक क्रम (शून्य और लोगों का पैटर्न) का उत्पादन करता है और यह प्रत्येक के लिए दोहराता है‘N’ clock cycles।
block diagram 3-बिट रिंग काउंटर को निम्न आकृति में दिखाया गया है।
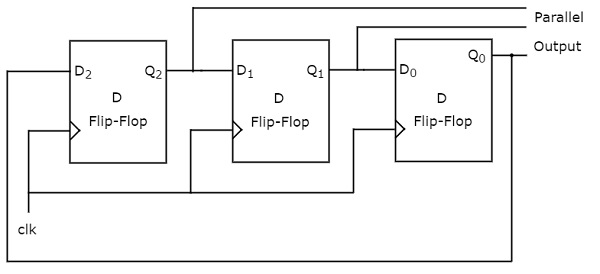
3-बिट रिंग काउंटर में केवल 3-बिट SIPO शिफ्ट रजिस्टर होता है। सबसे दाहिने D फ्लिप-फ्लॉप का आउटपुट बाएं सबसे D फ्लिप-फ्लॉप के सीरियल इनपुट से जुड़ा है।
मान लें कि डी फ्लिप-फ्लॉप की प्रारंभिक स्थिति बाईं ओर से दाईं ओर है $Q_{2}Q_{1}Q_{0}=001$। यहाँ,$Q_{2}$ और $Q_{0}$क्रमशः MSB और LSB हैं। हम समझ सकते हैंworking of Ring counter निम्न तालिका से।
| घड़ी की सकारात्मक बढ़त का नहीं | सीरियल इनपुट = क्यू ० | क्यू 2 (MSB) | क्यू १ | क्यू 0 (एलएसबी) |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 1 |
डी सिग्नल की अनुपस्थिति में डी फ्लिप-फ्लॉप की प्रारंभिक स्थिति है $Q_{2}Q_{1}Q_{0}=001$। यह स्थिति घड़ी संकेत के हर तीन सकारात्मक बढ़त संक्रमणों के लिए दोहराती है।
इसलिए, निम्नलिखित operations घड़ी संकेत के हर सकारात्मक बढ़त के लिए जगह ले लो।
पहले D फ्लिप-फ्लॉप के सीरियल इनपुट को तीसरे फ्लिप-फ्लॉप का पिछला आउटपुट मिलता है। तो, पहले D फ्लिप-फ्लॉप का वर्तमान आउटपुट तीसरे फ्लिप-फ्लॉप के पिछले आउटपुट के बराबर है।
पहले और दूसरे डी फ्लिप-फ्लॉप के पिछले आउटपुट एक बिट से सही स्थानांतरित हो जाते हैं। इसका मतलब है कि, दूसरे और तीसरे डी फ्लिप-फ्लॉप के वर्तमान आउटपुट पहले और दूसरे डी फ्लिप-फ्लॉप के पिछले आउटपुट के बराबर हैं।
जॉनसन रिंग काउंटर
का संचालन Johnson Ring counterयह रिंग काउंटर के समान है। लेकिन, एकमात्र अंतर यह है कि सबसे सामान्य डी फ्लिप-फ्लॉप के पूरक आउटपुट को सामान्य आउटपुट के बजाय लेफ्ट डी डी फ्लिप-फ्लॉप के इनपुट के रूप में दिया जाता है। इसलिए, 'एन' बिट जॉनसन रिंग काउंटर राज्यों के एक क्रम (शून्य और लोगों का पैटर्न) का उत्पादन करता है और यह प्रत्येक के लिए दोहराता है‘2N’ clock cycles।
जॉनसन रिंग काउंटर भी कहा जाता है Twisted Ring counterऔर स्विच पूंछ अंगूठी काउंटर। block diagram 3-बिट जॉनसन रिंग काउंटर को निम्न आकृति में दिखाया गया है।

3-बिट जॉनसन रिंग काउंटर में केवल 3-बिट SIPO शिफ्ट रजिस्टर होता है। दाएं फ्लिप फ्लिप फ्लॉप का पूरक आउटपुट लेफ्ट मोस्ट डी फ्लिप-फ्लॉप के सीरियल इनपुट से जुड़ा है।
मान लें, शुरू में सभी डी फ्लिप-फ्लॉप साफ हो गए हैं। इसलिए,$Q_{2}Q_{1}Q_{0}=000$। यहाँ,$Q_{2}$ और $Q_{0}$क्रमशः MSB और LSB हैं। हम समझ सकते हैंworking निम्नलिखित तालिका से जॉनसन रिंग काउंटर की।
| घड़ी की सकारात्मक बढ़त का नहीं | सीरियल इनपुट = क्यू ० | क्यू 2 (MSB) | क्यू १ | क्यू 0 (एलएसबी) |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 2 | 1 | 1 | 1 | 0 |
| 3 | 1 | 1 | 1 | 1 |
| 4 | 0 | 0 | 1 | 1 |
| 5 | 0 | 0 | 0 | 1 |
| 6 | 0 | 0 | 0 | 0 |
डी सिग्नल की अनुपस्थिति में डी फ्लिप-फ्लॉप की प्रारंभिक स्थिति है $Q_{2}Q_{1}Q_{0}=000$। यह स्थिति घड़ी संकेत के प्रत्येक छह सकारात्मक बढ़त संक्रमणों के लिए दोहराती है।
इसलिए, निम्नलिखित operations घड़ी संकेत के हर सकारात्मक बढ़त के लिए जगह ले लो।
पहले D फ्लिप-फ्लॉप के सीरियल इनपुट को तीसरे फ्लिप-फ्लॉप के पिछले पूरक आउटपुट मिलते हैं। तो, पहले D फ्लिप-फ्लॉप का वर्तमान आउटपुट तीसरे फ्लिप-फ्लॉप के पिछले पूरक आउटपुट के बराबर है।
पहले और दूसरे डी फ्लिप-फ्लॉप के पिछले आउटपुट एक बिट से सही स्थानांतरित हो जाते हैं। इसका मतलब है कि, दूसरे और तीसरे डी फ्लिप-फ्लॉप के वर्तमान आउटपुट पहले और दूसरे डी फ्लिप-फ्लॉप के पिछले आउटपुट के बराबर हैं।
पिछले दो अध्यायों में, हमने विभिन्न बदलाव रजिस्टर और चर्चा की counters using D flipflops। अब, हम टी फ्लिप-फ्लॉप का उपयोग करते हुए विभिन्न काउंटरों पर चर्चा करते हैं। हम जानते हैं कि टी फ्लिप-फ्लॉप घड़ी संकेत के हर सकारात्मक छोर के लिए या घड़ी संकेत के नकारात्मक किनारे के लिए आउटपुट को जन्म देता है।
एक 'एन' बिट बाइनरी काउंटर में 'एन' टी फ्लिप-फ्लॉप होते हैं। यदि काउंटर 0 से 2 तक गिना जाता है - 1, तब इसे बाइनरी कहा जाता है up counter। इसी तरह, यदि काउंटर 2 से नीचे गिना जाता है - 1 से 0, तब इसे बाइनरी कहा जाता है down counter।
वहाँ दॊ है types of counters फ्लिप-फ्लॉप के आधार पर जो तुल्यकालिक या नहीं में जुड़े हुए हैं।
- अतुल्यकालिक काउंटर
- तुल्यकालिक काउंटर
अतुल्यकालिक काउंटर
यदि फ्लिप-फ्लॉप को एक ही घड़ी संकेत नहीं मिलता है, तो उस काउंटर को कहा जाता है Asynchronous counter। सिस्टम क्लॉक का आउटपुट क्लॉक सिग्नल के रूप में केवल पहले फ्लिप-फ्लॉप पर लागू होता है। शेष फ्लिप-फ्लॉप अपने पिछले चरण फ्लिप-फ्लॉप के आउटपुट से घड़ी संकेत प्राप्त करते हैं। इसलिए, सभी फ्लिप-फ्लॉप के आउटपुट एक ही समय में (प्रभावित) नहीं बदलते हैं।
अब, हम एक-एक करके निम्नलिखित दो काउंटरों पर चर्चा करते हैं।
- अतुल्यकालिक बाइनरी अप काउंटर
- अतुल्यकालिक बाइनरी डाउन काउंटर
अतुल्यकालिक बाइनरी अप काउंटर
एक 'एन' बिट एसिंक्रोनस बाइनरी अप काउंटर में 'एन' टी फ्लिप-फ्लॉप होते हैं। यह 0 से 2 तक गिना जाता है - 1. block diagram 3-बिट अतुल्यकालिक बाइनरी अप काउंटर को निम्न आकृति में दिखाया गया है।

3-बिट एसिंक्रोनस बाइनरी अप काउंटर में तीन टी फ्लिप-फ्लॉप होते हैं और सभी फ्लिप-फ्लॉप के टी-इनपुट '1' से जुड़े होते हैं। ये सभी फ्लिप-फ्लॉप नकारात्मक बढ़त के कारण हैं लेकिन आउटपुट असिंक्रोनस रूप से बदलते हैं। घड़ी संकेत सीधे पहले टी फ्लिप-फ्लॉप पर लागू होता है। तो, पहले टी फ्लिप-फ्लॉप का आउटपुटtoggles घड़ी संकेत के हर नकारात्मक किनारे के लिए।
पहले T फ्लिप-फ्लॉप का आउटपुट दूसरे T फ्लिप-फ्लॉप के लिए क्लॉक सिग्नल के रूप में लागू होता है। तो, पहले टी फ्लिप-फ्लॉप के उत्पादन के हर नकारात्मक किनारे के लिए दूसरा टी फ्लिप-फ्लॉप टॉगल का उत्पादन। इसी तरह, दूसरे टी फ्लिप-फ्लॉप के उत्पादन के हर नकारात्मक किनारे के लिए तीसरे टी फ्लिप-फ्लॉप टॉगल का उत्पादन होता है, क्योंकि दूसरा टी फ्लिप-फ्लॉप का आउटपुट तीसरे टी फ्लिप-फ्लॉप के लिए घड़ी संकेत के रूप में कार्य करता है।
टी फ्लिप-फ्लॉप की प्रारंभिक स्थिति को दाईं से बाईं ओर मान लें $Q_{2}Q_{1}Q_{0}=000$। यहाँ,$Q_{2}$ और $Q_{0}$क्रमशः MSB और LSB हैं। हम समझ सकते हैंworking निम्न तालिका से 3-बिट अतुल्यकालिक बाइनरी काउंटर।
| घड़ी की कोई नकारात्मक धार नहीं | क्यू 0 (एलएसबी) | क्यू १ | क्यू 2 (MSB) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 1 | 1 | 0 |
| 4 | 0 | 0 | 1 |
| 5 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 |
| 7 | 1 | 1 | 1 |
यहाँ $Q_{0}$ घड़ी संकेत के हर नकारात्मक किनारे के लिए टॉगल किया गया। $Q_{1}$ हर के लिए भीख मांगी $Q_{0}$यह 1 से 0 तक चला जाता है, अन्यथा पिछली स्थिति में रहता है। इसी तरह,$Q_{2}$ हर के लिए भीख मांगी $Q_{1}$ यह 1 से 0 तक चला जाता है, अन्यथा पिछली स्थिति में रहता है।
घड़ी संकेत की अनुपस्थिति में टी फ्लिप-फ्लॉप की प्रारंभिक स्थिति है $Q_{2}Q_{1}Q_{0}=000$। यह घड़ी संकेत के प्रत्येक नकारात्मक किनारे के लिए एक से बढ़ कर है और घड़ी संकेत के 7 वें नकारात्मक किनारे पर अधिकतम मूल्य तक पहुंच गया है । जब घड़ी संकेत के नकारात्मक किनारों को लागू किया जाता है तो यह पैटर्न दोहराता है।
अतुल्यकालिक बाइनरी डाउन काउंटर
एक 'एन' बिट असिंक्रोनस बाइनरी डाउन काउंटर में 'एन' टी फ्लिप-फ्लॉप होते हैं। यह 2 से मायने रखता है - 1 से 0. block diagram 3-बिट अतुल्यकालिक बाइनरी डाउन काउंटर निम्न आकृति में दिखाया गया है।

3-बिट एसिंक्रोनस बाइनरी डाउन काउंटर का ब्लॉक आरेख 3-बिट एसिंक्रोनस बाइनरी काउंटर के ब्लॉक आरेख के समान है। लेकिन, एकमात्र अंतर यह है कि एक चरण के फ्लिप-फ्लॉप के सामान्य आउटपुट को कनेक्ट करने के बजाय अगले चरण के लिए घड़ी संकेत के रूप में फ्लिप-फ्लॉप, कनेक्ट करेंcomplemented outputsअगले चरण फ्लिप-फ्लॉप के लिए घड़ी संकेत के रूप में एक चरण फ्लिप-फ्लॉप। पूरक उत्पादन 1 से 0 तक जाता है, सामान्य उत्पादन 0 से 1 तक जाता है।
टी फ्लिप-फ्लॉप की प्रारंभिक स्थिति को दाईं से बाईं ओर मान लें $Q_{2}Q_{1}Q_{0}=000$। यहाँ,$Q_{2}$ और $Q_{0}$क्रमशः MSB और LSB हैं। हम समझ सकते हैंworking निम्न तालिका से 3-बिट अतुल्यकालिक बाइनरी डाउन काउंटर।
| घड़ी की कोई नकारात्मक धार नहीं | क्यू 0 (एलएसबी) | क्यू १ | क्यू 2 (MSB) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 0 | 1 | 1 |
| 3 | 1 | 0 | 1 |
| 4 | 0 | 0 | 1 |
| 5 | 1 | 1 | 0 |
| 6 | 0 | 1 | 0 |
| 7 | 1 | 0 | 0 |
यहाँ $Q_{0}$ घड़ी संकेत के हर नकारात्मक किनारे के लिए टॉगल किया गया। $Q_{1}$ हर के लिए भीख मांगी $Q_{0}$यह 0 से 1 तक जाता है, अन्यथा पिछले स्थिति में बना रहा। इसी तरह,$Q_{2}$ हर के लिए भीख मांगी $Q_{1}$ यह 0 से 1 तक जाता है, अन्यथा पिछले स्थिति में बना रहा।
घड़ी संकेत की अनुपस्थिति में टी फ्लिप-फ्लॉप की प्रारंभिक स्थिति है $Q_{2}Q_{1}Q_{0}=000$। यह घड़ी के संकेत के प्रत्येक नकारात्मक किनारे के लिए एक से घटाया जाता है और घड़ी के संकेत के 8 वें नकारात्मक किनारे पर समान मूल्य तक पहुंचता है । जब घड़ी संकेत के नकारात्मक किनारों को लागू किया जाता है तो यह पैटर्न दोहराता है।
तुल्यकालिक काउंटर
यदि सभी फ्लिप-फ्लॉप समान घड़ी संकेत प्राप्त करते हैं, तो उस काउंटर को कहा जाता है Synchronous counter। इसलिए, सभी फ्लिप-फ्लॉप के आउटपुट एक ही समय में बदलते (प्रभावित) होते हैं।
अब, हम एक-एक करके निम्नलिखित दो काउंटरों पर चर्चा करते हैं।
- सिंक्रोनस बाइनरी अप काउंटर
- सिंक्रोनस बाइनरी डाउन काउंटर
सिंक्रोनस बाइनरी अप काउंटर
एक 'एन' बिट सिंक्रोनस बाइनरी अप काउंटर में 'एन' टी फ्लिप-फ्लॉप होते हैं। यह 0 से 2 तक गिना जाता है - 1. block diagram 3-बिट सिंक्रोनस बाइनरी अप काउंटर को निम्न आकृति में दिखाया गया है।

3-बिट सिंक्रोनस बाइनरी अप काउंटर में तीन टी फ्लिप-फ्लॉप और एक 2-इनपुट और गेट शामिल हैं। ये सभी फ्लिप-फ्लॉप नकारात्मक बढ़त के कारण होते हैं और फ्लिप-फ्लॉप के आउटपुट तुल्यकालिक रूप से बदल जाते हैं (प्रभावित होते हैं)। पहले, दूसरे और तीसरे फ्लिप-फ्लॉप के टी इनपुट 1 हैं,$Q_{0}$ और $Q_{1}Q_{0}$ क्रमशः।
पहले टी फ्लिप-फ्लॉप का आउटपुट togglesघड़ी संकेत के हर नकारात्मक किनारे के लिए। अगर घड़ी संकेत के हर नकारात्मक किनारे के लिए दूसरा टी फ्लिप-फ्लॉप टॉगल का उत्पादन$Q_{0}$ है 1. क्लॉक सिग्नल के प्रत्येक नकारात्मक किनारे के लिए तीसरे टी फ्लिप-फ्लॉप टॉगल का आउटपुट यदि दोनों $Q_{0}$ और $Q_{1}$ 1 हैं।
सिंक्रोनस बाइनरी डाउन काउंटर
एक 'एन' बिट सिंक्रोनस बाइनरी डाउन काउंटर में 'एन' टी फ्लिप-फ्लॉप होते हैं। यह 2 से मायने रखता है - 1 से 0. block diagram 3-बिट सिंक्रोनस बाइनरी डाउन काउंटर को निम्न आकृति में दिखाया गया है।

3-बिट सिंक्रोनस बाइनरी डाउन काउंटर में तीन टी फ्लिप-फ्लॉप और एक 2-इनपुट और गेट शामिल हैं। ये सभी फ्लिप-फ्लॉप नकारात्मक बढ़त के कारण होते हैं और फ्लिप-फ्लॉप के आउटपुट तुल्यकालिक रूप से बदल जाते हैं (प्रभावित होते हैं)। पहले, दूसरे और तीसरे फ्लिप-फ्लॉप के टी इनपुट 1 हैं,${Q_{0}}'$ और ' ${Q_{1}}'$${Q_ {0}} क्रमशः $।
पहले टी फ्लिप-फ्लॉप का आउटपुट togglesघड़ी संकेत के हर नकारात्मक किनारे के लिए। अगर $ {Q_ {0}} 'घड़ी संकेत के हर नकारात्मक किनारे के लिए दूसरा टी फ्लिप-फ्लॉप टॉगल का आउटपुट'$ is 1. The output of third T flip-flop toggles for every negative edge of clock signal if both ${Q_ {1}} '$ & ${Q_ {0}} '$ 1 हैं।
हम जानते हैं कि समकालिक अनुक्रमिक सर्किट इनपुट के आधार पर घड़ी संकेत के हर सकारात्मक (या नकारात्मक) संक्रमण के लिए अपने राज्यों को बदलते (प्रभावित) करते हैं। तो, तुल्यकालिक अनुक्रमिक सर्किट के इस व्यवहार को चित्रमय रूप में दर्शाया जा सकता है और इसे इस रूप में जाना जाता हैstate diagram।
एक तुल्यकालिक अनुक्रमिक सर्किट भी कहा जाता है Finite State Machine(एफएसएम), यदि इसके पास राज्यों की सीमित संख्या है। FSM दो प्रकार के होते हैं।
- मैली स्टेट मशीन
- मूर स्टेट मशीन
अब, हम एक-एक करके इन दो राज्य मशीनों के बारे में चर्चा करते हैं।
मैली स्टेट मशीन
एक परिमित राज्य मशीन को मेईली स्टेट मशीन कहा जाता है, यदि आउटपुट वर्तमान इनपुट और वर्तमान स्थिति दोनों पर निर्भर करते हैं। block diagram Mealy स्टेट मशीन को निम्न आकृति में दिखाया गया है।
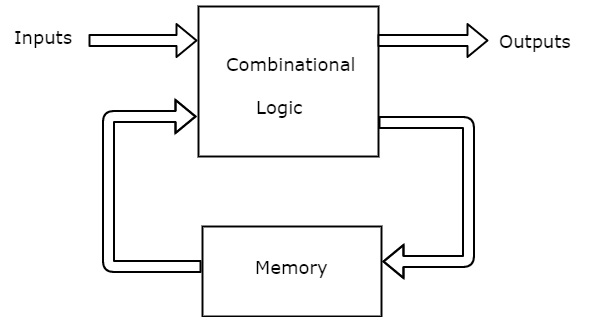
जैसा कि चित्र में दिखाया गया है, मेयली स्टेट मशीन में दो भाग मौजूद हैं। वे जुझारू तर्क और स्मृति हैं। मेमोरी पिछले आउटपुट के कुछ या कुछ भाग प्रदान करने के लिए उपयोगी है(present states) संयोजन तर्क के इनपुट के रूप में।
इसलिए, वर्तमान इनपुट और वर्तमान स्थिति के आधार पर, मेयली स्टेट मशीन आउटपुट उत्पन्न करती है। इसलिए, आउटपुट केवल घड़ी संकेत के सकारात्मक (या नकारात्मक) संक्रमण पर मान्य होंगे।
state diagram Mealy स्टेट मशीन को निम्न आकृति में दिखाया गया है।
उपरोक्त आंकड़ों में, तीन राज्य हैं, ए, बी और सी। इन राज्यों को मंडलियों के अंदर लेबल किया गया है और प्रत्येक सर्कल एक राज्य से मेल खाती है। इन राज्यों के बीच के बदलावों को निर्देशित लाइनों के साथ दर्शाया गया है। यहाँ, 0/0, 1/0 और 1/1 निरूपित करता हैinput / output। उपरोक्त आंकड़ों में, इनपुट के मान के आधार पर प्रत्येक राज्य से दो संक्रमण होते हैं, x।
सामान्य तौर पर, म्याऊ राज्य मशीन में आवश्यक राज्यों की संख्या मूर राज्य मशीन में आवश्यक राज्यों की संख्या से कम या बराबर होती है। प्रत्येक मेयली राज्य मशीन के लिए एक बराबर मूर राज्य मशीन है।
मूर स्टेट मशीन
एक परिमित राज्य मशीन को मूर राज्य मशीन कहा जाता है, यदि आउटपुट केवल वर्तमान राज्यों पर निर्भर करते हैं। block diagram मूर राज्य मशीन को निम्न आकृति में दिखाया गया है।

जैसा कि चित्र में दिखाया गया है, मूर राज्य मशीन में दो भाग मौजूद हैं। वे जुझारू तर्क और स्मृति हैं। इस स्थिति में, वर्तमान इनपुट और वर्तमान स्थिति अगले राज्य निर्धारित करते हैं। इसलिए, अगले राज्यों के आधार पर, मूर राज्य मशीन आउटपुट का उत्पादन करती है। इसलिए, राज्य के संक्रमण के बाद ही आउटपुट मान्य होंगे।
state diagram मूर राज्य मशीन को निम्न आकृति में दिखाया गया है।

उपरोक्त आकृति में, चार राज्य हैं, अर्थात् ए, बी, सी और डी। इन राज्यों और संबंधित आउटपुट को हलकों के अंदर लेबल किया गया है। यहां, प्रत्येक संक्रमण पर केवल इनपुट मान लेबल किया गया है। उपरोक्त आंकड़ों में, इनपुट के मान के आधार पर प्रत्येक राज्य से दो संक्रमण होते हैं, x।
सामान्य तौर पर, मूर राज्य मशीन में आवश्यक राज्यों की संख्या Mealy राज्य मशीन में आवश्यक राज्यों की संख्या से अधिक या बराबर होती है। प्रत्येक मूर राज्य मशीन के लिए एक समान मेयली स्टेट मशीन है। इसलिए, आवश्यकता के आधार पर हम उनमें से एक का उपयोग कर सकते हैं।
हर एक digital systemदो भागों में विभाजित किया जा सकता है। वे डेटा पथ (डिजिटल) सर्किट और नियंत्रण सर्किट हैं। डेटा पथ सर्किट बाइनरी जानकारी (डेटा) के भंडारण और एक प्रणाली से दूसरी प्रणाली में डेटा के हस्तांतरण जैसे कार्य करते हैं। जबकि, नियंत्रण सर्किट डिजिटल सर्किट के संचालन के प्रवाह को निर्धारित करते हैं।
राज्य आरेखों का उपयोग करके बड़ी राज्य मशीनों के व्यवहार का वर्णन करना मुश्किल है। इस कठिनाई को दूर करने के लिए, एलगोरिदमिक स्टेट मशीन (एएसएम) चार्ट का उपयोग किया जा सकता है।ASM chartsफ्लो चार्ट के समान हैं। उनका उपयोग डेटा पथ सर्किट और नियंत्रण सर्किट द्वारा किए जाने वाले कार्यों के प्रवाह का प्रतिनिधित्व करने के लिए किया जाता है।
एएसएम चार्ट के बुनियादी घटक
निम्नलिखित ASM चार्ट के तीन बुनियादी घटक हैं।
- स्टेट बॉक्स
- निर्णय बॉक्स
- सशर्त उत्पादन बॉक्स
स्टेट बॉक्स
राज्य बॉक्स को आयताकार आकार में दर्शाया गया है। प्रत्येक राज्य बॉक्स अनुक्रमिक सर्किट के एक राज्य का प्रतिनिधित्व करता है। symbol राज्य बॉक्स को निम्न आकृति में दिखाया गया है।
इसमें एक प्रवेश बिंदु और एक निकास बिंदु है। राज्य का नाम राज्य बॉक्स के बाईं ओर रखा गया है। उस स्थिति के अनुरूप बिना शर्त आउटपुट को राज्य बॉक्स के अंदर रखा जा सकता है।Moore राज्य मशीन आउटपुट को राज्य बॉक्स के अंदर भी रखा जा सकता है।
निर्णय बॉक्स
निर्णय बॉक्स हीरे के आकार में दर्शाया गया है। symbol निर्णय बॉक्स को निम्न आकृति में दिखाया गया है।

इसमें एक प्रवेश बिंदु और दो निकास मार्ग हैं। इनपुट या बूलियन अभिव्यक्तियों को निर्णय बॉक्स के अंदर रखा जा सकता है, जिन्हें यह जांचना है कि वे सही हैं या गलत। यदि स्थिति सत्य है, तो वह path1 को प्राथमिकता देगा। अन्यथा, यह path2 पसंद करेगा।
सशर्त उत्पादन बॉक्स
सशर्त आउटपुट बॉक्स को अंडाकार आकार में दर्शाया गया है। symbol सशर्त आउटपुट बॉक्स को निम्न आकृति में दिखाया गया है।

इसमें एक प्रवेश बिंदु और एक निकास बिंदु राज्य बॉक्स के समान है। सशर्त आउटपुट को राज्य बॉक्स के अंदर रखा जा सकता है। सामान्य रूप में,Mealyराज्य मशीन आउटपुट को सशर्त आउटपुट बॉक्स के अंदर दर्शाया गया है। इसलिए, आवश्यकता के आधार पर, हम उपरोक्त घटकों का उपयोग ASM चार्ट बनाने के लिए ठीक से कर सकते हैं।