असतत गणित - समूह सिद्धांत
semigroup
एक परिमित या अनंत सेट $ 'S' $ एक बाइनरी ऑपरेशन के साथ $ '\ omicron' $ (रचना) को सेमीग्रुप कहा जाता है यदि यह एक साथ दो शर्तों का पालन करता है -
Closure - हर जोड़ी $ (a, b) \ _ के लिए S, \: (a \ omicron b) $ को सेट $ S $ में मौजूद होना चाहिए।
Associative - हर तत्व के लिए $ a, b, c \ _ S, (a \ omicron b) \ omicron c = a \ omicron (b \ omicron c) $ होना चाहिए।
उदाहरण
अतिरिक्त ऑपरेशन के साथ सकारात्मक पूर्णांक (शून्य को छोड़कर) का सेट एक अर्धसमूह है। उदाहरण के लिए, $ S = \ lbrace 1, 2, 3, \ dots \ rbrace $
यहाँ क्लोजर प्रॉपर्टी $ s (a, b) \ _ के लिए S, (a + b) $ के सेट S में मौजूद है। उदाहरण के लिए, S 1 $ में $ 1 + 2 = 3 \ _
साहचर्य संपत्ति भी प्रत्येक तत्व $ ए, बी, सी \ _ के लिए रखती है, (ए + बी) + सी = ए + (बी + सी) $। उदाहरण के लिए, $ (1 + 2) + 3 = 1 + (2 + 3) = 5 $
monoid
एक पहचान तत्व के साथ एक अर्धवृत्त है। एक सेट S का पहचान तत्व ($ e $ या E) द्वारा निरूपित किया गया तत्व एक ऐसा तत्व है जो $ (a \ omicron e) = a $ है, प्रत्येक तत्व के लिए $ a $ s है। एक पहचान तत्व भी कहा जाता हैunit element। तो, एक मोनोड एक साथ तीन गुण रखता है -Closure, Associative, Identity element।
उदाहरण
गुणन ऑपरेशन के साथ धनात्मक पूर्णांक (शून्य को छोड़कर) का सेट एक मोनॉयड है। $ S = \ lbrace 1, 2, 3, \ dots \ rbrace $
यहाँ क्लोजर प्रॉपर्टी प्रत्येक जोड़ी $ (a, b) \ _ के लिए S, (a a \ b b) $ के सेट के रूप में मौजूद है। [उदाहरण के लिए, $ 1 \ _ 2 = 2 \ _ में $ s और इतने पर]
साहचर्य संपत्ति भी प्रत्येक तत्व $ a, b, c \ _ S, (a a टाइम्स b) \ गुना c = a a बार (b \ टाइम्स c) $ [उदाहरण के लिए, $ (1 \ 2 2) \ गुना रखती है 3 = 1 \ गुना (2 \ 3 बार) = 6 $ और इतने पर]
पहचान संपत्ति प्रत्येक तत्व $ a, S के लिए भी रखती है, (a a times e) = a $ [उदाहरण के लिए, $ (2 \ times 1) = 2, (3 \ times 1) = 3 $ और इतने पर]। यहां पहचान तत्व 1 है।
समूह
एक समूह एक उलटा तत्व वाला एक मोनॉयड है। किसी सेट S का व्युत्क्रम तत्व (I द्वारा निरूपित) एक ऐसा तत्व है जो $ (a \ omicron I) = (I \ omicron a) = a $ है, प्रत्येक तत्व के लिए S $ में a। तो, एक समूह एक साथ चार गुण रखता है - i) बंद करना, ii) साहचर्य, iii) पहचान तत्व, iv) उलटा तत्व। एक समूह G का क्रम G में तत्वों की संख्या है और एक समूह में एक तत्व का क्रम सबसे कम धनात्मक पूर्णांक n है जो कि उस समूह G का पहचान तत्व है।
उदाहरण
$ N \ गुना N $ गैर-विलक्षण मैट्रिक्स का सेट मैट्रिक्स गुणन ऑपरेशन के तहत एक समूह बनाता है।
दो $ N \ गुना N $ non-singular matrices का उत्पाद भी एक $ N \ गुना N $ non-singular मैट्रिक्स है जो क्लोजर प्रॉपर्टी रखता है।
मैट्रिक्स गुणन ही सहयोगी है। इसलिए, साहचर्य संपत्ति रखती है।
$ N \ गुना N $ गैर-विलक्षण मैट्रिक्स के सेट में पहचान तत्व संपत्ति को धारण करने वाले पहचान मैट्रिक्स होते हैं।
जैसा कि सभी मैट्रीस गैर-विलक्षण होते हैं, उन सभी में विलोम तत्व होते हैं जो कि नॉनसिंगुलर मैट्रिस भी होते हैं। इसलिए, व्युत्क्रम संपत्ति भी रखती है।
एबेलियन ग्रुप
एक एबेलियन ग्रुप जी एक ऐसा समूह है जिसके लिए तत्व $ (a, b) \ G $ में हमेशा कम्यूटेटिव कानून रखता है। तो, एक समूह पाँच गुणों को एक साथ रखता है - i) बंद करना, ii) साहचर्य, iii) पहचान तत्व, iv) उलटा तत्व, v) कम्यूटेटिव।
उदाहरण
अतिरिक्त ऑपरेशन के साथ सकारात्मक पूर्णांक (शून्य सहित) का सेट एक एबेलियन समूह है। $ G = \ lbrace 0, 1, 2, 3, \ dots \ rbrace $
यहाँ क्लोजर प्रॉपर्टी प्रत्येक जोड़ी $ (a, b) \ _ के लिए S, (a + b) $ s सेट में मौजूद है। उदाहरण के लिए, S $ में $ 1 + 2 = 2 \ _ इत्यादि।
साहचर्य संपत्ति भी प्रत्येक तत्व $ a, b, c \ _ S, (a + b) + c = a + (b + c) $ [उदाहरण के लिए, $ (1 +2) + 3 = 1 + (2) रखती है + 3) = 6 $ इत्यादि]
पहचान संपत्ति प्रत्येक तत्व $ a, S के लिए भी रखती है, (a a times e) = a $ [उदाहरण के लिए, $ (2 \ times 1) = 2, (3 \ times 1) = 3 $ और इतने पर]। यहाँ, पहचान तत्व 1 है।
कम्यूटेटिव प्रॉपर्टी भी प्रत्येक तत्व $ a, S के लिए रखती है, (a a टाइम्स बार) = (b \ टाइम्स a) $ [उदाहरण के लिए, $ (2 \ टाइम्स 3) = (3 \ गुना 2) = 3 $ और इतने पर पर]
चक्रीय समूह और उपसमूह
ए cyclic groupएक समूह है जो एक एकल तत्व द्वारा उत्पन्न किया जा सकता है। चक्रीय समूह का प्रत्येक तत्व किसी विशिष्ट तत्व की एक शक्ति है जिसे जनरेटर कहा जाता है। जेनरेटर 'g' द्वारा एक चक्रीय समूह उत्पन्न किया जा सकता है, जैसे कि समूह के हर दूसरे तत्व को जनरेटर 'g' की शक्ति के रूप में लिखा जा सकता है।
उदाहरण
गुणन ऑपरेशन के तहत जटिल संख्या $ \ lbrace 1, -1, i, -i \ rbrace $ का सेट एक चक्रीय समूह है।
दो जनरेटर हैं - $ i $ और $ -i $ as $ i ^ 1 = i, i ^ 2 = -1, i ^ 3 = -i, i ^ 4 = 1 $ और $ भी (- i) ^ 1 = -i, (-आई) ^ 2 = -1, (-आई) ^ 3 = i, (-i) ^ 4 = 1 $ जो समूह के सभी तत्वों को शामिल करता है। इसलिए, यह एक चक्रीय समूह है।
Note - ए cyclic groupहमेशा एक एबेलियन समूह होता है लेकिन हर एबेलियन समूह एक चक्रीय समूह नहीं होता है। इसके अलावा तर्कसंगत संख्याएं चक्रीय नहीं हैं, लेकिन एबिलियन हैं।
ए subgroup H एक समूह G का उपसमूह है (यदि $ H) G $ द्वारा निरूपित किया जाता है) यदि यह एक साथ चार गुणों को संतुष्ट करता है - Closure, Associative, Identity element, तथा Inverse।
एक समूह G का एक उपसमूह H जिसमें पूरा समूह G शामिल नहीं है, एक उचित उपसमूह कहा जाता है ($ H <G $ द्वारा अस्वीकृत)। चक्रीय समूह का एक उपसमूह चक्रीय होता है और एक अबेलियन उपसमूह भी अबेलियन होता है।
उदाहरण
एक समूह $ G = \ lbrace 1, i, -1, -i \ rbrace $ दें
फिर कुछ उपसमूह $ H_1 = \ lbrace 1 \ rbrace, H_2 = \ lbrace 1, -1 \ rbrace $,
यह उपसमूह नहीं है - $ H_3 = \ lbrace 1, i \ rbrace $ क्योंकि वह $ (i) ^ {- 1} = -i $ $ H_3 $ में नहीं है
आंशिक रूप से ऑर्डर किया गया सेट (POSET)
एक आंशिक रूप से आदेशित सेट में एक द्विआधारी संबंध के साथ एक सेट होता है जो रिफ्लेक्सिव, एंटीसिमेट्रिक और ट्रांसीवर होता है। "आंशिक रूप से ऑर्डर किया गया सेट" POSET के रूप में संक्षिप्त है।
उदाहरण
बाइनरी ऑपरेशन के तहत वास्तविक संख्याओं का सेट $ (\ le) $ से कम या उसके बराबर है।
सेट $ S = \ lbrace 1, 2, 3 \ rbrace $ और ऑपरेशन $ \ le $ है
संबंध $ \ lbrace (1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3) \ rbrace $ होंगे
यह संबंध R $ \ lbrace (1, 1), (2, 2), (3, 3) \ rbrace \ के रूप में Reflexive है R $ में
यह संबंध आर सममिति है, जैसा कि
$ \ lbrace (1, 2), (1, 3), (2, 3) \ rbrace \ "R \ और \ lbrace (1, 2), (1, 3), (2, 3) \ rbrace ∉ में R $
यह रिश्ता R $ $ में lbrace (1,2), (2,3), (1,3) \ rbrace \ के रूप में भी सकर्मक है।
इसलिए, यह एक है poset।
ऑपरेशन 'रीचैबिलिटी' के तहत एक निर्देशित चक्रीय ग्राफ का शीर्ष सेट एक पोसैट है।
हेस आरेख
एक पोज़ेट का हेज़ आरेख एक निर्देशित ग्राफ़ होता है जिसका वर्टिकल उस पॉज़ेट का तत्व होता है और आर्क्स पोज़ में जोड़े (x, y) को कवर करता है। यदि पोसेट $ x <y $ में है, तो बिंदु x हसे चित्र में बिंदु y से कम दिखाई देता है। यदि पॉस में $ x <y <z $ है, तो एक्स और जेड के बीच तीर नहीं दिखाया गया है क्योंकि यह निहित है।
उदाहरण
$ \ Lbrace 1, 2, 3 \ rbrace = \ lbrace \ emptyset, \ lbrace 1 \ rbrace, \ lbrace 2 \ rbrace, \ lbrace \ \ rbrace, \ lbrace 1, 2 \ rbrace, \ lbrace 1 के उप-वर्ग की स्थिति , 3 \ rbrace, \ lbrace 2, 3 \ rbrace, \ lbrace 1, 2, 3 \ rbrace \ rbrace $ को निम्नलिखित हसी चित्र द्वारा दिखाया गया है -
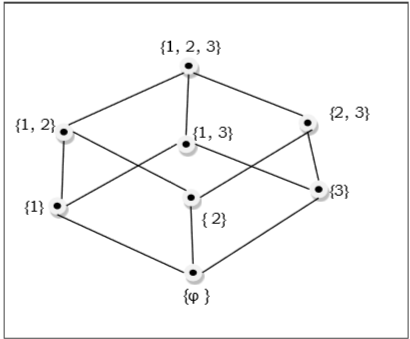
रैखिक आदेशित सेट
रेखीय रूप से ऑर्डर किया गया सेट या कुल ऑर्डर किया गया सेट एक आंशिक ऑर्डर सेट है जिसमें तत्व की प्रत्येक जोड़ी तुलनीय है। तत्व $ a, b \ _ S $ में तुलनीय हैं यदि $ a \ le b $ या $ b \ le $ धारण किया जाता है। ट्राइकोटॉमी कानून इस कुल निर्धारित सेट को परिभाषित करता है। एक पूरी तरह से ऑर्डर किए गए सेट को एक वितरण जाली के रूप में परिभाषित किया जा सकता है, जिसमें संपत्ति $ \ lbrace a \ lor b, a \ land b \ rbrace = \ lbrace a, b \ rbrace $ सभी के सेट और b के सभी मानों के लिए सेट होती है।
उदाहरण
$ \ Lbrace a, b \ rbrace $ के आदेश की शक्तियां \ subseteq द्वारा पूरी तरह से ऑर्डर की गई शक्ति के सभी तत्वों के रूप में सेट होती हैं $ P = \ lbrace \ emptyset, \ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace a, b \ rbrace \ rbrace $ तुलनीय हैं।
गैर-कुल आदेश सेट का उदाहरण
एक सेट $ S = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ ऑपरेशन x डिवाइसेस y के तहत कुल ऑर्डर किया गया सेट नहीं है।
यहाँ, सभी $ (x, y) \ _ के लिए S, x | y $ को पकड़ना है लेकिन यह सच नहीं है कि 2 | 3, जैसा कि 2 विभाजित नहीं करता है 3 या 3 विभाजित नहीं करता है। इसलिए, यह कुल आदेशित सेट नहीं है।
जाली
एक जाली एक पोज़ेट $ (L, \ le) $ है, जिसके लिए L $ में हर जोड़ी $ \ lbrace a, b \ rbrace \ की कम से कम ऊपरी सीमा होती है ($ a \ lor b $ द्वारा निरूपित) और एक महानतम बाध्य ( $ a \ land b $ द्वारा निरूपित)। LUB $ (\ lbrace a, b \ rbrace) $ को a और b का जोड़ कहा जाता है। GLB $ (\ lbrace a, b \ rbrace) $ को a और b का मिलना कहा जाता है।
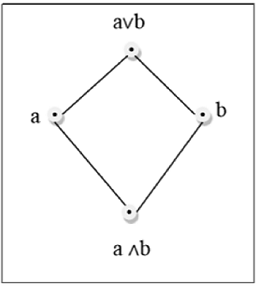
उदाहरण
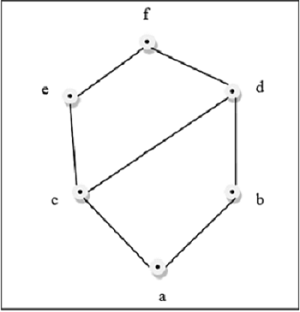
यह उपरोक्त आंकड़ा एक जाली है, क्योंकि प्रत्येक जोड़ी के लिए L $, a, b \ rbrace \ में L $, एक GLB और एक LUB मौजूद है।
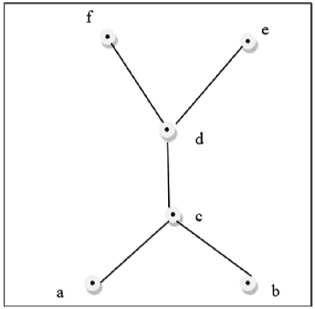
यह उपरोक्त आंकड़ा एक जाली नहीं है क्योंकि $ GLB (a, b) $ और $ LUB (e, f) $ मौजूद नहीं है।
कुछ अन्य अक्षांशों की चर्चा नीचे की गई है -
बंधे हुए जाली
एक जाली L एक बंधी हुई जाली बन जाती है अगर उसमें सबसे बड़ा तत्व 1 और सबसे कम तत्व 0 हो।
लागू किया गया जाली
एक जाली एल एक पूरक जाली बन जाता है यदि यह एक बंधी हुई जाली है और यदि जाली के प्रत्येक तत्व का पूरक है। एक तत्व x में एक पूरक x 'है अगर $ \ अस्तित्व x (x \ भूमि x' = 0 और x \ lor x '= 1 $)
वितरण योग्य जाली
यदि एक जाली निम्नलिखित दो वितरण गुणों को संतुष्ट करती है, तो इसे वितरण जाली कहा जाता है।
$ a \ lor (b \ land c) = (a \ lor b) \ land (a \ lor c) $
$ a \ _ भूमि (b \ lor c) = (a \ land b) \ lor (a \ land c) $
मॉड्यूलर जाली
यदि एक जाली निम्नलिखित संपत्ति को संतुष्ट करती है, तो इसे मॉड्यूलर जाली कहा जाता है।
$ a भूमि (b \ lor (a land भूमि)) = (a (भूमि b) \ lor (a \ d d) $
लत्ती के गुण
इम्पोटोटेंट गुण
$ a \ lor a = a $ है
$ a \ भूमि a = a $
अवशोषण गुण
$ a \ lor (a a land b) = a $
$ a \ _ (a \ lor b) = a $
कम्यूटेटिव गुण
$ a \ lor b = b \ lor a $ है
$ a \ भूमि b = b \ land एक $
सहयोगी गुण
$ a \ lor (b \ lor c) = (a \ lor b) \ lor c $
$ a भूमि (b \ भूमि c) = (a \ land b) \ भूमि c $
एक जाली का दोहरी
एक जाली का दोहरी '$ \ lor $' और '$' भूमि $ 'के संचालन को रोककर प्राप्त किया जाता है।
उदाहरण
$ \ Lbrack a \ lor (b \ land c) \ rbrack \ is \ \ lbrack a \ land (b \ lor c) \ rbrack $ का दोहरी