असतत गणित - त्वरित गाइड
गणित को मोटे तौर पर दो श्रेणियों में वर्गीकृत किया जा सकता है -
Continuous Mathematics- यह निरंतर संख्या रेखा या वास्तविक संख्याओं पर आधारित है। यह इस तथ्य से विशेषता है कि किसी भी दो संख्याओं के बीच, लगभग हमेशा संख्याओं का एक अनंत सेट होता है। उदाहरण के लिए, निरंतर गणित में एक फ़ंक्शन को बिना टूटे एक चिकनी वक्र में प्लॉट किया जा सकता है।
Discrete Mathematics- इसमें अलग-अलग मूल्य शामिल हैं; यानी किन्हीं दो बिंदुओं के बीच, अंकों की संख्या होती है। उदाहरण के लिए, यदि हमारे पास वस्तुओं का एक निश्चित सेट है, तो फ़ंक्शन को इन ऑब्जेक्ट्स के ऑर्डर किए गए जोड़े की सूची के रूप में परिभाषित किया जा सकता है, और उन जोड़े की पूरी सूची के रूप में प्रस्तुत किया जा सकता है।
गणित में विषय
हालांकि असतत गणित की शाखाओं की निश्चित संख्या नहीं हो सकती है, इस विषय के बारे में निम्नलिखित विषय किसी भी अध्ययन में लगभग हमेशा शामिल हैं -
- सेट, संबंध और कार्य
- गणितीय तर्क
- समूह सिद्धांत
- गिनती की थ्योरी
- Probability
- गणितीय प्रेरण और पुनरावृत्ति संबंध
- ग्राफ सिद्धांत
- Trees
- बूलियन बीजगणित
हम इस ट्यूटोरियल के बाद के अध्यायों में से प्रत्येक पर चर्चा करेंगे।
जर्मन गणितज्ञ G. Cantorसेट की अवधारणा शुरू की। उन्होंने एक सेट को कुछ नियमों या विवरण के माध्यम से चयनित निश्चित और अलग-अलग वस्तुओं के संग्रह के रूप में परिभाषित किया था।
Setसिद्धांत अध्ययन के कई अन्य क्षेत्रों का आधार बनाता है जैसे गिनती सिद्धांत, संबंध, ग्राफ सिद्धांत और परिमित राज्य मशीनें। इस अध्याय में, हम विभिन्न पहलुओं को कवर करेंगेSet Theory।
सेट - परिभाषा
एक सेट विभिन्न तत्वों का एक अनियंत्रित संग्रह है। सेट ब्रैकेट का उपयोग करके इसके तत्वों को सूचीबद्ध करके एक सेट स्पष्ट रूप से लिखा जा सकता है। यदि तत्वों के क्रम को बदल दिया जाता है या सेट के किसी भी तत्व को दोहराया जाता है, तो यह सेट में कोई बदलाव नहीं करता है।
सेट्स के कुछ उदाहरण
- सभी धनात्मक पूर्णांक का एक सेट
- सौर मंडल के सभी ग्रहों का एक समूह
- भारत में सभी राज्यों का एक समूह
- वर्णमाला के सभी निचले अक्षरों का एक सेट
एक सेट का प्रतिनिधित्व
सेट को दो तरीकों से दर्शाया जा सकता है -
- रोस्टर या सारणीबद्ध रूप
- बिल्डर संकेतन सेट करें
रोस्टर या सारणीबद्ध रूप
सेट में सभी तत्वों को सूचीबद्ध करके इसे दर्शाया गया है। तत्वों को ब्रेसिज़ के भीतर संलग्न किया गया है और कॉमा द्वारा अलग किया गया है।
Example 1 - अंग्रेजी वर्णमाला में स्वरों का सेट, $A = \lbrace a,e,i,o,u \rbrace$
Example 2 - 10 से कम विषम संख्याओं का सेट, $B = \lbrace 1,3,5,7,9 \rbrace$
बिल्डर संकेतन सेट करें
सेट को एक संपत्ति को निर्दिष्ट करके परिभाषित किया जाता है जो सेट के तत्वों में आम है। सेट के रूप में वर्णित है$A = \lbrace x : p(x) \rbrace$
Example 1 - सेट $\lbrace a,e,i,o,u \rbrace$ के रूप में लिखा है -
$A = \lbrace x : \text{x is a vowel in English alphabet} \rbrace$
Example 2 - सेट $\lbrace 1,3,5,7,9 \rbrace$ के रूप में लिखा है -
$B = \lbrace x : 1 \le x \lt 10 \ and\ (x \% 2) \ne 0 \rbrace$
यदि एक तत्व x किसी भी सेट S का सदस्य है, तो इसे निरूपित किया जाता है $x \in S$ और यदि कोई तत्व y सेट S का सदस्य नहीं है, तो वह इसके द्वारा निरूपित होता है $y \notin S$।
Example- अगर$S = \lbrace1, 1.2, 1.7, 2\rbrace , 1 \in S$ परंतु $1.5 \notin S$
कुछ महत्वपूर्ण सेट
N - सभी प्राकृतिक संख्याओं का समुच्चय = $\lbrace1, 2, 3, 4, .....\rbrace$
Z - सभी पूर्णांकों का सेट = $\lbrace....., -3, -2, -1, 0, 1, 2, 3, .....\rbrace$
Z+ - सभी सकारात्मक पूर्णांकों का सेट
Q - सभी तर्कसंगत संख्याओं का समूह
R - सभी वास्तविक संख्याओं का सेट
W - सभी पूरे नंबरों का सेट
एक सेट की कार्डिनैलिटी
एक सेट S की कार्डिनैलिटी, द्वारा निरूपित $|S|$, सेट के तत्वों की संख्या है। संख्या को कार्डिनल संख्या भी कहा जाता है। यदि सेट में तत्वों की अनंत संख्या है, तो इसकी कार्डिनैलिटी है$\infty$।
Example - $|\lbrace 1, 4, 3, 5 \rbrace | = 4, | \lbrace 1, 2, 3, 4, 5, \dots \rbrace | = \infty$
यदि दो सेट X और Y हैं,
$|X| = |Y|$दो सेट X और Y समान कार्डिनैलिटी दर्शाता है। यह तब होता है जब X में तत्वों की संख्या Y में तत्वों की संख्या के बराबर होती है। इस मामले में, X से Y तक एक जीवनी संबंधी फ़ंक्शन 'f' मौजूद होता है।
$|X| \le |Y|$यह दर्शाता है कि सेट X की कार्डिनैलिटी, Y की कार्डिनैलिटी से कम या बराबर है। यह तब होता है जब X में तत्वों की संख्या Y के बराबर या उससे कम होती है। यहां, X से Y तक एक इंजेक्शन फ़ंक्शन 'f' मौजूद है।
$|X| \lt |Y|$यह दर्शाता है कि सेट X की कार्डिनैलिटी सेट Y की कार्डिनैलिटी से कम है। यह तब होता है जब X में तत्वों की संख्या Y की तुलना में कम होती है। यहाँ, X से Y तक फ़ंक्शन 'f' इंजेक्शन फ़ंक्शन है, लेकिन विशेषण नहीं है।
$If\ |X| \le |Y|$ तथा $|X| \ge |Y|$ फिर $|X| = |Y|$। सेट X और Y को आमतौर पर समकक्ष सेट के रूप में जाना जाता है।
सेट के प्रकार
सेटों को कई प्रकारों में वर्गीकृत किया जा सकता है। जिनमें से कुछ परिमित, अनंत, सबसेट, सार्वभौमिक, उचित, सिंगलटन सेट आदि हैं।
परिमित सेट
एक सेट जिसमें तत्वों की निश्चित संख्या होती है, एक परिमित सेट कहलाता है।
Example - $S = \lbrace x \:| \:x \in N$ तथा $70 \gt x \gt 50 \rbrace$
अनंत सेट
एक सेट जिसमें अनंत संख्या में तत्व होते हैं उसे अनंत सेट कहा जाता है।
Example - $S = \lbrace x \: | \: x \in N $ तथा $ x \gt 10 \rbrace$
सबसेट
एक सेट X सेट Y का एक उपसमूह है (जैसा लिखा गया है $X \subseteq Y$) यदि X का प्रत्येक तत्व सेट Y का एक तत्व है।
Example 1 - चलो $X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ तथा $Y = \lbrace 1, 2 \rbrace$। यहाँ सेट Y सेट X का एक सबसेट है क्योंकि सेट Y के सभी तत्व सेट X में हैं। इसलिए, हम लिख सकते हैं$Y \subseteq X$।
Example 2 - चलो $X = \lbrace 1, 2, 3 \rbrace$ तथा $Y = \lbrace 1, 2, 3 \rbrace$। यहाँ सेट Y, सेट X का एक सबसेट (उचित उपसमूह नहीं) है क्योंकि सेट Y के सभी तत्व सेट X में है। इसलिए, हम लिख सकते हैं$Y \subseteq X$।
उचित सबसेट
शब्द "उचित सबसेट" को "सबसेट नहीं बल्कि बराबर" के रूप में परिभाषित किया जा सकता है। एक सेट X सेट Y का उचित उपसमूह है (जैसा लिखा गया है$ X \subset Y $) यदि X का प्रत्येक तत्व सेट Y और का एक तत्व है $|X| \lt |Y|$।
Example - चलो $X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ तथा $Y = \lbrace 1, 2 \rbrace$। यहाँ सेट करें$Y \subset X$ में सभी तत्वों के बाद से $Y$ में समाहित हैं $X$ भी और $X$ कम से कम एक तत्व सेट से अधिक है $Y$।
सार्वसमुच्चय
यह किसी विशेष संदर्भ या अनुप्रयोग में सभी तत्वों का एक संग्रह है। उस संदर्भ या अनुप्रयोग के सभी सेट अनिवार्य रूप से इस सार्वभौमिक सेट के सबसेट हैं। यूनिवर्सल सेट के रूप में प्रतिनिधित्व किया है$U$।
Example - हम परिभाषित कर सकते हैं $U$पृथ्वी पर सभी जानवरों के सेट के रूप में। इस मामले में, सभी स्तनधारियों का सेट सबसेट है$U$, सभी मछलियों का सेट एक सबसेट है $U$, सभी कीड़ों का सेट एक सबसेट है $U$, और इसी तरह।
खाली सेट या अशक्त सेट
एक खाली सेट में कोई तत्व नहीं होते हैं। इसके द्वारा निरूपित किया जाता है$\emptyset$। जैसे खाली सेट में तत्वों की संख्या परिमित होती है, वैसे ही खाली सेट एक परिमित सेट होता है। खाली सेट या अशक्त सेट की कार्डिनैलिटी शून्य है।
Example - $S = \lbrace x \:| \: x \in N$ तथा $7 \lt x \lt 8 \rbrace = \emptyset$
सिंगलटन सेट या यूनिट सेट
सिंगलटन सेट या यूनिट सेट में केवल एक तत्व होता है। एक सिंगलटन सेट द्वारा चिह्नित किया जाता है$\lbrace s \rbrace$।
Example - $S = \lbrace x \:| \:x \in N,\ 7 \lt x \lt 9 \rbrace$ = $\lbrace 8 \rbrace$
समान सेट
यदि दो सेटों में समान तत्व होते हैं तो उन्हें समान कहा जाता है।
Example - अगर $A = \lbrace 1, 2, 6 \rbrace$ तथा $B = \lbrace 6, 1, 2 \rbrace$, वे समान हैं क्योंकि सेट A का प्रत्येक तत्व सेट B का एक तत्व है और सेट B का प्रत्येक तत्व सेट A का एक तत्व है।
समतुल्य सेट
यदि दो सेटों की कार्डिनैलिटी समान हैं, तो उन्हें समकक्ष सेट कहा जाता है।
Example - अगर $A = \lbrace 1, 2, 6 \rbrace$ तथा $B = \lbrace 16, 17, 22 \rbrace$, वे समान हैं क्योंकि A की कार्डिनैलिटी B की कार्डिनैलिटी के बराबर है $|A| = |B| = 3$
ओवरलैपिंग सेट
कम से कम एक सामान्य तत्व वाले दो सेटों को ओवरलैपिंग सेट कहा जाता है।
ओवरलैपिंग सेट के मामले में -
$n(A \cup B) = n(A) + n(B) - n(A \cap B)$
$n(A \cup B) = n(A - B) + n(B - A) + n(A \cap B)$
$n(A) = n(A - B) + n(A \cap B)$
$n(B) = n(B - A) + n(A \cap B)$
Example - चलो $A = \lbrace 1, 2, 6 \rbrace$ तथा $B = \lbrace 6, 12, 42 \rbrace$। एक सामान्य तत्व '6' है, इसलिए ये सेट ओवरलैपिंग सेट हैं।
सेट को खारिज करें
दो सेट ए और बी को डिसऑइंट सेट कहा जाता है यदि उनके पास एक तत्व भी नहीं है। इसलिए, disjoint सेट के निम्नलिखित गुण हैं -
$n(A \cap B) = \emptyset$
$n(A \cup B) = n(A) + n(B)$
Example - चलो $A = \lbrace 1, 2, 6 \rbrace$ तथा $B = \lbrace 7, 9, 14 \rbrace$, एक भी सामान्य तत्व नहीं है, इसलिए ये सेट ओवरलैपिंग सेट हैं।
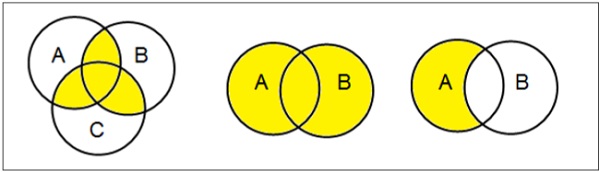
वेन डायग्राम
जॉन वेन द्वारा 1880 में आविष्कार किया गया वेन आरेख, एक योजनाबद्ध आरेख है जो विभिन्न गणितीय सेटों के बीच सभी संभावित तार्किक संबंधों को दर्शाता है।
Examples
संचालन सेट करें
सेट ऑपरेशंस में सेट यूनियन, सेट इन्टरसेशन, सेट डिफरेंस, सेट का पूरक और कार्टेशियन प्रोडक्ट शामिल हैं।
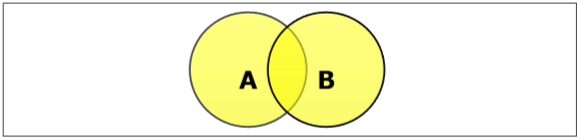
यूनियन सेट करें
सेट ए और बी के संघ (द्वारा चिह्नित) $A \cup B$) तत्वों का वह समूह है जो A, B या A और B दोनों में है, इसलिए $A \cup B = \lbrace x \:| \: x \in A\ OR\ x \in B \rbrace$।
Example - अगर $A = \lbrace 10, 11, 12, 13 \rbrace$ और बी = $\lbrace 13, 14, 15 \rbrace$, फिर $A \cup B = \lbrace 10, 11, 12, 13, 14, 15 \rbrace$। (सामान्य तत्व केवल एक बार होता है)
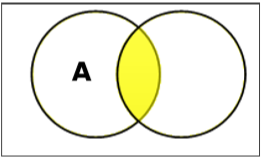
अंतःकरण सेट करें
सेट ए और बी के अंतर (द्वारा चिह्नित) $A \cap B$) तत्वों का एक सेट है जो ए और बी दोनों में हैं इसलिए, $A \cap B = \lbrace x \:|\: x \in A\ AND\ x \in B \rbrace$।
Example - अगर $A = \lbrace 11, 12, 13 \rbrace$ तथा $B = \lbrace 13, 14, 15 \rbrace$, फिर $A \cap B = \lbrace 13 \rbrace$।
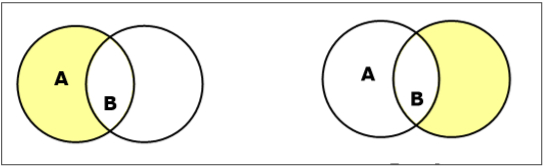
अंतर / सापेक्ष पूरक सेट करें
सेट ए और बी के अंतर (द्वारा चिह्नित) $A – B$) तत्वों का वह समूह है जो केवल A में होता है लेकिन B. में नहीं। $A - B = \lbrace x \:| \: x \in A\ AND\ x \notin B \rbrace$।
Example - अगर $A = \lbrace 10, 11, 12, 13 \rbrace$ तथा $B = \lbrace 13, 14, 15 \rbrace$, फिर $(A - B) = \lbrace 10, 11, 12 \rbrace$ तथा $(B - A) = \lbrace 14, 15 \rbrace$। यहां, हम देख सकते हैं$(A - B) \ne (B - A)$
एक सेट के पूरक
एक सेट ए के पूरक (द्वारा चिह्नित) $A’$) उन तत्वों का समूह है जो सेट ए में नहीं हैं। इसलिए, $A' = \lbrace x | x \notin A \rbrace$।
अधिक विशेष रूप से, $A'= (U - A)$ कहाँ पे $U$ एक सार्वभौमिक सेट है जिसमें सभी ऑब्जेक्ट शामिल हैं।
Example - अगर $A = \lbrace x \:| \: x\ \: {belongs\: to\: set\: of\: odd \:integers} \rbrace$ फिर $A' = \lbrace y\: | \: y\ \: {does\: not\: belong\: to\: set\: of\: odd\: integers } \rbrace$
कार्टेशियन उत्पाद / क्रॉस उत्पाद
सेट के n संख्या का कार्टेशियन उत्पाद $A_1, A_2, \dots A_n$ इस रूप में घोषित किया गया $A_1 \times A_2 \dots \times A_n$ सभी संभव आदेश दिए गए जोड़े के रूप में परिभाषित किया जा सकता है $(x_1, x_2, \dots x_n)$ कहाँ पे $x_1 \in A_1, x_2 \in A_2, \dots x_n \in A_n$
Example - अगर हम दो सेट लेते हैं $A = \lbrace a, b \rbrace$ तथा $B = \lbrace 1, 2 \rbrace$,
ए और बी के कार्टेशियन उत्पाद के रूप में लिखा गया है - $A \times B = \lbrace (a, 1), (a, 2), (b, 1), (b, 2)\rbrace$
बी और ए के कार्टेशियन उत्पाद के रूप में लिखा गया है - $B \times A = \lbrace (1, a), (1, b), (2, a), (2, b)\rbrace$
सत्ता स्थापित
एक सेट S का पावर सेट खाली सेट सहित S के सभी सबसेट का सेट है। कार्डिनैलिटी n के एक सेट S के पावर सेट की कार्डिनैलिटी है$2^n$। पावर सेट को चिह्नित किया जाता है$P(S)$।
Example −
एक सेट के लिए $S = \lbrace a, b, c, d \rbrace$ आइए हम सबसेट की गणना करते हैं -
0 तत्वों के साथ ग्राहकी - $\lbrace \emptyset \rbrace$ (खाली सेट)
1 तत्व के साथ ग्राहकी - $\lbrace a \rbrace, \lbrace b \rbrace, \lbrace c \rbrace, \lbrace d \rbrace$
2 तत्वों के साथ ग्राहकी - $\lbrace a, b \rbrace, \lbrace a,c \rbrace, \lbrace a, d \rbrace, \lbrace b, c \rbrace, \lbrace b,d \rbrace,\lbrace c,d \rbrace$
3 तत्वों के साथ ग्राहकी - $\lbrace a ,b, c\rbrace,\lbrace a, b, d \rbrace, \lbrace a,c,d \rbrace,\lbrace b,c,d \rbrace$
4 तत्वों के साथ ग्राहकी - $\lbrace a, b, c, d \rbrace$
इसलिये, $P(S)=$
$\lbrace \quad \lbrace \emptyset \rbrace, \lbrace a \rbrace, \lbrace b \rbrace, \lbrace c \rbrace, \lbrace d \rbrace, \lbrace a,b \rbrace, \lbrace a,c \rbrace, \lbrace a,d \rbrace, \lbrace b,c \rbrace, \lbrace b,d \rbrace, \lbrace c,d \rbrace, \lbrace a,b,c \rbrace, \lbrace a,b,d \rbrace, \lbrace a,c,d \rbrace, \lbrace b,c,d \rbrace, \lbrace a,b,c,d \rbrace \quad \rbrace$
$| P(S) | = 2^4 = 16$
Note - खाली सेट का पावर सेट भी एक खाली सेट है।
$| P (\lbrace \emptyset \rbrace) | = 2^0 = 1$
एक सेट का विभाजन
एक सेट के विभाजन का कहना है कि एस , का एक संग्रह है n संबंध तोड़ना सबसेट, कहते हैं$P_1, P_2, \dots P_n$ यह निम्नलिखित तीन स्थितियों को संतुष्ट करता है -
$P_i$ खाली सेट शामिल नहीं है।
$\lbrack P_i \ne \lbrace \emptyset \rbrace\ for\ all\ 0 \lt i \le n \rbrack$
सबसेट का संघ पूरे मूल सेट के बराबर होना चाहिए।
$\lbrack P_1 \cup P_2 \cup \dots \cup P_n = S \rbrack$
किन्हीं दो अलग-अलग सेटों का अंतरच्छेदन खाली है।
$\lbrack P_a \cap P_b = \lbrace \emptyset \rbrace,\ for\ a \ne b\ where\ n \ge a,\: b \ge 0 \rbrack$
Example
लश्कर $S = \lbrace a, b, c, d, e, f, g, h \rbrace$
एक संभावित विभाजन है $\lbrace a \rbrace, \lbrace b, c, d \rbrace, \lbrace e, f, g, h \rbrace$
एक और संभावित विभाजन है $\lbrace a, b \rbrace, \lbrace c, d \rbrace, \lbrace e, f, g, h \rbrace$
बेल नंबर
बेल नंबर एक सेट को विभाजित करने के तरीकों की संख्या की गिनती देते हैं। उनके द्वारा निरूपित किया जाता है$B_n$ जहां n सेट की कार्डिनैलिटी है।
Example -
लश्कर $S = \lbrace 1, 2, 3\rbrace$, $n = |S| = 3$
वैकल्पिक विभाजन हैं -
1। $\emptyset , \lbrace 1, 2, 3 \rbrace$
2। $\lbrace 1 \rbrace , \lbrace 2, 3 \rbrace$
3। $\lbrace 1, 2 \rbrace , \lbrace 3 \rbrace$
4। $\lbrace 1, 3 \rbrace , \lbrace 2 \rbrace$
5। $\lbrace 1 \rbrace , \lbrace 2 \rbrace , \lbrace 3 \rbrace$
इसलिये $B_3 = 5$
जब भी सेट पर चर्चा की जा रही है, सेट के तत्वों के बीच संबंध अगली चीज है जो सामने आती है। Relations एक ही सेट की वस्तुओं के बीच या दो या अधिक सेट की वस्तुओं के बीच मौजूद हो सकता है।
परिभाषा और गुण
सेट x से y तक एक बाइनरी रिलेशन R (जैसा लिखा गया है $xRy$ या $R(x,y)$) कार्टेशियन उत्पाद का एक सबसेट है $x \times y$। यदि जी की आदेशित जोड़ी उलट जाती है, तो संबंध भी बदल जाता है।
आम तौर पर सेट के बीच एक एन-एरी रिश्ता आर $A_1, \dots ,\ and\ A_n$ एन-आर्य उत्पाद का एक सबसेट है $A_1 \times \dots \times A_n$। एक संबंध R की न्यूनतम कार्डिनैलिटी शून्य है और अधिकतम है$n^2$ इस मामले में।
एक एकल सेट ए पर एक द्विआधारी संबंध आर का एक सबसेट है $A \times A$।
दो अलग-अलग सेटों के लिए, A और B, क्रमशः कार्डिनैलिटी m और n वाले हैं, A से B तक के संबंध R की अधिकतम कार्डिनैलिटी mn है ।
डोमेन और सीमा
यदि दो सेट ए और बी हैं, और संबंध आर में ऑर्डर पेयर (x, y) है, तो -
domain आर, डोम (आर) का सेट है $\lbrace x \:| \: (x, y) \in R \:for\: some\: y\: in\: B \rbrace$
range , R, Ran (R) का सेट है $\lbrace y\: |\: (x, y) \in R \:for\: some\: x\: in\: A\rbrace$
उदाहरण
चलो, $A = \lbrace 1, 2, 9 \rbrace $ तथा $ B = \lbrace 1, 3, 7 \rbrace$
केस 1 - अगर रिलेशन 'आर' के बराबर है $R = \lbrace (1, 1), (3, 3) \rbrace$
डोम (R) = $\lbrace 1, 3 \rbrace , Ran(R) = \lbrace 1, 3 \rbrace$
केस 2 - यदि रिश्ता R 'से कम' है $R = \lbrace (1, 3), (1, 7), (2, 3), (2, 7) \rbrace$
डोम (R) = $\lbrace 1, 2 \rbrace , Ran(R) = \lbrace 3, 7 \rbrace$
केस 3 - यदि संबंध R 'से अधिक है' तो $R = \lbrace (2, 1), (9, 1), (9, 3), (9, 7) \rbrace$
डोम (R) = $\lbrace 2, 9 \rbrace , Ran(R) = \lbrace 1, 3, 7 \rbrace$
ग्राफ़ का उपयोग करके संबंधों का प्रतिनिधित्व
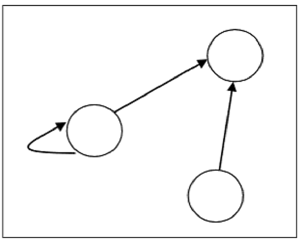
एक निर्देशित ग्राफ का उपयोग करके एक संबंध का प्रतिनिधित्व किया जा सकता है।
ग्राफ़ में कोने की संख्या उस सेट में तत्वों की संख्या के बराबर है जहां से संबंध को परिभाषित किया गया है। संबंध आर में प्रत्येक आदेशित जोड़ी (x, y) के लिए, शीर्ष 'x' से 'y' के लिए निर्देशित धार होगी। यदि एक आदेशित जोड़ी (x, x) है, तो 'x' शीर्ष पर स्व-लूप होगा।
मान लीजिए, एक रिश्ता है $R = \lbrace (1, 1), (1,2), (3, 2) \rbrace$ सेट पर $S = \lbrace 1, 2, 3 \rbrace$, इसे निम्नलिखित ग्राफ द्वारा दर्शाया जा सकता है -
संबंधों के प्रकार
Empty Relation सेट X और Y के बीच, या E पर, खाली सेट है $\emptyset$
Full Relation सेट X और Y के बीच का सेट है $X \times Y$
Identity Relation सेट X पर सेट है $\lbrace (x, x) | x \in X \rbrace$
एक संबंध R के व्युत्क्रम संबंध R को इस प्रकार परिभाषित किया गया है - $R' = \lbrace (b, a) | (a, b) \in R \rbrace$
Example - अगर $R = \lbrace (1, 2), (2, 3) \rbrace$ फिर $R' $ होगा $\lbrace (2, 1), (3, 2) \rbrace$
सेट A पर एक संबंध R को कहा जाता है Reflexive अगर $\forall a \in A$ से संबंधित है (aRa होल्ड)
Example - संबंध $R = \lbrace (a, a), (b, b) \rbrace$ सेट पर $X = \lbrace a, b \rbrace$ पलटा हुआ है।
सेट A पर एक संबंध R को कहा जाता है Irreflexive यदि नही $a \in A$ एक से संबंधित है (aRa पकड़ नहीं है)।
Example - संबंध $R = \lbrace (a, b), (b, a) \rbrace$ सेट पर $X = \lbrace a, b \rbrace$ अकाट्य है।
सेट A पर एक संबंध R को कहा जाता है Symmetric अगर $xRy$ का तात्पर्य $yRx$, $\forall x \in A$ तथा $\forall y \in A$।
Example - संबंध $R = \lbrace (1, 2), (2, 1), (3, 2), (2, 3) \rbrace$ सेट पर $A = \lbrace 1, 2, 3 \rbrace$ सममित है।
सेट A पर एक संबंध R को कहा जाता है Anti-Symmetric अगर $xRy$ तथा $yRx$ का तात्पर्य $x = y \: \forall x \in A$ तथा $\forall y \in A$।
Example - संबंध $R = \lbrace (x, y)\to N |\:x \leq y \rbrace$ तब से विरोधी सममित है $x \leq y$ तथा $y \leq x$ का तात्पर्य $x = y$।
सेट A पर एक संबंध R को कहा जाता है Transitive अगर $xRy$ तथा $yRz$ का तात्पर्य $xRz, \forall x,y,z \in A$।
Example - संबंध $R = \lbrace (1, 2), (2, 3), (1, 3) \rbrace$ सेट पर $A = \lbrace 1, 2, 3 \rbrace$ सकर्मक है।
एक रिश्ता एक है Equivalence Relation यदि यह प्रतिवर्ती, सममित और संक्रमणीय है।
Example - संबंध $R = \lbrace (1, 1), (2, 2), (3, 3), (1, 2), (2,1), (2,3), (3,2), (1,3), (3,1) \rbrace$ सेट पर $A = \lbrace 1, 2, 3 \rbrace$ एक समतुल्य संबंध है क्योंकि यह प्रतिवर्ती, सममितीय और सकर्मक है।
ए Functionसेट के प्रत्येक तत्व को असाइन करता है, संबंधित सेट का ठीक एक तत्व। फ़ंक्शंस विभिन्न क्षेत्रों में एल्गोरिदम की कम्प्यूटेशनल जटिलता का प्रतिनिधित्व, वस्तुओं की गिनती, अनुक्रमों और तारों के अध्ययन, कुछ का नाम देने के लिए उनके आवेदन को ढूंढते हैं। इस भाग का तीसरा और अंतिम अध्याय कार्यों के महत्वपूर्ण पहलुओं पर प्रकाश डालता है।
कार्य - परिभाषा
एक समारोह या मानचित्रण (के रूप में परिभाषित) $f: X \rightarrow Y$) एक सेट एक्स के तत्वों से दूसरे सेट वाई के तत्वों (एक्स और वाई गैर-खाली सेट हैं) से एक संबंध है। X को डोमेन कहा जाता है और Y को फ़ंक्शन 'f' का कोडोमैन कहा जाता है।
समारोह 'एफ' एक्स और वाई पर एक संबंध है जैसे कि प्रत्येक के लिए $x \in X$, वहाँ एक अद्वितीय मौजूद है $y \in Y$ ऐसा है कि $(x,y) \in R$। 'x' को प्री-इमेज कहा जाता है और 'y' को फंक्शन एफ की इमेज कहा जाता है।
एक फ़ंक्शन एक से एक या कई से एक हो सकता है लेकिन एक से कई नहीं।
विशेषण / एक-से-एक फ़ंक्शन
एक समारोह $f: A \rightarrow B$ इंजेक्शन या एक-से-एक फ़ंक्शन है यदि प्रत्येक के लिए $b \in B$, वहाँ सबसे अधिक एक में मौजूद है $a \in A$ ऐसा है कि $f(s) = t$।
इसका मतलब एक फंक्शन है f अगर इंजेक्शन है $a_1 \ne a_2$ का तात्पर्य $f(a1) \ne f(a2)$।
उदाहरण
$f: N \rightarrow N, f(x) = 5x$ इंजेक्शन है।
$f: N \rightarrow N, f(x) = x^2$ इंजेक्शन है।
$f: R\rightarrow R, f(x) = x^2$ के रूप में इंजेक्शन नहीं है $(-x)^2 = x^2$
विशेषण / ओटो फ़ंक्शन
एक समारोह $f: A \rightarrow B$अगर सर् की छवि इसकी सीमा के बराबर है, तो यह (विशेष) है। समान रूप से, हर के लिए$b \in B$, कुछ मौजूद है $a \in A$ ऐसा है कि $f(a) = b$। इसका अर्थ है कि B में किसी भी y के लिए, A में कुछ x मौजूद है$y = f(x)$।
उदाहरण
$f : N \rightarrow N, f(x) = x + 2$ विशेषण है।
$f : R \rightarrow R, f(x) = x^2$ चूंकि हम एक वास्तविक संख्या नहीं खोज सकते हैं जिसका वर्ग ऋणात्मक है।
विशेषण / एक-से-एक संवाददाता
एक समारोह $f: A \rightarrow B$ यदि केवल और यदि है तो विशेषण या वन-टू-वन संवाददाता है f दोनों इंजेक्शन और विशेषण है।
मुसीबत
साबित करें कि एक फ़ंक्शन $f: R \rightarrow R$ द्वारा परिभाषित $f(x) = 2x – 3$ एक विशेषण फ़ंक्शन है।
Explanation - हमें यह साबित करना होगा कि यह फ़ंक्शन इंजेक्टिव और सर्जेक्टिव दोनों है।
अगर $f(x_1) = f(x_2)$, फिर $2x_1 – 3 = 2x_2 – 3 $ और इसका मतलब है कि $x_1 = x_2$।
इसलिए, एफ है injective।
यहाँ, $2x – 3= y$
इसलिए, $x = (y+5)/3$ जिसका संबंध R और से है $f(x) = y$।
इसलिए, एफ है surjective।
जबसे f दोनों है surjective तथा injective, हम कह सकते हैं f है bijective।
एक फंक्शन का विलोम
inverse एक-के-एक-एक इसी कार्य $f : A \rightarrow B$समारोह है $g : B \rightarrow A$, निम्नलिखित संपत्ति पकड़े -
$f(x) = y \Leftrightarrow g(y) = x$
फ़ंक्शन च को कहा जाता है invertible, अगर इसका उलटा फ़ंक्शन जी मौजूद है।
उदाहरण
एक समारोह $f : Z \rightarrow Z, f(x)=x+5$, उलटा है क्योंकि इसमें उलटा कार्य है $ g : Z \rightarrow Z, g(x)= x-5$।
एक समारोह $f : Z \rightarrow Z, f(x)=x^2$ क्योंकि यह एक-से-एक नहीं है, अतुलनीय नहीं है $(-x)^2=x^2$।
कार्यों की संरचना
दो कार्य $f: A \rightarrow B$ तथा $g: B \rightarrow C$ एक रचना देने के लिए रचना की जा सकती है $g o f$। यह A से C तक का एक फंक्शन है$(gof)(x) = g(f(x))$
उदाहरण
लश्कर $f(x) = x + 2$ तथा $g(x) = 2x + 1$, खोजें $( f o g)(x)$ तथा $( g o f)(x)$।
उपाय
$(f o g)(x) = f (g(x)) = f(2x + 1) = 2x + 1 + 2 = 2x + 3$
$(g o f)(x) = g (f(x)) = g(x + 2) = 2 (x+2) + 1 = 2x + 5$
इसलिये, $(f o g)(x) \neq (g o f)(x)$
रचना के बारे में कुछ तथ्य
यदि f और g एक-से-एक हैं तो फ़ंक्शन $(g o f)$ एक-से-एक है।
यदि f और g कार्य पर हैं $(g o f)$ पर भी है।
रचना में हमेशा साहचर्य संपत्ति होती है, लेकिन सराहनीय संपत्ति नहीं होती है।
गणितीय तर्क के नियम गणितीय कथनों के तर्क के तरीके निर्दिष्ट करते हैं। ग्रीक दार्शनिक, अरस्तू तार्किक तर्क का अग्रणी था। तार्किक तर्क गणित के कई क्षेत्रों और परिणामस्वरूप कंप्यूटर विज्ञान के लिए सैद्धांतिक आधार प्रदान करता है। कंप्यूटर विज्ञान में इसके कई व्यावहारिक अनुप्रयोग हैं जैसे कंप्यूटिंग मशीन का डिज़ाइन, कृत्रिम बुद्धिमत्ता, प्रोग्रामिंग भाषाओं के लिए डेटा संरचनाओं की परिभाषा आदि।
Propositional Logicउन बयानों से संबंधित है जिनसे सत्य मूल्यों, "सत्य" और "असत्य" को सौंपा जा सकता है। उद्देश्य इन कथनों का व्यक्तिगत या समग्र रूप से विश्लेषण करना है।
प्रीपोजल लॉजिक - परिभाषा
एक प्रस्ताव घोषणात्मक कथनों का एक संग्रह होता है, जिसमें या तो सत्य मान "सत्य" या सत्य मान "असत्य" होता है। एक प्रस्ताव में प्रस्ताव चर और संयोजक होते हैं। हम बड़े अक्षरों (A, B, आदि) द्वारा प्रस्ताव चर को निरूपित करते हैं। संयोजकों को प्रपोजल चर से जोड़ा जाता है।
प्रस्ताव के कुछ उदाहरण नीचे दिए गए हैं -
- "मनुष्य नश्वर है", यह सत्य मूल्य "TRUE" लौटाता है
- "12 + 9 = 3 - 2", यह सत्य मूल्य "FALSE" लौटाता है
निम्नलिखित एक प्रस्ताव नहीं है -
"2 से कम है"। ऐसा इसलिए है क्योंकि जब तक हम A का एक विशिष्ट मूल्य नहीं देते, हम यह नहीं कह सकते कि कथन सही है या गलत।
संयोजियों
प्रपोजल लॉजिक में आमतौर पर हम पाँच संयोजनों का उपयोग करते हैं जो हैं -
या$\lor$)
तथा ($\land$)
नकार / नहीं ($\lnot$)
आरोपण / यदि-तब ($\rightarrow$)
यदि और केवल यदि ($\Leftrightarrow$)।
OR ($\lor$) - दो प्रस्तावों ए और बी के ऑपरेशन (के रूप में लिखा गया है $A \lor B$) सही है अगर कम से कम किसी भी प्रस्ताव का चर A या B सत्य है।
सत्य तालिका इस प्रकार है -
| ए | ख | A ∨ बी |
|---|---|---|
| सच | सच | सच |
| सच | असत्य | सच |
| असत्य | सच | सच |
| असत्य | असत्य | असत्य |
AND ($\land$) - दो प्रस्ताव ए और बी के संचालन (के रूप में लिखा गया है $A \land B$) सत्य है यदि प्रस्तावक चर A और B दोनों सत्य है।
सत्य तालिका इस प्रकार है -
| ए | ख | A ∧ बी |
|---|---|---|
| सच | सच | सच |
| सच | असत्य | असत्य |
| असत्य | सच | असत्य |
| असत्य | असत्य | असत्य |
Negation ($\lnot$) - एक प्रस्ताव (एक के रूप में लिखा) की उपेक्षा $\lnot A$) असत्य होने पर असत्य है और अ के असत्य होने पर सत्य है।
सत्य तालिका इस प्रकार है -
| ए | ¬ ए |
|---|---|
| सच | असत्य |
| असत्य | सच |
Implication / if-then ($\rightarrow$) - एक निहितार्थ $A \rightarrow B$प्रस्ताव है "यदि ए, तो बी"। यदि A सत्य है और B मिथ्या है तो यह मिथ्या है। बाकी मामले सच हैं।
सत्य तालिका इस प्रकार है -
| ए | ख | ए → बी |
|---|---|---|
| सच | सच | सच |
| सच | असत्य | असत्य |
| असत्य | सच | सच |
| असत्य | असत्य | सच |
If and only if ($ \Leftrightarrow $) - $A \Leftrightarrow B$ द्वि-सशर्त तार्किक संयोजी है जो कि p और q समान है, अर्थात दोनों असत्य हैं या दोनों सत्य हैं।
सत्य तालिका इस प्रकार है -
| ए | ख | A ⇔ बी |
|---|---|---|
| सच | सच | सच |
| सच | असत्य | असत्य |
| असत्य | सच | असत्य |
| असत्य | असत्य | सच |
tautologies
एक टॉटोलॉजी एक ऐसा फॉर्मूला है जो अपने प्रपोजल वैरिएबल के हर मूल्य के लिए हमेशा सही होता है।
Example - साबित करो $\lbrack (A \rightarrow B) \land A \rbrack \rightarrow B$ एक टॉटोलॉजी है
सत्य तालिका इस प्रकार है -
| ए | ख | ए → बी | (ए → बी) ∧ ए | [(ए → बी)] ए] → बी |
|---|---|---|---|---|
| सच | सच | सच | सच | सच |
| सच | असत्य | असत्य | असत्य | सच |
| असत्य | सच | सच | असत्य | सच |
| असत्य | असत्य | सच | असत्य | सच |
जैसा कि हम हर मूल्य को देख सकते हैं $\lbrack (A \rightarrow B) \land A \rbrack \rightarrow B$ "ट्रू" है, यह एक तनातनी है।
विरोधाभासों
एक विरोधाभास एक सूत्र है जो अपने प्रस्ताव चर के हर मूल्य के लिए हमेशा गलत होता है।
Example - साबित करो $(A \lor B) \land \lbrack ( \lnot A) \land (\lnot B) \rbrack$ एक विरोधाभास है
सत्य तालिका इस प्रकार है -
| ए | ख | A ∨ बी | ¬ ए | ¬ बी | (∧ A) ∧ () B) | (ए) बी) ∧ [(∨ ए) ¬ (] बी)] |
|---|---|---|---|---|---|---|
| सच | सच | सच | असत्य | असत्य | असत्य | असत्य |
| सच | असत्य | सच | असत्य | सच | असत्य | असत्य |
| असत्य | सच | सच | सच | असत्य | असत्य | असत्य |
| असत्य | असत्य | असत्य | सच | सच | सच | असत्य |
जैसा कि हम हर मूल्य को देख सकते हैं $(A \lor B) \land \lbrack ( \lnot A) \land (\lnot B) \rbrack$ "गलत" है, यह एक विरोधाभास है।
आकस्मिकता
आकस्मिकता एक ऐसा सूत्र है, जिसके प्रस्तावक चर के प्रत्येक मूल्य के लिए कुछ सच्चे और कुछ गलत मूल्य हैं।
Example - साबित करो $(A \lor B) \land (\lnot A)$ एक आकस्मिकता
सत्य तालिका इस प्रकार है -
| ए | ख | A ∨ बी | ¬ ए | (ए) बी) ∧ (∨ ए) |
|---|---|---|---|---|
| सच | सच | सच | असत्य | असत्य |
| सच | असत्य | सच | असत्य | असत्य |
| असत्य | सच | सच | सच | सच |
| असत्य | असत्य | असत्य | सच | असत्य |
जैसा कि हम हर मूल्य को देख सकते हैं $(A \lor B) \land (\lnot A)$ दोनों "सच" और "गलत" है, यह एक आकस्मिकता है।
प्रपोजल इक्विवेलेंस
दो कथन X और Y तार्किक रूप से समतुल्य हैं यदि निम्नलिखित में से कोई भी दो स्थितियाँ हैं -
प्रत्येक कथन की सत्य सारणियों में समान सत्य मूल्य हैं।
द्वि-सशर्त बयान $X \Leftrightarrow Y$ एक टॉटोलॉजी है।
Example - साबित करो $\lnot (A \lor B) and \lbrack (\lnot A) \land (\lnot B) \rbrack$ समतुल्य हैं
1 सेंट विधि द्वारा परीक्षण (मिलान सत्य तालिका)
| ए | ख | A ∨ बी | ∨ (ए ¬ बी) | ¬ ए | ¬ बी | [() ए) ∧ (¬ बी)] |
|---|---|---|---|---|---|---|
| सच | सच | सच | असत्य | असत्य | असत्य | असत्य |
| सच | असत्य | सच | असत्य | असत्य | सच | असत्य |
| असत्य | सच | सच | असत्य | सच | असत्य | असत्य |
| असत्य | असत्य | असत्य | सच | सच | सच | सच |
यहाँ, हम सत्य मूल्यों को देख सकते हैं $\lnot (A \lor B) and \lbrack (\lnot A) \land (\lnot B) \rbrack$ समान हैं, इसलिए कथन समकक्ष हैं।
2 एनडी विधि द्वारा परीक्षण (द्वि-स्थिति)
| ए | ख | ∨ (ए ¬ बी) | [() ए) ∧ (¬ बी)] | [[(ए) बी)] ¬ [() ए) ¬ () बी)] |
|---|---|---|---|---|
| सच | सच | असत्य | असत्य | सच |
| सच | असत्य | असत्य | असत्य | सच |
| असत्य | सच | असत्य | असत्य | सच |
| असत्य | असत्य | सच | सच | सच |
जैसा $\lbrack \lnot (A \lor B) \rbrack \Leftrightarrow \lbrack (\lnot A ) \land (\lnot B) \rbrack$ एक tautology है, कथन समकक्ष हैं।
उलटा, बातचीत, और कॉन्ट्रा पॉजिटिव
आरोपण / अगर-तब $(\rightarrow)$को सशर्त विवरण भी कहा जाता है। इसके दो भाग हैं -
- परिकल्पना, पी
- निष्कर्ष, क्ष
जैसा कि पहले उल्लेख किया गया है, यह के रूप में चिह्नित है $p \rightarrow q$।
Example of Conditional Statement- "यदि आप अपना होमवर्क करते हैं, तो आपको दंडित नहीं किया जाएगा।" यहां, "आप अपना होमवर्क करते हैं" परिकल्पना, पी है, और "आपको दंडित नहीं किया जाएगा" निष्कर्ष है, क्ष।
Inverse- सशर्त कथन का विलोम परिकल्पना और निष्कर्ष दोनों का निषेध है। यदि कथन "यदि p है, तो q", व्युत्क्रम "यदि p नहीं है, तो q नहीं"। इस प्रकार का उलटा$p \rightarrow q$ है $ \lnot p \rightarrow \lnot q$।
Example - "यदि आप अपना होमवर्क करते हैं, तो आपको दंडित नहीं किया जाएगा" का विलोम है, "यदि आप अपना होमवर्क नहीं करते हैं, तो आपको दंडित किया जाएगा।"
Converse- सशर्त कथन की व्याख्या परिकल्पना और निष्कर्ष को परस्पर जोड़कर की जाती है। यदि कथन "यदि p है, तो q" है, तो प्रतिफल "If q, तब p" होगा। का कांसेप्ट$p \rightarrow q$ है $q \rightarrow p$।
Example - "यदि आप अपना होमवर्क करते हैं, तो आपको दंडित नहीं किया जाएगा", "यदि आपको दंडित नहीं किया जाएगा, तो आप अपना होमवर्क करते हैं"।
Contra-positive- सशर्त के गर्भ-धनात्मक की गणना परिकल्पना और प्रतिलोम कथन के समापन से की जाती है। यदि कथन "यदि p, तो q" है, तो गर्भनिरोधक सकारात्मक होगा "यदि q नहीं है, तो p नहीं"। का पॉजिटिव-पॉजिटिव$p \rightarrow q$ है $\lnot q \rightarrow \lnot p$।
Example - "यदि आप अपना गृहकार्य करते हैं, तो आपको दंडित नहीं किया जाएगा", "यदि आपको दंडित किया जाता है, तो आपने अपना गृहकार्य नहीं किया है"।
द्वैत तत्त्व
द्वैत सिद्धांत कहता है कि किसी भी सच्चे कथन के लिए, यूनियनों को चौराहों (और इसके विपरीत) में बदलकर और यूनिवर्सल सेट को नल सेट (और इसके विपरीत) में बदलकर प्राप्त किया गया दोहरा बयान भी सत्य है। यदि किसी कथन का दोहराव ही कथन है, तो यह कहा जाता हैself-dual बयान।
Example - का दोहरी $(A \cap B ) \cup C$ है $(A \cup B) \cap C$
सामान्य रूप
हम किसी भी प्रस्ताव को दो सामान्य रूपों में बदल सकते हैं -
- संयोजी सामान्य रूप
- विघटनकारी सामान्य रूप
संयोजक सामान्य रूप
एक यौगिक कथन संयुग्मक सामान्य रूप में होता है यदि इसे ORS के साथ जुड़ा हुआ और चर (शामिल किए गए चरों की उपेक्षा) के बीच प्राप्त किया जाता है। सेट ऑपरेशंस के संदर्भ में, यह यूनियनों से जुड़े चरों के बीच इंटरसेक्शन द्वारा प्राप्त एक यौगिक स्टेटमेंट है।
Examples
$(A \lor B) \land (A \lor C) \land (B \lor C \lor D)$
$(P \cup Q) \cap (Q \cup R)$
विघटनकारी सामान्य रूप
एक कंपाउंड स्टेटमेंट डिसेंटिव नॉर्मल फॉर्म में होता है, अगर इसे ANDs से जुड़े हुए वेरिएबल या वैरिएबल (वैरिएबल को शामिल किया गया) के बीच ऑपरेट करके प्राप्त किया जाता है। सेट ऑपरेशन के संदर्भ में, यह संघ द्वारा प्राप्त चर के बीच एक मिश्रित विवरण है, जो अंतर्क्रियाओं से जुड़ा हुआ है।
Examples
$(A \land B) \lor (A \land C) \lor (B \land C \land D)$
$(P \cap Q) \cup (Q \cap R)$
Predicate Logic विधेय के साथ सौदे, जो चर वाले प्रस्ताव हैं।
विधेय तर्क - परिभाषा
एक विधेय कुछ विशिष्ट डोमेन पर परिभाषित एक या एक से अधिक चर की अभिव्यक्ति है। चर के साथ एक विधेय को चर के लिए एक मान निर्दिष्ट करके या चर की मात्रा निर्धारित करके एक प्रस्ताव बनाया जा सकता है।
निम्नलिखित कुछ उदाहरण हैं -
- E (x, y) को "x = y" निरूपित करें
- एक्स (ए, बी, सी) को "a + b + c = 0" बताएं
- M (x, y) को सूचित करें "x का विवाह y से हुआ है"
अच्छी तरह से तैयार फॉर्मूला
अच्छी तरह से तैयार फॉर्मूला (wff) निम्नलिखित में से किसी को धारण करने वाला एक विधेय है -
सभी प्रस्ताव स्थिरांक और प्रपोजल चर wffs हैं
यदि x एक चर है और Y एक wff है, $\forall x Y$ तथा $\exists x Y$ भी wff हैं
सत्य मूल्य और झूठे मूल्य wffs हैं
प्रत्येक परमाणु सूत्र एक wff है
Wffs को जोड़ने वाले सभी संयोजक wffs हैं
परिमाणकों
प्रेडिसेट्स का चर क्वांटिफायर द्वारा निर्धारित किया जाता है। विधेय तर्क में दो प्रकार के क्वांटिफायर हैं- यूनिवर्सल क्वांटिफायर और एक्स्टिशियनल क्वांटिफायर।
यूनिवर्सल क्वांटिफायर
यूनिवर्सल क्वांटिफायर बताता है कि इसके दायरे में दिए गए कथन विशिष्ट चर के हर मूल्य के लिए सही हैं। इसे प्रतीक द्वारा निरूपित किया जाता है$\forall$।
$\forall x P(x)$ x के हर मान के लिए पढ़ा जाता है, P (x) सत्य है।
Example - "मनुष्य नश्वर है" को प्रस्तावक रूप में बदला जा सकता है $\forall x P(x)$ जहाँ P (x) विधेय है जो x को नश्वर बताता है और प्रवचन का ब्रह्मांड सभी पुरुष हैं।
अस्तित्व मात्रात्मक
अस्तित्ववादी क्वांटिफायर बताता है कि विशिष्ट दायरे के कुछ मूल्यों के लिए इसके दायरे के कथन सही हैं। इसे प्रतीक द्वारा निरूपित किया जाता है$\exists $।
$\exists x P(x)$ x के कुछ मानों के रूप में पढ़ा जाता है, P (x) सत्य है।
Example - "कुछ लोग बेईमान होते हैं" को प्रपोजल के रूप में बदला जा सकता है $\exists x P(x)$ जहाँ P (x) विधेय है जो x को निरर्थक बताता है और प्रवचन का ब्रह्मांड कुछ लोग हैं।
नेस्टेड क्वांटिफायर
यदि हम किसी ऐसे क्वांटिफायर का उपयोग करते हैं जो किसी अन्य क्वांटिफायर के दायरे में आता है, तो इसे नेस्टेड क्वांटिफायर कहा जाता है।
Example
$\forall\ a\: \exists b\: P (x, y)$ कहाँ पे $P (a, b)$ अर्थ है $a + b = 0$
$\forall\ a\: \forall\: b\: \forall\: c\: P (a, b, c)$ कहाँ पे $P (a, b)$ अर्थ है $a + (b + c) = (a + b) + c$
Note - $\forall\: a\: \exists b\: P (x, y) \ne \exists a\: \forall b\: P (x, y)$
उन बयानों से नए बयानों को हटाने के लिए जिनकी सच्चाई हम पहले से जानते हैं, Rules of Inference उपयोग किया जाता है।
के लिए नियम क्या हैं?
गणितीय तर्क अक्सर तार्किक प्रमाण के लिए उपयोग किया जाता है। प्रमाण वैध तर्क हैं जो गणितीय कथनों के सत्य मूल्यों को निर्धारित करते हैं।
एक तर्क बयानों का एक क्रम है। अंतिम कथन निष्कर्ष है और इसके सभी पूर्ववर्ती बयानों को परिसर (या परिकल्पना) कहा जाता है। प्रतीक "$\therefore$", (इसलिए पढ़ें) निष्कर्ष से पहले रखा गया है। एक वैध तर्क वह है जहां निष्कर्ष परिसर के सत्य मूल्यों से होता है।
आक्षेप के नियम हमारे पास पहले से मौजूद बयानों से मान्य तर्क के निर्माण के लिए टेम्पलेट या दिशानिर्देश प्रदान करते हैं।
नियमों की तालिका
| नियम का पालन | नाम | नियम का पालन | नाम |
|---|---|---|---|
$$\begin{matrix} P \\ \hline \therefore P \lor Q \end{matrix}$$ |
इसके अलावा |
$$\begin{matrix} P \lor Q \\ \lnot P \\ \hline \therefore Q \end{matrix}$$ |
विवादास्पद सिलोलवाद |
$$\begin{matrix} P \\ Q \\ \hline \therefore P \land Q \end{matrix}$$ |
संयोजन के रूप |
$$\begin{matrix} P \rightarrow Q \\ Q \rightarrow R \\ \hline \therefore P \rightarrow R \end{matrix}$$ |
हाइपोथेटिकल सिलियोलिज़म |
$$\begin{matrix} P \land Q\\ \hline \therefore P \end{matrix}$$ |
सरलीकरण |
$$\begin{matrix} ( P \rightarrow Q ) \land (R \rightarrow S) \\ P \lor R \\ \hline \therefore Q \lor S \end{matrix}$$ |
रचनात्मक दुविधा |
$$\begin{matrix} P \rightarrow Q \\ P \\ \hline \therefore Q \end{matrix}$$ |
एक वैध, सरल तर्क और निष्कर्ष के नियम के रूप |
$$\begin{matrix} (P \rightarrow Q) \land (R \rightarrow S) \\ \lnot Q \lor \lnot S \\ \hline \therefore \lnot P \lor \lnot R \end{matrix}$$ |
विनाशकारी दुविधा |
$$\begin{matrix} P \rightarrow Q \\ \lnot Q \\ \hline \therefore \lnot P \end{matrix}$$ |
मोडस टोलेंस |
इसके अलावा
यदि P एक आधार है, तो हम व्युत्पन्न नियम का उपयोग कर सकते हैं $ P \lor Q $।
$$\begin{matrix} P \\ \hline \therefore P \lor Q \end{matrix}$$
Example
Let P be the proposition, “He studies very hard” is true
Therefore − "Either he studies very hard Or he is a very bad student." Here Q is the proposition “he is a very bad student”.
Conjunction
If P and Q are two premises, we can use Conjunction rule to derive $ P \land Q $.
$$\begin{matrix} P \\ Q \\ \hline \therefore P \land Q \end{matrix}$$
Example
Let P − “He studies very hard”
Let Q − “He is the best boy in the class”
Therefore − "He studies very hard and he is the best boy in the class"
Simplification
If $P \land Q$ is a premise, we can use Simplification rule to derive P.
$$\begin{matrix} P \land Q\\ \hline \therefore P \end{matrix}$$
Example
"He studies very hard and he is the best boy in the class", $P \land Q$
Therefore − "He studies very hard"
Modus Ponens
If P and $P \rightarrow Q$ are two premises, we can use Modus Ponens to derive Q.
$$\begin{matrix} P \rightarrow Q \\ P \\ \hline \therefore Q \end{matrix}$$
Example
"If you have a password, then you can log on to facebook", $P \rightarrow Q$
"You have a password", P
Therefore − "You can log on to facebook"
Modus Tollens
If $P \rightarrow Q$ and $\lnot Q$ are two premises, we can use Modus Tollens to derive $\lnot P$.
$$\begin{matrix} P \rightarrow Q \\ \lnot Q \\ \hline \therefore \lnot P \end{matrix}$$
Example
"If you have a password, then you can log on to facebook", $P \rightarrow Q$
"You cannot log on to facebook", $\lnot Q$
Therefore − "You do not have a password "
Disjunctive Syllogism
If $\lnot P$ and $P \lor Q$ are two premises, we can use Disjunctive Syllogism to derive Q.
$$\begin{matrix} \lnot P \\ P \lor Q \\ \hline \therefore Q \end{matrix}$$
Example
"The ice cream is not vanilla flavored", $\lnot P$
"The ice cream is either vanilla flavored or chocolate flavored", $P \lor Q$
Therefore − "The ice cream is chocolate flavored”
Hypothetical Syllogism
If $P \rightarrow Q$ and $Q \rightarrow R$ are two premises, we can use Hypothetical Syllogism to derive $P \rightarrow R$
$$\begin{matrix} P \rightarrow Q \\ Q \rightarrow R \\ \hline \therefore P \rightarrow R \end{matrix}$$
Example
"If it rains, I shall not go to school”, $P \rightarrow Q$
"If I don't go to school, I won't need to do homework", $Q \rightarrow R$
Therefore − "If it rains, I won't need to do homework"
Constructive Dilemma
If $( P \rightarrow Q ) \land (R \rightarrow S)$ and $P \lor R$ are two premises, we can use constructive dilemma to derive $Q \lor S$.
$$\begin{matrix} ( P \rightarrow Q ) \land (R \rightarrow S) \\ P \lor R \\ \hline \therefore Q \lor S \end{matrix}$$
Example
“If it rains, I will take a leave”, $( P \rightarrow Q )$
“If it is hot outside, I will go for a shower”, $(R \rightarrow S)$
“Either it will rain or it is hot outside”, $P \lor R$
Therefore − "I will take a leave or I will go for a shower"
Destructive Dilemma
If $(P \rightarrow Q) \land (R \rightarrow S)$ and $ \lnot Q \lor \lnot S $ are two premises, we can use destructive dilemma to derive $\lnot P \lor \lnot R$.
$$\begin{matrix} (P \rightarrow Q) \land (R \rightarrow S) \\ \lnot Q \lor \lnot S \\ \hline \therefore \lnot P \lor \lnot R \end{matrix}$$
Example
“If it rains, I will take a leave”, $(P \rightarrow Q )$
“If it is hot outside, I will go for a shower”, $(R \rightarrow S)$
“Either I will not take a leave or I will not go for a shower”, $\lnot Q \lor \lnot S$
Therefore − "Either it does not rain or it is not hot outside"
Group Theory is a branch of mathematics and abstract algebra that defines an algebraic structure named as group. Generally, a group comprises of a set of elements and an operation over any two elements on that set to form a third element also in that set.
In 1854, Arthur Cayley, the British Mathematician, gave the modern definition of group for the first time −
“A set of symbols all of them different, and such that the product of any two of them (no matter in what order), or the product of any one of them into itself, belongs to the set, is said to be a group. These symbols are not in general convertible [commutative], but are associative.”
In this chapter, we will know about operators and postulates that form the basics of set theory, group theory and Boolean algebra.
Any set of elements in a mathematical system may be defined with a set of operators and a number of postulates.
A binary operator defined on a set of elements is a rule that assigns to each pair of elements a unique element from that set. For example, given the set $ A = \lbrace 1, 2, 3, 4, 5 \rbrace $, we can say $\otimes$ is a binary operator for the operation $c = a \otimes b$, if it specifies a rule for finding c for the pair of $(a,b)$, such that $a,b,c \in A$.
The postulates of a mathematical system form the basic assumptions from which rules can be deduced. The postulates are −
Closure
A set is closed with respect to a binary operator if for every pair of elements in the set, the operator finds a unique element from that set.
Example
Let $A = \lbrace 0, 1, 2, 3, 4, 5, \dots \rbrace$
This set is closed under binary operator into $(\ast)$, because for the operation $c = a \ast b$, for any $a, b \in A$, the product $c \in A$.
The set is not closed under binary operator divide $(\div)$, because, for the operation $c = a \div b$, for any $a, b \in A$, the product c may not be in the set A. If $a = 7, b = 2$, then $c = 3.5$. Here $a,b \in A$ but $c \notin A$.
Associative Laws
A binary operator $\otimes$ on a set A is associative when it holds the following property −
$(x \otimes y) \otimes z = x \otimes (y \otimes z)$, where $x, y, z \in A $
Example
Let $A = \lbrace 1, 2, 3, 4 \rbrace$
The operator plus $( + )$ is associative because for any three elements, $x,y,z \in A$, the property $(x + y) + z = x + ( y + z )$ holds.
The operator minus $( - )$ is not associative since
$$( x - y ) - z \ne x - ( y - z )$$
Commutative Laws
A binary operator $\otimes$ on a set A is commutative when it holds the following property −
$x \otimes y = y \otimes x$, कहाँ पे $x, y \in A$
उदाहरण
लश्कर $A = \lbrace 1, 2, 3, 4 \rbrace$
ऑपरेटर प्लस $( + )$ क्योंकि किसी भी दो तत्वों के लिए सराहनीय है, $x,y \in A$, संपत्ति $x + y = y + x$ आयोजित करता है।
ऑपरेटर माइनस $( - )$ तब से सहयोगी नहीं है
$$x - y \ne y - x$$
वितरण संबंधी कानून
दो बाइनरी ऑपरेटर $\otimes$ तथा $\circledast$ एक सेट ए पर, ऑपरेटर पर वितरण कर रहे हैं $\circledast$ जब निम्नलिखित संपत्ति रखती है -
$x \otimes (y \circledast z) = (x \otimes y) \circledast (x \otimes z)$, कहाँ पे $x, y, z \in A $
उदाहरण
लश्कर $A = \lbrace 1, 2, 3, 4 \rbrace$
ऑपरेटरों में $( * )$ और प्लस $( + )$ ऑपरेटर पर वितरण कर रहे हैं + क्योंकि किसी भी तीन तत्वों के लिए, $x,y,z \in A$, संपत्ति $x * ( y + z ) = ( x * y ) + ( x * z )$ आयोजित करता है।
हालांकि, ये ऑपरेटर अधिक वितरण नहीं कर रहे हैं $*$ जबसे
$$x + ( y * z ) \ne ( x + y ) * ( x + z )$$
पहचान तत्व
बाइनरी ऑपरेशन के संबंध में एक सेट ए में एक पहचान तत्व होता है $\otimes$ A पर, यदि कोई तत्व मौजूद है $e \in A$, जैसे कि निम्नलिखित संपत्ति रखती है -
$e \otimes x = x \otimes e$, कहाँ पे $x \in A$
उदाहरण
लश्कर $Z = \lbrace 0, 1, 2, 3, 4, 5, \dots \rbrace$
तत्व 1 ऑपरेशन के संबंध में एक पहचान तत्व है $*$ किसी भी तत्व के लिए $x \in Z$,
$$1 * x = x * 1$$
दूसरी ओर, ऑपरेशन माइनस के लिए कोई पहचान तत्व नहीं है $( - )$
श्लोक में
यदि एक सेट A में एक पहचान तत्व है $e$ एक बाइनरी ऑपरेटर के संबंध में $\otimes $, यह कहा जाता है कि हर तत्व के लिए जब भी एक व्युत्क्रम होता है $x \in A$, वहाँ एक और तत्व मौजूद है $y \in A$, जैसे कि निम्नलिखित संपत्ति रखती है -
$$x \otimes y = e$$
उदाहरण
लश्कर $A = \lbrace \dots -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, \dots \rbrace$
ऑपरेशन प्लस दिया $( + )$ तथा $e = 0$, किसी भी तत्व x का विलोम है $(-x)$ जबसे $x + (x) = 0$
डी मॉर्गन का नियम
डी मॉर्गन के कानून संघों और उनकी बस्तियों के संदर्भ में दो (या अधिक) सेट के चौराहे के बीच परिवर्तन की एक जोड़ी देते हैं। कानून हैं -
$$(A \cup B)' = A' \cap B'$$
$$(A \cap B)' = A' \cup B'$$
उदाहरण
लश्कर $A = \lbrace 1, 2, 3, 4 \rbrace ,B = \lbrace 1, 3, 5, 7 \rbrace$, तथा
सार्वसमुच्चय $U = \lbrace 1, 2, 3, \dots, 9, 10 \rbrace$
$A' = \lbrace 5, 6, 7, 8, 9, 10 \rbrace$
$B' = \lbrace 2, 4, 6, 8, 9, 10 \rbrace$
$A \cup B = \lbrace 1, 2, 3, 4, 5, 7 \rbrace$
$A \cap B = \lbrace 1, 3 \rbrace $
$(A \cup B)' = \lbrace 6, 8, 9, 10 \rbrace$
$A' \cap B' = \lbrace 6, 8, 9, 10 \rbrace$
इस प्रकार, हम देखते हैं कि $(A \cup B)' = A' \cap B'$
$(A \cap B)' = \lbrace 2, 4, 5, 6, 7, 8, 9, 10 \rbrace$
$A' \cup B' = \lbrace 2, 4, 5, 6, 7, 8, 9, 10 \rbrace$
इस प्रकार, हम देखते हैं कि $(A \cap B)' = A' \cup B'$
semigroup
एक परिमित या अनंत समुच्चय $‘S’$ एक बाइनरी ऑपरेशन के साथ $‘\omicron’$ (संरचना) को अर्धसमूह कहा जाता है यदि यह एक साथ दो शर्तों का पालन करता है -
Closure - हर जोड़ी के लिए $(a, b) \in S, \:(a \omicron b)$ सेट में उपस्थित होना होगा $S$।
Associative - हर तत्व के लिए $a, b, c \in S, (a \omicron b) \omicron c = a \omicron (b \omicron c)$ अवश्य होल्ड करें।
उदाहरण
अतिरिक्त ऑपरेशन के साथ सकारात्मक पूर्णांक (शून्य को छोड़कर) का सेट एक अर्धवृत्त है। उदाहरण के लिए,$ S = \lbrace 1, 2, 3, \dots \rbrace $
यहाँ क्लोजर प्रॉपर्टी हर जोड़े के लिए है $(a, b) \in S, (a + b)$ उदाहरण के लिए सेट एस में मौजूद है, $1 + 2 = 3 \in S]$
साहचर्य संपत्ति भी प्रत्येक तत्व के लिए रखती है $a, b, c \in S, (a + b) + c = a + (b + c)$। उदाहरण के लिए,$(1 + 2) + 3 = 1 + (2 + 3) = 5$
monoid
एक पहचान तत्व के साथ एक अर्धवृत्त है। पहचान तत्व (द्वारा चिह्नित)$e$ या E) एक सेट S का एक ऐसा तत्व है $(a \omicron e) = a$हर तत्व के लिए $a \in S$। एक पहचान तत्व भी कहा जाता हैunit element। तो, एक मोनोड एक साथ तीन गुण रखता है -Closure, Associative, Identity element।
उदाहरण
गुणन ऑपरेशन के साथ धनात्मक पूर्णांक (शून्य को छोड़कर) का सेट एक मोनॉयड है। $S = \lbrace 1, 2, 3, \dots \rbrace $
यहाँ क्लोजर प्रॉपर्टी हर जोड़े के लिए है $(a, b) \in S, (a \times b)$ सेट एस में मौजूद है [उदाहरण के लिए, $1 \times 2 = 2 \in S$ और इसी तरह]
साहचर्य संपत्ति भी प्रत्येक तत्व के लिए रखती है $a, b, c \in S, (a \times b) \times c = a \times (b \times c)$ [उदाहरण के लिए, $(1 \times 2) \times 3 = 1 \times (2 \times 3) = 6$ और इसी तरह]
पहचान संपत्ति भी प्रत्येक तत्व के लिए रखती है $a \in S, (a \times e) = a$ [उदाहरण के लिए, $(2 \times 1) = 2, (3 \times 1) = 3$और इसी तरह]। यहां पहचान तत्व 1 है।
समूह
एक समूह एक उलटा तत्व वाला एक मोनॉयड है। सेट S का व्युत्क्रम तत्व (I द्वारा निरूपित) एक ऐसा तत्व है$(a \omicron I) = (I \omicron a) = a$प्रत्येक तत्व के लिए $a \in S$। तो, एक समूह चार गुण एक साथ रखता है - i) बंद करना, ii) साहचर्य, iii) पहचान तत्व, iv) उलटा तत्व। एक समूह G का क्रम G में तत्वों की संख्या है और एक समूह में एक तत्व का क्रम सबसे कम सकारात्मक पूर्णांक n है जो कि उस समूह G का पहचान तत्व है।
उदाहरण
का समूह $N \times N$ गैर-एकवचन मैट्रिक्स मैट्रिक्स गुणन ऑपरेशन के तहत एक समूह बनाते हैं।
दो का उत्पाद $N \times N$ गैर-एकवचन मैट्रिक्स भी एक है $N \times N$ गैर-विलक्षण मैट्रिक्स जो क्लोजर गुण रखता है।
मैट्रिक्स गुणन ही सहयोगी है। इसलिए, साहचर्य संपत्ति रखती है।
का समूह $N \times N$ गैर-एकवचन मैट्रिक्स में पहचान तत्व की संपत्ति को पहचानने वाले मैट्रिक्स होते हैं।
जैसा कि सभी मैट्रीस गैर-विलक्षण होते हैं, उन सभी में विलोम तत्व होते हैं जो कि नॉनसिंगुलर मैट्रिस भी होते हैं। इसलिए, व्युत्क्रम संपत्ति भी रखती है।
एबेलियन ग्रुप
एबेलियन समूह जी एक समूह है जिसके लिए तत्व जोड़ी है $(a,b) \in G$हमेशा सराहनीय कानून रखता है। तो, एक समूह पाँच गुणों को एक साथ रखता है - i) बंद करना, ii) सहयोगी, iii) पहचान तत्व, iv) उलटा तत्व, v) कम्यूटेटिव।
उदाहरण
अतिरिक्त संचालन के साथ सकारात्मक पूर्णांक (शून्य सहित) का सेट एक एबेलियन समूह है। $G = \lbrace 0, 1, 2, 3, \dots \rbrace$
यहाँ क्लोजर प्रॉपर्टी हर जोड़े के लिए है $(a, b) \in S, (a + b)$ सेट एस में मौजूद है [उदाहरण के लिए, $1 + 2 = 2 \in S$ और इसी तरह]
साहचर्य संपत्ति भी प्रत्येक तत्व के लिए रखती है $a, b, c \in S, (a + b) + c = a + (b + c)$ [उदाहरण के लिए, $(1 +2) + 3 = 1 + (2 + 3) = 6$ और इसी तरह]
पहचान संपत्ति भी प्रत्येक तत्व के लिए रखती है $a \in S, (a \times e) = a$ [उदाहरण के लिए, $(2 \times 1) = 2, (3 \times 1) = 3$और इसी तरह]। यहाँ, पहचान तत्व 1 है।
कम्यूटेटिव प्रॉपर्टी भी हर तत्व के लिए है $a \in S, (a \times b) = (b \times a)$ [उदाहरण के लिए, $(2 \times 3) = (3 \times 2) = 3$ और इसी तरह]
चक्रीय समूह और उपसमूह
ए cyclic groupएक समूह है जो एक एकल तत्व द्वारा उत्पन्न किया जा सकता है। चक्रीय समूह का प्रत्येक तत्व किसी विशिष्ट तत्व की एक शक्ति है जिसे जनरेटर कहा जाता है। एक जनरेटर समूह को 'g' द्वारा उत्पन्न किया जा सकता है, जैसे कि समूह के हर दूसरे तत्व को जनरेटर 'g' की शक्ति के रूप में लिखा जा सकता है।
उदाहरण
जटिल संख्याओं का समूह $\lbrace 1,-1, i, -i \rbrace$ गुणा ऑपरेशन के तहत एक चक्रीय समूह है।
दो जनरेटर हैं - $i$ तथा $–i$ जैसा $i^1 = i, i^2 = -1, i^3 = -i, i^4 = 1$ और भी $(–i)^1 = -i, (–i)^2 = -1, (–i)^3 = i, (–i)^4 = 1$जो समूह के सभी तत्वों को कवर करता है। इसलिए, यह एक चक्रीय समूह है।
Note - ए cyclic groupहमेशा एक एबेलियन समूह होता है, लेकिन हर एबेलियन समूह एक चक्रीय समूह नहीं होता है। इसके अलावा तर्कसंगत संख्याएं चक्रीय नहीं हैं, लेकिन एबिलियन हैं।
ए subgroup H एक समूह G का एक उपसमूह है (इसके द्वारा निरूपित) $H ≤ G$) यदि यह एक साथ चार गुणों को संतुष्ट करता है - Closure, Associative, Identity element, तथा Inverse।
एक समूह G का एक उपसमूह H जिसमें पूरा समूह G शामिल नहीं है, एक उचित उपसमूह कहा जाता है (Denoted by) $H < G$)। चक्रीय समूह का एक उपसमूह चक्रीय होता है और एक अबेलियन उपसमूह भी अबेलियन होता है।
उदाहरण
एक समूह दें $G = \lbrace 1, i, -1, -i \rbrace$
फिर कुछ उपसमूह हैं $H_1 = \lbrace 1 \rbrace, H_2 = \lbrace 1,-1 \rbrace$,
यह उपसमूह नहीं है - $H_3 = \lbrace 1, i \rbrace$ क्योंकि वह $(i)^{-1} = -i$ इसमें नहीं है $H_3$
आंशिक रूप से ऑर्डर किया गया सेट (POSET)
एक आंशिक रूप से आदेशित सेट में एक द्विआधारी संबंध के साथ एक सेट होता है जो रिफ्लेक्सिव, एंटीसिमेट्रिक और ट्रांसेटिव होता है। "आंशिक रूप से आदेशित सेट" को POSET के रूप में संक्षिप्त किया गया है।
उदाहरण
बाइनरी ऑपरेशन के तहत वास्तविक संख्याओं का सेट, जिसके बराबर या उससे कम है $(\le)$ एक स्थिति है।
सेट होने दो $S = \lbrace 1, 2, 3 \rbrace$ और ऑपरेशन है $\le$
संबंध होंगे $\lbrace(1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3)\rbrace$
यह संबंध R जैसा ही प्रतिवर्ती है $\lbrace (1, 1), (2, 2), (3, 3)\rbrace \in R$
यह संबंध आर सममिति है, जैसा कि
$\lbrace (1, 2), (1, 3), (2, 3) \rbrace \in R\ and\ \lbrace (1, 2), (1, 3), (2, 3) \rbrace ∉ R$
यह संबंध R भी जैसा है $\lbrace (1,2), (2,3), (1,3)\rbrace \in R$।
इसलिए, यह एक है poset।
ऑपरेशन 'रीचैबिलिटी' के तहत एक निर्देशित चक्रीय ग्राफ का शीर्ष सेट एक पोसैट है।
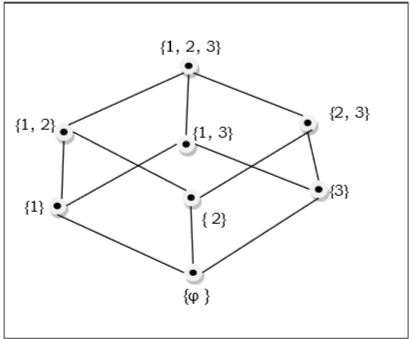
हेस आरेख
एक पोज़ेट का हेज़ आरेख एक निर्देशित ग्राफ़ होता है जिसका वर्टिकल उस पॉज़ेट का तत्व होता है और आर्क्स पोज़ में जोड़े (x, y) को कवर करता है। अगर पोज़ में$x < y$, तब बिंदु x हस आरेख में बिंदु y से कम दिखाई देता है। अगर$x<y<z$ पॉसेट में, तब तीर को x और z के बीच नहीं दिखाया गया है क्योंकि यह निहित है।
उदाहरण
के सबसेट की स्थिति $\lbrace 1, 2, 3 \rbrace = \lbrace \emptyset, \lbrace 1 \rbrace, \lbrace 2 \rbrace, \lbrace 3 \rbrace, \lbrace 1, 2 \rbrace, \lbrace 1, 3 \rbrace, \lbrace 2, 3 \rbrace, \lbrace 1, 2, 3 \rbrace \rbrace$ निम्नलिखित हसी चित्र द्वारा दिखाया गया है -
रैखिक आदेशित सेट
रेखीय रूप से ऑर्डर किया गया सेट या कुल ऑर्डर किया गया सेट एक आंशिक ऑर्डर सेट है जिसमें तत्व की प्रत्येक जोड़ी तुलनीय है। अवयव$a, b \in S$ कहा जाता है कि यदि तुलनात्मक हो तो $a \le b$ या $b \le a$आयोजित करता है। ट्राइकोटॉमी कानून इस कुल निर्धारित सेट को परिभाषित करता है। एक पूरी तरह से आदेशित सेट को संपत्ति के वितरण वाले जाली के रूप में परिभाषित किया जा सकता है$\lbrace a \lor b, a \land b \rbrace = \lbrace a, b \rbrace$ सेट एस में ए और बी के सभी मूल्यों के लिए।
उदाहरण
की शक्ति $\lbrace a, b \rbrace$ \ subseteq द्वारा आदेशित एक पूरी तरह से आदेशित शक्ति सेट के सभी तत्व हैं $P = \lbrace \emptyset, \lbrace a \rbrace, \lbrace b \rbrace, \lbrace a, b\rbrace \rbrace$ तुलनीय हैं।
गैर-कुल आदेश सेट का उदाहरण
एक सेट $S = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ ऑपरेशन के तहत x डिवाइसेज y कुल ऑर्डर सेट नहीं है।
यहाँ, सभी के लिए $(x, y) \in S, x | y$पकड़ना है लेकिन यह सच नहीं है 2 | 3, के रूप में 2 विभाजित नहीं करता है 3 या 3 विभाजित नहीं करता है 2. इसलिए, यह कुल आदेशित सेट नहीं है।
जाली
जाली एक पोज है $(L, \le)$ जिसके लिए हर जोड़ी $\lbrace a, b \rbrace \in L$ कम से कम ऊपरी सीमा है (द्वारा चिह्नित) $a \lor b$) और सबसे बड़ी निचली बाउंड (द्वारा चिह्नित) $a \land b$)। एलयूबी$(\lbrace a,b \rbrace)$को a और b का जोड़ कहा जाता है। GLB$(\lbrace a,b \rbrace )$ को a और b का मिलन कहा जाता है।
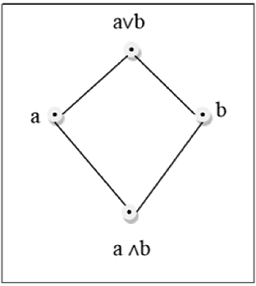
उदाहरण
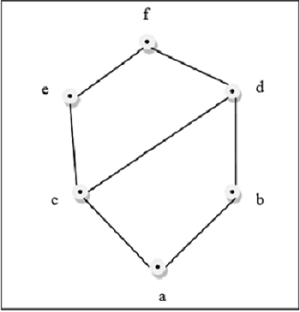
यह उपरोक्त आंकड़ा एक जाली है क्योंकि हर जोड़ी के लिए $\lbrace a, b \rbrace \in L$, एक GLB और एक LUB मौजूद है।
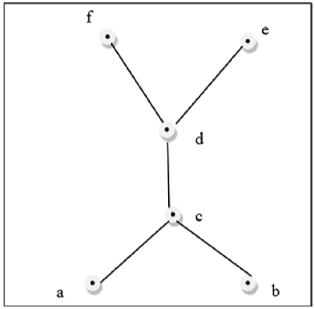
यह उपरोक्त आंकड़ा एक जाली नहीं है क्योंकि $GLB (a, b)$ तथा $LUB (e, f)$ अस्तित्व में नहीं है।
कुछ अन्य अक्षांशों की चर्चा नीचे की गई है -
बंधे हुए जाली
एक जाली L एक बंधी हुई जाली बन जाती है अगर उसमें सबसे बड़ा तत्व 1 और सबसे कम तत्व 0 हो।
लागू किया गया जाली
एक जाली एल एक पूरक जाली बन जाती है यदि यह एक बंधी हुई जाली है और यदि जाली के प्रत्येक तत्व का पूरक है। एक तत्व x में एक पूरक x 'यदि है$\exists x(x \land x’=0 and x \lor x’ = 1)$
वितरण योग्य जाली
यदि एक जाली निम्नलिखित दो वितरण गुणों को संतुष्ट करती है, तो इसे वितरण जाली कहा जाता है।
$a \lor (b \land c) = (a \lor b) \land (a \lor c)$
$a \land (b \lor c) = (a \land b) \lor (a \land c)$
मॉड्यूलर जाली
यदि एक जाली निम्नलिखित संपत्ति को संतुष्ट करती है, तो इसे मॉड्यूलर जाली कहा जाता है।
$a \land( b \lor (a \land d)) = (a \land b) \lor (a \land d)$
लत्ती के गुण
इम्पोटोटेंट गुण
$a \lor a = a$
$a \land a = a$
अवशोषण गुण
$a \lor (a \land b) = a$
$a \land (a \lor b) = a$
कम्यूटेटिव गुण
$a \lor b = b \lor a$
$a \land b = b \land a$
सहयोगी गुण
$a \lor (b \lor c) = (a \lor b) \lor c$
$a \land (b \land c) = (a \land b) \land c$
एक जाली का दोहरी
एक जाली का द्वंद्व 'को आपस में जोड़ने से प्राप्त होता है।$\lor$' तथा '$\land$'संचालन।
उदाहरण
का द्वैत $\lbrack a \lor (b \land c) \rbrack\ is\ \lbrack a \land (b \lor c) \rbrack$
दैनिक जीवन में, कई बार घटनाओं की एक श्रृंखला के लिए सभी संभावित परिणामों की संख्या का पता लगाने की आवश्यकता होती है। उदाहरण के लिए, 50 पुरुषों और 38 महिलाओं में से 6 पुरुषों और 4 महिलाओं वाले न्यायाधीशों के एक पैनल को कितने तरीकों से चुना जा सकता है? कितने अलग-अलग 10 अक्षर वाले पैन नंबर जेनरेट किए जा सकते हैं, जैसे पहले पांच अक्षर कैपिटल अल्फाबेट्स हैं, अगले चार डिजिट हैं और आखिरी में फिर से कैपिटल लेटर है। इन समस्याओं को हल करने के लिए, गिनती के गणितीय सिद्धांत का उपयोग किया जाता है।Counting मुख्य रूप से मौलिक गणना नियम, क्रमपरिवर्तन नियम और संयोजन नियम शामिल हैं।
सम और उत्पाद के नियम
Rule of Sum तथा Rule of Product कठिन समस्याओं को सरल समस्याओं में समाप्त करने के लिए उपयोग किया जाता है।
The Rule of Sum - यदि कार्यों का एक क्रम $T_1, T_2, \dots, T_m$ में किया जा सकता है $w_1, w_2, \dots w_m$ क्रमशः तरीके (शर्त यह है कि कोई भी कार्य एक साथ नहीं किया जा सकता है), फिर इनमें से किसी एक कार्य को करने के तरीकों की संख्या है $w_1 + w_2 + \dots +w_m$। यदि हम दो कार्यों A और B पर विचार करते हैं जो असम्बद्ध हैं (अर्थात$A \cap B = \emptyset$), फिर गणितीय रूप से $|A \cup B| = |A| + |B|$
The Rule of Product - यदि कार्यों का एक क्रम $T_1, T_2, \dots, T_m$ में किया जा सकता है $w_1, w_2, \dots w_m$ पिछले कार्य की घटना के बाद क्रमशः और प्रत्येक कार्य आता है, तब होते हैं $w_1 \times w_2 \times \dots \times w_m$कार्य करने के तरीके। गणितीय रूप से, यदि कोई कार्य B कार्य A के बाद आता है, तो$|A \times B| = |A|\times|B|$
उदाहरण
Question- एक लड़का X पर रहता है और Z पर स्कूल जाना चाहता है। अपने घर से X को पहले Y और फिर Y से Z तक पहुंचना है। वह 3 बस मार्गों या 2 ट्रेन मार्गों से X से Y तक जा सकता है। वहां से, वह या तो Z तक पहुँचने के लिए 4 बस मार्गों या 5 ट्रेन मार्गों को चुन सकता है। X से Z तक जाने के लिए कितने रास्ते हैं?
Solution - X से Y तक, वह अंदर जा सकता है $3 + 2 = 5$तरीके (नियम का योग)। इसके बाद, वह Y से Z में जा सकता है$4 + 5 = 9$तरीके (नियम का योग)। इसलिए X से Z तक वह अंदर जा सकता है$5 \times 9 = 45$ तरीके (उत्पाद का नियम)।
क्रमपरिवर्तन
ए permutationकुछ तत्वों की एक व्यवस्था है जिसमें क्रम मायने रखता है। दूसरे शब्दों में एक क्रमपरिवर्तन तत्वों का एक संयोजित संयोजन है।
उदाहरण
एक सेट S = {x, y, z} से एक समय में दो लेने से, सभी क्रमपरिवर्तन हैं -
$ xy, yx, xz, zx, yz, zy $।
हमें संख्याओं के समूह से तीन अंकों की संख्याओं का क्रमचय तैयार करना होगा $S = \lbrace 1, 2, 3 \rbrace$। जब हम अंकों की व्यवस्था करेंगे तो अलग-अलग तीन अंकों की संख्या बनेगी। क्रमोन्नति = 123, 132, 213, 231, 312, 321 होगी
क्रमपरिवर्तन की संख्या
एक बार में 'आर' द्वारा ली गई 'एन' विभिन्न चीजों के क्रमपरिवर्तन की संख्या को निरूपित किया जाता है $n_{P_{r}}$
$$n_{P_{r}} = \frac{n!}{(n - r)!}$$
कहाँ पे $n! = 1.2.3. \dots (n - 1).n$
Proof - विभिन्न तत्वों को 'एन' होने दें।
पहले स्थान को भरने के लिए कई तरीके हैं। तत्वों के पहले स्थान (n-1) को भरने के बाद छोड़ दिया जाता है। इसलिए, दूसरे स्थान को भरने के लिए (एन -1) तरीके हैं। पहले और दूसरे स्थान को भरने के बाद, (n-2) तत्वों की संख्या शेष है। इसलिए, तीसरे स्थान को भरने के लिए (एन -2) तरीके हैं। अब हम [n - (r-1)] = n-r 1 के रूप में r-th स्थान को भरने के तरीकों की संख्या को सामान्य कर सकते हैं;
तो, कुल सं। पहली जगह से आर-थ-प्लेस तक भरने के तरीके -
$n_{ P_{ r } } = n (n-1) (n-2)..... (n-r + 1)$
$= [n(n-1)(n-2) ... (n-r + 1)] [(n-r)(n-r-1) \dots 3.2.1] / [(n-r)(n-r-1) \dots 3.2.1]$
इसलिये,
$n_{ P_{ r } } = n! / (n-r)!$
क्रमपरिवर्तन के कुछ महत्वपूर्ण सूत्र
अगर वहाँ n तत्व हैं$a_1$ किसी तरह के एक जैसे हैं, $a_2$ दूसरी तरह के हैं; $a_3$ तीसरे तरह के एक जैसे हैं और इतने पर और $a_r$ के हैं $r^{th}$ दयालु, कहाँ $(a_1 + a_2 + ... a_r) = n$।
फिर, इन n ऑब्जेक्ट्स के क्रमपरिवर्तन की संख्या = है $n! / [(a_1!(a_2!) \dots (a_r!)]$।
एक बार में n तत्व लेने वाले n अलग तत्वों के क्रमपरिवर्तन की संख्या = $n_{P_n} = n!$
एक समय में r तत्वों को लेने वाले n असामाजिक तत्वों के क्रमपरिवर्तन की संख्या, जब x विशेष चीजें हमेशा निश्चित स्थानों पर कब्जा करती हैं = $n-x_{p_{r-x}}$
N असमान तत्वों के क्रमपरिवर्तन की संख्या जब r निर्दिष्ट चीजें हमेशा एक साथ आती हैं - $r! (n−r+1)!$
N असमान तत्वों के क्रमपरिवर्तन की संख्या जब r निर्दिष्ट चीजें कभी एक साथ नहीं आती हैं - $n!–[r! (n−r+1)!]$
N विभिन्न तत्वों के परिपत्र क्रमपरिवर्तन की संख्या x तत्वों को समय पर लिया गया = $^np_{x}/x$
N विभिन्न चीजों के परिपत्र क्रमपरिवर्तन की संख्या = $^np_{n}/n$
कुछ समस्याएँ
Problem 1 - 6 अलग-अलग कार्डों के एक समूह से, हम इसे कितने तरीकों से अनुमति दे सकते हैं?
Solution - जैसा कि हम 6 कार्ड के डेक से एक बार में 6 कार्ड ले रहे हैं, क्रमचय होगा $^6P_{6} = 6! = 720$
Problem 2 - शब्द 'READER' के अक्षरों को कितने तरीकों से व्यवस्थित किया जा सकता है?
Solution - ER READER ’शब्द में 6 अक्षर शब्द (2 E, 1 A, 1D और 2R) हैं।
क्रमोन्नति होगी $= 6! /\: [(2!) (1!)(1!)(2!)] = 180.$
Problem 3 - 'ऑरेंज' शब्द के अक्षरों को किस तरह से व्यवस्थित किया जा सकता है ताकि व्यंजन केवल समान पदों पर ही कब्जा कर लें?
Solution- 'ऑरेंज' शब्द में 3 स्वर और 3 व्यंजन हैं। आपस में व्यंजन की व्यवस्था करने के तरीकों की संख्या$= ^3P_{3} = 3! = 6$। शेष 3 खाली स्थानों को 3 स्वरों में भरा जाएगा$^3P_{3} = 3! = 6$तरीके। इसलिए, क्रमपरिवर्तन की कुल संख्या है$6 \times 6 = 36$
युग्म
ए combination कुछ दिए गए तत्वों का चयन होता है जिसमें कोई फर्क नहीं पड़ता।
N चीजों के सभी संयोजनों की संख्या, जिन्हें एक समय में r लिया जाता है -
$$^nC_{ { r } } = \frac { n! } { r!(n-r)! }$$
Problem 1
सेट के सबसेट की संख्या ज्ञात कीजिए $\lbrace1, 2, 3, 4, 5, 6\rbrace$ 3 तत्व होने।
Solution
सेट की कार्डिनैलिटी 6 है और हमें सेट से 3 तत्वों को चुनना होगा। यहां, ऑर्डर देने से कोई फर्क नहीं पड़ता। इसलिए, सबसेट की संख्या होगी$^6C_{3} = 20$।
Problem 2
एक कमरे में 6 पुरुष और 5 महिलाएं हैं। कमरे से हम 3 पुरुषों और 2 महिलाओं को कितने तरीकों से चुन सकते हैं?
Solution
6 पुरुषों में से 3 पुरुषों को चुनने के तरीकों की संख्या है $^6C_{3}$ और 5 महिलाओं में से 2 महिलाओं को चुनने के तरीकों की संख्या है $^5C_{2}$
इसलिए, तरीकों की कुल संख्या है - $^6C_{3} \times ^5C_{2} = 20 \times 10 = 200$
Problem 3
आप कुल 9 छात्रों में से 3 छात्रों के 3 अलग-अलग समूहों में से कितने तरीके चुन सकते हैं?
Solution
आइए हम समूहों को 1, 2 और 3 के रूप में संख्या दें
1 सेंट समूह के लिए 3 छात्रों को चुनने के लिए , तरीकों की संख्या -$^9C_{3}$
1 समूह चुनने के बाद 2 एन डी समूह के लिए 3 छात्रों को चुनने के तरीकों की संख्या -$^6C_{3}$
1 सेंट और 2 एन डी समूह चुनने के बाद 3 आरडी समूह के लिए 3 छात्रों को चुनने के तरीकों की संख्या -$^3C_{3}$
इसलिए, तरीकों की कुल संख्या $= ^9C_{3} \times ^6C_{3} \times ^3C_{3} = 84 \times 20 \times 1 = 1680$
पास्कल की पहचान
पास्कल की पहचान, पहले 17 वीं शताब्दी में ब्लाइस पास्कल द्वारा निकाली गई थी, जिसमें कहा गया था कि n तत्वों से k तत्वों को चुनने के तरीकों की संख्या (n-1) तत्वों से चुनने के तरीकों की संख्या (k-1) के योग के बराबर है। और n-1 तत्वों से तत्वों को चुनने के तरीकों की संख्या।
गणितीय रूप से, किसी भी सकारात्मक पूर्णांक k और n के लिए: $^nC_{k} = ^n{^-}^1C_{k-1} + ^n{^-}^1{C_k}$
Proof -
$$^n{^-}^1C_{k-1} + ^n{^-}^1{C_k}$$
$= \frac{ (n-1)! } { (k-1)!(n-k)! } + \frac{ (n-1)! } { k!(n-k-1)! }$
$= (n-1)!(\frac{ k } { k!(n-k)! } + \frac{ n-k } { k!(n-k)! } )$
$= (n-1)! \frac{ n } { k!(n-k)! }$
$= \frac{ n! } { k!(n-k)! }$
$= n_{ C_{ k } }$
कबूतर का सिद्धांत
1834 में, जर्मन गणितज्ञ, पीटर गुस्ताव लेजेयुन डिरिचलेट ने एक सिद्धांत कहा, जिसे उन्होंने दराज सिद्धांत कहा। अब, यह कबूतर सिद्धांत के रूप में जाना जाता है।
Pigeonhole Principleबताता है कि अगर कुल कबूतरों की तुलना में कम कबूतर के छेद होते हैं और प्रत्येक कबूतर को एक कबूतर के छेद में डाल दिया जाता है, तो एक से अधिक कबूतर के साथ कम से कम एक कबूतर का छेद होना चाहिए। यदि n कबूतरों को m कबूतर में डाल दिया जाता है, जहां n> m होता है, तो एक से अधिक कबूतर के साथ एक छेद होता है।
उदाहरण
एक कमरे में दस आदमी हैं और वे हैंडशेक में हिस्सा ले रहे हैं। यदि प्रत्येक व्यक्ति कम से कम एक बार हाथ हिलाता है और कोई भी आदमी एक ही आदमी के हाथ को एक से अधिक बार नहीं हिलाता है तो दो पुरुषों ने एक ही संख्या में भाग लिया।
30 की कक्षा में कम से कम दो लोग होने चाहिए जिनका नाम उसी वर्णमाला से शुरू होता है।
समावेशन-बहिष्करण सिद्धांत
Inclusion-exclusion principleकई गैर-असहमति सेटों के संघ की कार्डिनल संख्या की गणना करता है। दो सेट A और B के लिए, सिद्धांत कहता है -
$|A \cup B| = |A| + |B| - |A \cap B|$
तीन सेट A, B और C के लिए, सिद्धांत कहता है -
$|A \cup B \cup C | = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C |$
सामान्यीकृत सूत्र -
$|\bigcup_{i=1}^{n}A_i|=\sum\limits_{1\leq i<j<k\leq n}|A_i \cap A_j|+\sum\limits_{1\leq i<j<k\leq n}|A_i \cap A_j \cap A_k|- \dots +(-1)^{\pi-1}|A_1 \cap \dots \cap A_2|$
Problem 1
1 से 50 तक के कितने पूर्णांक 2 या 3 के गुणक हैं लेकिन दोनों नहीं?
Solution
1 से 100 तक हैं $50/2 = 25$ संख्या जो 2 के गुणक हैं।
वहां $50/3 = 16$ संख्या जो 3 के गुणक हैं।
वहां $50/6 = 8$ संख्या जो 2 और 3 दोनों के गुणक हैं।
इसलिए, $|A|=25$, $|B|=16$ तथा $|A \cap B|= 8$।
$|A \cup B| = |A| + |B| - |A \cap B| = 25 + 16 - 8 = 33$
Problem 2
50 छात्रों के समूह में 24 कोल्ड ड्रिंक की तरह और 36 को हॉट ड्रिंक की तरह और प्रत्येक छात्र को कम से कम दो ड्रिंक पसंद हैं। कॉफी और चाय दोनों को कितने पसंद हैं?
Solution
बता दें कि X उन छात्रों का सेट है जो कोल्ड ड्रिंक पसंद करते हैं और Y ऐसे लोगों का सेट होते हैं जिन्हें हॉट ड्रिंक पसंद है।
इसलिए, $| X \cup Y | = 50$, $|X| = 24$, $|Y| = 36$
$|X \cap Y| = |X| + |Y| - |X \cup Y| = 24 + 36 - 50 = 60 - 50 = 10$
इसलिए, ऐसे 10 छात्र हैं जो चाय और कॉफी दोनों पसंद करते हैं।
गिनती की अवधारणाओं से निकटता संभावित है। हम अक्सर मौका के खेल के परिणामों का अनुमान लगाने की कोशिश करते हैं, जैसे कार्ड गेम, स्लॉट मशीन और लॉटरी; यानी हम इस संभावना या संभावना को खोजने की कोशिश करते हैं कि कोई विशेष परिणाम प्राप्त किया जाए।
Probabilityकिसी घटना के घटित होने की संभावना को खोजने के रूप में संकल्पित किया जा सकता है। गणितीय रूप से, यह यादृच्छिक प्रक्रियाओं और उनके परिणामों का अध्ययन है। प्रायिकता के नियमों में विभिन्न क्षेत्रों जैसे आनुवांशिकी, मौसम पूर्वानुमान, जनमत सर्वेक्षण, शेयर बाजार आदि में व्यापक प्रयोज्यता है।
मूल अवधारणा
संभावना सिद्धांत का आविष्कार 17 वीं शताब्दी में दो फ्रांसीसी गणितज्ञों, ब्लेज़ पास्कल और पियरे डी फ़र्मेट द्वारा किया गया था, जो मौका के संबंध में गणितीय समस्याओं से जूझ रहे थे।
संभावना के विवरण पर आगे बढ़ने से पहले, आइए हम कुछ परिभाषाओं की अवधारणा प्राप्त करें।
Random Experiment- एक प्रयोग जिसमें सभी संभावित परिणामों को जाना जाता है और सटीक आउटपुट की भविष्यवाणी नहीं की जा सकती है, इसे यादृच्छिक प्रयोग कहा जाता है। एक उचित सिक्का टॉस करना यादृच्छिक प्रयोग का एक उदाहरण है।
Sample Space- जब हम एक प्रयोग करते हैं, तो सभी संभावित परिणामों के सेट S को नमूना स्थान कहा जाता है। यदि हम एक सिक्का, नमूना स्थान टॉस करते हैं$S = \left \{ H, T \right \}$
Event- नमूना स्थान के किसी भी सबसेट को एक घटना कहा जाता है। एक सिक्का उछालने के बाद, शीर्ष पर सिर प्राप्त करना एक घटना है।
शब्द "संभावना" का अर्थ किसी विशेष घटना के होने की संभावना है। सबसे अच्छा हम कह सकते हैं कि संभावना के विचार का उपयोग करते हुए, वे होने की कितनी संभावना है।
$Probability\:of\:occurence\:of\:an\:event = \frac{Total\:number\:of\:favourable \: outcome}{Total\:number\:of\:Outcomes}$
किसी भी घटना की घटना 0% और 100% के बीच भिन्न होती है, संभावना 0 और 1 के बीच भिन्न होती है।
संभावना खोजने के लिए कदम
चरण 1 - प्रयोग के सभी संभावित परिणामों की गणना करें।
चरण 2 - प्रयोग के अनुकूल परिणामों की संख्या की गणना करें।
चरण 3 - संबंधित संभावना फार्मूला लागू करें।
सिक्का उछालना
यदि एक सिक्का उछाला जाता है, तो दो संभावित परिणाम हैं - प्रमुख $(H)$ या पूंछता है $(T)$
तो, परिणामों की कुल संख्या = 2
इसलिए, एक प्रमुख होने की संभावना $(H)$ शीर्ष पर 1/2 है और पूंछ प्राप्त करने की संभावना है $(T)$ शीर्ष पर 1/2 है
एक पासा फेंकना
जब एक पासा फेंका जाता है, तो छह संभावित परिणाम शीर्ष पर हो सकते हैं - $1, 2, 3, 4, 5, 6$।
संख्याओं में से किसी एक की संभावना 1/6 है
सम संख्याएँ प्राप्त करने की संभावना 3/6 = 1/2 है
विषम संख्या प्राप्त करने की संभावना 3/6 = 1/2 है
एक डेक से कार्ड ले रहा है
52 कार्डों के एक डेक से, यदि एक कार्ड उठाया जाता है, तो इक्का के खींचे जाने की संभावना का पता लगा सकते हैं और खींचे गए हीरे की संभावना का भी पता लगा सकते हैं।
संभावित परिणामों की कुल संख्या - 52
एक इक्का होने के परिणाम - 4
इक्का = 4/52 = 1/13 होने की संभावना
हीरा होने की संभावना = 13/52 = 1/4
प्रायिकता Axioms
किसी घटना की संभावना हमेशा 0 से 1 तक भिन्न होती है। $[0 \leq P(x) \leq 1]$
एक असंभव घटना के लिए संभावना 0 है और एक निश्चित घटना के लिए संभावना 1 है।
यदि एक घटना की घटना किसी अन्य घटना से प्रभावित नहीं होती है, तो उन्हें पारस्परिक रूप से अनन्य या असहमति कहा जाता है।
अगर $A_1, A_2....A_n$ तब परस्पर अनन्य / अप्रिय घटनाएँ होती हैं $P(A_i \cap A_j) = \emptyset $ के लिये $i \ne j$ तथा $P(A_1 \cup A_2 \cup.... A_n) = P(A_1) + P(A_2)+..... P(A_n)$
संभाव्यता के गुण
अगर दो घटनाएँ हैं $x$ तथा $\overline{x}$जो पूरक हैं, तो पूरक घटना की संभावना है -
$$p(\overline{x}) = 1-p(x)$$
दो गैर-असंतुष्ट घटनाओं ए और बी के लिए, दो घटनाओं के मिलन की संभावना -
$P(A \cup B) = P(A) + P(B)$
यदि एक घटना A, दूसरी घटना B (यानी) का सबसेट है $A \subset B$), तब A की संभावना B की संभावना से कम या उसके बराबर है। $A \subset B$ का तात्पर्य $P(A) \leq p(B)$
सशर्त संभाव्यता
किसी घटना B की सशर्त संभाव्यता यह संभावना है कि घटना घटित होगी एक घटना A पहले ही हो चुकी है। इसे इस प्रकार लिखा गया है$P(B|A)$।
गणितीय रूप से - $ P(B|A) = P(A \cap B)/ P(A)$
यदि घटना A और B पारस्परिक रूप से अनन्य हैं, तो घटना A के बाद की घटना B की सशर्त प्रायिकता होगी, जो कि घटना B की संभावना है $P(B)$।
Problem 1
एक देश में सभी किशोरों में से 50% के पास एक साइकिल है और सभी किशोरों के 30% के पास एक बाइक और साइकिल है। क्या संभावना है कि एक किशोर बाइक का मालिक है जो कि एक साइकिल का मालिक है?
Solution
मान लेते हैं कि A केवल एक चक्र के मालिक किशोरों की घटना है और B केवल बाइक के स्वामी किशोरों की घटना है।
इसलिए, $P(A) = 50/100 = 0.5$ तथा $P(A \cap B) = 30/100 = 0.3$ दी गई समस्या से।
$P(B|A) = P(A \cap B)/ P(A) = 0.3/ 0.5 = 0.6$
इसलिए, संभावना है कि एक किशोर बाइक का मालिक है, यह देखते हुए कि एक साइकिल का मालिक 60% है।
Problem 2
एक कक्षा में, 50% सभी छात्र क्रिकेट खेलते हैं और 25% सभी छात्र क्रिकेट और वॉलीबॉल खेलते हैं। क्या संभावना है कि एक छात्र वॉलीबॉल खेलता है जिसे देखते हुए छात्र क्रिकेट खेलता है?
Solution
आइए मान लेते हैं कि A केवल क्रिकेट खेलने वाले छात्रों की घटना है और B केवल वॉलीबॉल खेलने वाले छात्रों की घटना है।
इसलिए, $P(A) = 50/100 =0.5$ तथा $P(A \cap B) = 25/ 100 =0.25$ दी गई समस्या से।
$P\lgroup B\rvert A \rgroup= P\lgroup A\cap B\rgroup/P\lgroup A \rgroup =0.25/0.5=0.5$
इसलिए, एक छात्र द्वारा खेली जाने वाली वालीबॉल खेलने की संभावना 50% है।
Problem 3
छह अच्छे लैपटॉप और तीन दोषपूर्ण लैपटॉप मिश्रित हैं। दोषपूर्ण लैपटॉप को खोजने के लिए उन सभी को यादृच्छिक रूप से एक-एक करके परीक्षण किया जाता है। पहले दो पिक में दोनों दोषपूर्ण लैपटॉप को खोजने की संभावना क्या है?
Solution
आज्ञा देना एक घटना है कि हम पहले परीक्षण में एक दोषपूर्ण लैपटॉप मिल और बी घटना है कि हम दूसरे परीक्षण में एक दोषपूर्ण लैपटॉप मिल जाए।
इसलिये, $P(A \cap B) = P(A)P(B|A) =3/9 \times 2/8 = 1/12$
बेयस की प्रमेय
Theorem - यदि I और B दो परस्पर अनन्य घटनाएँ हैं, तो कहाँ $P(A)$ ए की संभावना है और $P(B)$ बी की संभावना है, $P(A | B)$ A की संभावना है कि B सत्य है। $P(B | A)$ B की संभावना है कि A सत्य है, तो बेयस प्रमेय कहता है -
$$P(A|B) = \frac{P(B|A) P(A)}{\sum_{i = 1}^{n}P(B|Ai)P(Ai)}$$
Bayes 'प्रमेय के अनुप्रयोग
उन स्थितियों में जहां नमूना स्थान की सभी घटनाएं पारस्परिक रूप से अनन्य घटनाएं हैं।
उन स्थितियों में जहां या तो $P( A_i \cap B )$ प्रत्येक के लिए $A_i$ या $P( A_i )$ तथा $P(B|A_i)$ प्रत्येक के लिए $A_i$ ज्ञात है।
Problem
तीन पेन-स्टैंड पर विचार करें। पहले पेन-स्टैंड में 2 लाल पेन और 3 नीले पेन शामिल हैं; दूसरे में 3 लाल पेन और 2 नीले पेन हैं; और तीसरे में 4 लाल कलम और 1 नीला पेन है। चुने जाने के लिए प्रत्येक पेन-स्टैंड की समान संभावना है। यदि एक कलम यादृच्छिक रूप से तैयार की जाती है, तो क्या संभावना है कि यह एक लाल कलम है?
Solution
लश्कर $A_i$घटना में है कि मैं हो वें कलम स्टैंड चयन किया जाता है।
यहाँ, मैं = 1,2,3।
चूंकि पेन-स्टैंड चुनने की संभावना बराबर है, $P(A_i) = 1/3$
बता दें कि B एक लाल पेन है।
संभावना है कि पहले पेन-स्टैंड के पांच कलमों के बीच एक लाल कलम चुना जाता है,
$P(B|A_1) = 2/5$
दूसरे पेन-स्टैंड के पाँच कलमों के बीच लाल पेन चुने जाने की संभावना
$P(B|A_2) = 3/5$
तीसरे पेन-स्टैंड के पाँच कलमों के बीच लाल पेन चुने जाने की संभावना
$P(B|A_3) = 4/5$
बेयस के प्रमेय के अनुसार,
$P(B) = P(A_1).P(B|A_1) + P(A_2).P(B|A_2) + P(A_3).P(B|A_3)$
$= 1/3 . 2/5\: +\: 1/3 . 3/5\: +\: 1/3 . 4/5$
$= 3/5$
Mathematical induction, प्राकृतिक संख्याओं के लिए परिणाम सिद्ध करने या कथन स्थापित करने की एक तकनीक है। यह भाग विभिन्न उदाहरणों के माध्यम से विधि का चित्रण करता है।
परिभाषा
Mathematical Induction एक गणितीय तकनीक है जिसका उपयोग किसी कथन को सिद्ध करने के लिए किया जाता है, एक सूत्र या एक प्रमेय हर प्राकृतिक संख्या के लिए सही है।
तकनीक में कथन को साबित करने के लिए दो चरण शामिल हैं, जैसा कि नीचे बताया गया है -
Step 1(Base step) - यह साबित करता है कि प्रारंभिक मूल्य के लिए एक बयान सही है।
Step 2(Inductive step)- यह साबित होता है कि यदि कथन n वें पुनरावृत्ति (या संख्या n ) के लिए सत्य है, तो यह (n + 1) वें पुनरावृत्ति (या संख्या n + 1 ) के लिए भी सही है ।
इसे कैसे करना है
Step 1- एक प्रारंभिक मूल्य पर विचार करें जिसके लिए कथन सत्य है। यह दिखाया जाना है कि कथन n = प्रारंभिक मान के लिए सही है।
Step 2- मान लें कि कथन n = k के किसी भी मान के लिए सही है । फिर सिद्ध करें कि कथन n = k + 1 के लिए सत्य है । हम वास्तव में n = k + 1 को दो भागों में तोड़ते हैं , एक भाग n = k (जो पहले से सिद्ध है) और दूसरे भाग को सिद्ध करने का प्रयास करते हैं।
समस्या 1
$3^n-1$ n = 1, 2, के लिए 2 का एक बहु है ...
Solution
Step 1 - के लिए $n = 1, 3^1-1 = 3-1 = 2$ जो कि 2 का गुणक है
Step 2 - मान लेते हैं $3^n-1$ के लिए सच है $n=k$, इसलिये, $3^k -1$ सच है (यह एक धारणा है)
हमें यह साबित करना होगा $3^{k+1}-1$ 2 का एक बहु भी है
$3^{k+1} - 1 = 3 \times 3^k - 1 = (2 \times 3^k) + (3^k - 1)$
पहला भाग $(2 \times 3k)$ 2 का एक बहु होना और दूसरा भाग होना निश्चित है $(3k -1)$ हमारी पूर्व धारणा के रूप में भी सत्य है।
इसलिये, $3^{k+1} – 1$ 2 का एक बहु है।
तो, यह साबित होता है कि $3^n – 1$ 2 का एक बहु है।
समस्या २
$1 + 3 + 5 + ... + (2n-1) = n^2$ के लिये $n = 1, 2, \dots $
Solution
Step 1 - के लिए $n=1, 1 = 1^2$, इसलिए, चरण 1 संतुष्ट है।
Step 2 - मान लें कि कथन सही है $n=k$।
इसलिये, $1 + 3 + 5 + \dots + (2k-1) = k^2$ सच है (यह एक धारणा है)
हमें यह साबित करना होगा $1 + 3 + 5 + ... + (2(k+1)-1) = (k+1)^2$ भी रखती है
$1 + 3 + 5 + \dots + (2(k+1) - 1)$
$= 1 + 3 + 5 + \dots + (2k+2 - 1)$
$= 1 + 3 + 5 + \dots + (2k + 1)$
$= 1 + 3 + 5 + \dots + (2k - 1) + (2k + 1)$
$= k^2 + (2k + 1)$
$= (k + 1)^2$
इसलिए, $1 + 3 + 5 + \dots + (2(k+1) - 1) = (k+1)^2$ जो चरण 2 को संतुष्ट करता है।
इसलिये, $1 + 3 + 5 + \dots + (2n - 1) = n^2$ सिद्ध है।
समस्या 3
साबित करो $(ab)^n = a^nb^n$ हर प्राकृतिक संख्या के लिए सही है $n$
Solution
Step 1 - के लिए $n=1, (ab)^1 = a^1b^1 = ab$, इसलिए, चरण 1 संतुष्ट है।
Step 2 - मान लें कि कथन सही है $n=k$, इसलिये, $(ab)^k = a^kb^k$ सच है (यह एक धारणा है)।
हमें यह साबित करना होगा $(ab)^{k+1} = a^{k+1}b^{k+1}$ धारण भी करें
दिया हुआ, $(ab)^k = a^k b^k$
या, $(ab)^k (ab) = (a^k b^k ) (ab)$ [दोनों पक्षों को 'ab' से गुणा करें]
या, $(ab)^{k+1} = (aa^k) ( bb^k)$
या, $(ab)^{k+1} = (a^{k+1}b^{k+1})$
इसलिए, चरण 2 साबित हुआ है।
इसलिए, $(ab)^n = a^nb^n$ हर प्राकृतिक संख्या n के लिए सही है।
मजबूत प्रेरण
मजबूत प्रेरण गणितीय प्रेरण का दूसरा रूप है। इस प्रेरण तकनीक के माध्यम से, हम यह साबित कर सकते हैं कि एक प्रस्ताव कार्य,$P(n)$ सभी सकारात्मक पूर्णांकों के लिए सही है, $n$, निम्नलिखित चरणों का उपयोग कर -
Step 1(Base step) - यह साबित करता है कि प्रारंभिक प्रस्ताव $P(1)$ सच।
Step 2(Inductive step) - यह साबित करता है कि सशर्त बयान $[P(1) \land P(2) \land P(3) \land \dots \land P(k)] → P(k + 1)$ सकारात्मक पूर्णांकों के लिए सही है $k$।
इस अध्याय में, हम चर्चा करेंगे कि पुनरावर्ती तकनीक अनुक्रमों को कैसे प्राप्त कर सकती हैं और गिनती की समस्याओं को हल करने के लिए उपयोग किया जा सकता है। एक पुनरावर्ती तरीके से अनुक्रम की शर्तों को खोजने की प्रक्रिया को कहा जाता हैrecurrence relation। हम रैखिक पुनरावृत्ति संबंधों और उनके समाधान के सिद्धांत का अध्ययन करते हैं। अंत में, हम पुनरावृत्ति संबंधों को हल करने के लिए जनरेटिंग फ़ंक्शंस पेश करते हैं।
परिभाषा
एक पुनरावृत्ति संबंध एक समीकरण है जो पुनरावर्ती अनुक्रम को परिभाषित करता है जहां अगला शब्द पिछले शब्दों का एक फ़ंक्शन है (व्यक्त करना $F_n$ के कुछ संयोजन के रूप में $F_i$ साथ में $i < n$)।
Example - फाइबोनैचि श्रृंखला - $F_n = F_{n-1} + F_{n-2}$, हनोई का टॉवर - $F_n = 2F_{n-1} + 1$
रैखिक पुनरावृत्ति संबंध
डिग्री k या ऑर्डर k का रैखिक पुनरावर्तन समीकरण एक पुनरावृत्ति समीकरण है जो प्रारूप में है $x_n= A_1 x_{n-1}+ A_2 x_{n-1}+ A_3 x_{n-1}+ \dots A_k x_{n-k} $($A_n$ एक स्थिर और है $A_k \neq 0$) पहले-डिग्री बहुपद के रूप में संख्याओं के अनुक्रम पर।
ये रेखीय पुनरावृत्ति समीकरणों के कुछ उदाहरण हैं -
| पुनरावृत्ति संबंध | प्रारंभिक मूल्य | समाधान |
|---|---|---|
| F n = F n-1 + F n-2 | एक 1 = एक 2 = 1 | फाइबोनैचि संख्या |
| F n = F n-1 + F n-2 | एक 1 = 1, एक 2 = 3 | लुकास संख्या |
| एफ एन = एफ एन -2 + एफ एन -3 | एक 1 = एक 2 = एक 3 = 1 | पादोवन क्रम |
| एफ एन = 2 एफ एन -1 + एफ एन -2 | एक 1 = 0, एक 2 = 1 | पेल नंबर |
रैखिक पुनरावृत्ति संबंध को कैसे हल करें
मान लीजिए, एक दो क्रमबद्ध रैखिक पुनरावृत्ति संबंध है - $F_n = AF_{n-1} +BF_{n-2}$ जहां A और B वास्तविक संख्या हैं।
उपरोक्त पुनरावृत्ति संबंध के लिए विशेषता समीकरण है -
$$x^2 - Ax - B = 0$$
जड़ों को खोजने के दौरान तीन मामले हो सकते हैं -
Case 1 - यदि यह समीकरण कारक के रूप में $(x- x_1)(x- x_1) = 0$ और यह दो अलग वास्तविक जड़ें पैदा करता है $x_1$ तथा $x_2$, फिर $F_n = ax_1^n+ bx_2^n$समाधान है। [यहाँ, ए और बी स्थिरांक हैं]
Case 2 - यदि यह समीकरण कारक के रूप में $(x- x_1)^2 = 0$ और यह एकल वास्तविक जड़ पैदा करता है $x_1$, फिर $F_n = a x_1^n+ bn x_1^n$ समाधान है।
Case 3 - यदि समीकरण दो अलग-अलग जटिल जड़ें पैदा करता है, $x_1$ तथा $x_2$ ध्रुवीय रूप में $x_1 = r \angle \theta$ तथा $x_2 = r \angle(- \theta)$, फिर $F_n = r^n (a cos(n\theta)+ b sin(n\theta))$ समाधान है।
Problem 1
पुनरावृत्ति संबंध को हल करें $F_n = 5F_{n-1} - 6F_{n-2}$ कहाँ पे $F_0 = 1$ तथा $F_1 = 4$
Solution
पुनरावृत्ति संबंध की विशेषता समीकरण है -
$$x^2 - 5x + 6 = 0,$$
इसलिए, $(x - 3) (x - 2) = 0$
इसलिए, जड़ें हैं -
$x_1 = 3$ तथा $x_2 = 2$
जड़ें वास्तविक और विशिष्ट हैं। तो, यह केस 1 के रूप में है
इसलिए, समाधान है -
$$F_n = ax_1^n + bx_2^n$$
यहाँ, $F_n = a3^n + b2^n\ (As\ x_1 = 3\ and\ x_2 = 2)$
इसलिए,
$1 = F_0 = a3^0 + b2^0 = a+b$
$4 = F_1 = a3^1 + b2^1 = 3a+2b$
इन दो समीकरणों को हल करते हुए, हम प्राप्त करते हैं $ a = 2$ तथा $b = -1$
इसलिए, अंतिम समाधान है -
$$F_n = 2.3^n + (-1) . 2^n = 2.3^n - 2^n $$
Problem 2
पुनरावृत्ति संबंध हल करें - $F_n = 10F_{n-1} - 25F_{n-2}$ कहाँ पे $F_0 = 3$ तथा $F_1 = 17$
Solution
पुनरावृत्ति संबंध की विशेषता समीकरण है -
$$ x^2 - 10x -25 = 0$$
इसलिए $(x - 5)^2 = 0$
इसलिए, वहाँ एक असली जड़ है $x_1 = 5$
जैसा कि एकल वास्तविक मूल्यवान रूट है, यह केस 2 के रूप में है
इसलिए, समाधान है -
$F_n = ax_1^n + bnx_1^n$
$3 = F_0 = a.5^0 +(b)(0.5)^0 = a$
$17 = F_1 = a.5^1 + b.1.5^1 = 5a+5b$
इन दो समीकरणों को हल करते हुए, हम प्राप्त करते हैं $a = 3$ तथा $b = 2/5$
इसलिए, अंतिम समाधान है - $F_n = 3.5^n +( 2/5) .n.2^n $
Problem 3
पुनरावृत्ति संबंध को हल करें $F_n = 2F_{n-1} - 2F_{n-2}$ कहाँ पे $F_0 = 1$ तथा $F_1 = 3$
Solution
पुनरावृत्ति संबंध की विशेषता समीकरण है -
$$x^2 -2x -2 = 0$$
इसलिए, जड़ें हैं -
$x_1 = 1 + i$ तथा $x_2 = 1 - i$
ध्रुवीय रूप में,
$x_1 = r \angle \theta$ तथा $x_2 = r \angle(- \theta),$ कहाँ पे $r = \sqrt 2$ तथा $\theta = \frac{\pi}{4}$
जड़ें काल्पनिक हैं। तो, यह केस 3 के रूप में है।
इसलिए, समाधान है -
$F_n = (\sqrt 2 )^n (a cos(n .\sqcap /4) + b sin(n .\sqcap /4))$
$1 = F_0 = (\sqrt 2 )^0 (a cos(0 .\sqcap /4) + b sin(0 .\sqcap /4) ) = a$
$3 = F_1 = (\sqrt 2 )^1 (a cos(1 .\sqcap /4) + b sin(1 . \sqcap /4) ) = \sqrt 2 ( a/ \sqrt 2 + b/ \sqrt 2)$
इन दो समीकरणों को हल करने से हमें मिलता है $a = 1$ तथा $b = 2$
इसलिए, अंतिम समाधान है -
$F_n = (\sqrt 2 )^n (cos(n .\pi /4 ) + 2 sin(n .\pi /4 ))$
गैर-सजातीय पुनरावृत्ति संबंध और विशेष समाधान
यदि यह प्रपत्र में है, तो पुनरावृत्ति संबंध को गैर-सजातीय कहा जाता है
$F_n = AF_{n-1} + BF_{n-2} + f(n)$ कहाँ पे $f(n) \ne 0$
इसका संबद्ध सजातीय पुनरावृत्ति संबंध है $F_n = AF_{n–1} + BF_{n-2}$
समाधान $(a_n)$ गैर-सजातीय पुनरावृत्ति संबंध के दो भाग हैं।
पहला भाग समाधान है $(a_h)$ संबंधित सजातीय पुनरावृत्ति संबंध और दूसरा भाग विशेष समाधान है $(a_t)$।
$$a_n=a_h+a_t$$
पहले भाग का समाधान पिछले अनुभाग में चर्चा की गई प्रक्रियाओं का उपयोग करके किया जाता है।
विशेष समाधान खोजने के लिए, हम एक उपयुक्त परीक्षण समाधान पाते हैं।
लश्कर $f(n) = cx^n$; लश्कर$x^2 = Ax + B$ संबंधित सजातीय पुनरावृत्ति संबंध और जाने की विशेषता समीकरण हो $x_1$ तथा $x_2$ इसकी जड़ें बनो।
अगर $x \ne x_1$ तथा $x \ne x_2$, फिर $a_t = Ax^n$
अगर $x = x_1$, $x \ne x_2$, फिर $a_t = Anx^n$
अगर $x = x_1 = x_2$, फिर $a_t = An^2x^n$
उदाहरण
एक गैर-सजातीय पुनरावृत्ति संबंध होने दें $F_n = AF_{n–1} + BF_{n-2} + f(n)$ विशेषता जड़ों के साथ $x_1 = 2$ तथा $x_2 = 5$। के विभिन्न संभावित मूल्यों के लिए परीक्षण समाधान$f(n)$ इस प्रकार हैं -