ग्राफ और ग्राफ मॉडल

पिछला भाग तर्क, प्रमाण और समस्या को हल करने के लिए विभिन्न उपकरणों को सामने लाया। इस भाग में, हम असतत संरचनाओं का अध्ययन करेंगे जो कई वास्तविक जीवन की समस्या को तैयार करने का आधार बनती हैं।

दो असतत संरचनाएं जिन्हें हम कवर करेंगे वे रेखांकन और पेड़ हैं। एक ग्राफ़ बिंदुओं का एक समूह है, जिसे नोड्स या वर्टिस कहा जाता है, जो कि किनारों नामक रेखाओं के समूह द्वारा परस्पर जुड़े होते हैं। रेखांकन का अध्ययन, याgraph theory गणित, इंजीनियरिंग और कंप्यूटर विज्ञान के क्षेत्र में कई विषयों का एक महत्वपूर्ण हिस्सा है।

ग्राफ़ क्या है?

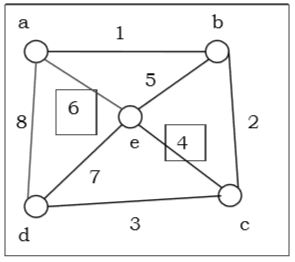
Definition - एक ग्राफ (जिसे $ G = (V, E) $ के रूप में दर्शाया गया है) एक गैर-रिक्त सेट है जिसमें कोने या नोड्स V और किनारों E का एक सेट है।

Example - हमें विचार करें, एक ग्राफ $ G = (V, E) $ है, जहां $ V = \ lbrace a, b, c, d \ rbrace $ और $ E = \ lbrace \ lbrace a, b \ rbrace, \ lbrace a , सी \ rbrace, \ lbrace b, c \ rbrace, \ lbrace c, d \ rbrace \ rbrace $

Degree of a Vertex - एक ग्राफ G की एक वर्टेक्स V की डिग्री (नीच द्वारा निरूपित) (V) किनारों की घटना की संख्या है, जो शीर्ष पर है।

शिखर	डिग्री	सम विषम
ए	2	यहाँ तक की
ख	2	यहाँ तक की
सी	3	अजीब
घ	1	अजीब

Even and Odd Vertex - यदि एक शीर्ष की डिग्री सम है, तो शीर्ष को एक सम शीर्ष कहा जाता है और यदि एक शीर्ष की डिग्री विषम है, तो शीर्ष को विषम शीर्ष कहा जाता है।

Degree of a Graph- एक ग्राफ की डिग्री उस ग्राफ की सबसे बड़ी शीर्ष डिग्री है। उपरोक्त ग्राफ के लिए ग्राफ की डिग्री 3 है।

The Handshaking Lemma - एक ग्राफ में, सभी शीर्षों के सभी अंशों का योग दो बार किनारों की संख्या के बराबर होता है।

रेखांकन के प्रकार

विभिन्न प्रकार के ग्राफ़ हैं, जिन्हें हम निम्नलिखित अनुभाग में सीखेंगे।

नल का ग्राफ

एक अशक्त ग्राफ़ में कोई किनारा नहीं है। $ N $ वर्नों के शून्य ग्राफ को $ N_n $ द्वारा निरूपित किया जाता है

सरल ग्राफ

ग्राफ़ को सरल ग्राफ़ / सख्त ग्राफ़ कहा जाता है यदि ग्राफ़ अप्रत्यक्ष है और इसमें कोई लूप या एकाधिक किनारे नहीं हैं।

बहु ग्राफ

यदि ग्राफ़ में एक ही सेट के बीच कई किनारों को अनुमति दी जाती है, तो इसे मल्टीग्राफ कहा जाता है। दूसरे शब्दों में, यह कम से कम एक लूप या कई किनारों वाला एक ग्राफ है।

निर्देशित और अप्रत्यक्ष ग्राफ़

एक ग्राफ $ G = (V, E) $ को एक निर्देशित ग्राफ़ कहा जाता है यदि किनारे सेट ऑर्डर किए गए शीर्ष जोड़ी से बना होता है और एक बढ़त को अप्रत्यक्ष कहा जाता है यदि किनारे सेट अनियंत्रित वर्टेक्स जोड़ी से बना होता है।

कनेक्टेड और डिस्कनेक्टेड ग्राफ़

एक ग्राफ जुड़ा हुआ है अगर ग्राफ के दो कोने एक रास्ते से जुड़े हुए हैं; जबकि एक ग्राफ काट दिया जाता है यदि ग्राफ़ के कम से कम दो कोने एक पथ से जुड़े नहीं हैं। यदि एक ग्राफ G को डिस्कनेक्ट किया जाता है, तो $ G $ के प्रत्येक अधिकतम जुड़े सबग्राफ को ग्राफ $ G $ का जुड़ा घटक कहा जाता है।

नियमित ग्राफ

एक ग्राफ नियमित है अगर ग्राफ के सभी कोने एक ही डिग्री हैं। डिग्री $ r $ के एक नियमित ग्राफ G में, $ G $ के प्रत्येक शीर्ष की डिग्री r है।

पूरा ग्राफ

एक ग्राफ को पूरा ग्राफ कहा जाता है यदि हर दो कोने जोड़े एक किनारे से जुड़ते हैं। N कोने के साथ पूरा ग्राफ $ K_n $ द्वारा निरूपित किया गया है

साइकिल ग्राफ

यदि एक ग्राफ में एक चक्र होता है, तो इसे चक्र ग्राफ कहा जाता है। N कोने के साथ चक्र ग्राफ को $ C_n $ द्वारा निरूपित किया जाता है

द्विदलीय आलेख

यदि ग्राफ़ G का वर्टेक्स-सेट दो डिसऑइंट सेट में, $ V_1 $ और $ V_2 $ में विभाजित किया जा सकता है, तो इस तरह से कि ग्राफ़ में प्रत्येक किनारे $ V_1 में एक शीर्ष पर $ V_2 $ में एक शीर्ष से जुड़ जाता है। और G में कोई किनारा नहीं है जो $ V_1 $ में दो कोने जोड़ते हैं और $ V_2 $ में दो कोने हैं, तो ग्राफ $ G $ को एक द्विदलीय ग्राफ कहा जाता है।

बिपर्टाइट ग्राफ को पूरा करें

एक पूर्ण द्विपदीय ग्राफ एक द्विदलीय ग्राफ है जिसमें पहले सेट में प्रत्येक शीर्ष दूसरे सेट में प्रत्येक एकल शीर्ष के साथ जुड़ जाता है। पूरा द्विदलीय ग्राफ $ K_ {x, y} $ द्वारा निरूपित किया जाता है, जहां ग्राफ $ G $ में पहले सेट में $ x $ कोने होते हैं और दूसरे सेट में $ y $ कोने होते हैं।

रेखांकन का प्रतिनिधित्व

एक ग्राफ का प्रतिनिधित्व करने के लिए मुख्य रूप से दो तरीके हैं -

• सहखंडज मैट्रिक्स
• आसन्न सूची

सहखंडज मैट्रिक्स

एक निकटता मैट्रिक्स $ A [V] [V] $ आकार का एक 2D सरणी $ V \ गुना V $ है जहां $ V $ एक अप्रत्यक्ष ग्राफ़ में कोने की संख्या है। यदि $ V_x $ से $ V_y $ के बीच बढ़त है तो $ A [V_x] [V_y] = 1 $ और $ A [V_y] [V_x] = 1 $ का मान, अन्यथा मूल्य शून्य हो जाएगा। और एक निर्देशित ग्राफ के लिए, यदि $ V_x $ से $ V_y $ के बीच कोई बढ़त है, तो $ A [V_x] [V_y] = 1 $ का मान, अन्यथा मान शून्य होगा।

Adjacency Matrix of an Undirected Graph

आइए हम निम्नलिखित अप्रत्यक्ष ग्राफ पर विचार करें और आसन्न मैट्रिक्स का निर्माण करें -

उपरोक्त अप्रत्यक्ष ग्राफ की निकटता मैट्रिक्स होगी -

	a	b	c	d
a	0	1	1	0
b	1	0	1	0
c	1	1	0	1
d	0	0	1	0

Adjacency Matrix of a Directed Graph

आइए हम निम्नलिखित निर्देशित ग्राफ पर विचार करें और इसके आसन्न मैट्रिक्स का निर्माण करें -

उपरोक्त निर्देशित ग्राफ की निकटता मैट्रिक्स होगी -

	a	b	c	d
a	0	1	1	0
b	0	0	1	0
c	0	0	0	1
d	0	0	0	0

आसन्न सूची

आसन्न सूची में, एक लिंक $ (A [V]) लिंक्ड सूची का $ $ V $ वर्टिस के साथ ग्राफ G को दर्शाने के लिए उपयोग किया जाता है। एक प्रविष्टि $ A [V_x] $ $ Vx-th ​​$ वर्टेक्स से सटे कोने की सूची से जुड़ी है। अप्रत्यक्ष ग्राफ की सन्निकटन सूची इस प्रकार है:

प्लेनर बनाम गैर-प्लानर ग्राफ

Planar graph- एक ग्राफ $ G $ को प्लेनर ग्राफ कहा जाता है अगर इसे बिना किसी किनारों को पार किए विमान में खींचा जा सकता है। यदि हम प्लेन को बिना क्रॉस क्रॉस के प्लेन में खींचते हैं, तो इसे प्लेन में ग्राफ को एम्बेड करना कहा जाता है।

Non-planar graph - एक ग्राफ नॉन-प्लानर है अगर इसे बिना प्लेन एज क्रॉसिंग के प्लेन में नहीं खींचा जा सकता।

समाकृतिकता

यदि दो ग्राफ़ G और H में समान संख्या में कोने जुड़े होते हैं, तो उन्हें आइसोमॉर्फिक ग्राफ़ ($ G \ cong H $ द्वारा निरूपित) कहा जाता है।

आइसोमोर्फिज्म की तुलना में गैर-आइसोमोर्फिज्म की जांच करना आसान है। यदि निम्न में से कोई भी स्थिति होती है, तो दो रेखांकन गैर-आइसोमॉर्फिक हैं -

• जुड़े हुए घटकों की संख्या भिन्न होती है
• वर्टेक्स-सेट कार्डिनैलिटी अलग हैं
• एज-सेट कार्डिनैलिटी अलग हैं
• डिग्री क्रम अलग हैं

उदाहरण

निम्नलिखित रेखीय समद्विबाहु हैं -

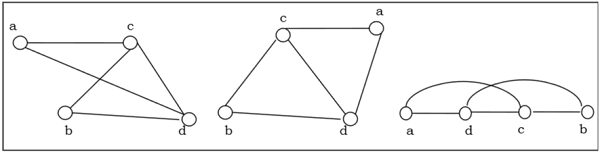
समरूपता

एक ग्राफोमोर्फिज्म एक ग्राफ $ G $ से एक ग्राफ $ H $ एक मैपिंग (एक विशेषण मानचित्रण नहीं हो सकता है) $ h: G \ rightarrow H $ ऐसे कि - $ (x, y) \ _ in (G) \ (h (x), h (y)) \ E (H) $ में। यह ग्राफ $ G $ के आसन्न कोने के आसन्न कोने में मैप करता है।

गुणसूत्रों के गुण

• यदि यह एक विशेषण मानचित्रण है तो एक समरूपता एक समरूपता है।

• होमोमोर्फिज्म हमेशा किनारों और एक ग्राफ की कनेक्टिविटी को बनाए रखता है।

• समरूपता की रचनाएँ भी समरूपताएँ हैं।

• यह पता लगाने के लिए कि क्या किसी अन्य ग्राफ़ के होमोमोर्फिक ग्राफ मौजूद है, एक एनपीकंप्लीट समस्या है।

यूलर ग्राफ़

एक जुड़ा हुआ ग्राफ $ G $ एक यूलर ग्राफ कहलाता है, अगर कोई बंद पगडंडी है जिसमें ग्राफ $ G $ का हर किनारा शामिल है। एक यूलर पथ एक ऐसा मार्ग है जो ग्राफ़ के हर किनारे को एक बार उपयोग करता है। एक यूलर पथ विभिन्न सिरों पर शुरू और समाप्त होता है।

एक यूलर सर्किट एक ऐसा सर्किट होता है जो ग्राफ के हर किनारे को एक बार इस्तेमाल करता है। एक यूलर सर्किट हमेशा एक ही शीर्ष पर शुरू और समाप्त होता है। एक जुड़ा हुआ ग्राफ $ G $ एक यूलर ग्राफ है अगर और केवल अगर $ G $ के सभी कोने समान डिग्री के हैं, और एक जुड़ा हुआ ग्राफ $ G $ यूलरियन है और केवल अगर इसका बढ़त सेट चक्र में विघटित हो सकता है।

उपरोक्त ग्राफ $ "a a: a \: 1 \: b \: 2 \: c \: 3 \: d \: 4 \: 4 \: e \: 5 \: c \: 6 \: f \: 7" है। $ g ग्राफ के सभी किनारों को कवर करता है।

हैमिल्टनियन रेखांकन

एक जुड़ा हुआ ग्राफ $ G $ हैमिल्टनियन ग्राफ कहलाता है अगर कोई ऐसा चक्र हो जिसमें $ G $ का हर शीर्ष शामिल हो और चक्र को हैमिल्टनियन चक्र कहा जाता है। ग्राफ $ जी $ में हैमिल्टनियन वॉक एक वॉक है जो प्रत्येक वर्टेक्स से ठीक एक बार गुजरती है।

यदि $ G $ n कोने के साथ एक सरल ग्राफ है, जहाँ $ n \ geq 3 $ if $ deg (v) \ geq \ frac {n} {2} $ प्रत्येक शीर्ष के लिए $ v $ है, तो ग्राफ $ G $ है हैमिल्टन का ग्राफ। यह कहा जाता हैDirac's Theorem।

यदि $ G $ $ n $ वर्टिकल के साथ एक सरल ग्राफ है, जहां $ n \ geq 2 $ यदि $ deg (x) + deg (y) \ geq n $ प्रत्येक जोड़े के लिए गैर-आसन्न कोने x और y है, तो ग्राफ $ G $ हैमिल्टनियन ग्राफ है। यह कहा जाता हैOre's theorem।