असतत गणित - फैला हुआ पेड़
एक जुड़ा हुआ अप्रत्यक्ष ग्राफ $ जी $ का एक फैले हुए वृक्ष एक पेड़ है जिसमें न्यूनतम रूप से $ जी $ के सभी कोने शामिल हैं। एक ग्राफ में कई फैले हुए पेड़ हो सकते हैं।
उदाहरण
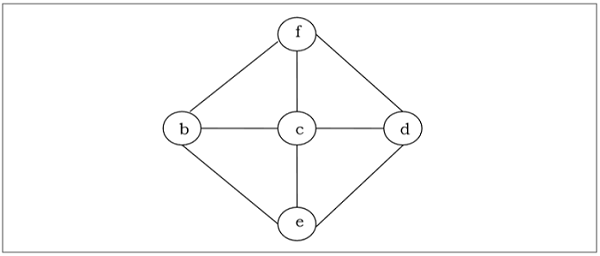
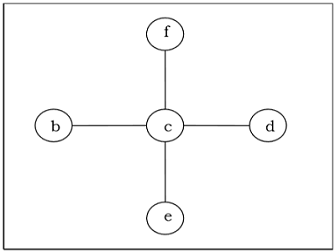
न्यूनतम फैलाव वाला पेड़
एक भारित, जुड़े और अप्रत्यक्ष ग्राफ $ G $ के हर संभव फैले हुए वृक्ष के भार के बराबर या उससे कम भार वाले एक फैले हुए वृक्ष को न्यूनतम फैले हुए वृक्ष (MST) कहा जाता है। एक फैले हुए पेड़ का वजन फैले हुए पेड़ के प्रत्येक किनारे को सौंपे गए सभी भारों का योग है।
उदाहरण
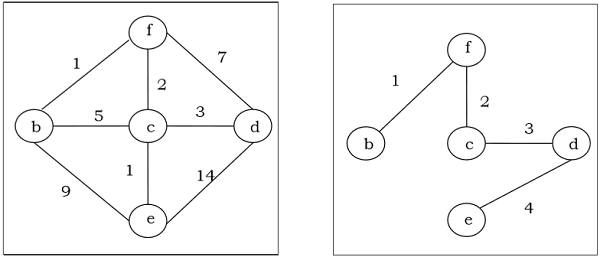
क्रुसकल का एल्गोरिथम
क्रुस्कल का एल्गोरिथ्म एक लालची एल्गोरिथ्म है जो एक जुड़े हुए वेटेड ग्राफ के लिए न्यूनतम फैले हुए पेड़ को ढूंढता है। यह उस ग्राफ के एक पेड़ को ढूँढता है जिसमें हर शिखर शामिल है और पेड़ के सभी किनारों का कुल वजन हर संभव फैले हुए पेड़ से कम या बराबर है।
कलन विधि
Step 1 - दिए गए ग्राफ G (V, E) $ के सभी किनारों को उनके किनारे के वजन के अनुसार आरोही क्रम में व्यवस्थित करें।
Step 2 - ग्राफ से सबसे छोटी वज़न वाली धार चुनें और जांचें कि क्या यह अब तक बने फैले हुए पेड़ के साथ एक चक्र बनाती है।
Step 3 - यदि कोई चक्र नहीं है, तो इस किनारे को फैले हुए पेड़ में शामिल करें और इसे छोड़ दें।
Step 4 - चरण 2 और चरण 3 को तब तक दोहराएं जब तक (V-1) $ किनारों की संख्या फैले हुए पेड़ में नहीं रह जाती।
Problem
मान लीजिए कि हम क्रुस्कल के एल्गोरिथ्म का उपयोग करते हुए निम्नलिखित ग्राफ जी के लिए न्यूनतम फैले हुए पेड़ को खोजना चाहते हैं।
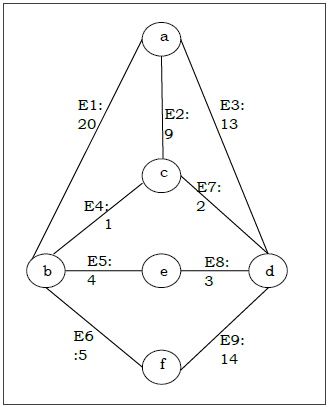
Solution
उपरोक्त ग्राफ से हम निम्नलिखित तालिका बनाते हैं -
| एज नं। | वर्टेक्स जोड़ी | एज वेट |
|---|---|---|
| ई 1 | (ए, बी) | 20 |
| E2 | (एसी) | 9 |
| E3 | (ए, डी) | 13 |
| ई 4 | (बी, सी) | 1 |
| E5 | (बी, ई) | 4 |
| E6 | (बी, एफ) | 5 |
| E7 | (सी, डी) | 2 |
| E8 | (डे) | 3 |
| E9 | (डी, एफ) | 14 |
अब हम एज वज़न के संबंध में तालिका को आरोही क्रम में पुनर्व्यवस्थित करेंगे -
| एज नं। | वर्टेक्स जोड़ी | एज वेट |
|---|---|---|
| ई 4 | (बी, सी) | 1 |
| E7 | (सी, डी) | 2 |
| E8 | (डे) | 3 |
| E5 | (बी, ई) | 4 |
| E6 | (बी, एफ) | 5 |
| E2 | (एसी) | 9 |
| E3 | (ए, डी) | 13 |
| E9 | (डी, एफ) | 14 |
| ई 1 | (ए, बी) | 20 |
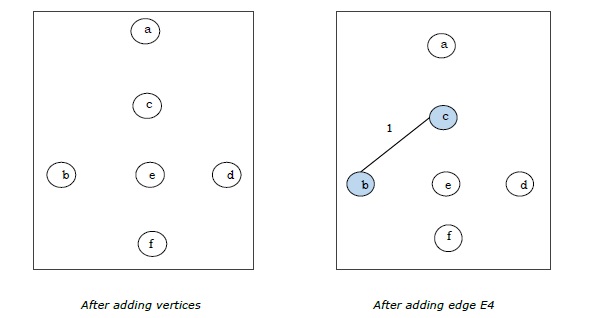
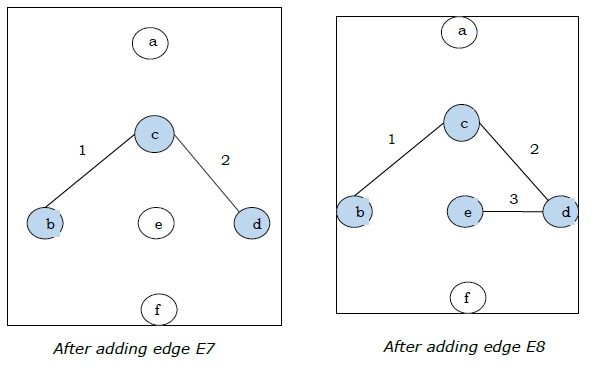
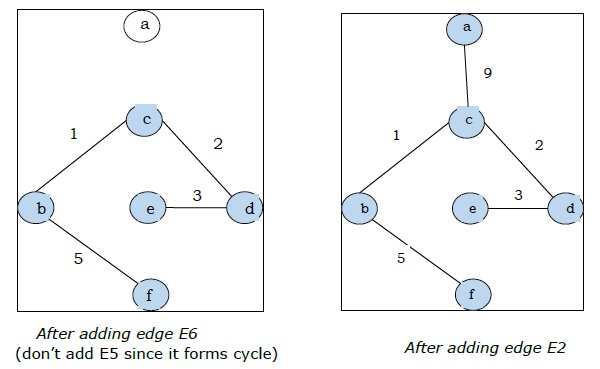
चूँकि हमें अंतिम आकृति में सभी 5 किनारे मिले, हम एल्गोरिथम को रोकते हैं और यह न्यूनतम फैले हुए वृक्ष है और इसका कुल वजन $ (1 + 2 + 3 + 5 + 9) = 20 $ है।
प्राइम का एल्गोरिथम
प्राइमर एल्गोरिथ्म, 1930 में गणितज्ञों, वोजटेक जर्निक और रॉबर्ट सी। प्राइम द्वारा खोजा गया, एक लालची एल्गोरिथ्म है जो एक जुड़े हुए वेटेड ग्राफ के लिए न्यूनतम फैले हुए पेड़ को ढूंढता है। यह उस ग्राफ के एक पेड़ को ढूँढता है जिसमें हर शिखर शामिल है और पेड़ के सभी किनारों का कुल वजन हर संभव फैले हुए पेड़ से कम या बराबर है। प्राइम का एल्गोरिथ्म घने रेखांकन पर तेज है।
कलन विधि
ग्राफ से बेतरतीब ढंग से चुने गए एक एकल शीर्ष के साथ कम से कम फैले हुए पेड़ की शुरुआत करें।
चरण 3 और 4 को दोहराएं जब तक कि सभी कोने पेड़ में शामिल न हो जाएं।
एक किनारे का चयन करें जो पेड़ को एक शीर्ष के साथ जोड़ता है जो अभी तक पेड़ में नहीं है, ताकि किनारे का वजन कम से कम हो और किनारे को शामिल करने से एक चक्र न बने।
चयनित किनारे और शीर्ष जोड़ें जो इसे पेड़ से जोड़ता है।
Problem
मान लीजिए कि हम प्राइम के एल्गोरिथ्म का उपयोग करते हुए निम्नलिखित ग्राफ जी के लिए न्यूनतम फैले हुए पेड़ को ढूंढना चाहते हैं।
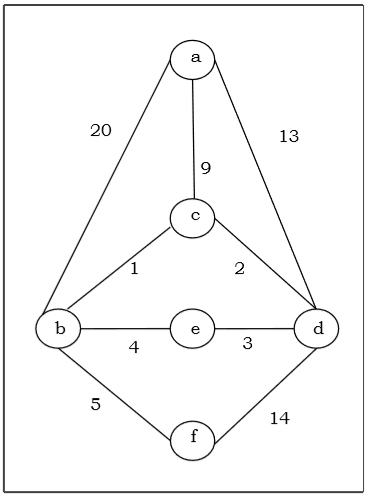
Solution
यहाँ हम 'क' के साथ शुरू करते हैं और आगे बढ़ते हैं।
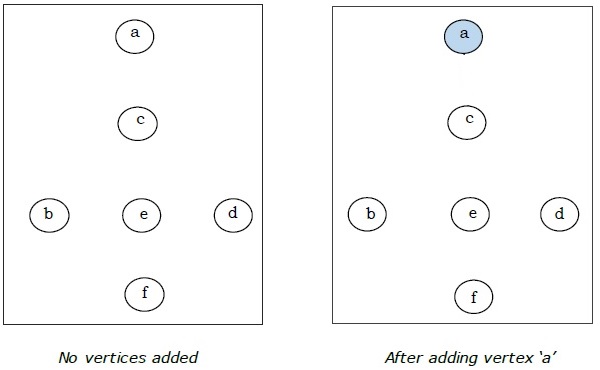
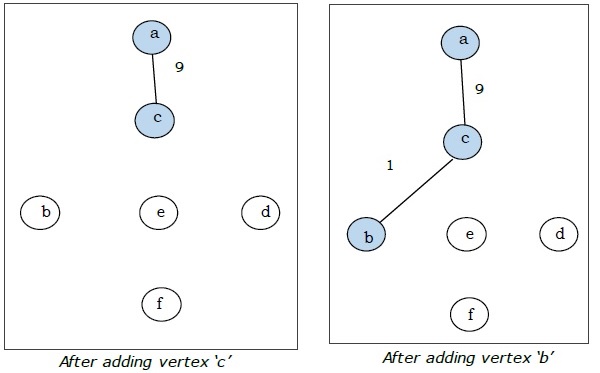
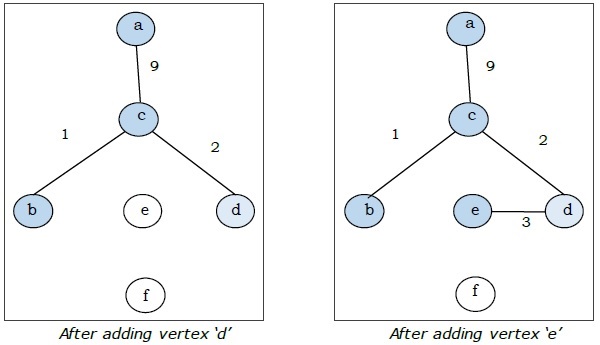
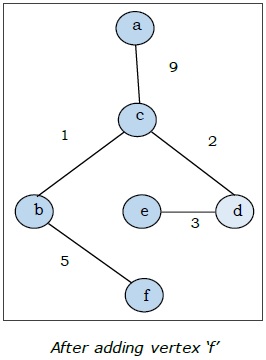
यह न्यूनतम फैले हुए पेड़ है और इसका कुल वजन $ (1 + 2 + 3 + 5 + 9) = 20 $ है।