असतत गणित - समूह
जर्मन गणितज्ञ G. Cantorसेट की अवधारणा शुरू की। उन्होंने एक सेट को कुछ नियमों या विवरणों के माध्यम से चयनित निश्चित और अलग-अलग वस्तुओं के संग्रह के रूप में परिभाषित किया था।
Setसिद्धांत अध्ययन के कई अन्य क्षेत्रों का आधार बनाता है जैसे गिनती सिद्धांत, संबंध, ग्राफ सिद्धांत और परिमित राज्य मशीनें। इस अध्याय में, हम विभिन्न पहलुओं को कवर करेंगेSet Theory।
सेट - परिभाषा
एक सेट विभिन्न तत्वों का एक अनियंत्रित संग्रह है। सेट ब्रैकेट का उपयोग करके इसके तत्वों को सूचीबद्ध करके एक सेट स्पष्ट रूप से लिखा जा सकता है। यदि तत्वों के क्रम को बदल दिया जाता है या सेट के किसी भी तत्व को दोहराया जाता है, तो यह सेट में कोई बदलाव नहीं करता है।
सेट्स के कुछ उदाहरण
- सभी धनात्मक पूर्णांक का एक सेट
- सौरमंडल के सभी ग्रहों का एक समूह
- भारत में सभी राज्यों का एक समूह
- वर्णमाला के सभी निचले अक्षरों का एक सेट
एक सेट का प्रतिनिधित्व
सेट को दो तरीकों से दर्शाया जा सकता है -
- रोस्टर या सारणीबद्ध रूप
- बिल्डर संकेतन सेट करें
रोस्टर या सारणीबद्ध रूप
सेट में सभी तत्वों को सूचीबद्ध करके इसे दर्शाया गया है। तत्वों को ब्रेसिज़ के भीतर संलग्न किया जाता है और कॉमा द्वारा अलग किया जाता है।
Example 1 - अंग्रेजी वर्णमाला में स्वरों का सेट, $ A = \ lbrace a, e, i, o, u \ rbrace $
Example 2 - 10 से कम विषम संख्या का सेट, $ B = \ lbrace 1,3,5,7,9 \ rbrace $
बिल्डर संकेतन सेट करें
सेट को एक संपत्ति को निर्दिष्ट करके परिभाषित किया जाता है जो सेट के तत्वों में आम है। सेट को $ A = \ lbrace x: p (x) \ rbrace $ के रूप में वर्णित किया गया है
Example 1 - सेट $ \ lbrace a, e, i, o, u \ rbrace $ के रूप में लिखा जाता है -
$ A = \ lbrace x: \ text {x अंग्रेजी वर्णमाला में एक स्वर है} \ rbrace $
Example 2 - सेट $ \ lbrace 1,3,5,7,9 \ rbrace $ के रूप में लिखा जाता है -
$ B = \ lbrace x: 1 \ le x \ lt 10 \ और \ (x \% 2) \ ne 0 \ _brace $
यदि कोई तत्व x किसी भी सेट S का सदस्य है, तो इसे S $ में $ x \ _ से दर्शाया जाता है और यदि कोई तत्व y सेट S का सदस्य नहीं है, तो इसे $ y \ notin S $ द्वारा निरूपित किया जाता है।
Example- यदि $ S = \ lbrace1, 1.2, 1.7, 2 \ rbrace, S $ में 1 \
कुछ महत्वपूर्ण सेट
N - सभी प्राकृतिक संख्याओं का सेट = $ \ lbrace1, 2, 3, 4, ..... \ rbrace $
Z - सभी पूर्णांक = $ \ lbrace ....., -3, -2, -1, 0, 1, 2, 3, ..... \ rbrace $ का सेट
Z+ - सभी सकारात्मक पूर्णांकों का सेट
Q - सभी तर्कसंगत संख्याओं का समूह
R - सभी वास्तविक संख्याओं का सेट
W - सभी पूरे नंबरों का सेट
एक सेट की कार्डिनैलिटी
एक सेट S की कार्डिनैलिटी, $ | S | $ द्वारा निरूपित, सेट के तत्वों की संख्या है। संख्या को कार्डिनल संख्या भी कहा जाता है। यदि किसी सेट में तत्वों की अनंत संख्या है, तो इसकी कार्डिनैलिटी $ \ infty $ है।
Example- $ | \ lbrace 1, 4, 3, 5 \ rbrace | = 4, | \ lbrace 1, 2, 3, 4, 5, \ dots \ rbrace | = \ infty $
यदि दो सेट X और Y हैं,
$ | X | = | Y | $ दो सेट X और Y समान कार्डिनैलिटी दर्शाता है। यह तब होता है जब X में तत्वों की संख्या Y में तत्वों की संख्या के बराबर होती है। इस मामले में, X से Y तक एक विशेषण फ़ंक्शन 'f' मौजूद है।
$ | X | \ le | Y | $ यह दर्शाता है कि सेट X की कार्डिनैलिटी, Y की कार्डिनैलिटी से कम या बराबर है। यह तब होता है जब X में तत्वों की संख्या Y के बराबर या उससे कम होती है। यहां, X से Y तक एक इंजेक्शन फ़ंक्शन 'f' मौजूद है।
$ | X | \ lt | Y | $ यह दर्शाता है कि सेट X की कार्डिनैलिटी, Y की कार्डिनैलिटी से कम है। यह तब होता है जब X में तत्वों की संख्या Y से कम होती है। यहाँ, X से Y तक फ़ंक्शन 'f' इंजेक्शन फ़ंक्शन है, लेकिन विशेषण नहीं है।
$ If \ | X | \ ले | Y | $ और $ | X | \ ge | Y | $ तब $ | X | = | वाई | $ सेट X और Y को सामान्यतः समान सेट के रूप में जाना जाता है।
सेट के प्रकार
सेटों को कई प्रकारों में वर्गीकृत किया जा सकता है। जिनमें से कुछ परिमित, अनंत, सबसेट, सार्वभौमिक, उचित, सिंगलटन सेट आदि हैं।
परिमित सेट
एक सेट जिसमें तत्वों की निश्चित संख्या होती है, एक परिमित सेट कहलाता है।
Example- $ S = \ lbrace x \: | \ N में $ x और $ 70 \ gt x \ gt 50% rbrace $
अनंत सेट
एक सेट जिसमें अनंत संख्या में तत्व होते हैं उसे अनंत सेट कहा जाता है।
Example- $ S = \ lbrace x \: | \ N में $ x और $ x \ gt 10 \ rbrace $
सबसेट
एक सेट X सेट Y का एक उपसमूह है ($ X \ subseteq Y $ के रूप में लिखा गया है) यदि X का प्रत्येक तत्व सेट Y का एक तत्व है।
Example 1- चलो, $ X = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ और $ Y = \ lbrace 1, 2 \ rbrace $। यहाँ सेट Y सेट X का एक सबसेट है क्योंकि सेट Y के सभी तत्व X में सेट है। इसलिए, हम $ Y \ subseteq X $ लिख सकते हैं।
Example 2- चलो, $ X = \ lbrace 1, 2, 3 \ rbrace $ और $ Y = \ lbrace 1, 2, 3 \ rbrace $। यहाँ सेट Y, सेट X का एक सबसेट (उचित उपसमूह नहीं) है क्योंकि सेट Y के सभी तत्व सेट X में है। इसलिए, हम $ Y \ subseteq X $ लिख सकते हैं।
उचित सबसेट
शब्द "उचित सबसेट" को "सबसेट नहीं बल्कि बराबर" के रूप में परिभाषित किया जा सकता है। एक सेट X सेट Y का एक उचित उपसमूह है ($ X \ subset Y $ के रूप में लिखा गया है) यदि X का प्रत्येक तत्व सेट Y और $ X का एक तत्व है। \ lt | Y | $।
Example- चलो, $ X = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ और $ Y = \ lbrace 1, 2 \ rbrace $। यहाँ $ Y \ सब्सेट X $ को सेट करें क्योंकि $ Y $ में सभी तत्व $ X $ में भी समाहित हैं और $ X में कम से कम एक तत्व सेट $ Y $ से अधिक है।
सार्वसमुच्चय
यह किसी विशेष संदर्भ या अनुप्रयोग में सभी तत्वों का एक संग्रह है। उस संदर्भ या अनुप्रयोग के सभी सेट अनिवार्य रूप से इस सार्वभौमिक सेट के सबसेट हैं। यूनिवर्सल सेट को $ U $ के रूप में दर्शाया गया है।
Example- हम पृथ्वी पर सभी जानवरों के सेट के रूप में $ U $ को परिभाषित कर सकते हैं। इस मामले में, सभी स्तनधारियों का सेट $ U $ का सबसेट है, सभी मछलियों का सेट $ U $ का सबसेट है, सभी कीड़ों का सेट $ U $ का सबसेट है, और इसी तरह।
खाली सेट या अशक्त सेट
एक खाली सेट में कोई तत्व नहीं होते हैं। इसे $ \ emptyset $ द्वारा दर्शाया गया है। जैसे खाली सेट में तत्वों की संख्या परिमित होती है, वैसे ही खाली सेट एक परिमित सेट होता है। खाली सेट या अशक्त सेट की कार्डिनैलिटी शून्य है।
Example- $ S = \ lbrace x \: | \ N और $ 7 में $ \ x \ lt x \ lt 8 \ rbrace = \ emptyset $
सिंगलटन सेट या यूनिट सेट
सिंगलटन सेट या यूनिट सेट में केवल एक तत्व होता है। एक सिंगलटन सेट को $ lbrace s \ rbrace $ द्वारा दर्शाया गया है।
Example- $ S = \ lbrace x \: | \ N में \ "x \", \ 7 \ lt x \ lt 9 \ rbrace $ = $ \ lbrace 8 \ _bbrace $
समान सेट
यदि दो सेटों में समान तत्व होते हैं तो उन्हें समान कहा जाता है।
Example - यदि $ A = \ lbrace 1, 2, 6 \ rbrace $ और $ B = \ lbrace 6, 1, 2 \ rbrace $, वे समान हैं क्योंकि सेट A का प्रत्येक तत्व सेट B का एक तत्व है और सेट का प्रत्येक तत्व है। B, A का एक तत्व है।
समतुल्य सेट
यदि दो सेटों की कार्डिनैलिटी समान हैं, तो उन्हें समकक्ष सेट कहा जाता है।
Example- यदि $ A = \ lbrace 1, 2, 6 \ rbrace $ और $ B = \ lbrace 16, 17, 22 \ rbrace $, तो वे समान हैं क्योंकि A की कार्डिनैलिटी B. की समानता के बराबर है - $ / A | = | बी | = 3 $
ओवरलैपिंग सेट
कम से कम एक सामान्य तत्व वाले दो सेटों को ओवरलैपिंग सेट कहा जाता है।
ओवरलैपिंग सेट के मामले में -
$ n (A \ cup B) = n (A) + n (B) - n (A \ cap B) $
$ n (A \ cup B) = n (A - B) + n (B - A) + n (A \ cap B) $
$ n (ए) = एन (ए - बी) + एन (ए \ कैप बी) $
$ n (B) = n (B - A) + n (A \ cap B) $
Example- चलो, $ A = \ lbrace 1, 2, 6 \ rbrace $ और $ B = \ lbrace 6, 12, 42 \ rbrace $। एक सामान्य तत्व '6' है, इसलिए ये सेट ओवरलैपिंग सेट हैं।
सेट को खारिज करें
दो सेट ए और बी को डिसऑइंटर्स सेट कहा जाता है यदि उनके पास एक तत्व भी नहीं है। इसलिए, disjoint सेट के निम्नलिखित गुण हैं -
$ n (A \ cap B) = \ emptyset $
$ n (A \ cup B) = n (A) + n (B) $
Example - चलो, $ A = \ lbrace 1, 2, 6 \ rbrace $ और $ B = \ lbrace 7, 9, 14 \ rbrace $, एक भी सामान्य तत्व नहीं है, इसलिए ये सेट ओवरलैपिंग सेट हैं।
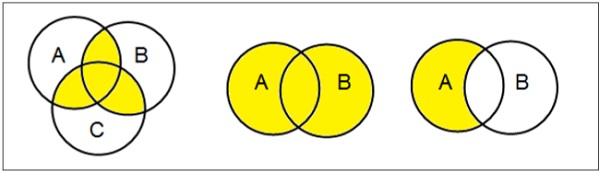
वेन डायग्राम
जॉन वेन द्वारा 1880 में आविष्कार किया गया वेन आरेख, एक योजनाबद्ध आरेख है जो विभिन्न गणितीय सेटों के बीच सभी संभावित तार्किक संबंधों को दर्शाता है।
Examples
संचालन सेट करें
सेट ऑपरेशंस में सेट यूनियन, सेट इन्टरसेक्शन, सेट डिफरेंस, सेट का पूरक और कार्टेशियन प्रोडक्ट शामिल हैं।
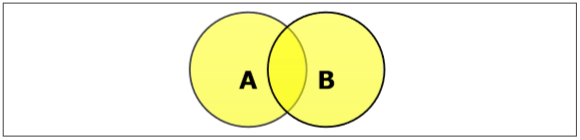
यूनियन सेट करें
सेट ए और बी का संघटन ($ A \ कप B $ द्वारा निरूपित) तत्वों का समूह है जो A, B, या A और B दोनों में हैं। इसलिए, $ A \ कप B = \ lbrace x \: | B \ rbrace $ में A \ OR \ x \ में \ \ x।
Example- यदि $ A = \ lbrace 10, 11, 12, 13 \ rbrace $ और B = $ \ lbrace 13, 14, 15 \ rbrace $, तो $ A \ कप B = \ lbrace 10, 11, 12, 13, 14 , 15 \ rbrace $। (सामान्य तत्व केवल एक बार होता है)
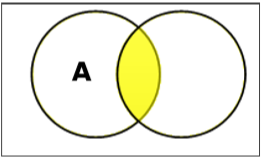
अंतःकरण सेट करें
सेट A और B का प्रतिच्छेदन ($ A \ cap B $ द्वारा निरूपित किया जाता है) तत्वों का समूह है जो A और B दोनों में हैं। इसलिए $ A \ cap B = \ lbrace x \: | \: x \ A में B \ rbrace $ में \ AND \ x \
Example - यदि $ A = \ lbrace 11, 12, 13 \ rbrace $ और $ B = \ lbrace 13, 14, 15 \ rbrace $, तो $ A \ cap B = \ lbrace 13 \ rbrace $।
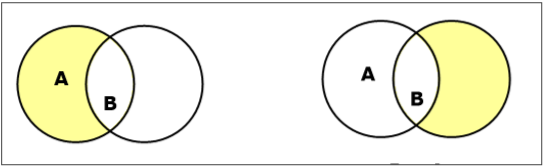
अंतर / सापेक्ष पूरक सेट करें
सेट ए और बी का सेट अंतर ($ A - B $ द्वारा निरूपित) उन तत्वों का समूह है जो केवल A में हैं लेकिन B. में नहीं हैं। इसलिए, $ A - B = \ lbrace x \: | $ \ _ \ _ ए \ एंड \ में \ बी बी \ rbrace $।
Example- यदि $ A = \ lbrace 10, 11, 12, 13 \ rbrace $ और $ B = \ lbrace 13, 14, 15 \ rbrace $, तो $ (A - B) = \ lbrace 10, 11, 12 \ rbrace $ और $ (B - A) = \ lbrace 14, 15 \ rbrace $। यहाँ, हम $ (A - B) \ ne (B - A) $ देख सकते हैं
एक सेट के पूरक
एक सेट ए का पूरक ($ ए '$ द्वारा निरूपित) उन तत्वों का सेट है जो सेट ए में नहीं हैं। इसलिए, $ ए' = \ lbrace x | x \ not $ A \ rbrace $।
अधिक विशेष रूप से, $ A '= (U - A) $ जहां $ U $ एक सार्वभौमिक सेट है जिसमें सभी ऑब्जेक्ट होते हैं।
Example- यदि $ ए = \ lbrace x \: | \ "x \ \: {अंतर्गत \ _: \: सेट \: की \: विषम \: पूर्णांक} \ rbrace $ तब $ A '= \ lbrace y \: | \ \ y \ \: {क्या \ _: \: नहीं \: संबंधित:: \: सेट \: का \: विषम \: पूर्णांक} \ rbrace $

कार्तीय उत्पाद / क्रॉस उत्पाद
के सेट की संख्या का कार्टेशियन उत्पाद $ A_1, A_2, \ dots A_n $ को $ A_1 के रूप में दर्शाया गया है A_2 \ dots \ टाइम्स A_n $ को सभी संभव ऑर्डर किए गए जोड़े के रूप में परिभाषित किया जा सकता है (x_1, x_2, \ dots x_n) $ जहाँ $ x_1 \ _ A_1 में, x_2 \ A_2 में, \ dots x_n \ A_n $ में
Example - अगर हम दो सेट लेते हैं $ A = \ lbrace a, b \ rbrace $ और $ B = \ lbrace 1, 2 \ rbrace $
A और B का कार्टेशियन उत्पाद इस रूप में लिखा गया है - $ A \ बार B = \ lbrace (a, 1), (a, 2), (b, 1), (b, 2) \ rbrace $
B और A का कार्टेशियन उत्पाद इस प्रकार लिखा गया है - $ B \ टाइम्स A = \ lbrace (1, a), (1, b), (2, a), (2, b) \ rbrace $
सत्ता स्थापित
एक सेट S का पावर सेट खाली सेट सहित S के सभी सबसेट का सेट है। कार्डिनलिटी n के सेट S के एक पावर सेट की कार्डिनैलिटी $ 2 ^ n $ है। पावर सेट को $ P (S) $ के रूप में दर्शाया गया है।
Example −
एक सेट $ S = \ lbrace a, b, c, d \ rbrace $ के लिए हम सबसेट की गणना करते हैं -
0 तत्वों के साथ ग्राहकी - $ \ lbrace \ emptyset \ rbrace $ (खाली सेट)
1 तत्व वाले सब्स्क्रिप्शन - $ \ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace c \ rbrace, \ lbrace d \ rbrace $
2 तत्वों वाले सब्स्क्रिप्शन - $ \ lbrace a, b \ rbrace, \ lbrace a, c \ rbrace, \ lbrace a, d \ rbrace, \ lbrace b, c \ rbrace, \ lbrace b, d \ rbrace, \ lbrace c, d \ rbrace $
3 तत्वों वाले सब्सक्रिप्शन - $ \ lbrace a, b, c \ rbrace, \ lbrace a, b, d \ rbrace, \ lbrace a, c, d \ rbrace, \ lbrace b, c, d \ rbrace $
4 तत्वों वाले सब्स्क्रिप्शन - $ \ lbrace a, b, c, d \ rbrace $
इसलिए, $ P (S) = $
$ \ _ \ _ \ _ \ _ \ _ \ n rbrace, \ lbrace a, d \ rbrace, \ lbrace b, c \ rbrace, \ lbrace b, d \ rbrace, \ lbrace c, d \ rbrace, \ lbrace a, b, c \ rbrace, \ lbrace a, b, b d \ rbrace, \ lbrace a, c, d \ rbrace, \ lbrace b, c, d \ rbrace, \ lbrace a, b, c, d \ rbrace \ quad \ rbrace $
$ | पी (एस) | = 2 ^ 4 = 16 $
Note - खाली सेट का पावर सेट भी एक खाली सेट है।
$ | पी (\ lbrace \ emptyset \ rbrace) | = 2 ^ 0 = 1 $
एक सेट का विभाजन
S का कहना है कि एक सेट का विभाजन , n डिसइंटर्स सब्मिट का एक संग्रह है , $ P_1, P_2, \ Dots P_n $ का कहना है जो निम्नलिखित तीन स्थितियों को संतुष्ट करता है -
$ P_i $ में खाली सेट नहीं है।
$ \ lbrack P_i \ ne \ lbrace \ emptyset \ rbrace \ for \ all \ 0 \ lt i \ le n \ rbrack $
सबसेट का संघ पूरे मूल सेट के बराबर होना चाहिए।
$ \ lbrack P_1 \ cup P_2 \ cup \ dots \ cup P_n = S \ rbrack $
किन्हीं दो अलग-अलग सेटों का अंतरच्छेदन खाली है।
$ \ lbrack P_a \ cap P_b = \ lbrace \ emptyset \ rbrace, \ for \ a \ ne b \ जहाँ \ n \ ge a, \: b \ ge 0 \ rbrack $
Example
$ S = \ lbrace a, b, c, d, e, f, g, h \ rbrace $
एक संभावित विभाजन $ \ lbrace a \ rbrace, \ lbrace b, c, d \ rbrace, \ lbrace e, f, g, h \ rbrace $ है
एक और संभावित विभाजन $ \ lbrace a, b \ rbrace, \ lbrace c, d \ rbrace, \ lbrace e, f, g, h \ rbrace $ है
बेल नंबर
बेल नंबर एक सेट को विभाजित करने के तरीकों की संख्या की गिनती देते हैं। उन्हें $ B_n $ द्वारा निरूपित किया जाता है जहां n सेट की कार्डिनैलिटी है।
Example -
$ S = \ lbrace 1, 2, 3 \ rbrace $, $ n = S | = 3 $
वैकल्पिक विभाजन हैं -
1. $ \ emptyset, \ lbrace 1, 2, 3 \ rbrace $
2. $ \ lbrace 1 \ rbrace, \ lbrace 2, 3 \ rbrace $
3. $ \ lbrace 1, 2 \ rbrace, \ lbrace 3 \ rbrace $
4. $ \ lbrace 1, 3 \ rbrace, \ lbrace 2 \ rbrace $
5. $ \ lbrace 1 \ rbrace, \ lbrace 2 \ rbrace, \ lbrace 3 \ rbrace $
इसलिए $ B_3 = 5 $