रीजनिंग - कोडेड बाइनरी नंबर
जिस संख्या में आधार 2 है उसे बाइनरी नंबर के रूप में जाना जाता है। बाइनरी नंबर 0 और 1 के पूरक द्वारा बनाया गया है। तो, कोडित बाइनरी नंबर में दो प्रक्रियाएं होती हैं। एक द्विआधारी का दशमलव में रूपांतरण है और दूसरा दशमलव में द्विआधारी है।
दशमलव संख्याएं
क्या जानना है binary number, पहले हमें दशमलव संख्याओं के बारे में जानना होगा। तो, दशमलव संख्या में दस अंक (अर्थात 0,1,2,3,4,5,6,7,8,9) होते हैं। इन संख्याओं का उपयोग करके किसी भी दशमलव प्रणाली का प्रतिनिधित्व किया जा सकता है। उदाहरण के लिए, अंकों का एक क्रम 2, 4, 6 है और 8. हम इसे निम्नलिखित तरीके से करते हैं -
2468 = 2 × 10 3 + 4 × 10 2 + 6 × 10 1 + 8 × 10 0
= 2468
Note- हम इस मामले में संख्याओं के मूल्य को 10 की शक्तियों द्वारा अनुक्रम के विभिन्न अंकों को गुणा करके और जोड़कर प्राप्त करते हैं। यहाँ इस 10 को आधार या मूलांक कहा जाता है। इसलिए एक दशमलव प्रणाली के तहत हमारा आधार 10 है।
बाइनरी नंबर
हम एक का प्रतिनिधित्व करने के लिए दस अंकों का उपयोग करते हैं decimal number; जैसे कि हम द्विआधारी संख्या का प्रतिनिधित्व करने के लिए केवल दो अंकों का उपयोग करते हैं। इन दो अंकों यानी 0 और 1 का उपयोग करके किसी भी संख्या का प्रतिनिधित्व किया जा सकता है।
एक द्विआधारी संख्या का उदाहरण है- 1101. यहां 4 अंक अंकों के अनुक्रम में मौजूद हैं - 1, 1, 0, 1. हम निम्नलिखित तरीके से मूल्य प्राप्त करते हैं।
1101 = 1 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0
= 8 + 4 + 0 + 1 = 13
इस प्रकार, द्विआधारी संख्या दशमलव प्रणाली में तेरह का प्रतिनिधित्व करती है। मूल्य द्वारा निर्धारित किया जा सकता हैmultiplying different digits 2 और जोड़ने की शक्तियों द्वारा अनुक्रम का।
Conventional method - उपरोक्त उदाहरण में, हम देखते हैं कि किसी भी बाइनरी नंबर का मान पाने के लिए, हम निम्नलिखित नियम का उपयोग करते हैं -
दाएं से पहला अंक 2 0 = 1 से गुणा किया जाता है
दाएं से दूसरा अंक 2 1 = 2 से गुणा किया जाता है
दाईं ओर से तीसरा अंक 2 2 = 4 से गुणा किया जाता है
इसी तरह, दाईं ओर से n वें अंक को 2 n from 1 से गुणा किया जाता है
अंत में, इन सभी को जोड़ा जाता है।
For Example - निम्नलिखित बाइनरी संख्याओं को दशमलव संख्याओं में परिवर्तित करें।
A - 1010
B - 1111
C - 100
D - 10000
Solution -
ए - 1010 = 1 × 2 3 + 0 × 2 2 + 1 × 2 1 + 0 × 2 0
बी - 1111 = 1 × 2 3 + 1 × 2 2 + 1 × 2 1 + 1 × 2 0
सी - 100 = 1 × 2 2 + 0 × 2 1 + 0 × 2 0
डी - 10000 = 1 × 2 4 + 0 × 2 3 + 0 × 2 2 + 0 × 2 1 + 0 × 2 0
शीघ्र विधि
Step I- दी गई संख्या के सही अंक से शुरू करके, 1, 2, 4, 8, 16, 32 …… लिखिए। और जैसा कि आप बाईं ओर जाते हैं, प्रत्येक अंक के नीचे।
Step II- 0 से नीचे के नंबरों को इग्नोर करें। 1s नीचे सभी संख्याओं को जोड़ें।
आइए इस विधि द्वारा उदाहरण 1 को हल करें।
A - 1010
हम 1,2,4,8 का उपयोग करेंगे क्योंकि यहाँ 4 अंक मौजूद हैं।
हमें मिला,
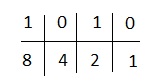
4 और 1 शून्य से नीचे आते हैं। हम उन्हें अनदेखा करते हैं और शेष जोड़ते हैं। हमें 8 + 2 = 10 मिलता है
इस तरह हम अन्य संख्याओं को हल कर सकते हैं।
दशमलव संख्या को बाइनरी में परिवर्तित किया जा सकता है successive divisions। विभाजन के हर बार, लाभांश को 2 से विभाजित किया जाता है। अनुस्मारक को नोट किया जाता है और भागफल अगला लाभांश बन जाता है, जिसे फिर से 2 से विभाजित किया जाता है। प्रक्रिया तब तक दोहराई जाती है जब तक कोई और विभाजन संभव नहीं होता।
उदाहरण के लिए - 17 को बाइनरी नंबर में बदलें -
17 को 2 से विभाजित करें जब तक कोई अधिक विभाजन संभव नहीं है।
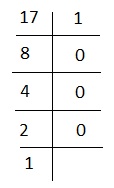
तो, 17 का बाइनरी फॉर्म 10001 है।
Direction (Q. 1-4) − Study the following question and give the answer.
एक निश्चित कोड में, 0 के लिए प्रतीक + है और 1 के लिए # है। कोई संख्या या प्रतीक 1. से अधिक नहीं है। 1 के लिए प्रतीक का मूल्य हर बार जब वह एक जगह को बाईं ओर शिफ्ट करता है।
'0' को + के रूप में दर्शाया गया है
'1' को # के रूप में दर्शाया गया है
'2' को # + के रूप में दर्शाया गया है
# 3 को ## के रूप में दर्शाया गया है
'4' को # ++ और इतने पर दर्शाया गया है
1 - निम्नलिखित में से कौन 11 का प्रतिनिधित्व करेगा?
Options -
A - # + ##
B - + ## +
C - ## ++
D - # + # ++
E - इनमें से कोई नहीं
Answer - विकल्प A
Explanation - 11 के बराबर पाने के लिए, हम 2 द्वारा क्रमिक विभाजन की विधि का उपयोग करते हैं।

तो बाइनरी फॉर्म 10111 होगा। 1 और 0 की जगह # और + हमें # + ## मिलेगा।
2 - निम्न में से कौन 8 का प्रतिनिधित्व करेगा?
Options -
A - ## ++
B - + ## +
C - ## ++
D - ++ ##
E - इनमें से कोई नहीं
Answer - विकल्प ई
Explanation - 8 के लिए, हमारे पास है-
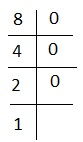
यानी 1000 या # +++। सही विकल्प 5 है।
3 - ## + # द्वारा निम्नलिखित में से किसका प्रतिनिधित्व किया जाएगा?
Options -
A - 8
B - 1 1
C - 13
D - 12
E - इनमें से कोई नहीं
Answer - विकल्प ई
Explanation- ## + # = 1101 = 1 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0 0 = 15
4 - निम्नलिखित में से कौन सी संख्या # +++ # द्वारा दर्शाई जाएगी?
Options -
A - 22
B - 31
C - 14
D - 17
E - इनमें से कोई नहीं
Answer - विकल्प डी
Explanation - # + + + # = 10001
= 1 × 2 4 + 0 × 2 3 + 0 × 2 2 + 0 × 2 1 + 1 × 2 0
= 16 + 1 = 17
बाइनरी सिस्टम में आधार 2 होता है, एक दशमलव प्रणाली का आधार 10 होता है, और तृतीयक प्रणाली का आधार 3 होता है, जबकि अष्टक प्रणाली का आधार 8. होता है। तृतीयक के मामले में, संख्याओं का प्रतिनिधित्व करने के लिए हमारे पास तीन अंक होते हैं। ये 0, 1 और 2 हैं। इस मामले में संख्याओं को 3 की उपयुक्त शक्तियों के साथ गुणा करके दशमलव में परिवर्तित किया जाएगा।
For Example -
(12012) 3 = 1 × 3 4 + 2 × 3 3 + 0 × 3 2 + 1 × 3 1 + 2 × 3 0 = (104) 3