तर्क - तर्कपूर्ण कटौती
तार्किक कटौती एक महत्वपूर्ण अध्याय है क्योंकि इस अध्याय से कई आसान और अंक लाने वाले प्रश्न विभिन्न प्रतियोगी परीक्षाओं में शामिल किए जाते हैं। इस अध्याय में, हम ऐसी समस्याओं को हल करने के लिए दो तरीकों पर चर्चा करेंगे -
- सिलोलिज़्म विधि
- वेन आरेख विधि
मूल बातें
यदि दो कथन हैं, तो समस्या को हल करने का सबसे अच्छा तरीका होगा, लेकिन अगर बयान की संख्या दो से अधिक है, तो वेन आरेख विधि के लिए जाएं। कभी-कभी बयान और निष्कर्ष सामान्य स्वीकृत तथ्यों से प्राप्त होते हैं लेकिन वे भी गैर तार्किक हो सकते हैं। उदाहरण के लिए -
a) कुछ कुर्सियाँ दरवाजे हैं।
b) सभी पुरुष महिला हैं
c) कोई दूध सफेद नहीं है
निष्कर्ष पर पहुंचने के लिए, अमूर्त सोच की आवश्यकता होती है। एक वाक्य की तार्किक समझ को समझने की जरूरत है फिर उसके अनुसार निष्कर्ष का जवाब देना होगा। प्रत्येक कथन को सत्य के रूप में सोचने की आवश्यकता है, फिर हमें यह सत्यापित करना होगा कि क्या निष्कर्ष तार्किक रूप से कथन का अनुसरण कर रहे हैं।
क्वालिफायर
ये कुछ ऐसे प्राथमिक शब्द हैं, जिनका उपयोग यह बताने के लिए किया जाता है कि एक चीज एक जैसी या दूसरी से कितनी अलग है। कुछ क्वालीफायर का उदाहरण "ऑल", "कुछ", "कुछ-नहीं" आदि हैं।
वेन आरेख अवधारणा
दूसरी ओर, वेन आरेख एक प्रक्रिया है जहां हम ज्यामितीय आंकड़ों के रूप में एक वाक्य या कथन का प्रतिनिधित्व कर सकते हैं। सभी दिए गए बयान संभव वेन आरेखों में दिए गए हैं। फिर सभी निष्कर्ष उन आरेखों के साथ सत्यापित किए जाते हैं। कोई भी निष्कर्ष जो सभी वेन आरेखों को संतुष्ट करता है उसे एक वैध निष्कर्ष माना जाएगा।
| बयान | पत्राचार वेन आरेख |
|---|---|
| सभी A, B हैं |
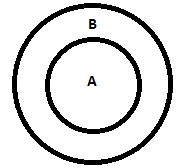
|
| कुछ A B (OR) हैं तो कुछ A B नहीं हैं |
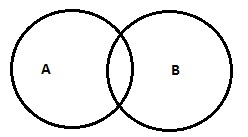
|
| नहीं ए बी है |
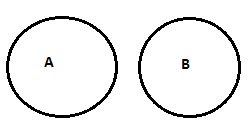
|
आइए इसे बेहतर तरीके से समझने के लिए एक सरल उदाहरण लेते हैं।
Sample − 1
Statements -
सभी इंजीनियर मूर्ख हैं। सभी मूर्ख डॉक्टर हैं। सभी डॉक्टर गरीब हैं।
Conclusions -
I. कुछ गरीब मूर्ख हैं।
द्वितीय। कुछ गरीब इंजीनियर हैं।
Options -
A - केवल मैं ही मान्य हूं
B - केवल II ही मान्य है
C - दोनों कथन मान्य हैं
D - कोई भी कथन मान्य नहीं है
Answer - विकल्प सी
Explanation -
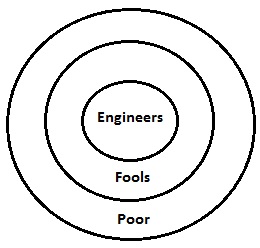
दिए गए कथनों के लिए Venn आरेख ऊपर खींचा गया है। यह एक जगह पर आरेखीय रूप से सभी कथनों को दर्शाता है। यहां अब अगर हम एक-एक करके निष्कर्षों के बारे में चर्चा करेंगे, तो सब कुछ स्पष्ट हो जाएगा।
यहां मूर्ख गरीबों के सबसेट हैं। तो यह एक स्पष्ट तथ्य है कि कुछ गरीब मूर्ख होंगे। इसलिए, निष्कर्ष I मान्य है। इसी तरह निष्कर्ष II मान्य है क्योंकि इंजीनियर भी गरीबों के सबसेट हैं। अत: दोनों कथन मान्य होंगे।
Sample − 2
Statements -
कुछ कीबोर्ड माउस हैं। कुछ माउस रेडियो हैं।
Conclusions -
I. कुछ कीबोर्ड रेडियो हैं।
द्वितीय। कुछ रेडियो कीबोर्ड हैं
तृतीय। सभी रेडियो माउस हैं।
चतुर्थ। सभी माउस कीबोर्ड हैं।
Options -
A - केवल निष्कर्ष I मान्य है
B - केवल निष्कर्ष II ही मान्य है
C - या तो I या II वैध है
D - कोई भी निष्कर्ष मान्य नहीं है
E - दोनों और II मान्य हैं
Answer - विकल्प डी
Explanation - चूंकि दोनों कथन विशेष हैं, कोई निश्चित निष्कर्ष मान्य नहीं है।
Sample − 3
Statements -
सभी छात्र शांत हैं। सभी छात्र शरारती हैं।
Conclusions -
I. सभी शरारती या तो शांत हैं या इसके विपरीत।
द्वितीय। कुछ शांत व्यक्ति शरारती हैं।
तृतीय। आम तौर पर शरारती शांत होते हैं।
चतुर्थ। अपराध और अपराधबोध एक साथ चलते हैं।
Options -
A - केवल निष्कर्ष I मान्य है
B - केवल निष्कर्ष II ही मान्य है
C - या तो I या II वैध है
D - I या II में से कोई भी मान्य नहीं है
E - दोनों और II मान्य हैं
Answer - विकल्प बी
Explanation- चूंकि मध्यवर्ती शब्द 'छात्रों' को बयानों में दो बार वितरित किया जाता है, इसलिए निष्कर्ष व्यापक नहीं हो सकता है। इसलिए, यह मान्य है कि 'कुछ शांत व्यक्ति शरारती हैं'। इस प्रकार, II सत्य है।