DAA - Biner Heap
Ada beberapa jenis heap, namun pada bab ini kita akan membahas heap biner. SEBUAHbinary heapadalah struktur data, yang terlihat mirip dengan pohon biner lengkap. Struktur data heap mematuhi properti pengurutan yang dibahas di bawah ini. Umumnya, Heap diwakili oleh sebuah array. Dalam bab ini, kami merepresentasikan heap olehH.
Karena elemen heap disimpan dalam array, dengan mempertimbangkan indeks awal sebagai 1, posisi simpul induk dari ith elemen dapat ditemukan di ⌊ i/2 ⌋. Anak kiri dan anak kananith node berada di posisi 2i dan 2i + 1.
Heap biner dapat diklasifikasikan lebih lanjut sebagai a max-heap atau a min-heap berdasarkan properti pemesanan.
Max-Heap
Di heap ini, nilai kunci node lebih besar dari atau sama dengan nilai kunci turunan tertinggi.
Karenanya, H[Parent(i)] ≥ H[i]
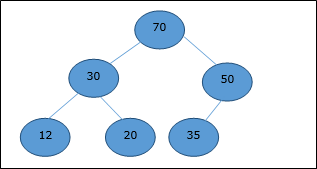
Min-Heap
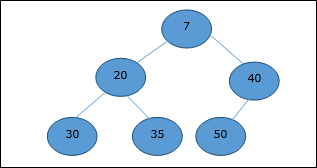
Dalam mean-heap, nilai kunci sebuah node lebih kecil dari atau sama dengan nilai kunci dari turunan terendah.
Karenanya, H[Parent(i)] ≤ H[i]
Dalam konteks ini, operasi dasar ditunjukkan di bawah ini sehubungan dengan Max-Heap. Penyisipan dan penghapusan elemen di dalam dan dari heaps membutuhkan penataan ulang elemen. Karenanya,Heapify fungsi perlu dipanggil.
Representasi Array
Pohon biner lengkap dapat diwakili oleh larik, menyimpan elemennya menggunakan traversal urutan tingkat.
Mari kita pertimbangkan heap (seperti yang ditunjukkan di bawah) yang akan diwakili oleh sebuah array H.
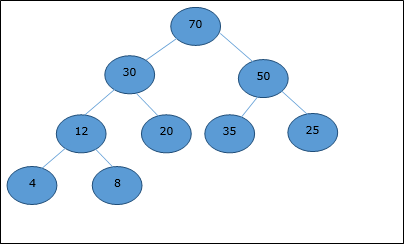
Mempertimbangkan indeks awal sebagai 0, dengan menggunakan traversal urutan tingkat, elemen disimpan dalam larik sebagai berikut.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... |
| elements | 70 | 30 | 50 | 12 | 20 | 35 | 25 | 4 | 8 | ... |
Dalam konteks ini, operasi pada heap direpresentasikan sehubungan dengan Max-Heap.
Untuk menemukan indeks induk dari suatu elemen pada indeks i, algoritma berikut Parent (numbers[], i) digunakan.
Algorithm: Parent (numbers[], i)
if i == 1
return NULL
else
[i / 2]Indeks anak kiri dari sebuah elemen di index i dapat ditemukan menggunakan algoritma berikut, Left-Child (numbers[], i).
Algorithm: Left-Child (numbers[], i)
If 2 * i ≤ heapsize
return [2 * i]
else
return NULLIndeks anak kanan dari sebuah elemen di indeks i dapat ditemukan menggunakan algoritma berikut, Right-Child(numbers[], i).
Algorithm: Right-Child (numbers[], i)
if 2 * i < heapsize
return [2 * i + 1]
else
return NULL