DAA - Grafik Multistage
Grafik bertingkat G = (V, E) adalah grafik berarah tempat simpul dipartisi k (dimana k > 1) jumlah subset yang terputus-putus S = {s1,s2,…,sk}sehingga tepi (u, v) ada di E, lalu u s i dan v Є s 1 + 1 untuk beberapa subset di partisi dan |s1| = |sk| = 1.
Titik puncak s Є s1 disebut source dan puncak t Є sk disebut sink.
Gbiasanya diasumsikan sebagai grafik berbobot. Dalam grafik ini, biaya sebuah sisi (i, j) diwakili oleh c (i, j) . Oleh karena itu, biaya jalur dari sumbers tenggelam t adalah jumlah biaya dari setiap sisi di jalur ini.
Masalah grafik bertingkat adalah menemukan jalur dengan biaya minimum dari sumber s tenggelam t.
Contoh
Perhatikan contoh berikut untuk memahami konsep grafik bertingkat.
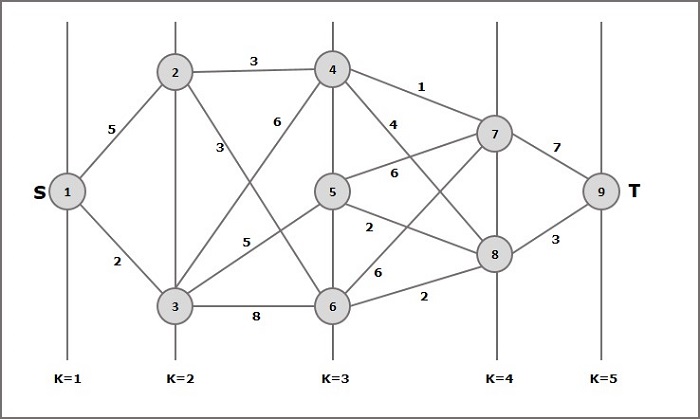
Menurut rumusnya, kita harus menghitung biayanya (i, j) menggunakan langkah-langkah berikut
Langkah-1: Biaya (K-2, j)
Pada langkah ini, tiga node (node 4, 5. 6) dipilih sebagai j. Karenanya, kami memiliki tiga opsi untuk memilih biaya minimum pada langkah ini.
Biaya (3, 4) = min {c (4, 7) + Biaya (7, 9), c (4, 8) + Biaya (8, 9)} = 7
Biaya (3, 5) = min {c (5, 7) + Biaya (7, 9), c (5, 8) + Biaya (8, 9)} = 5
Biaya (3, 6) = min {c (6, 7) + Biaya (7, 9), c (6, 8) + Biaya (8, 9)} = 5
Langkah-2: Biaya (K-3, j)
Dipilih dua node sebagai j karena pada tahap k - 3 = 2 terdapat dua node yaitu 2 dan 3. Jadi nilai i = 2 dan j = 2 dan 3.
Biaya (2, 2) = min {c (2, 4) + Biaya (4, 8) + Biaya (8, 9), c (2, 6) +
Biaya (6, 8) + Biaya (8, 9)} = 8
Biaya (2, 3) = {c (3, 4) + Biaya (4, 8) + Biaya (8, 9), c (3, 5) + Biaya (5, 8) + Biaya (8, 9), c (3, 6) + Biaya (6, 8) + Biaya (8, 9)} = 10
Langkah-3: Biaya (K-4, j)
Biaya (1, 1) = {c (1, 2) + Biaya (2, 6) + Biaya (6, 8) + Biaya (8, 9), c (1, 3) + Biaya (3, 5) + Biaya (5, 8) + Biaya (8, 9))} = 12
c (1, 3) + Biaya (3, 6) + Biaya (6, 8 + Biaya (8, 9))} = 13
Oleh karena itu, jalur yang memiliki biaya minimum adalah 1→ 3→ 5→ 8→ 9.