Kelas NP Hard dan NP-Complete
Masalah ada di NPC kelas jika di NP dan sebagai hardsebagai masalah di NP. Masalahnya adalahNP-hard jika semua masalah di NP adalah polynomial time yang dapat direduksi menjadi itu, meskipun mungkin tidak ada di NP itu sendiri.
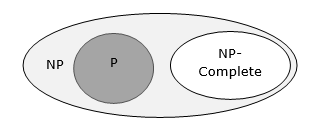
Jika algoritme waktu polinomial ada untuk salah satu masalah ini, semua masalah di NP akan dapat dipecahkan dengan waktu polinomial. Masalah ini disebutNP-complete. Fenomena kelengkapan NP penting baik untuk alasan teoretis maupun praktis.
Definisi NP-Kelengkapan
Sebuah bahasa B adalah NP-complete jika memenuhi dua kondisi
B ada di NP
Setiap A di NP adalah waktu polinomial yang dapat direduksi menjadi B.
Jika suatu bahasa memenuhi properti kedua, tetapi belum tentu yang pertama, bahasa B diketahui sebagai NP-Hard. Secara informal, masalah pencarianB adalah NP-Hard jika ada beberapa NP-Complete masalah A yang direduksi Turing menjadi B.
Masalah di NP-Hard tidak dapat diselesaikan dalam waktu polinomial, sampai P = NP. Jika suatu masalah terbukti sebagai NPC, tidak perlu membuang waktu untuk mencoba menemukan algoritma yang efisien untuk itu. Sebagai gantinya, kita dapat fokus pada algoritma pendekatan desain.
Masalah NP-Complete
Berikut adalah beberapa masalah NP-Complete, yang tidak diketahui algoritma waktu polinomialnya.
- Menentukan apakah graf memiliki siklus Hamiltonian
- Menentukan apakah rumus Boolean memuaskan, dll.
Masalah NP-Hard
Masalah berikut adalah NP-Hard
- Masalah kepuasan sirkuit
- Set Penutup
- Penutup Vertex
- Masalah Penjual Bepergian
Dalam konteks ini, sekarang kita akan membahas TSP yaitu NP-Complete
TSP adalah NP-Complete
Masalah salesman keliling terdiri dari seorang salesman dan sekumpulan kota. Penjual harus mengunjungi setiap kota mulai dari kota tertentu dan kembali ke kota yang sama. Tantangan dari masalah ini adalah penjual keliling ingin meminimalkan total lama perjalanan
Bukti
Untuk membuktikan TSP is NP-Complete, pertama kita harus membuktikannya TSP belongs to NP. Di TSP, kami menemukan tur dan memeriksa bahwa tur berisi setiap simpul satu kali. Kemudian total biaya tepi tur dihitung. Akhirnya, kami memeriksa apakah biayanya minimum. Ini dapat diselesaikan dalam waktu polinomial. JadiTSP belongs to NP.
Kedua, kita harus membuktikannya TSP is NP-hard. Untuk membuktikannya, salah satu caranya adalah dengan menunjukkannyaHamiltonian cycle ≤p TSP (seperti yang kita ketahui bahwa masalah siklus Hamiltonian adalah NPcomplete).
Menganggap G = (V, E) menjadi contoh siklus Hamiltonian.
Oleh karena itu, instance TSP dibangun. Kami membuat grafik lengkapG' = (V, E'), dimana
$$ E ^ {'} = \ lbrace (i, j) \ titik dua i, j \ in V \: \: dan \: i \ neq j $$
Jadi, fungsi biaya didefinisikan sebagai berikut -
$$ t (i, j) = \ begin {cases} 0 & if \: (i, j) \: \ in E \\ 1 & sebaliknya \ end {cases} $$
Sekarang, anggaplah itu siklus Hamiltonian h ada di G. Jelas bahwa biaya setiap sisi masukh adalah 0 di G' karena setiap sisi milik E. Karena itu,h memiliki biaya sebesar 0 di G'. Jadi, jika grafikG memiliki siklus Hamiltonian, lalu grafik G' memiliki tur 0 biaya.
Sebaliknya, kami berasumsi demikian G' mengadakan tur h' biaya paling banyak 0. Biaya tepi masukE' adalah 0 dan 1Menurut definisi. Oleh karena itu, setiap sisi harus memiliki biaya sebesar0 sebagai biaya h' adalah 0. Oleh karena itu kami menyimpulkan ituh' hanya berisi tepi dalam E.
Dengan demikian, kami telah membuktikannya G memiliki siklus Hamiltonian, jika dan hanya jika G' memiliki tur dengan biaya paling banyak 0. TSP adalah NP-complete.