DAA - Jalur Terpendek

Algoritma Dijkstra

Algoritma Dijkstra memecahkan masalah jalur terpendek sumber tunggal pada graf berbobot terarah G = (V, E) , di mana semua sisi non-negatif (yaitu, w (u, v) ≥ 0 untuk setiap sisi (u, v ) Є E ).

Dalam algoritma berikut, kita akan menggunakan satu fungsi Extract-Min(), yang mengekstrak node dengan kunci terkecil.

Algorithm: Dijkstra’s-Algorithm (G, w, s) 
for each vertex v Є G.V  
   v.d := ∞ 
   v.∏ := NIL 
s.d := 0 
S := Ф 
Q := G.V 
while Q ≠ Ф 
   u := Extract-Min (Q) 
   S := S U {u} 
   for each vertex v Є G.adj[u] 
      if v.d > u.d + w(u, v) 
         v.d := u.d + w(u, v) 
         v.∏ := u

Analisis

Kompleksitas algoritma ini sepenuhnya bergantung pada implementasi fungsi Extract-Min. Jika fungsi ekstrak min diimplementasikan menggunakan pencarian linier, kompleksitas algoritma ini adalahO(V² + E).

Dalam algoritma ini, jika kita menggunakan min-heap yang mana Extract-Min() berfungsi untuk mengembalikan node dari Q dengan kunci terkecil, kompleksitas algoritma ini dapat dikurangi lebih jauh.

Contoh

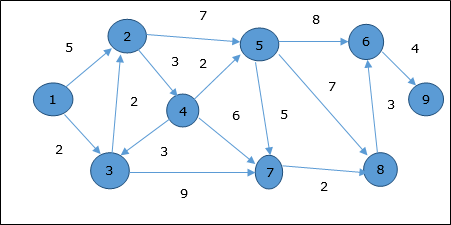
Mari kita pertimbangkan simpul 1 dan 9sebagai titik awal dan tujuan masing-masing. Awalnya, semua simpul kecuali simpul awal ditandai dengan ∞ dan simpul awal ditandai dengan0.

Puncak	Awal	Langkah1 V 1	Langkah2 V 3	Langkah3 V 2	Langkah4 V 4	Langkah5 V 5	Langkah6 V 7	Langkah7 V 8	Langkah8 V 6
1	0	0	0	0	0	0	0	0	0
2	∞	5	4	4	4	4	4	4	4
3	∞	2	2	2	2	2	2	2	2
4	∞	∞	∞	7	7	7	7	7	7
5	∞	∞	∞	11	9	9	9	9	9
6	∞	∞	∞	∞	∞	17	17	16	16
7	∞	∞	11	11	11	11	11	11	11
8	∞	∞	∞	∞	∞	16	13	13	13
9	∞	∞	∞	∞	∞	∞	∞	∞	20

Oleh karena itu, jarak minimum simpul 9 dari puncak 1 adalah 20. Dan jalannya adalah

1 → 3 → 7 → 8 → 6 → 9

Jalur ini ditentukan berdasarkan informasi pendahulu.

Algoritma Bellman Ford

Algoritme ini memecahkan masalah jalur terpendek sumber tunggal dari grafik berarah G = (V, E)di mana bobot tepinya mungkin negatif. Selain itu, algoritma ini dapat diterapkan untuk menemukan jalur terpendek, jika tidak ada siklus berbobot negatif.

Algorithm: Bellman-Ford-Algorithm (G, w, s) 
for each vertex v Є G.V  
   v.d := ∞ 
   v.∏ := NIL 
s.d := 0 
for i = 1 to |G.V| - 1 
   for each edge (u, v) Є G.E 
      if v.d > u.d + w(u, v) 
         v.d := u.d +w(u, v) 
         v.∏ := u 
for each edge (u, v) Є G.E 
   if v.d > u.d + w(u, v) 
      return FALSE 
return TRUE

Analisis

Pertama for loop digunakan untuk inisialisasi, yang berjalan di O(V)waktu. Selanjutnyafor putaran berjalan |V - 1| melewati tepi, yang mengambilO(E) waktu.

Karenanya, algoritme Bellman-Ford berjalan O(V, E) waktu.

Contoh

Contoh berikut menunjukkan cara kerja algoritma Bellman-Ford selangkah demi selangkah. Grafik ini memiliki sisi negatif tetapi tidak memiliki siklus negatif, maka masalahnya dapat diselesaikan dengan menggunakan teknik ini.

Pada saat inisialisasi, semua simpul kecuali sumber ditandai dengan ∞ dan sumber ditandai dengan 0.

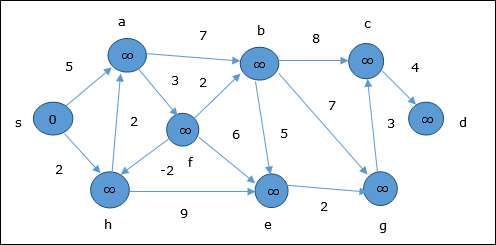
Pada langkah pertama, semua simpul yang dapat dijangkau dari sumber diperbarui dengan biaya minimum. Oleh karena itu, simpula dan h diperbarui.

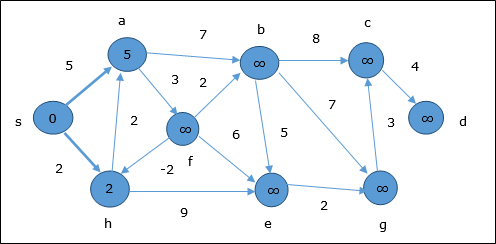
Pada langkah selanjutnya, simpul a, b, f dan e diperbarui.

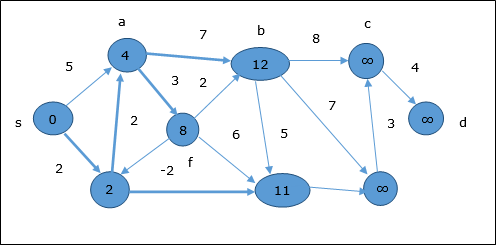
Mengikuti logika yang sama, di simpul langkah ini b, f, c dan g diperbarui.

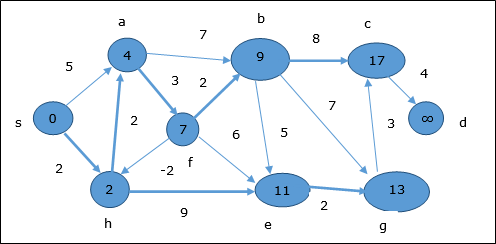
Di sini, simpul c dan d diperbarui.

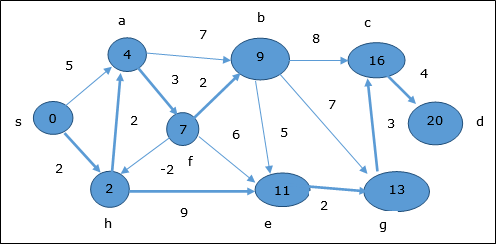
Oleh karena itu, jarak minimum antar simpul s dan simpul d adalah 20.

Berdasarkan informasi pendahulu, jalurnya adalah s → h → e → g → c → d