DAA - Panduan Cepat

Algoritme adalah sekumpulan langkah operasi untuk menyelesaikan masalah dalam melakukan kalkulasi, pemrosesan data, dan tugas penalaran otomatis. Algoritme adalah metode efisien yang dapat diekspresikan dalam waktu dan ruang yang terbatas.

Algoritme adalah cara terbaik untuk merepresentasikan solusi dari masalah tertentu dengan cara yang sangat sederhana dan efisien. Jika kita memiliki algoritme untuk masalah tertentu, maka kita dapat mengimplementasikannya dalam bahasa pemrograman apa pun, artinya filealgorithm is independent from any programming languages.

Desain Algoritma

Aspek penting dari perancangan algoritma antara lain membuat algoritma yang efisien untuk menyelesaikan suatu masalah secara efisien dengan menggunakan ruang dan waktu yang minimum.

Untuk memecahkan masalah, pendekatan yang berbeda dapat diikuti. Beberapa di antaranya dapat menjadi efisien sehubungan dengan konsumsi waktu, sedangkan pendekatan lain mungkin efisien dalam memori. Namun, perlu diingat bahwa konsumsi waktu dan penggunaan memori tidak dapat dioptimalkan secara bersamaan. Jika kita memerlukan algoritme untuk berjalan dalam waktu yang lebih singkat, kita harus menginvestasikan lebih banyak memori dan jika kita memerlukan algoritme untuk berjalan dengan memori yang lebih sedikit, kita perlu memiliki lebih banyak waktu.

Langkah Pengembangan Masalah

Langkah-langkah berikut terlibat dalam memecahkan masalah komputasi.

• Definisi masalah
• Pengembangan model
• Spesifikasi Algoritma
• Mendesain Algoritma
• Memeriksa kebenaran suatu Algoritma
• Analisis Algoritma
• Implementasi Algoritma
• Pengujian program
• Documentation

Karakteristik Algoritma

Karakteristik utama dari algoritma adalah sebagai berikut -

• Algoritme harus memiliki nama yang unik

• Algoritme harus memiliki kumpulan masukan dan keluaran yang didefinisikan secara eksplisit

• Algoritme tersusun dengan baik dengan operasi yang tidak ambigu

• Algoritme berhenti dalam waktu yang terbatas. Algoritme tidak boleh berjalan tanpa batas, artinya, algoritme harus diakhiri di beberapa titik

Pseudocode

Pseudocode memberikan deskripsi tingkat tinggi dari suatu algoritma tanpa ambiguitas yang terkait dengan teks biasa tetapi juga tanpa perlu mengetahui sintaks dari bahasa pemrograman tertentu.

Waktu berjalan dapat diperkirakan dengan cara yang lebih umum dengan menggunakan Pseudocode untuk merepresentasikan algoritme sebagai satu set operasi dasar yang kemudian dapat dihitung.

Perbedaan antara Algoritma dan Pseudocode

Algoritme adalah definisi formal dengan beberapa karakteristik khusus yang menggambarkan suatu proses, yang dapat dijalankan oleh mesin komputer Turing-complete untuk melakukan tugas tertentu. Secara umum, kata "algoritme" dapat digunakan untuk mendeskripsikan tugas tingkat tinggi apa pun dalam ilmu komputer.

Di sisi lain, pseudocode adalah deskripsi algoritme informal dan (seringkali belum sempurna) yang dapat dibaca manusia yang meninggalkan banyak detail granular darinya. Menulis pseudocode tidak memiliki batasan gaya dan satu-satunya tujuan adalah untuk mendeskripsikan langkah-langkah algoritme tingkat tinggi dengan cara yang lebih realistis dalam bahasa alami.

Sebagai contoh, berikut adalah algoritma untuk Insertion Sort.

Algorithm: Insertion-Sort 
Input: A list L of integers of length n  
Output: A sorted list L1 containing those integers present in L 
Step 1: Keep a sorted list L1 which starts off empty  
Step 2: Perform Step 3 for each element in the original list L  
Step 3: Insert it into the correct position in the sorted list L1.  
Step 4: Return the sorted list 
Step 5: Stop

Berikut ini adalah pseudocode yang menjelaskan bagaimana proses abstrak tingkat tinggi yang disebutkan di atas dalam algoritma Insertion-Sort dapat dijelaskan dengan cara yang lebih realistis.

for i <- 1 to length(A) 
   x <- A[i] 
   j <- i 
   while j > 0 and A[j-1] > x 
      A[j] <- A[j-1] 
      j <- j - 1 
   A[j] <- x

Dalam tutorial ini, algoritma akan disajikan dalam bentuk pseudocode, yang dalam banyak hal mirip dengan C, C ++, Java, Python, dan bahasa pemrograman lainnya.

Dalam analisis teoritis algoritme, adalah umum untuk memperkirakan kompleksitasnya dalam pengertian asimtotik, yaitu, untuk memperkirakan fungsi kompleksitas untuk input besar yang sewenang-wenang. Syarat"analysis of algorithms" diciptakan oleh Donald Knuth.

Analisis algoritme adalah bagian penting dari teori kompleksitas komputasi, yang memberikan estimasi teoretis untuk sumber daya yang diperlukan dari suatu algoritme untuk memecahkan masalah komputasi tertentu. Sebagian besar algoritme dirancang untuk bekerja dengan input dengan panjang sembarang. Analisis algoritma adalah penentuan jumlah waktu dan sumber daya ruang yang dibutuhkan untuk mengeksekusinya.

Biasanya, efisiensi atau waktu berjalan suatu algoritma dinyatakan sebagai fungsi yang menghubungkan panjang input dengan jumlah langkah yang disebut time complexity, atau volume memori, yang dikenal sebagai space complexity.

Kebutuhan Analisis

Pada bab ini, kita akan membahas perlunya analisis algoritma dan bagaimana memilih algoritma yang lebih baik untuk masalah tertentu karena satu masalah komputasi dapat diselesaikan dengan algoritma yang berbeda.

Dengan mempertimbangkan suatu algoritma untuk suatu masalah tertentu, kita dapat mulai mengembangkan pengenalan pola sehingga jenis masalah yang serupa dapat diselesaikan dengan bantuan algoritma ini.

Algoritme seringkali sangat berbeda satu sama lain, meskipun tujuan dari algoritme ini sama. Misalnya, kita tahu bahwa sekumpulan angka dapat diurutkan menggunakan algoritme yang berbeda. Jumlah perbandingan yang dilakukan oleh satu algoritme mungkin berbeda dengan algoritme lain untuk input yang sama. Karenanya, kompleksitas waktu dari algoritme tersebut mungkin berbeda. Pada saat yang sama, kita perlu menghitung ruang memori yang dibutuhkan oleh setiap algoritma.

Analisis algoritma adalah proses menganalisis kemampuan pemecahan masalah dari algoritma dalam hal waktu dan ukuran yang dibutuhkan (ukuran memori untuk penyimpanan selama implementasi). Namun, perhatian utama dari analisis algoritma adalah waktu atau kinerja yang dibutuhkan. Umumnya, kami melakukan jenis analisis berikut -

• Worst-case - Jumlah langkah maksimum yang diambil pada setiap contoh ukuran a.

• Best-case - Jumlah langkah minimum yang diambil pada setiap contoh ukuran a.

• Average case - Jumlah rata-rata langkah yang diambil pada setiap contoh ukuran a.

• Amortized - Urutan operasi yang diterapkan ke input ukuran a dirata-rata dari waktu ke waktu.

Untuk memecahkan masalah, kita perlu mempertimbangkan waktu serta kompleksitas ruang karena program dapat berjalan pada sistem di mana memori terbatas tetapi tersedia ruang yang memadai atau mungkin sebaliknya. Dalam konteks ini, jika kita membandingkanbubble sort dan merge sort. Jenis gelembung tidak memerlukan memori tambahan, tetapi jenis penggabungan memerlukan ruang tambahan. Meskipun kompleksitas waktu jenis gelembung lebih tinggi dibandingkan dengan jenis gabungan, kita mungkin perlu menerapkan jenis gelembung jika program perlu dijalankan di lingkungan, di mana memori sangat terbatas.

Untuk mengukur konsumsi sumber daya suatu algoritma, berbagai strategi digunakan seperti yang dibahas dalam bab ini.

Analisis Asymptotic

Perilaku asimtotik suatu fungsi f(n) mengacu pada pertumbuhan f(n) sebagai n menjadi besar.

Kami biasanya mengabaikan nilai kecil n, karena kami biasanya tertarik untuk memperkirakan seberapa lambat program akan mendapatkan input yang besar.

Aturan praktis yang baik adalah semakin lambat laju pertumbuhan asimtotik, semakin baik algoritme. Padahal itu tidak selalu benar.

Misalnya, algoritme linier $f(n) = d * n + k$ selalu lebih baik secara asimtotik daripada kuadratik, $f(n) = c.n^2 + q$.

Memecahkan Persamaan Pengulangan

Pengulangan adalah persamaan atau pertidaksamaan yang mendeskripsikan fungsi dalam hal nilainya pada input yang lebih kecil. Pengulangan umumnya digunakan dalam paradigma divide-and-conquer.

Mari kita pertimbangkan T(n) menjadi waktu berjalan pada masalah ukuran n.

Jika ukuran masalahnya cukup kecil, katakan n < c dimana c adalah konstanta, solusi langsung membutuhkan waktu konstan, yang ditulis sebagai θ(1). Jika pembagian masalah menghasilkan sejumlah sub-masalah dengan ukuran$\frac{n}{b}$.

Untuk mengatasi masalah tersebut, waktu yang dibutuhkan adalah a.T(n/b). Jika kita perhatikan waktu yang dibutuhkan untuk pembagian tersebutD(n) dan waktu yang dibutuhkan untuk menggabungkan hasil sub-masalah adalah C(n), relasi perulangan dapat direpresentasikan sebagai -

$$T(n)=\begin{cases}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\theta(1) & if\:n\leqslant c\\a T(\frac{n}{b})+D(n)+C(n) & otherwise\end{cases}$$

Relasi pengulangan dapat diselesaikan menggunakan metode berikut -

• Substitution Method - Dalam metode ini, kami menebak batasan dan menggunakan induksi matematika kami membuktikan bahwa asumsi kami benar.

• Recursion Tree Method - Dalam metode ini, pohon pengulangan dibentuk di mana setiap node mewakili biaya.

• Master’s Theorem - Ini adalah teknik penting lainnya untuk menemukan kompleksitas relasi pengulangan.

Analisis Amortisasi

Analisis diamortisasi umumnya digunakan untuk algoritme tertentu di mana urutan operasi serupa dilakukan.

• Analisis diamortisasi memberikan batasan pada biaya sebenarnya dari seluruh urutan, daripada membatasi biaya urutan operasi secara terpisah.

• Analisis diamortisasi berbeda dari analisis kasus rata-rata; probabilitas tidak terlibat dalam analisis diamortisasi. Analisis diamortisasi menjamin kinerja rata-rata setiap operasi dalam kasus terburuk.

Ini bukan hanya alat untuk analisis, ini adalah cara berpikir tentang desain, karena desain dan analisis sangat erat kaitannya.

Metode Agregat

Metode agregat memberikan pandangan global tentang suatu masalah. Dalam metode ini, jikan operasi membutuhkan waktu kasus terburuk T(n)secara keseluruhan. Kemudian biaya perolehan diamortisasi dari setiap operasi adalahT(n)/n. Meskipun operasi yang berbeda mungkin memerlukan waktu yang berbeda, dalam metode ini biaya yang bervariasi diabaikan.

Metode Akuntansi

Dalam metode ini, biaya yang berbeda diberikan untuk operasi yang berbeda sesuai dengan biaya sebenarnya. Jika biaya perolehan diamortisasi dari suatu operasi melebihi biaya sebenarnya, selisihnya ditetapkan ke objek sebagai kredit. Kredit ini membantu untuk membayar operasi selanjutnya dimana biaya perolehan diamortisasi kurang dari biaya sebenarnya.

Jika biaya aktual dan biaya perolehan diamortisasi i^th operasi $c_{i}$ dan $\hat{c_{l}}$, kemudian

$$\displaystyle\sum\limits_{i=1}^n \hat{c_{l}}\geqslant\displaystyle\sum\limits_{i=1}^n c_{i}$$

Metode Potensial

Metode ini merepresentasikan pekerjaan prabayar sebagai energi potensial, daripada menganggap pekerjaan prabayar sebagai kredit. Energi ini dapat dilepaskan untuk membiayai operasi di masa depan.

Jika kami tampil n operasi yang dimulai dengan struktur data awal D₀. Mari kita pertimbangkan,c_i sebagai biaya aktual dan D_i sebagai struktur data i^thoperasi. Fungsi potensial Ф memetakan ke bilangan real Ф (D_i), potensi terkait dari D_i. Biaya perolehan diamortisasi$\hat{c_{l}}$ dapat didefinisikan dengan

$$\hat{c_{l}}=c_{i}+\Phi (D_{i})-\Phi (D_{i-1})$$

Jadi, total biaya perolehan diamortisasi adalah

$$\displaystyle\sum\limits_{i=1}^n \hat{c_{l}}=\displaystyle\sum\limits_{i=1}^n (c_{i}+\Phi (D_{i})-\Phi (D_{i-1}))=\displaystyle\sum\limits_{i=1}^n c_{i}+\Phi (D_{n})-\Phi (D_{0})$$

Tabel Dinamis

Jika ruang yang dialokasikan untuk tabel tidak cukup, kita harus menyalin tabel ke tabel ukuran yang lebih besar. Demikian pula, jika sejumlah besar anggota terhapus dari tabel, sebaiknya alokasikan kembali tabel dengan ukuran yang lebih kecil.

Dengan menggunakan analisis diamortisasi, kita dapat menunjukkan bahwa biaya penyisipan dan penghapusan diamortisasi adalah konstan dan ruang yang tidak terpakai dalam tabel dinamis tidak pernah melebihi pecahan konstan dari total ruang.

Pada bab selanjutnya dari tutorial ini, kita akan membahas Notasi Asymptotic secara singkat.

Dalam perancangan Algoritma, analisis kompleksitas suatu algoritma merupakan aspek yang esensial. Terutama, kompleksitas algoritmik berkaitan dengan kinerjanya, seberapa cepat atau lambat kerjanya.

Kompleksitas suatu algoritma menggambarkan efisiensi algoritma dalam hal jumlah memori yang dibutuhkan untuk memproses data dan waktu pemrosesan.

Kompleksitas algoritma dianalisis dalam dua perspektif: Time dan Space.

Kompleksitas Waktu

Ini adalah fungsi yang menjelaskan jumlah waktu yang diperlukan untuk menjalankan algoritme dalam hal ukuran input. "Waktu" dapat berarti jumlah akses memori yang dilakukan, jumlah perbandingan antara bilangan bulat, berapa kali beberapa loop dalam dijalankan, atau beberapa unit alami lainnya yang terkait dengan jumlah waktu nyata yang dibutuhkan algoritme.

Kompleksitas Ruang

Ini adalah fungsi yang mendeskripsikan jumlah memori yang diambil algoritme dalam hal ukuran input ke algoritme. Kita sering berbicara tentang memori "ekstra" yang dibutuhkan, tidak termasuk memori yang dibutuhkan untuk menyimpan input itu sendiri. Sekali lagi, kami menggunakan satuan alami (tapi panjang tetap) untuk mengukurnya.

Kompleksitas ruang terkadang diabaikan karena ruang yang digunakan minimal dan / atau jelas, namun terkadang menjadi masalah yang sama pentingnya dengan waktu.

Notasi Asymptotic

Waktu eksekusi suatu algoritme bergantung pada set instruksi, kecepatan prosesor, kecepatan I / O disk, dll. Oleh karena itu, kami memperkirakan efisiensi algoritme secara asimtotik.

Fungsi waktu dari suatu algoritma diwakili oleh T(n), dimana n adalah ukuran masukan.

Berbagai jenis notasi asimtotik digunakan untuk merepresentasikan kompleksitas algoritme. Notasi asimtotik berikut digunakan untuk menghitung kompleksitas waktu berjalan dari suatu algoritma.

• O - Big Oh

• Ω - Omega besar

• θ - Theta besar

• o - Little Oh

• ω - Sedikit omega

O: Batas Atas Asymptotic

'O' (Big Oh) adalah notasi yang paling umum digunakan. Sebuah fungsif(n) dapat diwakili adalah urutan g(n) itu adalah O(g(n)), jika ada nilai bilangan bulat positif n sebagai n₀ dan konstanta positif c sedemikian rupa sehingga -

$f(n)\leqslant c.g(n)$ untuk $n > n_{0}$ dalam semua kasus

Karenanya, fungsi g(n) adalah batas atas untuk fungsi f(n), sebagai g(n) tumbuh lebih cepat dari f(n).

Contoh

Mari kita pertimbangkan fungsi yang diberikan, $f(n) = 4.n^3 + 10.n^2 + 5.n + 1$

Mengingat $g(n) = n^3$,

$f(n)\leqslant 5.g(n)$ untuk semua nilai $n > 2$

Oleh karena itu, kompleksitas f(n) dapat direpresentasikan sebagai $O(g(n))$, yaitu $O(n^3)$

Ω: Batas Bawah Asymptotic

Kami mengatakan itu $f(n) = \Omega (g(n))$ ketika ada konstanta c bahwa $f(n)\geqslant c.g(n)$ untuk semua nilai yang cukup besar n. Sininadalah bilangan bulat positif. Artinya fungsig adalah batas bawah untuk fungsi f; setelah nilai tertentun, f tidak akan pernah pergi ke bawah g.

Contoh

Mari kita pertimbangkan fungsi yang diberikan, $f(n) = 4.n^3 + 10.n^2 + 5.n + 1$.

Mengingat $g(n) = n^3$, $f(n)\geqslant 4.g(n)$ untuk semua nilai $n > 0$.

Oleh karena itu, kompleksitas f(n) dapat direpresentasikan sebagai $\Omega (g(n))$, yaitu $\Omega (n^3)$

θ: Asymptotic Tight Bound

Kami mengatakan itu $f(n) = \theta(g(n))$ ketika ada konstanta c₁ dan c₂ bahwa $c_{1}.g(n) \leqslant f(n) \leqslant c_{2}.g(n)$ untuk semua nilai yang cukup besar n. Sinin adalah bilangan bulat positif.

Artinya fungsi g adalah batasan yang ketat untuk fungsi f.

Contoh

Mari kita pertimbangkan fungsi yang diberikan, $f(n) = 4.n^3 + 10.n^2 + 5.n + 1$

Mengingat $g(n) = n^3$, $4.g(n) \leqslant f(n) \leqslant 5.g(n)$ untuk semua nilai besar n.

Oleh karena itu, kompleksitas f(n) dapat direpresentasikan sebagai $\theta (g(n))$, yaitu $\theta (n^3)$.

O - Notasi

Batas atas asimtotik yang disediakan oleh O-notationmungkin ketat atau mungkin tidak asimtotik. Terikat$2.n^2 = O(n^2)$ ketat secara asimtotik, tetapi terikat $2.n = O(n^2)$ tidak.

Kita gunakan o-notation untuk menunjukkan batas atas yang tidak kencang secara asimtotik.

Kami mendefinisikan secara resmi o(g(n)) (little-oh of g of n) sebagai himpunan f(n) = o(g(n)) untuk setiap konstanta positif $c > 0$ dan ada nilai $n_{0} > 0$, seperti yang $0 \leqslant f(n) \leqslant c.g(n)$.

Secara intuitif, di o-notation, fungsinya f(n) menjadi relatif tidak signifikan terhadap g(n) sebagai nmendekati tak terbatas; itu adalah,

$$\lim_{n \rightarrow \infty}\left(\frac{f(n)}{g(n)}\right) = 0$$

Contoh

Mari kita perhatikan fungsi yang sama, $f(n) = 4.n^3 + 10.n^2 + 5.n + 1$

Mengingat $g(n) = n^{4}$,

$$\lim_{n \rightarrow \infty}\left(\frac{4.n^3 + 10.n^2 + 5.n + 1}{n^4}\right) = 0$$

Oleh karena itu, kompleksitas f(n) dapat direpresentasikan sebagai $o(g(n))$, yaitu $o(n^4)$.

ω - Notasi

Kita gunakan ω-notationuntuk menunjukkan batas bawah yang tidak kencang secara asimtotik. Namun secara formal, kami mendefinisikanω(g(n)) (sedikit omega dari g dari n) sebagai himpunan f(n) = ω(g(n)) untuk setiap konstanta positif C > 0 dan ada nilai $n_{0} > 0$, sehingga $ 0 \ leqslant cg (n) <f (n) $.

Sebagai contoh, $\frac{n^2}{2} = \omega (n)$, tapi $\frac{n^2}{2} \neq \omega (n^2)$. Relasi$f(n) = \omega (g(n))$ menyiratkan bahwa ada batas berikut

$$\lim_{n \rightarrow \infty}\left(\frac{f(n)}{g(n)}\right) = \infty$$

Itu adalah, f(n) menjadi relatif besar secara sewenang-wenang g(n) sebagai n mendekati tak terbatas.

Contoh

Mari kita pertimbangkan fungsi yang sama, $f(n) = 4.n^3 + 10.n^2 + 5.n + 1$

Mengingat $g(n) = n^2$,

$$\lim_{n \rightarrow \infty}\left(\frac{4.n^3 + 10.n^2 + 5.n + 1}{n^2}\right) = \infty$$

Oleh karena itu, kompleksitas f(n) dapat direpresentasikan sebagai $o(g(n))$, yaitu $\omega (n^2)$.

Analisis Apriori dan Apostiari

Analisis apriori artinya, analisis dilakukan sebelum dijalankan pada sistem tertentu. Analisis ini merupakan tahapan dimana suatu fungsi didefinisikan menggunakan beberapa model teoritis. Oleh karena itu, kami menentukan kompleksitas waktu dan ruang dari suatu algoritme dengan hanya melihat algoritme tersebut daripada menjalankannya pada sistem tertentu dengan memori, prosesor, dan kompiler yang berbeda.

Analisis apostiari suatu algoritma berarti kita melakukan analisis suatu algoritma hanya setelah menjalankannya pada suatu sistem. Ini secara langsung tergantung pada sistem dan perubahan dari sistem ke sistem.

Dalam suatu industri, kami tidak dapat melakukan analisis Apostiari karena perangkat lunak umumnya dibuat untuk pengguna anonim, yang menjalankannya pada sistem yang berbeda dari yang ada di industri.

Di Apriori, itulah alasan kami menggunakan notasi asimtotik untuk menentukan kompleksitas ruang dan waktu saat mereka berubah dari komputer ke komputer; namun, secara asimtotik keduanya sama.

Dalam bab ini, kita akan membahas kompleksitas masalah komputasi sehubungan dengan jumlah ruang yang dibutuhkan algoritme.

Kompleksitas ruang berbagi banyak fitur kompleksitas waktu dan berfungsi sebagai cara lebih lanjut untuk mengklasifikasikan masalah menurut kesulitan komputasi mereka.

Apa itu Space Complexity?

Kompleksitas ruang adalah fungsi yang menjelaskan jumlah memori (ruang) yang diambil algoritme dalam hal jumlah input ke algoritme.

Kita sering membicarakannya extra memorydibutuhkan, tidak termasuk memori yang dibutuhkan untuk menyimpan input itu sendiri. Sekali lagi, kami menggunakan satuan alami (tapi panjang tetap) untuk mengukurnya.

Kita dapat menggunakan byte, tetapi lebih mudah digunakan, katakanlah, jumlah bilangan bulat yang digunakan, jumlah struktur berukuran tetap, dll.

Pada akhirnya, fungsi yang kita hasilkan tidak bergantung pada jumlah byte sebenarnya yang diperlukan untuk mewakili unit.

Kompleksitas ruang terkadang diabaikan karena ruang yang digunakan minimal dan / atau jelas, namun terkadang menjadi masalah yang sama pentingnya dengan kompleksitas waktu

Definisi

Membiarkan M menjadi deterministik Turing machine (TM)yang menghentikan semua input. Kompleksitas ruangM adalah fungsinya $f \colon N \rightarrow N$, dimana f(n) adalah jumlah maksimum sel tape dan M memindai input dengan panjang apa pun M. Jika kompleksitas ruangM adalah f(n), kita bisa bilang begitu M berjalan di luar angkasa f(n).

Kami memperkirakan kompleksitas ruang mesin Turing dengan menggunakan notasi asimtotik.

Membiarkan $f \colon N \rightarrow R^+$menjadi sebuah fungsi. Kelas kompleksitas ruang dapat didefinisikan sebagai berikut -

SPACE = {L | L is a language decided by an O(f(n)) space deterministic TM}

SPACE = {L | L is a language decided by an O(f(n)) space non-deterministic TM}

PSPACE adalah kelas bahasa yang dapat didekripsi dalam ruang polinomial pada mesin Turing deterministik.

Dengan kata lain, PSPACE = U_k SPACE (n^k)

Teorema Savitch

Salah satu teorema paling awal yang terkait dengan kompleksitas ruang adalah teorema Savitch. Menurut teorema ini, mesin deterministik dapat mensimulasikan mesin non-deterministik dengan menggunakan sedikit ruang.

Untuk kompleksitas waktu, simulasi semacam itu tampaknya membutuhkan peningkatan waktu secara eksponensial. Untuk kompleksitas ruang, teorema ini menunjukkan bahwa setiap mesin Turing non deterministik yang digunakanf(n) ruang dapat diubah menjadi TM deterministik yang digunakan f²(n) ruang.

Oleh karena itu, teorema Savitch menyatakan bahwa, untuk fungsi apa pun, $f \colon N \rightarrow R^+$, dimana $f(n) \geqslant n$

NSPACE(f(n)) ⊆ SPACE(f(n))

Hubungan Antar Kelas Kompleksitas

Diagram berikut menggambarkan hubungan antara kelas kompleksitas yang berbeda.

Sampai sekarang, kami belum membahas kelas P dan NP dalam tutorial ini. Ini akan dibahas nanti.

Banyak algoritme bersifat rekursif untuk menyelesaikan masalah tertentu secara rekursif menangani sub-masalah.

Di divide and conquer approach, sebuah masalah dibagi menjadi beberapa masalah yang lebih kecil, kemudian masalah yang lebih kecil diselesaikan secara mandiri, dan akhirnya solusi dari masalah yang lebih kecil digabungkan menjadi solusi untuk masalah besar.

Umumnya, algoritme bagi-dan-taklukkan memiliki tiga bagian -

• Divide the problem menjadi sejumlah sub-masalah yang merupakan contoh kecil dari masalah yang sama.

• Conquer the sub-problemsdengan memecahkannya secara rekursif. Jika cukup kecil, selesaikan sub-masalah sebagai kasus dasar.

• Combine the solutions ke sub masalah menjadi solusi untuk masalah aslinya.

Pro dan kontra dari Divide and Conquer Approach

Pendekatan divide and conquer mendukung paralelisme karena sub-masalah bersifat independen. Oleh karena itu, algoritma yang dirancang dengan menggunakan teknik ini, dapat berjalan pada sistem multiprosesor atau pada mesin yang berbeda secara bersamaan.

Dalam pendekatan ini, sebagian besar algoritma dirancang dengan menggunakan rekursi, oleh karena itu manajemen memori sangat tinggi. Untuk stack fungsi rekursif digunakan, di mana status fungsi perlu disimpan.

Penerapan Pendekatan Divide and Conquer

Berikut beberapa permasalahan yang diselesaikan dengan pendekatan divide and conquer.

• Menemukan maksimum dan minimum deret angka
• Perkalian matriks Strassen
• Gabungkan urutan
• Pencarian biner

Mari kita bahas satu masalah sederhana yang bisa diselesaikan dengan teknik divide and conquer.

Pernyataan masalah

Masalah Max-Min dalam analisis algoritma adalah menemukan nilai maksimum dan minimum dalam sebuah array.

Larutan

Untuk menemukan angka maksimum dan minimum dalam larik tertentu numbers[] ukuran n, algoritme berikut dapat digunakan. Pertama kami mewakilinaive method dan kemudian kami akan mempresentasikan divide and conquer approach.

Metode Naif

Metode naif adalah metode dasar untuk menyelesaikan masalah apa pun. Dalam metode ini, jumlah maksimum dan minimum dapat ditemukan secara terpisah. Untuk mencari angka maksimum dan minimum, algoritma langsung berikut dapat digunakan.

Algorithm: Max-Min-Element (numbers[]) 
max := numbers[1] 
min := numbers[1] 

for i = 2 to n do 
   if numbers[i] > max then  
      max := numbers[i] 
   if numbers[i] < min then  
      min := numbers[i] 
return (max, min)

Analisis

Jumlah perbandingan dalam metode Naive adalah 2n - 2.

Jumlah perbandingan dapat dikurangi dengan menggunakan pendekatan divide and conquer. Berikut tekniknya.

Bagi dan Taklukkan Pendekatan

Dalam pendekatan ini, larik dibagi menjadi dua bagian. Kemudian menggunakan pendekatan rekursif, jumlah maksimum dan minimum di setiap bagian ditemukan. Nanti, kembalikan maksimum dua maksimum dari setiap setengah dan minimum dua minimum dari setiap setengah.

Dalam soal yang diberikan ini, jumlah elemen dalam sebuah array adalah $y - x + 1$, dimana y lebih besar atau sama dengan x.

$\mathbf{\mathit{Max - Min(x, y)}}$ akan mengembalikan nilai maksimum dan minimum dari sebuah array $\mathbf{\mathit{numbers[x...y]}}$.

Algorithm: Max - Min(x, y) 
if y – x ≤ 1 then  
   return (max(numbers[x], numbers[y]), min((numbers[x], numbers[y])) 
else 
   (max1, min1):= maxmin(x, ⌊((x + y)/2)⌋) 
   (max2, min2):= maxmin(⌊((x + y)/2) + 1)⌋,y) 
return (max(max1, max2), min(min1, min2))

Analisis

Let T(n) be the number of comparisons made by $\mathbf{\mathit{Max - Min(x, y)}}$, where the number of elements $n = y - x + 1$.

If T(n) represents the numbers, then the recurrence relation can be represented as

$$T(n) = \begin{cases}T\left(\lfloor\frac{n}{2}\rfloor\right)+T\left(\lceil\frac{n}{2}\rceil\right)+2 & for\: n>2\\1 & for\:n = 2 \\0 & for\:n = 1\end{cases}$$

Let us assume that n is in the form of power of 2. Hence, n = 2^k where k is height of the recursion tree.

So,

$$T(n) = 2.T (\frac{n}{2}) + 2 = 2.\left(\begin{array}{c}2.T(\frac{n}{4}) + 2\end{array}\right) + 2 ..... = \frac{3n}{2} - 2$$

Compared to Naïve method, in divide and conquer approach, the number of comparisons is less. However, using the asymptotic notation both of the approaches are represented by O(n).

In this chapter, we will discuss merge sort and analyze its complexity.

Problem Statement

The problem of sorting a list of numbers lends itself immediately to a divide-and-conquer strategy: split the list into two halves, recursively sort each half, and then merge the two sorted sub-lists.

Solution

In this algorithm, the numbers are stored in an array numbers[]. Here, p and q represents the start and end index of a sub-array.

Algorithm: Merge-Sort (numbers[], p, r) 
if p < r then  
q = ⌊(p + r) / 2⌋ 
Merge-Sort (numbers[], p, q) 
    Merge-Sort (numbers[], q + 1, r) 
    Merge (numbers[], p, q, r)

Function: Merge (numbers[], p, q, r)
n1 = q – p + 1 
n2 = r – q 
declare leftnums[1…n1 + 1] and rightnums[1…n2 + 1] temporary arrays 
for i = 1 to n1 
   leftnums[i] = numbers[p + i - 1] 
for j = 1 to n2 
   rightnums[j] = numbers[q+ j] 
leftnums[n1 + 1] = ∞ 
rightnums[n2 + 1] = ∞ 
i = 1 
j = 1 
for k = p to r 
   if leftnums[i] ≤ rightnums[j] 
      numbers[k] = leftnums[i] 
      i = i + 1 
   else
      numbers[k] = rightnums[j] 
      j = j + 1

Analysis

Let us consider, the running time of Merge-Sort as T(n). Hence,

$T(n)=\begin{cases}c & if\:n\leqslant 1\\2\:x\:T(\frac{n}{2})+d\:x\:n & otherwise\end{cases}$ where c and d are constants

Therefore, using this recurrence relation,

$$T(n) = 2^i T(\frac{n}{2^i}) + i.d.n$$

As, $i = log\:n,\: T(n) = 2^{log\:n} T(\frac{n}{2^{log\:n}}) + log\:n.d.n$

$=\:c.n + d.n.log\:n$

Therefore, $T(n) = O(n\:log\:n)$

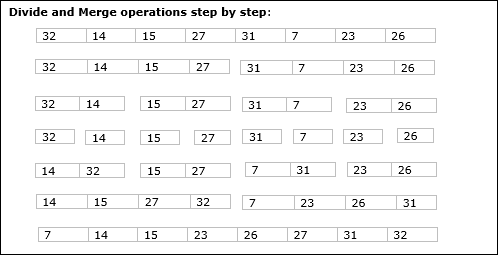
Example

In the following example, we have shown Merge-Sort algorithm step by step. First, every iteration array is divided into two sub-arrays, until the sub-array contains only one element. When these sub-arrays cannot be divided further, then merge operations are performed.

In this chapter, we will discuss another algorithm based on divide and conquer method.

Problem Statement

Binary search can be performed on a sorted array. In this approach, the index of an element x is determined if the element belongs to the list of elements. If the array is unsorted, linear search is used to determine the position.

Solution

In this algorithm, we want to find whether element x belongs to a set of numbers stored in an array numbers[]. Where l and r represent the left and right index of a sub-array in which searching operation should be performed.

Algorithm: Binary-Search(numbers[], x, l, r)
if l = r then  
   return l  
else 
   m := ⌊(l + r) / 2⌋ 
   if x ≤ numbers[m]  then 
      return Binary-Search(numbers[], x, l, m) 
   else 
      return Binary-Search(numbers[], x, m+1, r)

Analysis

Linear search runs in O(n) time. Whereas binary search produces the result in O(log n) time

Let T(n) be the number of comparisons in worst-case in an array of n elements.

Hence,

$$T(n)=\begin{cases}0 & if\:n= 1\\T(\frac{n}{2})+1 & otherwise\end{cases}$$

Using this recurrence relation $T(n) = log\:n$.

Therefore, binary search uses $O(log\:n)$ time.

Example

In this example, we are going to search element 63.

In this chapter, first we will discuss the general method of matrix multiplication and later we will discuss Strassen’s matrix multiplication algorithm.

Problem Statement

Let us consider two matrices X and Y. We want to calculate the resultant matrix Z by multiplying X and Y.

Naïve Method

First, we will discuss naïve method and its complexity. Here, we are calculating Z = X × Y. Using Naïve method, two matrices (X and Y) can be multiplied if the order of these matrices are p × q and q × r. Following is the algorithm.

Algorithm: Matrix-Multiplication (X, Y, Z) 
for i = 1 to p do 
   for j = 1 to r do 
      Z[i,j] := 0 
      for k = 1 to q do 
         Z[i,j] := Z[i,j] + X[i,k] × Y[k,j]

Complexity

Here, we assume that integer operations take O(1) time. There are three for loops in this algorithm and one is nested in other. Hence, the algorithm takes O(n³) time to execute.

Strassen’s Matrix Multiplication Algorithm

In this context, using Strassen’s Matrix multiplication algorithm, the time consumption can be improved a little bit.

Strassen’s Matrix multiplication can be performed only on square matrices where n is a power of 2. Order of both of the matrices are n × n.

Divide X, Y and Z into four (n/2)×(n/2) matrices as represented below −

$Z = \begin{bmatrix}I & J \\K & L \end{bmatrix}$ $X = \begin{bmatrix}A & B \\C & D \end{bmatrix}$ and $Y = \begin{bmatrix}E & F \\G & H \end{bmatrix}$

Using Strassen’s Algorithm compute the following −

$$M_{1} \: \colon= (A+C) \times (E+F)$$

$$M_{2} \: \colon= (B+D) \times (G+H)$$

$$M_{3} \: \colon= (A-D) \times (E+H)$$

$$M_{4} \: \colon= A \times (F-H)$$

$$M_{5} \: \colon= (C+D) \times (E)$$

$$M_{6} \: \colon= (A+B) \times (H)$$

$$M_{7} \: \colon= D \times (G-E)$$

Then,

$$I \: \colon= M_{2} + M_{3} - M_{6} - M_{7}$$

$$J \: \colon= M_{4} + M_{6}$$

$$K \: \colon= M_{5} + M_{7}$$

$$L \: \colon= M_{1} - M_{3} - M_{4} - M_{5}$$

Analysis

$T(n)=\begin{cases}c & if\:n= 1\\7\:x\:T(\frac{n}{2})+d\:x\:n^2 & otherwise\end{cases}$ where c and d are constants

Using this recurrence relation, we get $T(n) = O(n^{log7})$

Hence, the complexity of Strassen’s matrix multiplication algorithm is $O(n^{log7})$.

Among all the algorithmic approaches, the simplest and straightforward approach is the Greedy method. In this approach, the decision is taken on the basis of current available information without worrying about the effect of the current decision in future.

Greedy algorithms build a solution part by part, choosing the next part in such a way, that it gives an immediate benefit. This approach never reconsiders the choices taken previously. This approach is mainly used to solve optimization problems. Greedy method is easy to implement and quite efficient in most of the cases. Hence, we can say that Greedy algorithm is an algorithmic paradigm based on heuristic that follows local optimal choice at each step with the hope of finding global optimal solution.

In many problems, it does not produce an optimal solution though it gives an approximate (near optimal) solution in a reasonable time.

Components of Greedy Algorithm

Greedy algorithms have the following five components −

• A candidate set − A solution is created from this set.

• A selection function − Used to choose the best candidate to be added to the solution.

• A feasibility function − Used to determine whether a candidate can be used to contribute to the solution.

• An objective function − Used to assign a value to a solution or a partial solution.

• A solution function − Used to indicate whether a complete solution has been reached.

Areas of Application

Greedy approach is used to solve many problems, such as

• Finding the shortest path between two vertices using Dijkstra’s algorithm.

• Finding the minimal spanning tree in a graph using Prim’s /Kruskal’s algorithm, etc.

Where Greedy Approach Fails

In many problems, Greedy algorithm fails to find an optimal solution, moreover it may produce a worst solution. Problems like Travelling Salesman and Knapsack cannot be solved using this approach.

The Greedy algorithm could be understood very well with a well-known problem referred to as Knapsack problem. Although the same problem could be solved by employing other algorithmic approaches, Greedy approach solves Fractional Knapsack problem reasonably in a good time. Let us discuss the Knapsack problem in detail.

Knapsack Problem

Given a set of items, each with a weight and a value, determine a subset of items to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible.

The knapsack problem is in combinatorial optimization problem. It appears as a subproblem in many, more complex mathematical models of real-world problems. One general approach to difficult problems is to identify the most restrictive constraint, ignore the others, solve a knapsack problem, and somehow adjust the solution to satisfy the ignored constraints.

Applications

In many cases of resource allocation along with some constraint, the problem can be derived in a similar way of Knapsack problem. Following is a set of example.

• Finding the least wasteful way to cut raw materials
• portfolio optimization
• Cutting stock problems

Problem Scenario

A thief is robbing a store and can carry a maximal weight of W into his knapsack. There are n items available in the store and weight of i^th item is w_i and its profit is p_i. What items should the thief take?

In this context, the items should be selected in such a way that the thief will carry those items for which he will gain maximum profit. Hence, the objective of the thief is to maximize the profit.

Based on the nature of the items, Knapsack problems are categorized as

• Fractional Knapsack
• Knapsack

Fractional Knapsack

In this case, items can be broken into smaller pieces, hence the thief can select fractions of items.

According to the problem statement,

• There are n items in the store

• Weight of i^th item $w_{i} > 0$

• Profit for i^th item $p_{i} > 0$ and

• Capacity of the Knapsack is W

In this version of Knapsack problem, items can be broken into smaller pieces. So, the thief may take only a fraction x_i of i^th item.

$$0 \leqslant x_{i} \leqslant 1$$

The i^th item contributes the weight $x_{i}.w_{i}$ to the total weight in the knapsack and profit $x_{i}.p_{i}$ to the total profit.

Hence, the objective of this algorithm is to

$$maximize\:\displaystyle\sum\limits_{n=1}^n (x_{i}.p_{}i)$$

subject to constraint,

$$\displaystyle\sum\limits_{n=1}^n (x_{i}.w_{}i) \leqslant W$$

It is clear that an optimal solution must fill the knapsack exactly, otherwise we could add a fraction of one of the remaining items and increase the overall profit.

Thus, an optimal solution can be obtained by

$$\displaystyle\sum\limits_{n=1}^n (x_{i}.w_{}i) = W$$

In this context, first we need to sort those items according to the value of $\frac{p_{i}}{w_{i}}$, so that $\frac{p_{i}+1}{w_{i}+1}$ ≤ $\frac{p_{i}}{w_{i}}$ . Here, x is an array to store the fraction of items.

Algorithm: Greedy-Fractional-Knapsack (w[1..n], p[1..n], W) 
for i = 1 to n 
   do x[i] = 0 
weight = 0 
for i = 1 to n 
   if weight + w[i] ≤ W then  
      x[i] = 1 
      weight = weight + w[i] 
   else 
      x[i] = (W - weight) / w[i] 
      weight = W 
      break 
return x

Analysis

If the provided items are already sorted into a decreasing order of $\mathbf{\frac{p_{i}}{w_{i}}}$, then the whileloop takes a time in O(n); Therefore, the total time including the sort is in O(n logn).

Example

Let us consider that the capacity of the knapsack W = 60 and the list of provided items are shown in the following table −

Item	A	B	C	D
Profit	280	100	120	120
Weight	40	10	20	24
Ratio $(\frac{p_{i}}{w_{i}})$	7	10	6	5

As the provided items are not sorted based on $\mathbf{\frac{p_{i}}{w_{i}}}$. After sorting, the items are as shown in the following table.

Item	B	A	C	D
Profit	100	280	120	120
Weight	10	40	20	24
Ratio $(\frac{p_{i}}{w_{i}})$	10	7	6	5

Solution

After sorting all the items according to $\frac{p_{i}}{w_{i}}$. First all of B is chosen as weight of B is less than the capacity of the knapsack. Next, item A is chosen, as the available capacity of the knapsack is greater than the weight of A. Now, C is chosen as the next item. However, the whole item cannot be chosen as the remaining capacity of the knapsack is less than the weight of C.

Hence, fraction of C (i.e. (60 − 50)/20) is chosen.

Now, the capacity of the Knapsack is equal to the selected items. Hence, no more item can be selected.

The total weight of the selected items is 10 + 40 + 20 * (10/20) = 60

And the total profit is 100 + 280 + 120 * (10/20) = 380 + 60 = 440

This is the optimal solution. We cannot gain more profit selecting any different combination of items.

Problem Statement

In job sequencing problem, the objective is to find a sequence of jobs, which is completed within their deadlines and gives maximum profit.

Solution

Let us consider, a set of n given jobs which are associated with deadlines and profit is earned, if a job is completed by its deadline. These jobs need to be ordered in such a way that there is maximum profit.

It may happen that all of the given jobs may not be completed within their deadlines.

Assume, deadline of i^th job J_i is d_i and the profit received from this job is p_i. Hence, the optimal solution of this algorithm is a feasible solution with maximum profit.

Thus, $D(i) > 0$ for $1 \leqslant i \leqslant n$.

Initially, these jobs are ordered according to profit, i.e. $p_{1} \geqslant p_{2} \geqslant p_{3} \geqslant \:... \: \geqslant p_{n}$.

Algorithm: Job-Sequencing-With-Deadline (D, J, n, k) 
D(0) := J(0) := 0 
k := 1 
J(1) := 1   // means first job is selected 
for i = 2 … n do 
   r := k 
   while D(J(r)) > D(i) and D(J(r)) ≠ r do 
      r := r – 1 
   if D(J(r)) ≤ D(i) and D(i) > r then 
      for l = k … r + 1 by -1 do 
         J(l + 1) := J(l) 
         J(r + 1) := i 
         k := k + 1

Analysis

In this algorithm, we are using two loops, one is within another. Hence, the complexity of this algorithm is $O(n^2)$.

Example

Let us consider a set of given jobs as shown in the following table. We have to find a sequence of jobs, which will be completed within their deadlines and will give maximum profit. Each job is associated with a deadline and profit.

Job	J1	J2	J3	J4	J5
Deadline	2	1	3	2	1
Profit	60	100	20	40	20

Solution

To solve this problem, the given jobs are sorted according to their profit in a descending order. Hence, after sorting, the jobs are ordered as shown in the following table.

Job	J2	J1	J4	J3	J5
Deadline	1	2	2	3	1
Profit	100	60	40	20	20

From this set of jobs, first we select J₂, as it can be completed within its deadline and contributes maximum profit.

• Next, J₁ is selected as it gives more profit compared to J₄.

• In the next clock, J₄ cannot be selected as its deadline is over, hence J₃ is selected as it executes within its deadline.

• The job J₅ is discarded as it cannot be executed within its deadline.

Thus, the solution is the sequence of jobs (J₂, J₁, J₃), which are being executed within their deadline and gives maximum profit.

Total profit of this sequence is 100 + 60 + 20 = 180.

Merge a set of sorted files of different length into a single sorted file. We need to find an optimal solution, where the resultant file will be generated in minimum time.

If the number of sorted files are given, there are many ways to merge them into a single sorted file. This merge can be performed pair wise. Hence, this type of merging is called as 2-way merge patterns.

As, different pairings require different amounts of time, in this strategy we want to determine an optimal way of merging many files together. At each step, two shortest sequences are merged.

To merge a p-record file and a q-record file requires possibly p + q record moves, the obvious choice being, merge the two smallest files together at each step.

Two-way merge patterns can be represented by binary merge trees. Let us consider a set of n sorted files {f₁, f₂, f₃, …, f_n}. Initially, each element of this is considered as a single node binary tree. To find this optimal solution, the following algorithm is used.

Algorithm: TREE (n)  
for i := 1 to n – 1 do  
   declare new node  
   node.leftchild := least (list) 
   node.rightchild := least (list) 
   node.weight) := ((node.leftchild).weight) + ((node.rightchild).weight)  
   insert (list, node);  
return least (list);

At the end of this algorithm, the weight of the root node represents the optimal cost.

Example

Let us consider the given files, f₁, f₂, f₃, f₄ and f₅ with 20, 30, 10, 5 and 30 number of elements respectively.

If merge operations are performed according to the provided sequence, then

M₁ = merge f₁ and f₂ => 20 + 30 = 50

M₂ = merge M₁ and f₃ => 50 + 10 = 60

M₃ = merge M₂ and f₄ => 60 + 5 = 65

M₄ = merge M₃ and f₅ => 65 + 30 = 95

Hence, the total number of operations is

50 + 60 + 65 + 95 = 270

Now, the question arises is there any better solution?

Mengurutkan angka sesuai dengan ukurannya dalam urutan menaik, kita mendapatkan urutan berikut -

f₄, f₃, f₁, f₂, f₅

Oleh karena itu, operasi penggabungan dapat dilakukan pada urutan ini

M₁ = merge f₄ and f₃ => 5 + 10 = 15

M₂ = merge M₁ and f₁ => 15 + 20 = 35

M₃ = merge M₂ and f₂ => 35 + 30 = 65

M₄ = merge M₃ and f₅ => 65 + 30 = 95

Oleh karena itu, jumlah operasi adalah

15 + 35 + 65 + 95 = 210

Jelas, ini lebih baik dari yang sebelumnya.

Dalam konteks ini, kami sekarang akan menyelesaikan masalah menggunakan algoritma ini.

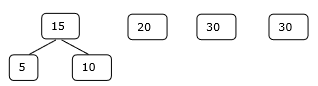
Set Awal

Langkah 1

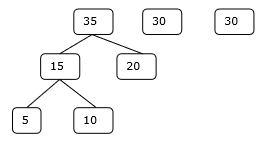
Langkah 2

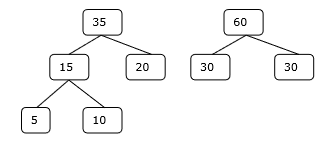
Langkah-3

Langkah-4

Oleh karena itu, penyelesaiannya membutuhkan jumlah perbandingan 15 + 35 + 60 + 95 = 205.

Pemrograman Dinamis juga digunakan dalam masalah pengoptimalan. Seperti metode divide-and-conquer, Pemrograman Dinamis memecahkan masalah dengan menggabungkan solusi dari submasalah. Selain itu, algoritma Pemrograman Dinamis memecahkan setiap sub-masalah hanya sekali dan kemudian menyimpan jawabannya dalam sebuah tabel, sehingga menghindari pekerjaan menghitung ulang jawaban setiap saat.

Dua sifat utama dari suatu masalah menunjukkan bahwa masalah yang diberikan dapat diselesaikan dengan menggunakan Pemrograman Dinamis. Properti ini adalahoverlapping sub-problems and optimal substructure.

Sub-Masalah yang Tumpang Tindih

Mirip dengan pendekatan Divide-and-Conquer, Pemrograman Dinamis juga menggabungkan solusi untuk sub-masalah. Ini terutama digunakan di mana solusi dari satu sub-masalah diperlukan berulang kali. Solusi yang dihitung disimpan dalam tabel, sehingga tidak perlu dihitung ulang. Oleh karena itu, teknik ini diperlukan jika ada sub-masalah yang tumpang tindih.

Misalnya, Pencarian Biner tidak memiliki sub-masalah yang tumpang tindih. Padahal program rekursif bilangan Fibonacci memiliki banyak sub masalah yang tumpang tindih.

Sub-Struktur Optimal

Masalah yang diberikan memiliki Properti Substruktur Optimal, jika solusi optimal dari masalah yang diberikan dapat diperoleh dengan menggunakan solusi optimal dari sub-masalah tersebut.

Misalnya, masalah Jalur Terpendek memiliki properti substruktur optimal berikut -

Jika sebuah node x terletak di jalur terpendek dari node sumber u ke node tujuan v, lalu jalur terpendek dari u untuk v adalah kombinasi jalur terpendek dari u untuk x, dan jalur terpendek dari x untuk v.

Algoritme All Pair Shortest Path standar seperti Floyd-Warshall dan Bellman-Ford adalah contoh khas dari Pemrograman Dinamis.

Langkah-Langkah Pendekatan Pemrograman Dinamis

Algoritma Pemrograman Dinamis dirancang menggunakan empat langkah berikut -

• Cirikan struktur solusi optimal.
• Tentukan nilai solusi optimal secara rekursif.
• Hitung nilai solusi optimal, biasanya dengan cara bottom-up.
• Buat solusi optimal dari informasi yang dihitung.

Aplikasi Pendekatan Pemrograman Dinamis

• Perkalian Rantai Matriks
• Urutan Umum Terpanjang
• Masalah Penjual Bepergian

Dalam tutorial ini, sebelumnya kita telah membahas masalah Fractional Knapsack dengan menggunakan pendekatan Greedy. Kami telah menunjukkan bahwa pendekatan Greedy memberikan solusi optimal untuk Fractional Knapsack. Namun, bab ini akan membahas masalah Knapsack 0-1 dan analisisnya.

Dalam Knapsack 0-1, item tidak bisa dipecahkan yang berarti pencuri harus mengambil item tersebut secara keseluruhan atau harus meninggalkannya. Inilah alasan dibalik menyebutnya sebagai Knapsack 0-1.

Oleh karena itu, dalam kasus Knapsack 0-1, nilai x_i bisa juga 0 atau 1, di mana batasan lainnya tetap sama.

0-1 Knapsack tidak bisa diselesaikan dengan pendekatan Greedy. Pendekatan serakah tidak menjamin solusi yang optimal. Dalam banyak kasus, pendekatan Greedy dapat memberikan solusi yang optimal.

Contoh berikut akan membentuk pernyataan kami.

Contoh 1

Mari kita pertimbangkan bahwa kapasitas ransel adalah W = 25 dan itemnya seperti yang ditunjukkan pada tabel berikut.

Barang	SEBUAH	B	C	D
Keuntungan	24	18	18	10
Bobot	24	10	10	7

Tanpa mempertimbangkan keuntungan per satuan berat (p_i/w_i), jika kita menerapkan pendekatan Greedy untuk menyelesaikan masalah ini, item pertama Aakan dipilih karena akan memberikan kontribusi max _i keuntungan ibu di antara semua elemen.

Setelah memilih item A, tidak ada lagi item yang akan dipilih. Oleh karena itu, untuk kumpulan item ini, total keuntungan adalah24. Sedangkan solusi optimal dapat dicapai dengan memilih item,B dan C, dimana total keuntungannya adalah 18 + 18 = 36.

Contoh-2

Alih-alih memilih item berdasarkan manfaat keseluruhan, dalam contoh ini item dipilih berdasarkan rasio p _i / w _i . Mari kita pertimbangkan bahwa kapasitas ransel adalah W = 60 dan itemnya seperti yang ditunjukkan pada tabel berikut.

Barang	SEBUAH	B	C
Harga	100	280	120
Bobot	10	40	20
Perbandingan	10	7	6

Menggunakan pendekatan Greedy, item pertama Adipilih. Lalu, item berikutnyaBterpilih. Karenanya, total keuntungan adalah100 + 280 = 380. Namun, solusi optimal dari contoh ini dapat dicapai dengan memilih item,B dan C, dimana keuntungan totalnya 280 + 120 = 400.

Dengan demikian, dapat disimpulkan bahwa pendekatan Greedy belum tentu memberikan solusi yang optimal.

Untuk menyelesaikan Knapsack 0-1, diperlukan pendekatan Dynamic Programming.

Pernyataan masalah

Seorang pencuri yang merampok toko dan dapat membawa max _i berat mal dariWke ranselnya. Adan barang dan berat i^th item adalah w_i dan keuntungan memilih item ini p_i. Barang apa yang harus diambil pencuri?

Pendekatan Pemrograman Dinamis

Membiarkan i menjadi item dengan nomor tertinggi dalam solusi optimal S untuk Wdolar. KemudianS^' = S - {i} adalah solusi optimal untuk W - w_i dolar dan nilai solusi S adalah V_i ditambah nilai sub-masalah.

Fakta ini dapat kita ekspresikan dalam rumus berikut: define c[i, w] menjadi solusi untuk barang 1,2, … , idan max _i berat badan ibuw.

Algoritme mengambil masukan berikut

• Max _i berat badan ibuW

• Jumlah item n

• Dua urutan v = <v₁, v₂, …, v_n> dan w = <w₁, w₂, …, w_n>

Dynamic-0-1-knapsack (v, w, n, W) 
for w = 0 to W do 
   c[0, w] = 0 
for i = 1 to n do 
   c[i, 0] = 0 
   for w = 1 to W do 
      if wi ≤ w then 
         if vi + c[i-1, w-wi] then 
            c[i, w] = vi + c[i-1, w-wi] 
         else c[i, w] = c[i-1, w] 
      else 
         c[i, w] = c[i-1, w]

Kumpulan item yang akan diambil dapat disimpulkan dari tabel, mulai dari c[n, w] dan menelusuri ke belakang dari mana nilai optimal berasal.

Jika c [i, w] = c [i-1, w] , maka itemi bukan bagian dari solusi, dan kami terus menelusuri c[i-1, w]. Jika tidak, itemi adalah bagian dari solusi, dan kami terus menelusuri c[i-1, w-W].

Analisis

Algoritma ini membutuhkan θ ( n , w ) kali karena tabel c memiliki entri ( n + 1). ( W + 1), di mana setiap entri membutuhkan θ (1) waktu untuk menghitung.

Masalah urutan terpanjang adalah menemukan urutan terpanjang yang ada di kedua string yang diberikan.

Urutan

Mari kita pertimbangkan urutan S = <s ₁ , s ₂ , s ₃ , s ₄ ,…, s _n >.

Sebuah barisan Z = <z ₁ , z ₂ , z ₃ , z ₄ ,…, z _m > di atas S disebut deretan S, jika dan hanya jika itu dapat diturunkan dari penghapusan S beberapa elemen.

Urutan Umum

Seharusnya, X dan Yadalah dua urutan di atas satu set elemen yang terbatas. Kita bisa bilang begituZ adalah kelanjutan umum dari X dan Y, jika Z adalah kelanjutan dari keduanya X dan Y.

Urutan Umum Terpanjang

Jika satu set urutan diberikan, masalah urutan terpanjang adalah menemukan urutan yang sama dari semua urutan yang memiliki panjang maksimal.

Masalah lanjutan umum terpanjang adalah masalah ilmu komputer klasik, dasar dari program perbandingan data seperti utilitas-diff, dan memiliki aplikasi dalam bioinformatika. Ini juga banyak digunakan oleh sistem kontrol revisi, seperti SVN dan Git, untuk merekonsiliasi beberapa perubahan yang dibuat pada kumpulan file yang dikontrol revisi.

Metode Naif

Membiarkan X menjadi urutan panjang m dan Y urutan panjang n. Periksa setiap kelanjutan dariX apakah itu kelanjutan dari Y, dan mengembalikan urutan umum terpanjang yang ditemukan.

Ada 2^m selanjutnya dari X. Menguji urutan apakah itu merupakan kelanjutan dariY mengambil O(n)waktu. Dengan demikian, algoritma naif akan mengambilO(n2^m) waktu.

Pemrograman Dinamis

Misalkan X = <x ₁ , x ₂ , x ₃ ,…, x _m > dan Y = <y ₁ , y ₂ , y ₃ ,…, y _n > menjadi barisan. Untuk menghitung panjang elemen digunakan algoritma berikut.

Dalam prosedur ini, tabel C[m, n] dihitung dalam urutan mayor baris dan tabel lain B[m,n] dihitung untuk membangun solusi optimal.

Algorithm: LCS-Length-Table-Formulation (X, Y)
m := length(X) 
n := length(Y) 
for i = 1 to m do 
   C[i, 0] := 0 
for j = 1 to n do 
   C[0, j] := 0 
for i = 1 to m do 
   for j = 1 to n do 
      if xi = yj 
         C[i, j] := C[i - 1, j - 1] + 1 
         B[i, j] := ‘D’ 
      else 
         if C[i -1, j] ≥ C[i, j -1] 
            C[i, j] := C[i - 1, j] + 1 
            B[i, j] := ‘U’ 
         else 
         C[i, j] := C[i, j - 1]
         B[i, j] := ‘L’ 
return C and B

Algorithm: Print-LCS (B, X, i, j)
if i = 0 and j = 0 
   return  
if B[i, j] = ‘D’ 
   Print-LCS(B, X, i-1, j-1) 
   Print(xi) 
else if B[i, j] = ‘U’ 
   Print-LCS(B, X, i-1, j) 
else 
   Print-LCS(B, X, i, j-1)

Algoritme ini akan mencetak urutan umum terpanjang X dan Y.

Analisis

Untuk mengisi tabel, bagian luar for perulangan berulang m waktu dan batin for perulangan berulang nwaktu. Oleh karena itu, kompleksitas algoritme adalah O (m, n) , di manam dan n adalah panjang dua senar.

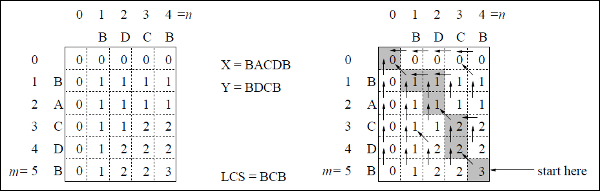
Contoh

Dalam contoh ini, kami memiliki dua string X = BACDB dan Y = BDCB untuk menemukan urutan persekutuan terpanjang.

Mengikuti algoritma LCS-Length-Table-Formulation (seperti yang dinyatakan di atas), kami telah menghitung tabel C (ditampilkan di sisi kiri) dan tabel B (ditampilkan di sisi kanan).

Dalam tabel B, alih-alih 'D', 'L' dan 'U', kami masing-masing menggunakan panah diagonal, panah kiri, dan panah atas. Setelah menghasilkan tabel B, LCS ditentukan oleh fungsi LCS-Print. Hasilnya adalah BCB.

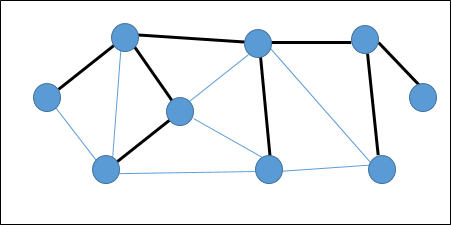
SEBUAH spanning tree adalah himpunan bagian dari Graph yang tidak diarahkan yang memiliki semua simpul yang terhubung dengan jumlah sisi minimum.

Jika semua simpul terhubung dalam sebuah grafik, maka terdapat setidaknya satu pohon bentang. Dalam grafik, mungkin ada lebih dari satu pohon rentang.

Properti

• Pohon perentang tidak memiliki siklus apa pun.
• Titik manapun dapat dicapai dari simpul lainnya.

Contoh

Dalam grafik berikut, tepi yang disorot membentuk pohon rentang.

Pohon Rentang Minimum

SEBUAH Minimum Spanning Tree (MST)adalah himpunan bagian tepi dari graf tak berarah berbobot terhubung yang menghubungkan semua simpul bersama dengan bobot tepi total minimum yang mungkin. Untuk mendapatkan MST, dapat digunakan algoritma Prim atau algoritma Kruskal. Karenanya, kita akan membahas algoritma Prim di bab ini.

Seperti yang telah kita diskusikan, satu grafik mungkin memiliki lebih dari satu pohon rentang. Jika adan jumlah simpul, pohon rentang harus memiliki n - 1jumlah tepi. Dalam konteks ini, jika setiap tepi grafik dikaitkan dengan bobot dan terdapat lebih dari satu pohon rentang, kita perlu mencari pohon rentang minimum dari grafik.

Selain itu, jika ada duplikat tepi berbobot, grafik mungkin memiliki beberapa pohon rentang minimum.

Pada grafik di atas, kami telah menunjukkan pohon rentang meskipun itu bukan pohon rentang minimum. Biaya pohon perentang ini adalah (5 + 7 + 3 + 3 + 5 + 8 + 3 + 4) = 38.

Kami akan menggunakan algoritma Prim untuk menemukan pohon rentang minimum.

Algoritma Prim

Algoritme Prim adalah pendekatan serakah untuk menemukan pohon rentang minimum. Dalam algoritma ini, untuk membentuk MST kita bisa mulai dari simpul sembarang.

Algorithm: MST-Prim’s (G, w, r) 
for each u є G.V 
   u.key = ∞ 
   u.∏ = NIL 
r.key = 0 
Q = G.V 
while Q ≠ Ф 
   u = Extract-Min (Q) 
   for each v є G.adj[u] 
      if each v є Q and w(u, v) < v.key 
         v.∏ = u 
         v.key = w(u, v)

Fungsi Extract-Min mengembalikan simpul dengan biaya tepi minimum. Fungsi ini bekerja pada min-heap.

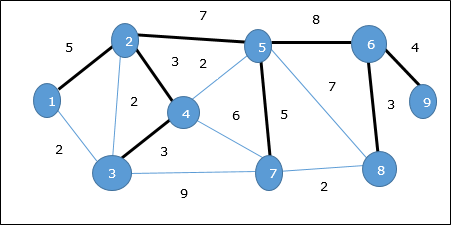
Contoh

Menggunakan algoritma Prim, kita bisa mulai dari simpul manapun, mari kita mulai dari simpul 1.

Puncak 3 terhubung ke simpul 1 dengan biaya tepi minimum, maka tepi (1, 2) ditambahkan ke pohon rentang.

Selanjutnya, tepi (2, 3) dianggap karena ini adalah minimum di antara edge {(1, 2), (2, 3), (3, 4), (3, 7)}.

Pada langkah selanjutnya, kita mendapatkan keunggulan (3, 4) dan (2, 4)dengan biaya minimum. Tepi(3, 4) dipilih secara acak.

Dengan cara yang sama, tepian (4, 5), (5, 7), (7, 8), (6, 8) dan (6, 9)dipilih. Karena semua simpul dikunjungi, sekarang algoritme berhenti.

Biaya pohon bentang adalah (2 + 2 + 3 + 2 + 5 + 2 + 3 + 4) = 23. Tidak ada lagi pohon bentang dalam grafik ini dengan biaya kurang dari 23.

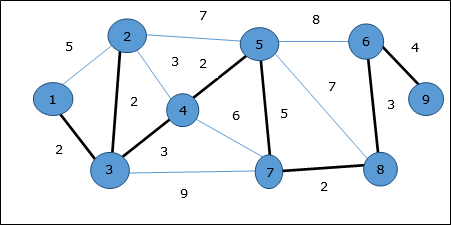
Algoritma Dijkstra

Algoritma Dijkstra memecahkan masalah jalur terpendek sumber tunggal pada graf berbobot terarah G = (V, E) , di mana semua sisi non-negatif (yaitu, w (u, v) ≥ 0 untuk setiap sisi (u, v ) Є E ).

Dalam algoritma berikut, kita akan menggunakan satu fungsi Extract-Min(), yang mengekstrak node dengan kunci terkecil.

Algorithm: Dijkstra’s-Algorithm (G, w, s) 
for each vertex v Є G.V  
   v.d := ∞ 
   v.∏ := NIL 
s.d := 0 
S := Ф 
Q := G.V 
while Q ≠ Ф 
   u := Extract-Min (Q) 
   S := S U {u} 
   for each vertex v Є G.adj[u] 
      if v.d > u.d + w(u, v) 
         v.d := u.d + w(u, v) 
         v.∏ := u

Analisis

Kompleksitas algoritma ini sepenuhnya bergantung pada implementasi fungsi Extract-Min. Jika fungsi ekstrak min diimplementasikan menggunakan pencarian linier, kompleksitas algoritma ini adalahO(V² + E).

Dalam algoritma ini, jika kita menggunakan min-heap di mana Extract-Min() fungsi berfungsi untuk mengembalikan node dari Q dengan kunci terkecil, kompleksitas algoritma ini dapat dikurangi lebih jauh.

Contoh

Mari kita pertimbangkan titik 1 dan 9sebagai titik awal dan tujuan masing-masing. Awalnya, semua simpul kecuali simpul awal ditandai dengan ∞ dan simpul awal ditandai dengan0.

Puncak	Awal	Langkah1 V 1	Langkah2 V 3	Langkah3 V 2	Langkah4 V 4	Langkah5 V 5	Langkah6 V 7	Langkah7 V 8	Langkah8 V 6
1	0	0	0	0	0	0	0	0	0
2	∞	5	4	4	4	4	4	4	4
3	∞	2	2	2	2	2	2	2	2
4	∞	∞	∞	7	7	7	7	7	7
5	∞	∞	∞	11	9	9	9	9	9
6	∞	∞	∞	∞	∞	17	17	16	16
7	∞	∞	11	11	11	11	11	11	11
8	∞	∞	∞	∞	∞	16	13	13	13
9	∞	∞	∞	∞	∞	∞	∞	∞	20

Oleh karena itu, jarak minimum simpul 9 dari puncak 1 adalah 20. Dan jalannya adalah

1 → 3 → 7 → 8 → 6 → 9

Jalur ini ditentukan berdasarkan informasi pendahulu.

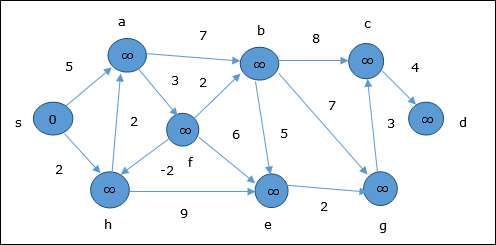
Algoritma Bellman Ford

Algoritme ini memecahkan masalah jalur terpendek sumber tunggal dari grafik berarah G = (V, E)di mana bobot tepinya mungkin negatif. Selain itu, algoritma ini dapat diterapkan untuk menemukan jalur terpendek, jika tidak ada siklus berbobot negatif.

Algorithm: Bellman-Ford-Algorithm (G, w, s) 
for each vertex v Є G.V  
   v.d := ∞ 
   v.∏ := NIL 
s.d := 0 
for i = 1 to |G.V| - 1 
   for each edge (u, v) Є G.E 
      if v.d > u.d + w(u, v) 
         v.d := u.d +w(u, v) 
         v.∏ := u 
for each edge (u, v) Є G.E 
   if v.d > u.d + w(u, v) 
      return FALSE 
return TRUE

Analisis

Pertama for loop digunakan untuk inisialisasi, yang berjalan di O(V)waktu. Selanjutnyafor putaran berjalan |V - 1| melewati tepi, yang mengambilO(E) waktu.

Karenanya, algoritme Bellman-Ford berjalan O(V, E) waktu.

Contoh

Contoh berikut menunjukkan cara kerja algoritma Bellman-Ford selangkah demi selangkah. Grafik ini memiliki sisi negatif tetapi tidak memiliki siklus negatif, maka masalahnya dapat diselesaikan dengan menggunakan teknik ini.

Pada saat inisialisasi, semua simpul kecuali sumber ditandai dengan ∞ dan sumber ditandai dengan 0.

Pada langkah pertama, semua simpul yang dapat dijangkau dari sumber diperbarui dengan biaya minimum. Oleh karena itu, simpula dan h diperbarui.

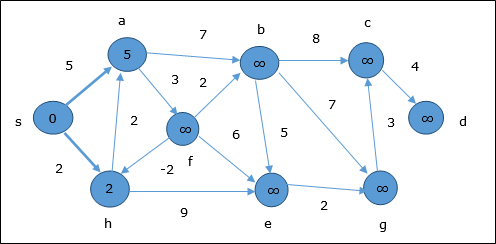
Pada langkah selanjutnya, simpul a, b, f dan e diperbarui.

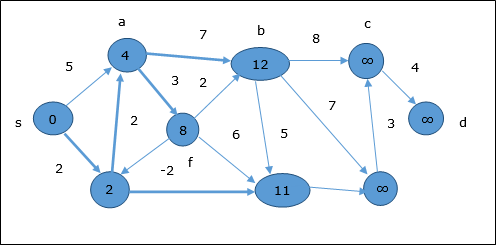
Mengikuti logika yang sama, di simpul langkah ini b, f, c dan g diperbarui.

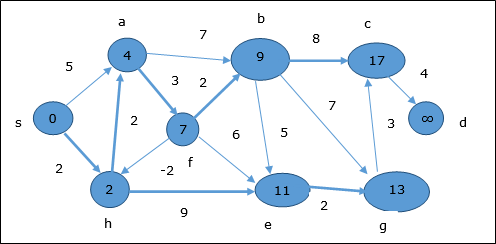
Di sini, simpul c dan d diperbarui.

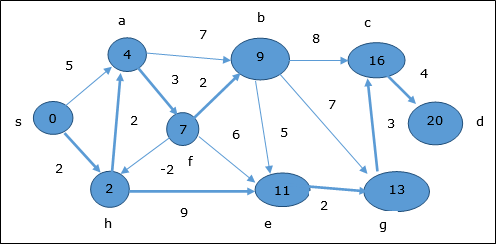
Oleh karena itu, jarak minimum antar simpul s dan simpul d adalah 20.

Berdasarkan informasi pendahulu, jalurnya adalah s → h → e → g → c → d

Grafik bertingkat G = (V, E) adalah grafik berarah tempat simpul dipartisi k (dimana k > 1) jumlah subset yang terputus-putus S = {s₁,s₂,…,s_k}sehingga tepi (u, v) ada di E, lalu u Є s _i dan v Є s _{1 + 1} untuk beberapa subset di partisi dan |s₁| = |s_k| = 1.

Titik puncak s Є s₁ disebut source dan puncak t Є s_k disebut sink.

Gbiasanya diasumsikan sebagai grafik berbobot. Dalam grafik ini, biaya sebuah sisi (i, j) diwakili oleh c (i, j) . Oleh karena itu, biaya jalur dari sumbers tenggelam t adalah jumlah biaya dari setiap sisi di jalur ini.

Masalah grafik multistage adalah menemukan jalur dengan biaya minimum dari sumber s tenggelam t.

Contoh

Perhatikan contoh berikut untuk memahami konsep grafik bertingkat.

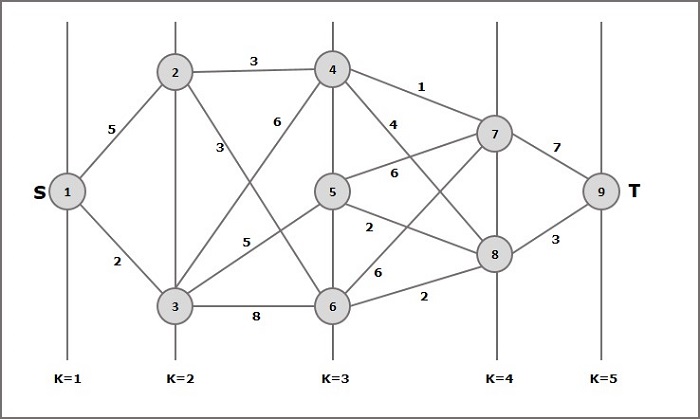
Menurut rumusnya, kita harus menghitung biayanya (i, j) menggunakan langkah-langkah berikut

Langkah-1: Biaya (K-2, j)

Pada langkah ini, tiga node (node ​​4, 5. 6) dipilih sebagai j. Karenanya, kami memiliki tiga opsi untuk memilih biaya minimum pada langkah ini.

Biaya (3, 4) = min {c (4, 7) + Biaya (7, 9), c (4, 8) + Biaya (8, 9)} = 7

Biaya (3, 5) = min {c (5, 7) + Biaya (7, 9), c (5, 8) + Biaya (8, 9)} = 5

Biaya (3, 6) = min {c (6, 7) + Biaya (7, 9), c (6, 8) + Biaya (8, 9)} = 5

Langkah-2: Biaya (K-3, j)

Dipilih dua buah titik sebagai j karena pada tahap k - 3 = 2 terdapat dua buah titik yaitu 2 dan 3. Jadi nilai i = 2 dan j = 2 dan 3.

Biaya (2, 2) = min {c (2, 4) + Biaya (4, 8) + Biaya (8, 9), c (2, 6) +

Biaya (6, 8) + Biaya (8, 9)} = 8

Biaya (2, 3) = {c (3, 4) + Biaya (4, 8) + Biaya (8, 9), c (3, 5) + Biaya (5, 8) + Biaya (8, 9), c (3, 6) + Biaya (6, 8) + Biaya (8, 9)} = 10

Langkah-3: Biaya (K-4, j)

Biaya (1, 1) = {c (1, 2) + Biaya (2, 6) + Biaya (6, 8) + Biaya (8, 9), c (1, 3) + Biaya (3, 5) + Biaya (5, 8) + Biaya (8, 9))} = 12

c (1, 3) + Biaya (3, 6) + Biaya (6, 8 + Biaya (8, 9))} = 13

Karenanya, jalur yang memiliki biaya minimum adalah 1→ 3→ 5→ 8→ 9.

Pernyataan masalah

Seorang pelancong perlu mengunjungi semua kota dari daftar, di mana jarak antara semua kota diketahui dan setiap kota harus dikunjungi hanya sekali. Rute terpendek apa yang dia kunjungi setiap kota tepat satu kali dan kembali ke kota asal?

Larutan

Masalah penjual keliling adalah masalah komputasi yang paling terkenal. Kita dapat menggunakan pendekatan brute-force untuk mengevaluasi setiap kemungkinan tur dan memilih yang terbaik. Untukn jumlah simpul dalam grafik, ada (n - 1)! sejumlah kemungkinan.

Alih-alih brute-force menggunakan pendekatan pemrograman dinamis, solusi dapat diperoleh dalam waktu yang lebih singkat, meskipun tidak ada algoritma waktu polinomial.

Mari kita perhatikan grafik G = (V, E), dimana V adalah sekumpulan kota dan Eadalah satu set tepi berbobot. Sebuah pinggire(u, v) mewakili simpul itu u dan vterhubung. Jarak antar titiku dan v adalah d(u, v), yang seharusnya tidak negatif.

Misalkan kita sudah mulai di kota 1 dan setelah mengunjungi beberapa kota sekarang kita berada di kota j. Karenanya, ini adalah tur parsial. Kami tentu perlu tahuj, karena ini akan menentukan kota mana yang paling nyaman untuk dikunjungi selanjutnya. Kita juga perlu mengetahui semua kota yang dikunjungi selama ini, agar tidak terulang lagi. Oleh karena itu, ini adalah sub-masalah yang sesuai.

Untuk subset kota S Є {1, 2, 3, ... , n} itu termasuk 1, dan j Є S, biarkan C(S, j) menjadi panjang jalur terpendek yang mengunjungi setiap node S tepat sekali, mulai dari 1 dan berakhir pada j.

Kapan |S| > 1, kita definisikanC(S, 1) = ∝ karena jalur tidak bisa dimulai dan diakhiri 1.

Sekarang, mari kita ekspresikan C(S, j)dalam hal sub-masalah yang lebih kecil. Kita harus mulai1 dan diakhiri pada j. Kita harus memilih kota berikutnya sedemikian rupa

$$C(S, j) = min \:C(S - \lbrace j \rbrace, i) + d(i, j)\:where\: i\in S \: and\: i \neq jc(S, j) = minC(s- \lbrace j \rbrace, i)+ d(i,j) \:where\: i\in S \: and\: i \neq j $$

Algorithm: Traveling-Salesman-Problem 
C ({1}, 1) = 0 
for s = 2 to n do 
   for all subsets S Є {1, 2, 3, … , n} of size s and containing 1 
      C (S, 1) = ∞ 
   for all j Є S and j ≠ 1 
      C (S, j) = min {C (S – {j}, i) + d(i, j) for i Є S and i ≠ j} 
Return minj C ({1, 2, 3, …, n}, j) + d(j, i)

Analisis

Ada paling banyak $2^n.n$sub-masalah dan masing-masing membutuhkan waktu linier untuk menyelesaikannya. Oleh karena itu, total waktu berjalan adalah$O(2^n.n^2)$.

Contoh

Dalam contoh berikut, kami akan mengilustrasikan langkah-langkah untuk menyelesaikan masalah penjual keliling.

Dari grafik di atas, disiapkan tabel berikut.

	1	2	3	4
1	0	10	15	20
2	5	0	9	10
3	6	13	0	12
4	8	8	9	0

S = Φ

$$\small Cost (2,\Phi,1) = d (2,1) = 5\small Cost(2,\Phi,1)=d(2,1)=5$$

$$\small Cost (3,\Phi,1) = d (3,1) = 6\small Cost(3,\Phi,1)=d(3,1)=6$$

$$\small Cost (4,\Phi,1) = d (4,1) = 8\small Cost(4,\Phi,1)=d(4,1)=8$$

S = 1

$$\small Cost (i,s) = min \lbrace Cost (j,s – (j)) + d [i,j]\rbrace\small Cost (i,s)=min \lbrace Cost (j,s)-(j))+ d [i,j]\rbrace$$

$$\small Cost (2,\lbrace 3 \rbrace,1) = d [2,3] + Cost (3,\Phi,1) = 9 + 6 = 15cost(2,\lbrace3 \rbrace,1)=d[2,3]+cost(3,\Phi ,1)=9+6=15$$

$$\small Cost (2,\lbrace 4 \rbrace,1) = d [2,4] + Cost (4,\Phi,1) = 10 + 8 = 18cost(2,\lbrace4 \rbrace,1)=d[2,4]+cost(4,\Phi,1)=10+8=18$$

$$\small Cost (3,\lbrace 2 \rbrace,1) = d [3,2] + Cost (2,\Phi,1) = 13 + 5 = 18cost(3,\lbrace2 \rbrace,1)=d[3,2]+cost(2,\Phi,1)=13+5=18$$

$$\small Cost (3,\lbrace 4 \rbrace,1) = d [3,4] + Cost (4,\Phi,1) = 12 + 8 = 20cost(3,\lbrace4 \rbrace,1)=d[3,4]+cost(4,\Phi,1)=12+8=20$$

$$\small Cost (4,\lbrace 3 \rbrace,1) = d [4,3] + Cost (3,\Phi,1) = 9 + 6 = 15cost(4,\lbrace3 \rbrace,1)=d[4,3]+cost(3,\Phi,1)=9+6=15$$

$$\small Cost (4,\lbrace 2 \rbrace,1) = d [4,2] + Cost (2,\Phi,1) = 8 + 5 = 13cost(4,\lbrace2 \rbrace,1)=d[4,2]+cost(2,\Phi,1)=8+5=13$$

S = 2

$$\small Cost(2, \lbrace 3, 4 \rbrace, 1)=\begin{cases}d[2, 3] + Cost(3, \lbrace 4 \rbrace, 1) = 9 + 20 = 29\\d[2, 4] + Cost(4, \lbrace 3 \rbrace, 1) = 10 + 15 = 25=25\small Cost (2,\lbrace 3,4 \rbrace,1)\\\lbrace d[2,3]+ \small cost(3,\lbrace4\rbrace,1)=9+20=29d[2,4]+ \small Cost (4,\lbrace 3 \rbrace ,1)=10+15=25\end{cases}= 25$$

$$\small Cost(3, \lbrace 2, 4 \rbrace, 1)=\begin{cases}d[3, 2] + Cost(2, \lbrace 4 \rbrace, 1) = 13 + 18 = 31\\d[3, 4] + Cost(4, \lbrace 2 \rbrace, 1) = 12 + 13 = 25=25\small Cost (3,\lbrace 2,4 \rbrace,1)\\\lbrace d[3,2]+ \small cost(2,\lbrace4\rbrace,1)=13+18=31d[3,4]+ \small Cost (4,\lbrace 2 \rbrace ,1)=12+13=25\end{cases}= 25$$

$$\small Cost(4, \lbrace 2, 3 \rbrace, 1)=\begin{cases}d[4, 2] + Cost(2, \lbrace 3 \rbrace, 1) = 8 + 15 = 23\\d[4, 3] + Cost(3, \lbrace 2 \rbrace, 1) = 9 + 18 = 27=23\small Cost (4,\lbrace 2,3 \rbrace,1)\\\lbrace d[4,2]+ \small cost(2,\lbrace3\rbrace,1)=8+15=23d[4,3]+ \small Cost (3,\lbrace 2 \rbrace ,1)=9+18=27\end{cases}= 23$$

S = 3

$$\small Cost(1, \lbrace 2, 3, 4 \rbrace, 1)=\begin{cases}d[1, 2] + Cost(2, \lbrace 3, 4 \rbrace, 1) = 10 + 25 = 35\\d[1, 3] + Cost(3, \lbrace 2, 4 \rbrace, 1) = 15 + 25 = 40\\d[1, 4] + Cost(4, \lbrace 2, 3 \rbrace, 1) = 20 + 23 = 43=35 cost(1,\lbrace 2,3,4 \rbrace),1)\\d[1,2]+cost(2,\lbrace 3,4 \rbrace,1)=10+25=35\\d[1,3]+cost(3,\lbrace 2,4 \rbrace,1)=15+25=40\\d[1,4]+cost(4,\lbrace 2,3 \rbrace ,1)=20+23=43=35\end{cases}$$

Jalur biaya minimum adalah 35.

Mulai dari biaya {1, {2, 3, 4}, 1}, kami mendapatkan nilai minimum untuk d [1, 2]. Kapans = 3, pilih jalur dari 1 ke 2 (biayanya 10) lalu mundur. Kapans = 2, kami mendapatkan nilai minimum untuk d [4, 2]. Pilih jalur dari 2 hingga 4 (biaya 10) lalu mundur.

Kapan s = 1, kami mendapatkan nilai minimum untuk d [4, 3]. Memilih jalur 4 ke 3 (biaya 9), lalu kita akan pergi ke lalu pergi kes = Φlangkah. Kami mendapatkan nilai minimum untukd [3, 1] (biayanya 6).

Binary Search Tree (BST) adalah pohon tempat nilai-nilai kunci disimpan di node internal. Node eksternal adalah node nol. Kunci diurutkan secara leksikografis, yaitu untuk setiap node internal semua kunci di sub-pohon kiri lebih kecil dari kunci di node, dan semua kunci di sub-pohon kanan lebih besar.

Ketika kita mengetahui frekuensi pencarian setiap kunci, cukup mudah untuk menghitung biaya yang diharapkan untuk mengakses setiap node di pohon. Pohon pencarian biner yang optimal adalah BST, yang memiliki biaya minimal yang diharapkan untuk menemukan setiap node

Waktu pencarian elemen dalam BST adalah O(n), sedangkan dalam waktu pencarian Balanced-BST adalah O(log n). Sekali lagi waktu pencarian dapat ditingkatkan dalam Pohon Pencarian Biner Biaya Optimal, menempatkan data yang paling sering digunakan di root dan lebih dekat ke elemen root, sambil menempatkan data yang paling jarang digunakan di dekat daun dan daun.

Di sini, Algoritma Pohon Pencarian Biner Optimal disajikan. Pertama, kami membangun BST dari satu set yang disediakann jumlah kunci yang berbeda < k₁, k₂, k₃, ... k_n >. Di sini kami berasumsi, kemungkinan mengakses kunciK_i adalah p_i. Beberapa kunci boneka (d₀, d₁, d₂, ... d_n) ditambahkan karena beberapa pencarian dapat dilakukan untuk nilai-nilai yang tidak ada dalam kumpulan Kunci K. Kami berasumsi, untuk setiap kunci dummyd_i kemungkinan akses adalah q_i.

Optimal-Binary-Search-Tree(p, q, n) 
e[1…n + 1, 0…n],  
w[1…n + 1, 0…n], 
root[1…n + 1, 0…n]  
for i = 1 to n + 1 do 
   e[i, i - 1] := qi - 1 
   w[i, i - 1] := qi - 1  
for l = 1 to n do 
   for i = 1 to n – l + 1 do 
      j = i + l – 1 e[i, j] := ∞ 
      w[i, i] := w[i, i -1] + pj + qj 
      for r = i to j do 
         t := e[i, r - 1] + e[r + 1, j] + w[i, j] 
         if t < e[i, j] 
            e[i, j] := t 
            root[i, j] := r 
return e and root

Analisis

Algoritme membutuhkan O (n³) waktu, sejak tiga bersarang forloop digunakan. Masing-masing loop ini mengambil paling banyakn nilai-nilai.

Contoh

Mempertimbangkan pohon berikut, biayanya 2,80, meskipun ini bukan hasil yang optimal.

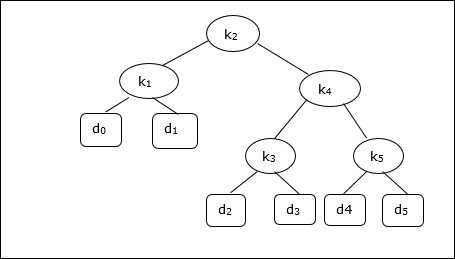
Node	Kedalaman	Kemungkinan	Kontribusi
k 1	1	0.15	0.30
k 2	0	0.10	0.10
k 3	2	0,05	0.15
k 4	1	0.10	0.20
k 5	2	0.20	0.60
d 0	2	0,05	0.15
d 1	2	0.10	0.30
d 2	3	0,05	0.20
d 3	3	0,05	0.20
d 4	3	0,05	0.20
d 5	3	0.10	0.40
Total			2.80

Untuk mendapatkan solusi yang optimal, dengan menggunakan algoritma yang dibahas dalam bab ini, tabel berikut dibuat.

Dalam tabel berikut, indeks kolom adalah i dan indeks baris adalah j.

e	1	2	3	4	5	6
5	2.75	2.00	1.30	0.90	0,50	0.10
4	1.75	1.20	0.60	0.30	0,05
3	1.25	0.70	0.25	0,05
2	0.90	0.40	0,05
1	0.45	0.10
0	0,05

w	1	2	3	4	5	6
5	1.00	0.80	0.60	0,50	0.35	0.10
4	0.70	0,50	0.30	0.20	0,05
3	0,55	0.35	0.15	0,05
2	0.45	0.25	0,05
1	0.30	0.10
0	0,05

akar	1	2	3	4	5
5	2	4	5	5	5
4	2	2	4	4
3	2	2	3
2	1	2
1	1

Dari tabel-tabel ini, pohon yang optimal dapat dibentuk.

Ada beberapa jenis heap, namun pada bab ini kita akan membahas heap biner. SEBUAHbinary heapadalah struktur data, yang terlihat mirip dengan pohon biner lengkap. Struktur data heap mematuhi properti pengurutan yang dibahas di bawah ini. Umumnya, Heap diwakili oleh sebuah array. Dalam bab ini, kami merepresentasikan heap olehH.

Karena elemen heap disimpan dalam array, dengan mempertimbangkan indeks awal sebagai 1, posisi simpul induk dari i^th elemen dapat ditemukan di ⌊ i/2 ⌋. Anak kiri dan anak kanani^th node berada di posisi 2i dan 2i + 1.

Heap biner dapat diklasifikasikan lebih lanjut sebagai a max-heap atau a min-heap berdasarkan properti pemesanan.

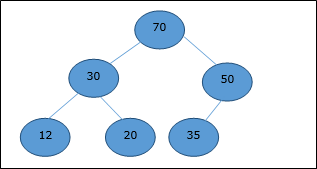
Max-Heap

Di heap ini, nilai kunci node lebih besar dari atau sama dengan nilai kunci turunan tertinggi.

Karenanya, H[Parent(i)] ≥ H[i]

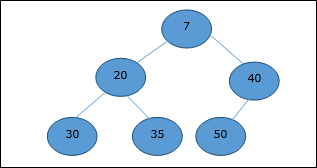
Min-Heap

Di mean-heap, nilai kunci sebuah node lebih kecil dari atau sama dengan nilai kunci dari turunan terendah.

Karenanya, H[Parent(i)] ≤ H[i]

Dalam konteks ini, operasi dasar ditunjukkan di bawah ini sehubungan dengan Max-Heap. Penyisipan dan penghapusan elemen di dalam dan dari heaps membutuhkan penataan ulang elemen. Karenanya,Heapify fungsi perlu dipanggil.

Representasi Array

Pohon biner lengkap dapat diwakili oleh larik, menyimpan elemennya menggunakan traversal urutan tingkat.

Mari kita pertimbangkan heap (seperti yang ditunjukkan di bawah) yang akan diwakili oleh sebuah array H.

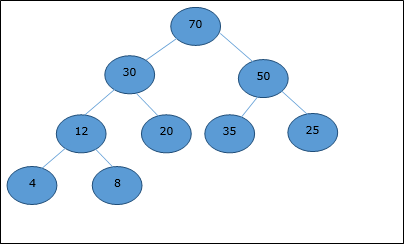
Mempertimbangkan indeks awal sebagai 0, menggunakan traversal urutan tingkat, elemen disimpan dalam larik sebagai berikut.

Index	0	1	2	3	4	5	6	7	8	...
elements	70	30	50	12	20	35	25	4	8	...

Dalam konteks ini, operasi pada heap direpresentasikan sehubungan dengan Max-Heap.

Untuk menemukan indeks induk dari suatu elemen pada indeks i, algoritma berikut Parent (numbers[], i) digunakan.

Algorithm: Parent (numbers[], i) 
if i == 1 
   return NULL 
else 
   [i / 2]

Indeks anak kiri dari sebuah elemen di index i dapat ditemukan menggunakan algoritma berikut, Left-Child (numbers[], i).

Algorithm: Left-Child (numbers[], i) 
If 2 * i ≤ heapsize 
   return [2 * i] 
else 
   return NULL

Indeks anak kanan dari suatu elemen di indeks i dapat ditemukan menggunakan algoritma berikut, Right-Child(numbers[], i).

Algorithm: Right-Child (numbers[], i) 
if 2 * i < heapsize 
   return [2 * i + 1] 
else 
   return NULL

Untuk menyisipkan elemen di heap, elemen baru awalnya ditambahkan ke akhir heap sebagai elemen terakhir dari array.

Setelah memasukkan elemen ini, properti heap mungkin dilanggar, oleh karena itu properti heap diperbaiki dengan membandingkan elemen yang ditambahkan dengan induknya dan memindahkan elemen yang ditambahkan ke atas satu tingkat, bertukar posisi dengan induknya. Proses ini disebutpercolation up.

Perbandingan diulang sampai induk lebih besar dari atau sama dengan elemen perkolasi.

Algorithm: Max-Heap-Insert (numbers[], key) 
heapsize = heapsize + 1 
numbers[heapsize] = -∞ 
i = heapsize 
numbers[i] = key 
while i > 1 and numbers[Parent(numbers[], i)] < numbers[i] 
   exchange(numbers[i], numbers[Parent(numbers[], i)]) 
   i = Parent (numbers[], i)

Analisis

Awalnya, elemen ditambahkan di akhir larik. Jika melanggar properti heap, elemen tersebut akan ditukar dengan induknya. Tinggi pohon itulog n. Maksimumlog n jumlah operasi perlu dilakukan.

Oleh karena itu, kompleksitas fungsi ini O(log n).

Contoh

Mari kita pertimbangkan max-heap, seperti yang ditunjukkan di bawah ini, di mana elemen baru 5 perlu ditambahkan.

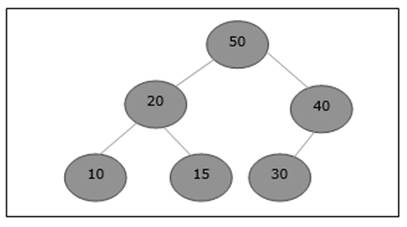
Awalnya, 55 akan ditambahkan di akhir larik ini.

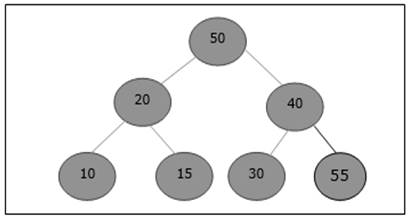
Setelah penyisipan, ini melanggar properti heap. Karenanya, elemen perlu ditukar dengan induknya. Setelah ditukar, heap terlihat seperti berikut ini.

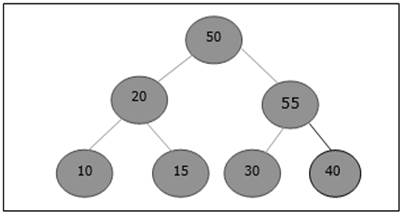
Sekali lagi, elemen tersebut melanggar properti heap. Oleh karena itu, ia ditukar dengan induknya.

Sekarang, kita harus berhenti.

Metode heapify mengatur ulang elemen array di mana sub-pohon kiri dan kanan i^th elemen mematuhi properti heap.

Algorithm: Max-Heapify(numbers[], i) 
leftchild := numbers[2i] 
rightchild := numbers [2i + 1] 
if leftchild ≤ numbers[].size and numbers[leftchild] > numbers[i] 
   largest := leftchild 
else 
   largest := i 
if rightchild ≤ numbers[].size and numbers[rightchild] > numbers[largest] 
   largest := rightchild 
if largest ≠ i 
   swap numbers[i] with numbers[largest] 
   Max-Heapify(numbers, largest)

Jika larik yang disediakan tidak mematuhi properti heap, Heap dibuat berdasarkan algoritme berikut Build-Max-Heap (numbers[]).

Algorithm: Build-Max-Heap(numbers[]) 
numbers[].size := numbers[].length 
fori = ⌊ numbers[].length/2 ⌋ to 1 by -1 
   Max-Heapify (numbers[], i)

Metode ekstrak digunakan untuk mengekstrak elemen root dari Heap. Berikut algoritmanya.

Algorithm: Heap-Extract-Max (numbers[]) 
max = numbers[1] 
numbers[1] = numbers[heapsize] 
heapsize = heapsize – 1 
Max-Heapify (numbers[], 1) 
return max

Contoh

Mari kita perhatikan contoh yang sama yang telah dibahas sebelumnya. Sekarang kami ingin mengekstrak elemen. Metode ini akan mengembalikan elemen root dari heap.

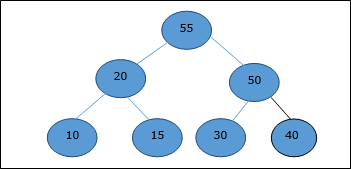
Setelah elemen root dihapus, elemen terakhir akan dipindahkan ke posisi root.

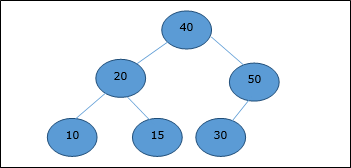
Sekarang, fungsi Heapify akan dipanggil. Setelah Heapify, heap berikut dibuat.

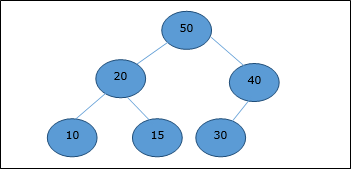
Bubble Sort adalah algoritme pengurutan dasar, yang bekerja dengan bertukar berulang kali elemen yang berdekatan, jika perlu. Ketika tidak ada pertukaran yang diperlukan, file diurutkan.

Ini adalah teknik paling sederhana di antara semua algoritma pengurutan.

Algorithm: Sequential-Bubble-Sort (A) 
fori← 1 to length [A] do 
for j ← length [A] down-to i +1 do 
   if A[A] < A[j - 1] then 
      Exchange A[j] ↔ A[j-1]

Penerapan

voidbubbleSort(int numbers[], intarray_size) { 
   inti, j, temp; 
   for (i = (array_size - 1); i >= 0; i--) 
   for (j = 1; j <= i; j++) 
      if (numbers[j - 1] > numbers[j]) { 
         temp = numbers[j-1]; 
         numbers[j - 1] = numbers[j]; 
         numbers[j] = temp; 
      } 
}

Analisis

Di sini, jumlah perbandingannya

1 + 2 + 3 +...+ (n - 1) = n(n - 1)/2 = O(n²)

Jelas, grafik menunjukkan n² sifat dari jenis gelembung.

Dalam algoritma ini, jumlah perbandingan tidak bergantung pada kumpulan datanya, yaitu apakah elemen masukan yang diberikan berada dalam urutan yang diurutkan atau dalam urutan terbalik atau secara acak.

Persyaratan Memori

Dari algoritma yang disebutkan di atas, terlihat jelas bahwa bubble sort tidak membutuhkan memori tambahan.

Contoh

Unsorted list:

5 2 1 4 3 7 6

1 ^st iterasi:

5 > 2 swap	2 5 1 4 3 7 6
5 > 1 swap	2 1 5 4 3 7 6
5 > 4 swap	2 1 4 5 3 7 6
5 > 3 swap	2 1 4 3 5 7 6
5 < 7 no swap	2 1 4 3 5 7 6
7 > 6 swap	2 1 4 3 5 6 7

2^nd iteration:

2 > 1 swap	1 2 4 3 5 6 7
2 < 4 no swap	1 2 4 3 5 6 7
4 > 3 swap	1 2 3 4 5 6 7
4 < 5 no swap	1 2 3 4 5 6 7
5 < 6 no swap	1 2 3 4 5 6 7

There is no change in 3^rd, 4^th, 5^th and 6^th iteration.

Finally,

the sorted list is

1 2 3 4 5 6 7

Insertion sort is a very simple method to sort numbers in an ascending or descending order. This method follows the incremental method. It can be compared with the technique how cards are sorted at the time of playing a game.

The numbers, which are needed to be sorted, are known as keys. Here is the algorithm of the insertion sort method.

Algorithm: Insertion-Sort(A) 
for j = 2 to A.length 
   key = A[j] 
   i = j – 1 
   while i > 0 and A[i] > key 
      A[i + 1] = A[i] 
      i = i -1 
   A[i + 1] = key

Analysis

Run time of this algorithm is very much dependent on the given input.

If the given numbers are sorted, this algorithm runs in O(n) time. If the given numbers are in reverse order, the algorithm runs in O(n²) time.

Example

Unsorted list:

2 13 5 18 14

1^st iteration:

Key = a[2] = 13

a[1] = 2 < 13

Swap, no swap

2 13 5 18 14

2^nd iteration:

Key = a[3] = 5

a[2] = 13 > 5

Swap 5 and 13

2 5 13 18 14

Next, a[1] = 2 < 13

Swap, no swap

2 5 13 18 14

3^rd iteration:

Key = a[4] = 18

a[3] = 13 < 18,

a[2] = 5 < 18,

a[1] = 2 < 18

Swap, no swap

2 5 13 18 14

4^th iteration:

Key = a[5] = 14

a[4] = 18 > 14

Swap 18 and 14

2 5 13 14 18

Next, a[3] = 13 < 14,

a[2] = 5 < 14,

a[1] = 2 < 14

So, no swap

2 5 13 14 18

Finally,

the sorted list is

2 5 13 14 18

This type of sorting is called Selection Sort as it works by repeatedly sorting elements. It works as follows: first find the smallest in the array and exchange it with the element in the first position, then find the second smallest element and exchange it with the element in the second position, and continue in this way until the entire array is sorted.

Algorithm: Selection-Sort (A) 
fori ← 1 to n-1 do 
   min j ← i; 
   min x ← A[i] 
   for j ←i + 1 to n do 
      if A[j] < min x then 
         min j ← j 
         min x ← A[j] 
   A[min j] ← A [i] 
   A[i] ← min x

Selection sort is among the simplest of sorting techniques and it works very well for small files. It has a quite important application as each item is actually moved at the most once.

Section sort is a method of choice for sorting files with very large objects (records) and small keys. The worst case occurs if the array is already sorted in a descending order and we want to sort them in an ascending order.

Nonetheless, the time required by selection sort algorithm is not very sensitive to the original order of the array to be sorted: the test if A[j] < min x is executed exactly the same number of times in every case.

Selection sort spends most of its time trying to find the minimum element in the unsorted part of the array. It clearly shows the similarity between Selection sort and Bubble sort.

• Bubble sort selects the maximum remaining elements at each stage, but wastes some effort imparting some order to an unsorted part of the array.

• Selection sort is quadratic in both the worst and the average case, and requires no extra memory.

For each i from 1 to n - 1, there is one exchange and n - i comparisons, so there is a total of n - 1 exchanges and

(n − 1) + (n − 2) + ...+ 2 + 1 = n(n − 1)/2 comparisons.

These observations hold, no matter what the input data is.

In the worst case, this could be quadratic, but in the average case, this quantity is O(n log n). It implies that the running time of Selection sort is quite insensitive to the input.

Implementation

Void Selection-Sort(int numbers[], int array_size) { 
   int i, j; 
   int min, temp;  
   for (i = 0; I < array_size-1; i++) { 
      min = i; 
      for (j = i+1; j < array_size; j++) 
         if (numbers[j] < numbers[min]) 
            min = j; 
      temp = numbers[i]; 
      numbers[i] = numbers[min]; 
      numbers[min] = temp; 
   } 
}

Example

Unsorted list:

5 2 1 4 3

1^st iteration:

Smallest = 5

2 < 5, smallest = 2

1 < 2, smallest = 1

4 > 1, smallest = 1

3 > 1, smallest = 1

Swap 5 and 1

1 2 5 4 3

2^nd iteration:

Smallest = 2

2 < 5, smallest = 2

2 < 4, smallest = 2

2 < 3, smallest = 2

No Swap

1 2 5 4 3

3^rd iteration:

Smallest = 5

4 < 5, smallest = 4

3 < 4, smallest = 3

Swap 5 and 3

1 2 3 4 5

4^th iteration:

Smallest = 4

4 < 5, smallest = 4

No Swap

1 2 3 4 5

Finally,

the sorted list is

1 2 3 4 5

It is used on the principle of divide-and-conquer. Quick sort is an algorithm of choice in many situations as it is not difficult to implement. It is a good general purpose sort and it consumes relatively fewer resources during execution.

Advantages

• It is in-place since it uses only a small auxiliary stack.

• It requires only n (log n) time to sort n items.

• It has an extremely short inner loop.

• This algorithm has been subjected to a thorough mathematical analysis, a very precise statement can be made about performance issues.

Disadvantages

• It is recursive. Especially, if recursion is not available, the implementation is extremely complicated.

• It requires quadratic (i.e., n2) time in the worst-case.

• It is fragile, i.e. a simple mistake in the implementation can go unnoticed and cause it to perform badly.

Quick sort works by partitioning a given array A[p ... r] into two non-empty sub array A[p ... q] and A[q+1 ... r] such that every key in A[p ... q] is less than or equal to every key in A[q+1 ... r].

Then, the two sub-arrays are sorted by recursive calls to Quick sort. The exact position of the partition depends on the given array and index q is computed as a part of the partitioning procedure.

Algorithm: Quick-Sort (A, p, r) 
if p < r then 
   q Partition (A, p, r) 
   Quick-Sort (A, p, q) 
   Quick-Sort (A, q + r, r)

Note that to sort the entire array, the initial call should be Quick-Sort (A, 1, length[A])

As a first step, Quick Sort chooses one of the items in the array to be sorted as pivot. Then, the array is partitioned on either side of the pivot. Elements that are less than or equal to pivot will move towards the left, while the elements that are greater than or equal to pivot will move towards the right.

Partitioning the Array

Partitioning procedure rearranges the sub-arrays in-place.

Function: Partition (A, p, r) 
x ← A[p] 
i ← p-1 
j ← r+1 
while TRUE do 
   Repeat j ← j - 1 
   until A[j] ≤ x  
   Repeat i← i+1 
   until A[i] ≥ x  
   if i < j then  
      exchange A[i] ↔ A[j] 
   else  
      return j

Analysis

The worst case complexity of Quick-Sort algorithm is O(n²). However using this technique, in average cases generally we get the output in O(n log n) time.

Radix sort is a small method that many people intuitively use when alphabetizing a large list of names. Specifically, the list of names is first sorted according to the first letter of each name, that is, the names are arranged in 26 classes.

Intuitively, one might want to sort numbers on their most significant digit. However, Radix sort works counter-intuitively by sorting on the least significant digits first. On the first pass, all the numbers are sorted on the least significant digit and combined in an array. Then on the second pass, the entire numbers are sorted again on the second least significant digits and combined in an array and so on.

Algorithm: Radix-Sort (list, n) 
shift = 1 
for loop = 1 to keysize do 
   for entry = 1 to n do 
      bucketnumber = (list[entry].key / shift) mod 10 
      append (bucket[bucketnumber], list[entry]) 
   list = combinebuckets() 
   shift = shift * 10

Analisis

Setiap kunci dilihat sekaligus untuk setiap digit (atau huruf jika kuncinya alfabet) dari kunci terpanjang. Oleh karena itu, jika kunci terpanjang memilikim digit dan ada n kunci, jenis radix memiliki urutan O(m.n).

Namun, jika kita melihat kedua nilai tersebut, ukuran kunci akan relatif kecil jika dibandingkan dengan jumlah kunci. Misalnya, jika kita memiliki kunci enam digit, kita dapat memiliki jutaan rekaman berbeda.

Di sini, kami melihat bahwa ukuran kunci tidak signifikan, dan algoritme ini memiliki kompleksitas linier O(n).

Contoh

Contoh berikut menunjukkan bagaimana Radix sort beroperasi pada tujuh angka 3-digit.

Memasukkan	1 st Lulus	2 nd Lulus	3 rd Lulus
329	720	720	329
457	355	329	355
657	436	436	436
839	457	839	457
436	657	355	657
720	329	457	720
355	839	657	839

Dalam contoh di atas, kolom pertama adalah input. Kolom yang tersisa menampilkan daftar setelah pengurutan berturut-turut pada posisi digit yang semakin signifikan. Kode untuk Radix sort mengasumsikan bahwa setiap elemen dalam sebuah arrayA dari n elemen memiliki d digit, dimana digit 1 adalah digit urutan terendah dan d adalah digit urutan tertinggi.

Untuk memahami kelas P dan NP, pertama-tama kita harus mengetahui model komputasi. Karenanya, dalam bab ini kita akan membahas dua model komputasi penting.

Perhitungan Determinan dan Kelas P

Mesin Turing Determinan

Salah satu model ini adalah mesin Turing satu pita deterministik. Mesin ini terdiri dari kontrol keadaan hingga, kepala baca-tulis, dan pita dua arah dengan urutan tak terbatas.

Berikut adalah diagram skema dari mesin Turing satu pita deterministik.

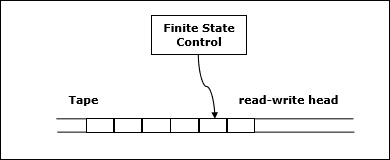
Sebuah program untuk mesin Turing deterministik menetapkan informasi berikut -

• Satu set simbol pita terbatas (simbol input dan simbol kosong)
• Sekumpulan negara yang terbatas
• Fungsi transisi

Dalam analisis algoritmik, jika suatu masalah dapat dipecahkan dalam waktu polinomial oleh mesin Turing satu pita deterministik, masalah tersebut termasuk dalam kelas P.

Perhitungan Nondeterministik dan Kelas NP

Mesin Turing Nondeterministic

Untuk mengatasi masalah komputasi, model lain adalah Non-deterministic Turing Machine (NDTM). Struktur NDTM mirip dengan DTM, namun di sini kami memiliki satu modul tambahan yang disebut modul menebak, yang dikaitkan dengan satu kepala tulis saja.

Berikut diagram skematiknya.

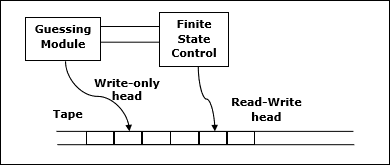
Jika masalah dapat diselesaikan dalam waktu polinomial oleh mesin Turing non-deterministik, masalah tersebut termasuk dalam kelas NP.

Dalam grafik tidak berarah, a cliqueadalah sub-grafik lengkap dari grafik yang diberikan. Sub-grafik lengkap berarti, semua simpul dari sub-grafik ini terhubung ke semua simpul lain dari sub-grafik ini.

Masalah Max-Clique adalah masalah komputasi untuk menemukan klik maksimum dari grafik. Klik maks digunakan dalam banyak masalah dunia nyata.

Mari kita pertimbangkan aplikasi jejaring sosial, di mana simpul mewakili profil orang dan tepi mewakili kenalan bersama dalam grafik. Dalam grafik ini, klik mewakili subkumpulan orang yang semuanya saling mengenal.

Untuk menemukan klik maksimum, seseorang dapat secara sistematis memeriksa semua himpunan bagian, tetapi jenis pencarian brute force ini terlalu memakan waktu untuk jaringan yang terdiri lebih dari beberapa lusin simpul.

Algorithm: Max-Clique (G, n, k) 
S := Φ 
for i = 1 to k do 
   t := choice (1…n)  
   if t Є S then 
      return failure 
   S := S ∪ t  
for all pairs (i, j) such that i Є S and j Є S and i ≠ j do 
   if (i, j) is not a edge of the graph then  
      return failure 
return success

Analisis

Masalah Max-Clique adalah algoritma non-deterministik. Dalam algoritma ini, pertama-tama kami mencoba menentukan satu setk simpul berbeda dan kemudian kami mencoba untuk menguji apakah simpul ini membentuk grafik lengkap.

Tidak ada algoritma deterministik waktu polinomial untuk menyelesaikan masalah ini. Masalah ini NP-Complete.

Contoh

Perhatikan grafik berikut. Di sini, sub-grafik yang berisi simpul 2, 3, 4 dan 6 membentuk grafik yang lengkap. Oleh karena itu, sub-grafik ini adalah aclique. Karena ini adalah sub-grafik lengkap maksimum dari grafik yang disediakan, ini adalah a4-Clique.

Penutup simpul dari grafik yang tidak berarah G = (V, E) adalah bagian dari simpul V^' ⊆ V sehingga jika tepi (u, v) adalah tepi G, lalu salah satunya u di V atau v di V^' atau keduanya.

Temukan penutup-puncak dengan ukuran maksimum dalam grafik yang tidak berarah. Vertexcover yang optimal ini adalah versi pengoptimalan dari masalah NP-complete. Namun demikian, tidak terlalu sulit untuk menemukan penutup-simpul yang mendekati optimal.

APPROX-VERTEX_COVER (G: Graph) c ← { } E' ← E[G] 
while E' is not empty do 
   Let (u, v) be an arbitrary edge of E' c ← c U {u, v} 
   Remove from E' every edge incident on either u or v 
return c

Contoh

Himpunan tepi dari grafik yang diberikan adalah -

{(1,6),(1,2),(1,4),(2,3),(2,4),(6,7),(4,7),(7,8),(3,8),(3,5),(8,5)}

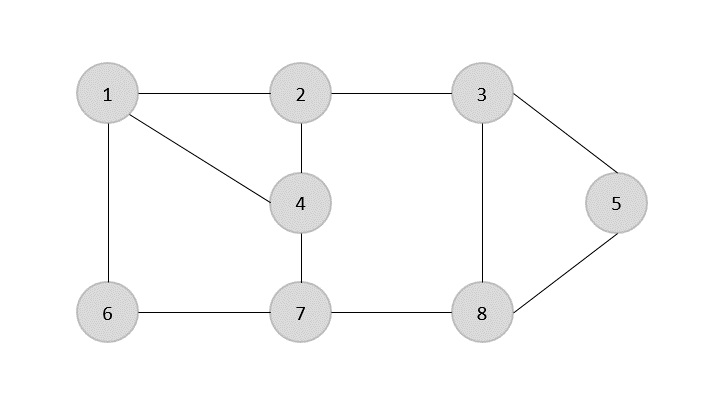
Sekarang, kita mulai dengan memilih tepi arbitrer (1,6). Kami menghilangkan semua tepi, yang bersisian dengan simpul 1 atau 6 dan kami menambahkan tepi (1,6) untuk menutupi.

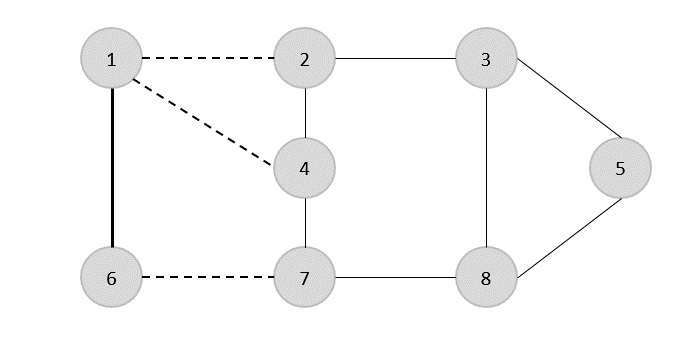
Pada langkah berikutnya, kami telah memilih sisi lain (2,3) secara acak

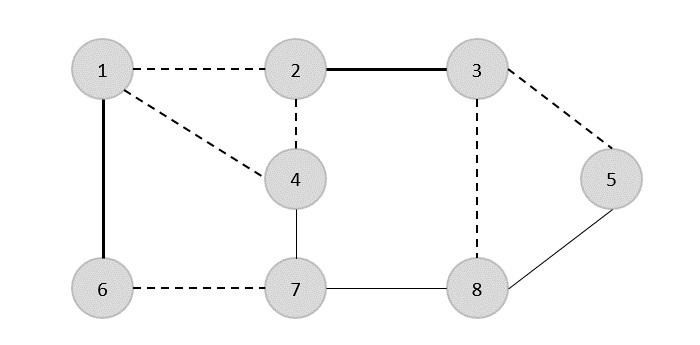
Sekarang kami memilih tepi lain (4,7).

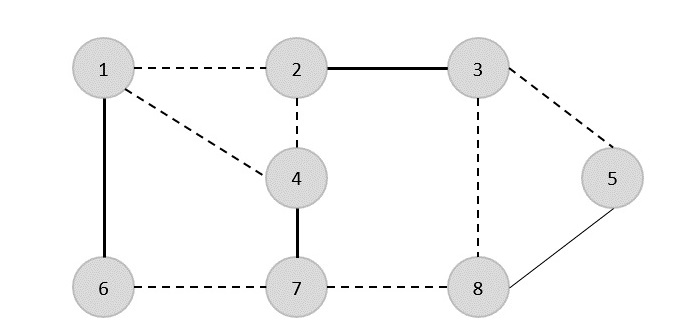
Kami memilih tepi lain (8,5).

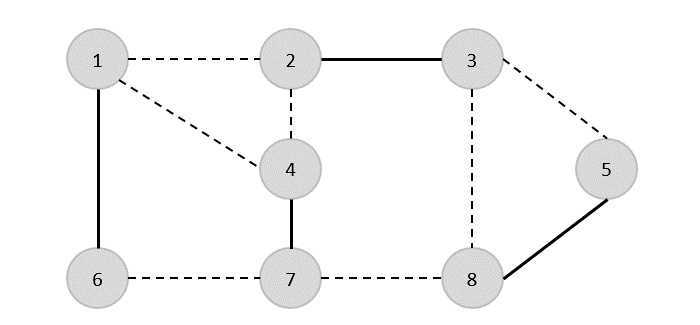
Oleh karena itu, tutup puncak grafik ini adalah {1,2,4,5}.

Analisis

Sangat mudah untuk melihat bahwa waktu berjalan dari algoritma ini adalah O(V + E), menggunakan daftar kedekatan untuk mewakili E^'.

Dalam Ilmu Komputer, banyak masalah yang diselesaikan yang tujuannya untuk memaksimalkan atau meminimalkan beberapa nilai, sedangkan di masalah lain kami mencoba mencari solusi atau tidak. Oleh karena itu, masalah dapat dikategorikan sebagai berikut -

Masalah pengoptimalan

Masalah pengoptimalan adalah masalah yang tujuannya adalah untuk memaksimalkan atau meminimalkan beberapa nilai. Sebagai contoh,

• Menemukan jumlah warna minimum yang diperlukan untuk mewarnai grafik tertentu.

• Menemukan jalur terpendek antara dua simpul dalam sebuah grafik.

Masalah Keputusan

Ada banyak masalah yang jawabannya adalah Ya atau Tidak. Jenis masalah ini dikenal sebagai decision problems. Sebagai contoh,

• Apakah grafik tertentu dapat diwarnai hanya dengan 4 warna.

• Menemukan siklus Hamiltonian dalam grafik bukanlah masalah keputusan, sedangkan memeriksa grafik adalah Hamiltonian atau bukan merupakan masalah keputusan.

Apa itu Bahasa?

Setiap masalah keputusan hanya dapat memiliki dua jawaban, ya atau tidak. Oleh karena itu, masalah keputusan mungkin menjadi milik suatu bahasa jika memberikan jawaban 'ya' untuk input tertentu. Bahasa adalah totalitas input yang jawabannya adalah Ya. Sebagian besar algoritme yang dibahas di bab sebelumnya adalahpolynomial time algorithms.

Untuk ukuran masukan n, jika kompleksitas waktu kasus terburuk dari suatu algoritme adalah O(n^k), dimana k adalah konstanta, algoritme adalah algoritme waktu polinomial.

Algoritme seperti Perkalian Rantai Matriks, Jalur Terpendek Sumber Tunggal, Jalur Terpendek Semua Pasangan, Pohon Rentang Minimum, dll. Berjalan dalam waktu polinomial. Namun ada banyak masalah, seperti penjual keliling, pewarnaan grafik yang optimal, siklus Hamiltonian, menemukan jalur terpanjang dalam grafik, dan memenuhi rumus Boolean, yang tidak diketahui algoritma waktu polinomialnya. Masalah-masalah ini termasuk dalam kelas masalah yang menarik, yang disebutNP-Complete masalah, yang statusnya tidak diketahui.

Dalam konteks ini, kita dapat mengkategorikan masalah sebagai berikut -

Kelas-P

Kelas P terdiri dari masalah-masalah yang dapat diselesaikan dalam waktu polinomial, yaitu masalah-masalah ini dapat diselesaikan dalam waktu O(n^k) dalam kasus terburuk, di mana k konstan.

Masalah ini disebut tractable, sementara yang lain dipanggil intractable or superpolynomial.

Secara formal, algoritme adalah algoritme waktu polinomial, jika terdapat polinomial p(n) sedemikian rupa sehingga algoritme dapat menyelesaikan contoh ukuran apa pun n pada suatu waktu O(p(n)).

Masalah yang membutuhkan Ω(n⁵⁰) waktu untuk menyelesaikan pada dasarnya sulit untuk besar n. Algoritme waktu polinomial yang paling dikenal berjalan dalam waktuO(n^k) untuk nilai yang cukup rendah k.

Keuntungan dalam mempertimbangkan kelas algoritma waktu polinomial adalah semua itu masuk akal deterministic single processor model of computation dapat disimulasikan satu sama lain dengan paling banyak lambat polinomial-d

NP-Class

NP kelas terdiri dari masalah-masalah yang dapat diverifikasi dalam waktu polinomial. NP adalah kelas masalah keputusan yang mudah untuk memeriksa kebenaran jawaban yang diklaim, dengan bantuan sedikit informasi tambahan. Oleh karena itu, kami tidak meminta cara untuk menemukan solusi, tetapi hanya untuk memverifikasi bahwa solusi yang dituduhkan benar-benar tepat.

Setiap masalah di kelas ini dapat diselesaikan dalam waktu eksponensial menggunakan pencarian lengkap.

P versus NP

Setiap masalah keputusan yang dapat diselesaikan dengan algoritma waktu polinomial deterministik juga dapat diselesaikan dengan algoritma non-deterministik waktu polinomial.

Semua masalah di P dapat diselesaikan dengan algoritma waktu polinomial, sedangkan semua masalah di NP - P tidak bisa dipecahkan .

Tidak diketahui apakah P = NP. Namun, banyak masalah yang diketahui dalam NP dengan sifat bahwa jika termasuk dalam P, maka dapat dibuktikan bahwa P = NP.

Jika P ≠ NP, ada masalah di NP yang bukan di P maupun di NP-Complete.

Masalahnya milik kelas Pjika mudah menemukan solusi untuk masalah tersebut. Masalahnya milikNP, jika mudah untuk memeriksa solusi yang mungkin sangat membosankan untuk ditemukan.

Stephen Cook mempresentasikan empat teorema dalam makalahnya “Prosedur Pembuktian Teorema Kompleksitas”. Teorema ini dinyatakan di bawah ini. Kami memahami bahwa banyak istilah yang tidak diketahui digunakan dalam bab ini, tetapi kami tidak memiliki ruang lingkup untuk membahas semuanya secara rinci.

Berikut adalah empat teorema oleh Stephen Cook -

Teorema-1

Jika satu set S string diterima oleh beberapa mesin Turing non-deterministik dalam waktu polinomial, lalu S adalah P-reducible menjadi {DNF tautologies}.

Teorema-2

Kumpulan berikut dapat direduksi-P satu sama lain secara berpasangan (dan karenanya masing-masing memiliki tingkat kesulitan polinomial yang sama): {tautologies}, {DNF tautologies}, D3, {sub-graph pairs}.

Teorema-3

• Untuk apapun T_Q(k) dari tipe Q, $\mathbf{\frac{T_{Q}(k)}{\frac{\sqrt{k}}{(log\:k)^2}}}$ tidak terbatas

• Ada sebuah T_Q(k) dari tipe Q seperti yang $T_{Q}(k)\leqslant 2^{k(log\:k)^2}$

Teorema-4

Jika set string S diterima oleh mesin non-deterministik dalam waktu T(n) = 2ⁿ, dan jika T_Q(k) adalah fungsi tipe yang jujur ​​(dapat dihitung secara real-time) Q, lalu ada konstanta K, jadi S dapat dikenali oleh mesin deterministik dalam waktu T_Q(K8ⁿ).

• Pertama, ia menekankan pentingnya reduksi waktu polinomial. Ini berarti bahwa jika kita memiliki pengurangan waktu polinomial dari satu masalah ke masalah lainnya, ini memastikan bahwa algoritma waktu polinomial dari masalah kedua dapat diubah menjadi algoritma waktu polinomial yang sesuai untuk masalah pertama.

• Kedua, ia memusatkan perhatian pada kelas NP dari masalah keputusan yang dapat diselesaikan dalam waktu polinomial oleh komputer non-deterministik. Sebagian besar masalah yang sulit diselesaikan milik kelas ini, NP.

• Ketiga, ia membuktikan bahwa satu masalah tertentu di NP memiliki properti bahwa setiap masalah lain di NP dapat direduksi secara polinomial menjadi masalah tersebut. Jika masalah kepuasan dapat diselesaikan dengan algoritma waktu polinom, maka setiap masalah dalam NP juga dapat diselesaikan dalam waktu polinomial. Jika ada masalah di NP yang sulit dipecahkan, maka masalah kepuasan harus sulit diselesaikan. Jadi, masalah kepuasan adalah masalah tersulit di NP.

• Keempat, Cook menyarankan bahwa masalah lain di NP mungkin berbagi dengan masalah kepuasan properti ini sebagai anggota NP yang paling sulit.

Masalah ada di NPC kelas jika di NP dan sebagai hardsebagai masalah di NP. Masalahnya adalahNP-hard jika semua masalah di NP adalah polynomial time yang dapat direduksi menjadi itu, meskipun mungkin tidak ada di NP itu sendiri.

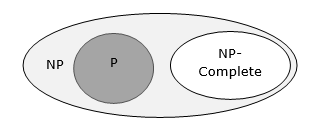
Jika algoritme waktu polinomial ada untuk salah satu masalah ini, semua masalah di NP akan dapat dipecahkan dengan waktu polinomial. Masalah ini disebutNP-complete. Fenomena kelengkapan NP penting baik untuk alasan teoritis maupun praktis.

Definisi NP-Kelengkapan

Sebuah bahasa B adalah NP-complete jika memenuhi dua kondisi

• B ada di NP

• Setiap A di NP adalah waktu polinomial yang dapat direduksi menjadi B.

Jika suatu bahasa memenuhi properti kedua, tetapi belum tentu yang pertama, bahasa B diketahui sebagai NP-Hard. Secara informal, masalah pencarianB adalah NP-Hard jika ada beberapa NP-Complete masalah A yang direduksi Turing menjadi B.

Masalah di NP-Hard tidak dapat diselesaikan dalam waktu polinomial, sampai P = NP. Jika suatu masalah terbukti sebagai NPC, tidak perlu membuang waktu untuk mencoba menemukan algoritma yang efisien untuk itu. Sebagai gantinya, kita dapat fokus pada algoritma pendekatan desain.

Masalah NP-Complete

Berikut adalah beberapa masalah NP-Complete, yang tidak diketahui algoritma waktu polinomialnya.

• Menentukan apakah graf memiliki siklus Hamiltonian
• Menentukan apakah rumus Boolean memuaskan, dll.

Masalah NP-Hard

Masalah berikut adalah NP-Hard

• Masalah kepuasan sirkuit
• Set Cover
• Penutup Vertex
• Masalah Penjual Bepergian

Dalam konteks ini, sekarang kita akan membahas TSP yaitu NP-Complete

TSP adalah NP-Complete

Masalah salesman keliling terdiri dari seorang salesman dan sekumpulan kota. Penjual harus mengunjungi setiap kota mulai dari kota tertentu dan kembali ke kota yang sama. Tantangan dari masalah ini adalah penjual keliling ingin meminimalkan total lama perjalanan

Bukti

Untuk membuktikan TSP is NP-Complete, pertama kita harus membuktikannya TSP belongs to NP. Di TSP, kami menemukan tur dan memeriksa bahwa tur tersebut berisi setiap simpul satu kali. Kemudian total biaya tepi tur dihitung. Akhirnya, kami memeriksa apakah biayanya minimum. Ini dapat diselesaikan dalam waktu polinomial. JadiTSP belongs to NP.

Kedua, kita harus membuktikannya TSP is NP-hard. Untuk membuktikannya, salah satu caranya adalah dengan menunjukkannyaHamiltonian cycle ≤_p TSP (seperti yang kita ketahui bahwa masalah siklus Hamiltonian adalah NPcomplete).

Menganggap G = (V, E) menjadi contoh siklus Hamiltonian.

Oleh karena itu, turunan TSP dibangun. Kami membuat grafik lengkapG^' = (V, E^'), dimana

$$E^{'}=\lbrace(i, j)\colon i, j \in V \:\:and\:i\neq j$$

Jadi, fungsi biaya didefinisikan sebagai berikut -

$$t(i,j)=\begin{cases}0 & if\: (i, j)\: \in E\\1 & otherwise\end{cases}$$

Sekarang, anggaplah itu siklus Hamiltonian h ada di G. Jelas bahwa biaya setiap sisi masukh adalah 0 di G^' karena setiap sisi milik E. Karena itu,h memiliki biaya sebesar 0 di G^'. Jadi, jika grafikG memiliki siklus Hamiltonian, lalu grafik G^' memiliki tur 0 biaya.

Sebaliknya, kami berasumsi demikian G^' mengadakan tur h^' biaya paling banyak 0. Biaya tepi masukE^' adalah 0 dan 1Menurut definisi. Oleh karena itu, setiap sisi harus memiliki biaya sebesar0 sebagai biaya h^' adalah 0. Oleh karena itu kami menyimpulkan ituh^' hanya berisi tepi dalam E.

Dengan demikian, kami telah membuktikannya G memiliki siklus Hamiltonian, jika dan hanya jika G^' memiliki tur dengan biaya paling banyak 0. TSP adalah NP-complete.

Algoritma yang dibahas pada bab-bab sebelumnya berjalan secara sistematis. Untuk mencapai tujuan, satu atau lebih jalur yang dieksplorasi sebelumnya menuju solusi perlu disimpan untuk menemukan solusi optimal.

Untuk banyak masalah, jalan menuju tujuan tidak relevan. Misalnya, dalam masalah N-Queens, kita tidak perlu peduli tentang konfigurasi akhir dari ratu serta urutan penambahan ratu.

Mendaki Bukit

Hill Climbing adalah teknik untuk memecahkan masalah pengoptimalan tertentu. Dalam teknik ini, kita mulai dengan solusi sub-optimal dan solusi tersebut diperbaiki berulang kali hingga beberapa kondisi dimaksimalkan.

Ide memulai dengan solusi sub-optimal dibandingkan dengan memulai dari dasar bukit, memperbaiki solusi dibandingkan dengan berjalan di atas bukit, dan terakhir memaksimalkan beberapa kondisi dibandingkan mencapai puncak bukit.

Oleh karena itu, teknik mendaki bukit dapat dianggap sebagai tahapan berikut -

• Membangun solusi sub-optimal dengan mematuhi kendala masalah
• Memperbaiki solusi langkah demi langkah
• Memperbaiki solusi sampai tidak ada lagi perbaikan yang mungkin dilakukan

Teknik Hill Climbing terutama digunakan untuk memecahkan masalah komputasi yang sulit. Ini hanya terlihat pada keadaan saat ini dan keadaan segera di masa depan. Oleh karena itu, teknik ini hemat memori karena tidak mempertahankan pohon pencarian.

Algorithm: Hill Climbing 
Evaluate the initial state. 
Loop until a solution is found or there are no new operators left to be applied: 
   - Select and apply a new operator 
   - Evaluate the new state: 
      goal -→ quit 
      better than current state -→ new current state

Peningkatan Iteratif

Dalam metode perbaikan berulang, solusi optimal dicapai dengan membuat kemajuan menuju solusi optimal di setiap iterasi. Namun, teknik ini mungkin menemui maksima lokal. Dalam situasi ini, tidak ada negara terdekat untuk solusi yang lebih baik.

Masalah ini dapat dihindari dengan berbagai metode. Salah satu metode ini adalah simulasi anil.

Mulai Ulang Acak

Ini adalah metode lain untuk memecahkan masalah optima lokal. Teknik ini melakukan serangkaian pencarian. Setiap kali, ini dimulai dari keadaan awal yang dibuat secara acak. Oleh karena itu, solusi optima atau hampir optimal dapat diperoleh dengan membandingkan solusi pencarian yang dilakukan.

Permasalahan Teknik Mendaki Bukit

Maxima Lokal

Jika heuristik tidak cembung, Hill Climbing dapat menyatu dengan maksimum lokal, bukan maksimum global.

Ridges dan Alleys

Jika fungsi target membuat punggungan sempit, maka pemanjat hanya bisa naik punggungan atau menuruni gang dengan cara zig-zag. Dalam skenario ini, pemanjat perlu mengambil langkah-langkah yang sangat kecil yang membutuhkan lebih banyak waktu untuk mencapai tujuan.

Dataran

Dataran tinggi ditemui saat ruang pencarian datar atau cukup datar sehingga nilai yang dikembalikan oleh fungsi target tidak dapat dibedakan dari nilai yang dikembalikan untuk wilayah terdekat, karena presisi yang digunakan mesin untuk mewakili nilainya.

Kompleksitas Teknik Mendaki Bukit

Teknik ini tidak mengalami masalah yang berhubungan dengan ruang, karena hanya melihat keadaan saat ini. Jalur yang dijelajahi sebelumnya tidak disimpan.

Untuk sebagian besar masalah dalam teknik Random-restart Hill Climbing, solusi optimal dapat dicapai dalam waktu polinomial. Namun, untuk masalah NP-Complete, waktu komputasi dapat menjadi eksponensial berdasarkan jumlah maksima lokal.

Aplikasi Teknik Hill Climbing

Teknik Hill Climbing dapat digunakan untuk memecahkan banyak masalah, dimana keadaan saat ini memungkinkan untuk fungsi evaluasi yang akurat, seperti Aliran Jaringan, masalah Penjual Perjalanan, masalah 8-Ratu, desain Sirkuit Terpadu, dll.

Hill Climbing juga digunakan dalam metode pembelajaran induktif. Teknik ini digunakan dalam robotika untuk koordinasi di antara beberapa robot dalam satu tim. Ada banyak masalah lain di mana teknik ini digunakan.

Contoh

Teknik ini dapat diterapkan untuk mengatasi masalah travelling salesman. Pertama, solusi awal ditentukan bahwa mengunjungi semua kota tepat satu kali. Oleh karena itu, solusi awal ini tidak optimal dalam banyak kasus. Bahkan solusi ini bisa sangat buruk. Algoritme Hill Climbing dimulai dengan solusi awal seperti itu dan memperbaikinya secara berulang. Akhirnya, rute yang jauh lebih pendek kemungkinan akan diperoleh.