DAA - Pohon Pencarian Biner Biaya Optimal

Binary Search Tree (BST) adalah pohon tempat nilai-nilai kunci disimpan di node internal. Node eksternal adalah node nol. Kunci diurutkan secara leksikografis, yaitu untuk setiap node internal semua kunci di sub-pohon kiri lebih kecil dari kunci di node, dan semua kunci di sub-pohon kanan lebih besar.

Ketika kita mengetahui frekuensi pencarian setiap kunci, cukup mudah untuk menghitung biaya yang diharapkan untuk mengakses setiap node di pohon. Pohon pencarian biner yang optimal adalah BST, yang memiliki biaya minimal yang diharapkan untuk menemukan setiap node

Waktu pencarian elemen dalam BST adalah O(n), sedangkan dalam waktu pencarian Balanced-BST adalah O(log n). Sekali lagi waktu pencarian dapat ditingkatkan dalam Pohon Pencarian Biner Biaya Optimal, menempatkan data yang paling sering digunakan di root dan lebih dekat ke elemen root, sambil menempatkan data yang paling jarang digunakan di dekat daun dan daun.

Di sini, Algoritma Pohon Pencarian Biner Optimal disajikan. Pertama, kami membangun BST dari kumpulan yang disediakann jumlah kunci yang berbeda < k₁, k₂, k₃, ... k_n >. Di sini kami berasumsi, kemungkinan mengakses kunciK_i adalah p_i. Beberapa kunci boneka (d₀, d₁, d₂, ... d_n) ditambahkan karena beberapa pencarian dapat dilakukan untuk nilai-nilai yang tidak ada dalam kumpulan Kunci K. Kami berasumsi, untuk setiap kunci dummyd_i kemungkinan akses adalah q_i.

Optimal-Binary-Search-Tree(p, q, n) 
e[1…n + 1, 0…n],  
w[1…n + 1, 0…n], 
root[1…n + 1, 0…n]  
for i = 1 to n + 1 do 
   e[i, i - 1] := qi - 1 
   w[i, i - 1] := qi - 1  
for l = 1 to n do 
   for i = 1 to n – l + 1 do 
      j = i + l – 1 e[i, j] := ∞ 
      w[i, i] := w[i, i -1] + pj + qj 
      for r = i to j do 
         t := e[i, r - 1] + e[r + 1, j] + w[i, j] 
         if t < e[i, j] 
            e[i, j] := t 
            root[i, j] := r 
return e and root

Analisis

Algoritme membutuhkan O (n³) waktu, sejak tiga bersarang forloop digunakan. Masing-masing loop ini mengambil paling banyakn nilai-nilai.

Contoh

Mempertimbangkan pohon berikut, biayanya 2,80, meskipun ini bukan hasil yang optimal.

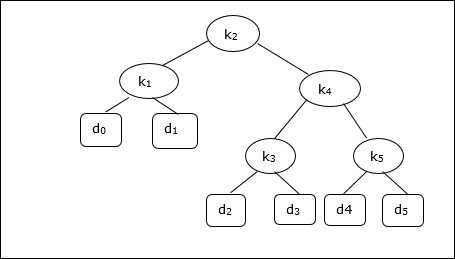
Node	Kedalaman	Kemungkinan	Kontribusi
k 1	1	0.15	0.30
k 2	0	0.10	0.10
k 3	2	0,05	0.15
k 4	1	0.10	0.20
k 5	2	0.20	0.60
d 0	2	0,05	0.15
d 1	2	0.10	0.30
d 2	3	0,05	0.20
d 3	3	0,05	0.20
d 4	3	0,05	0.20
d 5	3	0.10	0.40
Total			2.80

Untuk mendapatkan solusi yang optimal, dengan menggunakan algoritma yang dibahas dalam bab ini, tabel berikut dibuat.

Dalam tabel berikut, indeks kolom adalah i dan indeks baris adalah j.

e	1	2	3	4	5	6
5	2.75	2.00	1.30	0.90	0,50	0.10
4	1.75	1.20	0.60	0.30	0,05
3	1.25	0.70	0.25	0,05
2	0.90	0.40	0,05
1	0.45	0.10
0	0,05

w	1	2	3	4	5	6
5	1.00	0.80	0.60	0,50	0.35	0.10
4	0.70	0,50	0.30	0.20	0,05
3	0,55	0.35	0.15	0,05
2	0.45	0.25	0,05
1	0.30	0.10
0	0,05

akar	1	2	3	4	5
5	2	4	5	5	5
4	2	2	4	4
3	2	2	3
2	1	2
1	1

Dari tabel-tabel ini, pohon yang optimal dapat dibentuk.