Modellazione di sistemi meccanici
In questo capitolo, discutiamo di differential equation modelingdi sistemi meccanici. Esistono due tipi di sistemi meccanici in base al tipo di movimento.
- Sistemi meccanici traslazionali
- Sistemi meccanici rotazionali
Modellazione di sistemi meccanici traslazionali
I sistemi meccanici traslazionali si muovono lungo a straight line. Questi sistemi consistono principalmente di tre elementi di base. Quelli sono massa, molla e dashpot o ammortizzatore.
Se una forza viene applicata a un sistema meccanico traslazionale, allora viene contrastata da forze opposte dovute alla massa, all'elasticità e all'attrito del sistema. Poiché la forza applicata e le forze opposte sono in direzioni opposte, la somma algebrica delle forze che agiscono sul sistema è zero. Vediamo ora la forza contrastata da questi tre elementi individualmente.
Massa
La massa è proprietà di un corpo, che immagazzina kinetic energy. Se viene applicata una forza su un corpo avente massaM, allora si oppone a una forza opposta dovuta alla massa. Questa forza opposta è proporzionale all'accelerazione del corpo. Supponiamo che elasticità e attrito siano trascurabili.

$$ F_m \ propto \: a $$
$$ \ Rightarrow F_m = Ma = M \ frac {\ text {d} ^ 2x} {\ text {d} t ^ 2} $$
$$ F = F_m = M \ frac {\ text {d} ^ 2x} {\ text {d} t ^ 2} $$
Dove,
F è la forza applicata
Fm è la forza opposta dovuta alla massa
M è massa
a è l'accelerazione
x è lo spostamento
Primavera
La primavera è un elemento che immagazzina potential energy. Se viene applicata una forza sulla mollaK, allora è contrastata da una forza contraria dovuta all'elasticità della molla. Questa forza opposta è proporzionale allo spostamento della molla. Supponiamo che la massa e l'attrito siano trascurabili.

$$ F \ propto \: x $$
$$ \ Rightarrow F_k = Kx $$
$$ F = F_k = Kx $$
Dove,
F è la forza applicata
Fk è la forza contraria dovuta all'elasticità della molla
K è la costante della primavera
x è lo spostamento
Dashpot
Se viene applicata una forza sul dashpot B, allora si oppone a una forza opposta a causa di frictiondel dashpot. Questa forza opposta è proporzionale alla velocità del corpo. Supponiamo che massa ed elasticità siano trascurabili.

$$ F_b \ propto \: \ nu $$
$$ \ Rightarrow F_b = B \ nu = B \ frac {\ text {d} x} {\ text {d} t} $$
$$ F = F_b = B \ frac {\ text {d} x} {\ text {d} t} $$
Dove,
Fb è la forza opposta dovuta all'attrito del dashpot
B è il coefficiente di attrito
v è la velocità
x è lo spostamento
Modellazione di sistemi meccanici rotazionali
I sistemi meccanici rotazionali si muovono su un asse fisso. Questi sistemi consistono principalmente di tre elementi di base. Quelli sonomoment of inertia, torsional spring e dashpot.
Se una coppia viene applicata a un sistema meccanico rotazionale, allora viene contrastata da coppie opposte dovute al momento di inerzia, elasticità e attrito del sistema. Poiché la coppia applicata e le coppie opposte sono in direzioni opposte, la somma algebrica delle coppie agenti sul sistema è zero. Vediamo ora la coppia opposta da questi tre elementi singolarmente.
Momento d'inerzia
Nel sistema meccanico traslazionale, la massa immagazzina l'energia cinetica. Allo stesso modo, nel sistema meccanico rotazionale, il momento di inerzia memorizzakinetic energy.
Se viene applicata una coppia su un corpo con momento di inerzia J, allora viene contrastata da una coppia contraria dovuta al momento d'inerzia. Questa coppia opposta è proporzionale all'accelerazione angolare del corpo. Supponiamo che elasticità e attrito siano trascurabili.

$$ T_j \ propto \: \ alpha $$
$$ \ Rightarrow T_j = J \ alpha = J \ frac {\ text {d} ^ 2 \ theta} {\ text {d} t ^ 2} $$
$$ T = T_j = J \ frac {\ text {d} ^ 2 \ theta} {\ text {d} t ^ 2} $$
Dove,
T è la coppia applicata
Tj è la coppia contraria dovuta al momento d'inerzia
J è il momento di inerzia
α è l'accelerazione angolare
θ è lo spostamento angolare
Molla torsionale
Nel sistema meccanico traslazionale, la molla immagazzina energia potenziale. Allo stesso modo, nel sistema meccanico rotazionale, molle torsionalipotential energy.
Se viene applicata una coppia alla molla di torsione K, allora è contrastata da una coppia opposta dovuta all'elasticità della molla di torsione. Questa coppia opposta è proporzionale allo spostamento angolare della molla di torsione. Supponiamo che il momento di inerzia e di attrito siano trascurabili.
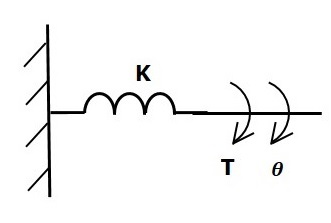
$$ T_k \ propto \: \ theta $$
$$ \ Rightarrow T_k = K \ theta $$
$$ T = T_k = K \ theta $$
Dove,
T è la coppia applicata
Tk è la coppia opposta dovuta all'elasticità della molla di torsione
K è la costante della molla torsionale
θ è lo spostamento angolare
Dashpot
Se viene applicata una coppia sul cruscotto B, allora è contrastata da una coppia contraria dovuta al rotational frictiondel dashpot. Questa coppia opposta è proporzionale alla velocità angolare del corpo. Supponiamo che il momento di inerzia e l'elasticità siano trascurabili.
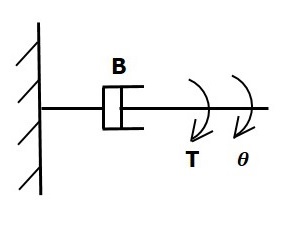
$$ T_b \ propto \: \ omega $$
$$ \ Rightarrow T_b = B \ omega = B \ frac {\ text {d} \ theta} {\ text {d} t} $$
$$ T = T_b = B \ frac {\ text {d} \ theta} {\ text {d} t} $$
Dove,
Tb è la coppia opposta dovuta all'attrito rotazionale del dashpot
B è il coefficiente di attrito rotazionale
ω è la velocità angolare
θ è lo spostamento angolare