Figure di Lissajous
Lissajous figureè il modello che viene visualizzato sullo schermo, quando i segnali sinusoidali vengono applicati alle piastre di deflessione orizzontali e verticali del CRO. Questi modelli varieranno in base alle ampiezze, frequenze e differenze di fase dei segnali sinusoidali, che vengono applicati alle piastre di deflessione sia orizzontale che verticale del CRO.
La figura seguente mostra un file example della figura di Lissajous.
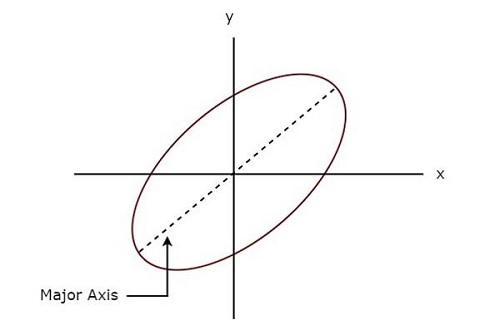
La figura di Lissajous sopra è in elliptical shape e il suo asse maggiore ha un angolo di inclinazione con asse x positivo.
Misurazioni utilizzando le figure di Lissajous
Possiamo fare quanto segue two measurements da una figura di Lissajous.
- Frequenza del segnale sinusoidale
- Differenza di fase tra due segnali sinusoidali
Ora, discutiamo di queste due misurazioni una per una.
Misurazione della frequenza
La figura di Lissajous verrà visualizzata sullo schermo, quando i segnali sinusoidali vengono applicati alle piastre di deflessione orizzontali e verticali del CRO. Quindi, applica il segnale sinusoidale, che ha standardknown frequencyalle piastre di deflessione orizzontali di CRO. Allo stesso modo, applicare il segnale sinusoidale, il cuifrequency è unknown alle piastre di deflessione verticali di CRO
Siano, $ f_ {H} $ e $ f_ {V} $ sono le frequenze dei segnali sinusoidali, che sono applicati rispettivamente alle piastre di deflessione orizzontale e verticale di CRO. La relazione tra $ f_ {H} $ e $ f_ {V} $ può esseremathematically rappresentato come di seguito.
$$ \ frac {f_ {V}} {f_ {H}} = \ frac {n_ {H}} {n_ {V}} $$
Dalla relazione sopra, otterremo la frequenza del segnale sinusoidale, che viene applicato alle piastre di deflessione verticale di CRO come
$ f_ {V} = \ left (\ frac {n_ {H}} {n_ {V}} \ right) f_ {H} $ (Equazione 1)
Dove,
$ n_ {H} $ è il numero di tangenze orizzontali
$ n_ {V} $ è il numero di tangenze verticali
Possiamo trovare i valori di $ n_ {H} $ e $ n_ {V} $ dalla figura di Lissajous. Quindi, sostituendo i valori di $ n_ {H} $, $ n_ {V} $ e $ f_ {H} $ nell'equazione 1, otterremo il valore di$f_{V}$, cioè il frequency of sinusoidal signal che viene applicato alle piastre di deflessione verticali di CRO.
Misurazione della differenza di fase
Una figura di Lissajous viene visualizzata sullo schermo quando i segnali sinusoidali vengono applicati alle piastre di deflessione orizzontali e verticali del CRO. Quindi, applica i segnali sinusoidali, che hannosame amplitude and frequency sia alle piastre di deflessione orizzontali che verticali di CRO.
Per poche figure di Lissajous in base alla loro forma, possiamo dire direttamente la differenza di fase tra i due segnali sinusoidali.
Se la cifra di Lissajous è un straight line con un'inclinazione di $ 45 ^ {\ circ} $ con asse x positivo, quindi il phase differencetra i due segnali sinusoidali sarà $ 0 ^ {\ circ} $. Ciò significa che non c'è differenza di fase tra questi due segnali sinusoidali.
Se la cifra di Lissajous è un straight line con un'inclinazione di $ 135 ^ {\ circ} $ con asse x positivo, quindi il phase differencetra i due segnali sinusoidali sarà $ 180 ^ {\ circ} $. Ciò significa che quei due segnali sinusoidali sono sfasati.
Se la figura di Lissajous è in formato circular shape, allora la differenza di fase tra i due segnali sinusoidali sarà $ 90 ^ {\ circ} $ o $ 270 ^ {\ circ} $.
Possiamo calcolare la differenza di fase tra i due segnali sinusoidali usando formule, quando le cifre di Lissajous sono di elliptical shape.
Se l'asse maggiore di una figura di Lissajous di forma ellittica con un angolo di inclinazione si trova tra $ 0 ^ {\ circ} $ e $ 90 ^ {\ circ} $ con asse x positivo, allora la differenza di fase tra i due segnali sinusoidali sarà.
$$ \ phi = \ sin ^ {- 1} \ left (\ frac {x_ {1}} {x_ {2}} \ right) = \ sin ^ {- 1} \ left (\ frac {y_ {1} } {y_ {2}} \ right) $$
Se l'asse maggiore di una figura di Lissajous di forma ellittica con un angolo di inclinazione si trova tra $ 90 ^ {\ circ} $ e $ 180 ^ {\ circ} $ con asse x positivo, allora la differenza di fase tra i due segnali sinusoidali sarà.
$$ \ phi = 180 - \ sin ^ {- 1} \ left (\ frac {x_ {1}} {x_ {2}} \ right) = 180 - \ sin ^ {- 1} \ left (\ frac { y_ {1}} {y_ {2}} \ right) $$
Where,
$ x_ {1} $ è la distanza dall'origine al punto sull'asse x, dove si interseca la figura ellittica di Lissajous
$ x_ {2} $ è la distanza dall'origine alla tangente verticale della figura di Lissajous di forma ellittica
$ y_ {1} $ è la distanza dall'origine al punto sull'asse y, dove si interseca la figura ellittica di Lissajous
$ y_ {2} $ è la distanza dall'origine alla tangente orizzontale della figura di Lissajous di forma ellittica
In questo capitolo, imparerai come trovare la frequenza di un segnale sinusoidale sconosciuto e la differenza di fase tra due segnali sinusoidali dalle figure di Lissajous usando le formule.