Altri ponti AC

Nel capitolo precedente, abbiamo discusso di due ponti CA che possono essere utilizzati per misurare l'induttanza. In questo capitolo, discutiamo di quanto seguetwo AC bridges.

• Ponte Schering
• Ponte di Vienna

Questi due ponti possono essere utilizzati per misurare rispettivamente la capacità e la frequenza.

Ponte Schering

Il ponte di Schering è un ponte AC con quattro bracci, che sono collegati sotto forma di un rombo o square shape, il cui un braccio è costituito da un singolo resistore, un braccio è costituito da una combinazione in serie di resistore e condensatore, un braccio è costituito da un singolo condensatore e l'altro è costituito da una combinazione parallela di resistore e condensatore.

Il rilevatore AC e la sorgente di tensione AC sono anche usati per trovare il valore dell'impedenza sconosciuta, quindi uno di loro è posto in una diagonale del ponte di Schering e l'altro è posizionato nell'altra diagonale del ponte di Schering.

Il ponte di Schering viene utilizzato per misurare il valore della capacità. Ilcircuit diagram del ponte di Schering è mostrato nella figura sotto.

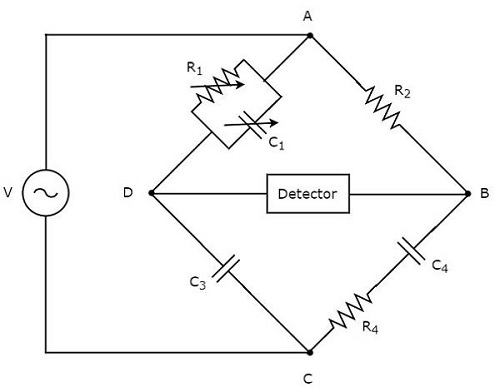
Nel circuito sopra, i bracci AB, BC, CD e DA formano insieme un rombo o square shape. Il braccio AB è costituito da una resistenza, $ R_ {2} $. Il braccio BC è costituito da una combinazione in serie di resistore, $ R_ {4} $ e condensatore, $ C_ {4} $. Il braccio CD è costituito da un condensatore, $ C_ {3} $. Il braccio DA è costituito da una combinazione parallela di resistore, $ R_ {1} $ e condensatore, $ C_ {1} $.

Siano, $ Z_ {1} $, $ Z_ {2} $, $ Z_ {3} $ e $ Z_ {4} $ rispettivamente le impedenze dei bracci DA, AB, CD e BC. Ilvalues of these impedances sarà

$ Z_ {1} = \ frac {R_ {1} \ left (\ frac {1} {j \ omega C_ {1}} \ right)} {R_ {1} + \ frac {1} {j \ omega C_ {1}}} $

$ \ Rightarrow Z_ {1} = \ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}} $

$ Z_ {2} = R_ {2} $

$ Z_ {3} = \ frac {1} {j \ omega C_ {3}} $

$ Z_ {4} = R_ {4} + \ frac {1} {j \ omega C_ {4}} $

$ \ Rightarrow Z_ {4} = \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} $

Substitute questi valori di impedenza nella seguente condizione di bilanciamento del ponte CA.

$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$

$$ \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} = \ frac {R_ {2} \ left (\ frac {1} {j \ omega C_ { 3}} \ right)} {\ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}} $$

$ \ Rightarrow \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} = \ frac {R_ {2} \ left (1 + j \ omega R_ {1} C_ {1} \ right)} {j \ omega R_ {1} C_ {3}} $

$ \ Rightarrow \ frac {1 + j \ omega R_ {4} C_ {4}} {C_ {4}} = \ frac {R_ {2} \ left (1 + j \ omega R_ {1} C_ {1} \ right)} {R_ {1} C_ {3}} $

$ \ Rightarrow \ frac {1} {C_ {4}} + j \ omega R_ {4} = \ frac {R_ {2}} {R_ {1} C_ {3}} + \ frac {j \ omega C_ { 1} R_ {2}} {C_ {3}} $

Di comparing i rispettivi termini reali e immaginari dell'equazione precedente, otterremo

$ C_ {4} = \ frac {R_ {1} C_ {3}} {R_ {2}} $ Equazione 1

$ R_ {4} = \ frac {C_ {1} R_ {2}} {C_ {3}} $ Equazione 2

Sostituendo i valori di $ R_ {1}, R_ {2} $ e $ C_ {3} $ nell'equazione 1, otterremo il valore del condensatore, $ C_ {4} $. Allo stesso modo, sostituendo i valori di $ R_ {2}, C_ {1} $ e $ C_ {3} $ nell'equazione 2, otterremo il valore del resistore, $ R_ {4} $.

Il advantage del ponte di Schering è che entrambi i valori del resistore, $ R_ {4} $ e del condensatore, $ C_ {4} $ sono indipendenti dal valore della frequenza.

Ponte di Vienna

Wien’s bridgeè un ponte AC con quattro bracci, che sono collegati a forma di rombo o di forma quadrata. Tra due bracci costituiti da un singolo resistore, un braccio è costituito da una combinazione parallela di resistore e condensatore e l'altro braccio è costituito da una combinazione in serie di resistore e condensatore.

Per trovare il valore della frequenza sono necessari anche il rilevatore AC e la sorgente di tensione AC. Quindi, uno di questi due è posto in una diagonale del ponte di Vienna e l'altro è posizionato nell'altra diagonale del ponte di Vienna.

Il circuit diagram del ponte di Vienna è mostrato nella figura sotto.

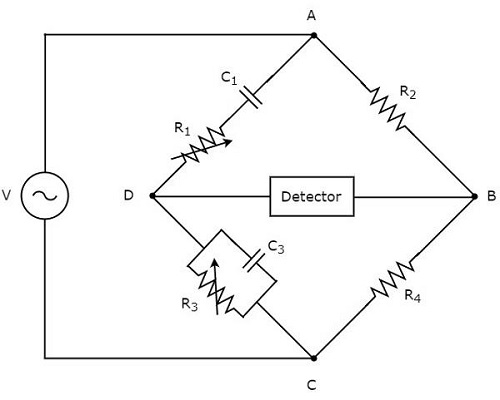
Nel circuito sopra, i bracci AB, BC, CD e DA formano insieme un rombo o square shape. I bracci, AB e BC sono costituiti da resistori, rispettivamente $ R_ {2} $ e $ R_ {4} $. Il braccio CD è costituito da una combinazione parallela di resistore, $ R_ {3} $ e condensatore, $ C_ {3} $. Il braccio DA è costituito da una combinazione in serie di resistore, $ R_ {1} $ e condensatore, $ C_ {1} $.

Siano, $ Z_ {1}, Z_ {2}, Z_ {3} $ e $ Z_ {4} $ sono le impedenze dei bracci DA, AB, CD e BC rispettivamente. Ilvalues of these impedances sarà

$$ Z_ {1} = R_ {1} + \ frac {1} {j \ omega C_ {1}} $$

$$ \ Rightarrow Z_ {1} = \ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} $$

$ Z_ {2} = R_ {2} $

$$ Z_ {3} = \ frac {R_ {3} \ left (\ frac {1} {j \ omega C_ {3}} \ right)} {R_ {3} + \ frac {1} {j \ omega C_ {3}}} $$

$$ \ Rightarrow Z_ {3} = \ frac {R_ {3}} {1 + j \ omega R_ {3} C_ {3}} $$

$ Z_ {4} = R_ {4} $

Substitute questi valori di impedenza nella seguente condizione di bilanciamento del ponte CA.

$$ Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $$

$$ \ left (\ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} \ right) R_ {4} = R_ {2} \ left (\ frac {R_ {3}} {1 + j \ omega R_ {3} C_ {3}} \ right) $$

$ \ Rightarrow \ left (1 + j \ omega R_ {1} C_ {1} \ right) \ left (1 + j \ omega R_ {3} C_ {3} \ right) R_ {4} = j \ omega C_ {1} R_ {2} R_ {3} $

$ \ Freccia destra \ sinistra (1 + j \ omega R_ {3} C_ {3} + j \ omega R_ {1} C_ {1} - \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ right) R_ {4} = j \ omega C_ {1} R_ {2} R_ {3} $

$ \ Rightarrow R_ {4} \ left (\ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ right) + j \ omega R_ {4} \ left (R_ {3} C_ {3} + R_ {1} C_ {1} \ right) = j \ omega C_ {1} R_ {2} R_ {3} $

Equate il rispettivo real terms dell'equazione precedente.

$$ R_ {4} \ left (1- \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ right) = 0 $$

$ \ Rightarrow 1- \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} = 0 $

$ \ Rightarrow 1 = \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} $

$ \ omega = \ frac {1} {\ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}} $

Substitute, $ \ omega = 2 \ pi f $ nell'equazione precedente.

$$ \ Rightarrow 2 \ pi f = \ frac {1} {\ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}} $$

$ \ Rightarrow f = \ frac {1} {2 \ pi \ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}} $

Possiamo trovare il valore della frequenza, $ f $ della sorgente di tensione CA sostituendo i valori di $ R_ {1}, R_ {3}, C_ {1} $ e $ C_ {3} $ nell'equazione precedente.

Se $ R_ {1} = R_ {3} = R $ e $ C_ {1} = C_ {3} = C $, allora possiamo trovare il valore della frequenza, $ f $ della sorgente di tensione CA utilizzando la seguente formula .

$$ f = \ frac {1} {2 \ pi RC} $$

Il ponte di Wein viene utilizzato principalmente per trovare il frequency value della gamma AF.