Tecniche di campionamento dei segnali
Esistono tre tipi di tecniche di campionamento:
Campionamento a impulsi.
Campionamento naturale.
Campionamento Flat Top.
Campionamento dell'impulso
Il campionamento degli impulsi può essere eseguito moltiplicando il segnale di ingresso x (t) per il treno di impulsi $ \ Sigma_ {n = - \ infty} ^ {\ infty} \ delta (t-nT) $ del periodo 'T'. Qui, l'ampiezza dell'impulso cambia rispetto all'ampiezza del segnale di ingresso x (t). L'output di sampler è dato da
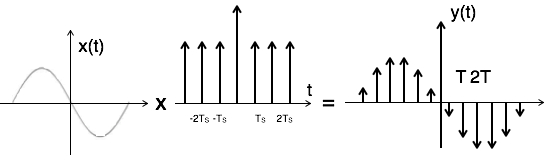
$ y (t) = x (t) × $ treno di impulsi
$ = x (t) × \ Sigma_ {n = - \ infty} ^ {\ infty} \ delta (t-nT) $
$ y (t) = y _ {\ delta} (t) = \ Sigma_ {n = - \ infty} ^ {\ infty} x (nt) \ delta (t-nT) \, ... \, ... 1 $
Per ottenere lo spettro del segnale campionato, si consideri la trasformata di Fourier dell'equazione 1 su entrambi i lati
$ Y (\ omega) = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} X (\ omega - n \ omega_s) $
Questo è chiamato campionamento ideale o campionamento a impulsi. Non è possibile utilizzarlo praticamente perché la larghezza dell'impulso non può essere zero e la generazione del treno di impulsi non è praticamente possibile.
Campionamento naturale
Il campionamento naturale è simile al campionamento a impulsi, tranne per il fatto che il treno di impulsi è sostituito dal treno di impulsi del periodo T. cioè moltiplichi il segnale di ingresso x (t) per il treno di impulsi $ \ Sigma_ {n = - \ infty} ^ {\ infty} P ( t-nT) $ come mostrato di seguito

L'output del campionatore è
$ y (t) = x (t) \ times \ text {treno di impulsi} $
$ = x (t) \ volte p (t) $
$ = x (t) \ times \ Sigma_ {n = - \ infty} ^ {\ infty} P (t-nT) \, ... \, ... (1) $
La rappresentazione in serie di Fourier esponenziale di p (t) può essere data come
$ p (t) = \ Sigma_ {n = - \ infty} ^ {\ infty} F_n e ^ {jn \ omega_s t} \, ... \, ... (2) $
$ = \ Sigma_ {n = - \ infty} ^ {\ infty} F_n e ^ {j 2 \ pi nf_s t} $
Dove $ F_n = {1 \ over T} \ int _ {- T \ over 2} ^ {T \ over 2} p (t) e ^ {- jn \ omega_s t} dt $
$ = {1 \ over TP} (n \ omega_s) $
Sostituisci il valore F n nell'equazione 2
$ \ quindi p (t) = \ Sigma_ {n = - \ infty} ^ {\ infty} {1 \ over T} P (n \ omega_s) e ^ {jn \ omega_s t} $
$ = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) e ^ {jn \ omega_s t} $
Sostituisci p (t) nell'equazione 1
$ y (t) = x (t) \ times p (t) $
$ = x (t) \ times {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, e ^ {jn \ omega_s t} $
$ y (t) = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, x (t) \, e ^ {jn \ omega_s t} $
Per ottenere lo spettro del segnale campionato, considerare la trasformata di Fourier su entrambi i lati.
$ FT \, [y (t)] = FT [{1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, x (t) \, e ^ { jn \ omega_s t}] $
$ = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, FT \, [x (t) \, e ^ {jn \ omega_s t}] $
Secondo la proprietà del cambio di frequenza
$ FT \, [x (t) \, e ^ {jn \ omega_s t}] = X [\ omega-n \ omega_s] $
$ \ quindi \, Y [\ omega] = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, X [\ omega-n \ omega_s] $
Campionamento Flat Top
Durante la trasmissione, viene introdotto del rumore nella parte superiore dell'impulso di trasmissione che può essere facilmente rimosso se l'impulso è sotto forma di sommità piatta. Qui, la parte superiore dei campioni è piatta, ovvero hanno un'ampiezza costante. Quindi, è chiamato campionamento flat top o campionamento pratico. Il campionamento flat top utilizza il circuito di campionamento e mantenimento.

Teoricamente, il segnale campionato può essere ottenuto mediante convoluzione dell'impulso rettangolare p (t) con segnale idealmente campionato diciamo y δ (t) come mostrato nel diagramma:
cioè $ y (t) = p (t) \ times y_ \ delta (t) \, ... \, ... (1) $

Per ottenere lo spettro campionato, considera la trasformata di Fourier su entrambi i lati per l'equazione 1
$ Y [\ omega] = FT \, [P (t) \ times y_ \ delta (t)] $
Con la conoscenza della proprietà di convoluzione,
$ Y [\ omega] = P (\ omega) \, Y_ \ delta (\ omega) $
Qui $ P (\ omega) = T Sa ({\ omega T \ over 2}) = 2 \ sin \ omega T / \ omega $
Tasso di Nyquist
È la frequenza di campionamento minima alla quale il segnale può essere convertito in campioni e può essere recuperato senza distorsioni.
Tasso di Nyquist f N = 2f m hz
Intervallo di Nyquist = $ {1 \ over fN} $ = $ {1 \ over 2fm} $ secondi.
Campionamenti di segnali Band Pass
In caso di segnali passa banda, lo spettro del segnale passa banda X [ω] = 0 per le frequenze al di fuori dell'intervallo f 1 ≤ f ≤ f 2 . La frequenza f 1 è sempre maggiore di zero. Inoltre, non vi è alcun effetto di aliasing quando f s > 2f 2 . Ma ha due svantaggi:
La frequenza di campionamento è grande in proporzione a f 2 . Questo ha dei limiti pratici.
Lo spettro del segnale campionato ha lacune spettrali.
Per ovviare a questo, il teorema passa banda afferma che il segnale di ingresso x (t) può essere convertito nei suoi campioni e può essere recuperato senza distorsione quando si campiona la frequenza f s <2f 2 .
Anche,
$$ f_s = {1 \ over T} = {2f_2 \ over m} $$
Dove m è il numero intero più grande <$ {f_2 \ su B} $
e B è la larghezza di banda del segnale. Se f 2 = KB, allora
$$ f_s = {1 \ over T} = {2KB \ over m} $$
Per i segnali passa banda con larghezza di banda 2f m e la frequenza di campionamento minima f s = 2 B = 4f m ,
lo spettro del segnale campionato è dato da $ Y [\ omega] = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} \, X [\ omega - 2nB] $