Proprietà delle trasformazioni Z.

Z-Transform ha le seguenti proprietà:

Proprietà di linearità

Se $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

e $ \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z) $

Quindi la proprietà di linearità lo afferma

$ a \, x (n) + b \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} a \, X (Z) + b \, Y (Z) $

Proprietà Time Shifting

Se $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

Quindi la proprietà Time shifting lo afferma

$ x (nm) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} z ^ {- m} X (Z) $

Moltiplicazione per proprietà della sequenza esponenziale

Se $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

Quindi la moltiplicazione per una proprietà di sequenza esponenziale lo afferma

$ a ^ n \,. x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z / a) $

Proprietà di inversione temporale

Se $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

Quindi la proprietà di inversione temporale lo afferma

$ x (-n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (1 / Z) $

Differenziazione nel dominio Z OR Moltiplicazione per n proprietà

Se $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

Quindi la moltiplicazione per n o la differenziazione nella proprietà del dominio z lo afferma

$ n ^ kx (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} [-1] ^ kz ^ k {d ^ k X (Z) \ over dZ ^ K} $

Proprietà di convoluzione

Se $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

e $ \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z) $

Quindi la proprietà di convoluzione lo afferma

$ x (n) * y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) .Y (Z) $

Proprietà di correlazione

Se $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

e $ \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z) $

Quindi la proprietà di correlazione lo afferma

$ x (n) \ otimes y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) .Y (Z ^ {- 1}) $

Teoremi del valore iniziale e del valore finale

I teoremi del valore iniziale e del valore finale della trasformata z sono definiti per il segnale causale.

Teorema del valore iniziale

Per un segnale causale x (n), il teorema del valore iniziale lo afferma

$ x (0) = \ lim_ {z \ to \ infty} ⁡X (z) $

Viene utilizzato per trovare il valore iniziale del segnale senza prendere la trasformata z inversa

Teorema del valore finale

Per un segnale causale x (n), il teorema del valore finale lo afferma

$ x (\ infty) = \ lim_ {z \ to 1} [z-1] ⁡X (z) $

Questo è usato per trovare il valore finale del segnale senza prendere la trasformata z inversa.

Regione di Convergenza (ROC) di Z-Transform

L'intervallo di variazione di z per cui converge la trasformata z è chiamato regione di convergenza della trasformata z.

Proprietà del ROC delle trasformate Z.

Il ROC della trasformata z è indicato con un cerchio nel piano z.
ROC non contiene pali.
Se x (n) è una sequenza causale di durata finita o una sequenza del lato destro, allora il ROC è l'intero piano z eccetto per z = 0.
Se x (n) è una sequenza anti-causale di durata finita o una sequenza del lato sinistro, allora il ROC è l'intero piano z tranne che in z = ∞.
Se x (n) è una sequenza causale di durata infinita, ROC è esterno al cerchio con raggio aie | z | > a.
Se x (n) è una sequenza anti-causale di durata infinita, ROC è l'interno del cerchio con raggio aie | z | <a.
Se x (n) è una sequenza a due lati di durata finita, il ROC è l'intero piano z eccetto per z = 0 & z = ∞.

Il concetto di ROC può essere spiegato dal seguente esempio:

Example 1: Trova la trasformazione Z e il ROC di $ a ^ nu [n] + a ^ {-} nu [-n-1] $

$ ZT [a ^ nu [n]] + ZT [a ^ {- n} u [-n-1]] = {Z \ over Za} + {Z \ over Z {-1 \ over a}} $

$$ ROC: | z | \ gt a \ quad \ quad ROC: | z | \ lt {1 \ su un} $$

Il grafico di ROC ha due condizioni come a> 1 e a <1, poiché non conosci a.

In questo caso, non esiste una combinazione ROC.

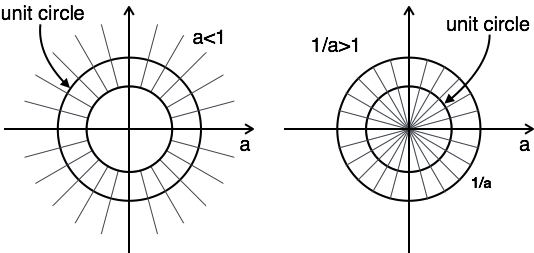
Qui, la combinazione di ROC è da $ a \ lt | z | \ lt {1 \ su un} $

Quindi per questo problema, la trasformazione z è possibile quando a <1.

Causalità e stabilità

La condizione di causalità per i sistemi LTI a tempo discreto è la seguente:

Un sistema LTI a tempo discreto è causale quando

ROC è al di fuori del polo più esterno.
Nella funzione di trasferimento H [Z], l'ordine del numeratore non può essere superiore all'ordine del denominatore.

Condizione di stabilità per sistemi LTI a tempo discreto

Un sistema LTI a tempo discreto è stabile quando

la sua funzione di sistema H [Z] include il cerchio unitario | z | = 1.
tutti i poli della funzione di trasferimento si trovano all'interno del cerchio unitario | z | = 1.

Trasformata Z dei segnali di base

x (t)	X [Z]
$ \ delta $	1
$ u (n) $	$ {Z \ over Z-1} $
$ u (-n-1) $	$ - {Z \ over Z-1} $
$ \ delta (nm) $	$ z ^ {- m} $
$ a ^ nu [n] $	$ {Z \ over Za} $
$ a ^ nu [-n-1] $	$ - {Z \ over Za} $
$ n \, a ^ nu [n] $	$ {aZ \ over \| Za \| ^ 2} $
$ n \, a ^ nu [-n-1] $	$ - {aZ \ over \| Za \| ^ 2} $
$ a ^ n \ cos \ omega nu [n] $	$ {Z ^ 2-aZ \ cos \ omega \ over Z ^ 2-2aZ \ cos \ omega + a ^ 2} $
$ a ^ n \ sin \ omega nu [n] $	$ {aZ \ sin \ omega \ over Z ^ 2 -2aZ \ cos \ omega + a ^ 2} $