ビッグデータ分析-クイックガイド
処理しなければならないデータの量は、過去10年間で想像を絶するレベルにまで爆発的に増加し、同時に、データストレージの価格は体系的に削減されました。民間企業や研究機関は、ユーザーのインタラクション、ビジネス、ソーシャルメディア、さらには携帯電話や自動車などのデバイスからのセンサーに関するテラバイトのデータをキャプチャします。この時代の課題は、このデータの海を理解することです。ここがbig data analytics 絵になります。
ビッグデータ分析では、主にさまざまなソースからデータを収集し、アナリストが利用できるようにデータを管理し、最終的に組織のビジネスに役立つデータ製品を提供します。

さまざまなソースから取得した大量の非構造化生データを組織に役立つデータ製品に変換するプロセスは、ビッグデータ分析の中核を形成します。
従来のデータマイニングのライフサイクル
組織が必要とする作業を整理し、ビッグデータから明確な洞察を提供するためのフレームワークを提供するには、それをさまざまな段階のサイクルと考えると便利です。これは決して線形ではありません。つまり、すべてのステージが相互に関連しています。このサイクルは、で説明されているように、従来のデータマイニングサイクルと表面的に類似しています。CRISP methodology。
CRISP-DM方法論
ザ・ CRISP-DM methodologyこれは、データマイニングの業界標準プロセスの略で、データマイニングの専門家が従来のBIデータマイニングの問題に取り組むために使用する一般的に使用されるアプローチを説明するサイクルです。従来のBIデータマイニングチームで引き続き使用されています。
次の図を見てください。これは、CRISP-DM方法論で説明されているサイクルの主要な段階と、それらがどのように相互に関連しているかを示しています。
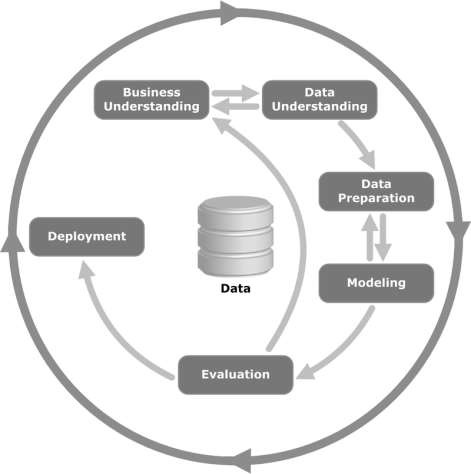
CRISP-DMは1996年に考案され、翌年、ESPRITの資金提供イニシアチブの下で欧州連合のプロジェクトとして開始されました。このプロジェクトは、SPSS、Teradata、Daimler AG、NCR Corporation、およびOHRA(保険会社)の5社が主導しました。プロジェクトは最終的にSPSSに組み込まれました。方法論は、データマイニングプロジェクトをどのように指定するかという点で非常に詳細です。
ここで、CRISP-DMライフサイクルに含まれる各段階についてもう少し学びましょう。
Business Understanding−この初期段階では、ビジネスの観点からプロジェクトの目的と要件を理解し、この知識をデータマイニングの問題定義に変換することに重点を置いています。予備計画は、目的を達成するために設計されています。意思決定モデル、特に意思決定モデルと表記法の標準を使用して構築されたモデルを使用できます。
Data Understanding −データ理解フェーズは、最初のデータ収集から始まり、データに精通し、データ品質の問題を特定し、データへの最初の洞察を発見し、または興味深いサブセットを検出して隠された情報の仮説を立てるためのアクティビティに進みます。
Data Preparation−データ準備フェーズでは、最初の生データから最終データセット(モデリングツールに入力されるデータ)を構築するためのすべてのアクティビティをカバーします。データ準備タスクは、指定された順序ではなく、複数回実行される可能性があります。タスクには、テーブル、レコード、属性の選択、およびモデリングツールのデータの変換とクリーニングが含まれます。
Modeling−このフェーズでは、さまざまなモデリング手法が選択および適用され、それらのパラメーターが最適値に調整されます。通常、同じデータマイニングの問題タイプにはいくつかの手法があります。一部の手法には、データの形式に関する特定の要件があります。したがって、多くの場合、データ準備フェーズに戻る必要があります。
Evaluation−プロジェクトのこの段階で、データ分析の観点から、高品質に見える1つまたは複数のモデルを作成しました。モデルの最終的な展開に進む前に、モデルを徹底的に評価し、モデルを構築するために実行された手順を確認して、ビジネス目標が適切に達成されていることを確認することが重要です。
主な目的は、十分に考慮されていない重要なビジネス上の問題があるかどうかを判断することです。このフェーズの終わりに、データマイニング結果の使用に関する決定に達する必要があります。
Deployment−モデルの作成は、通常、プロジェクトの終わりではありません。モデルの目的がデータの知識を増やすことである場合でも、得られた知識は、顧客にとって有用な方法で編成および提示される必要があります。
要件に応じて、展開フェーズは、レポートの生成のように単純な場合もあれば、繰り返し可能なデータスコアリング(セグメント割り当てなど)またはデータマイニングプロセスの実装のように複雑な場合もあります。
多くの場合、展開手順を実行するのはデータアナリストではなく、顧客です。アナリストがモデルを展開する場合でも、作成されたモデルを実際に利用するために実行する必要のあるアクションを顧客が事前に理解することが重要です。
SEMMA方法論
SEMMAは、データマイニングモデリングのためにSASによって開発されたもう1つの方法です。それはの略ですS十分な、 Explore、 Modify、 Model、および Asses。これがその段階の簡単な説明です-
Sample−プロセスは、データのサンプリングから始まります。たとえば、モデリング用のデータセットを選択します。データセットは、取得するのに十分な情報を含むのに十分な大きさでありながら、効率的に使用するのに十分な小ささである必要があります。このフェーズでは、データのパーティション化も扱います。
Explore −このフェーズでは、データの視覚化を利用して、変数間の予期される関係と予期されない関係、および異常を発見することにより、データの理解をカバーします。
Modify −変更フェーズには、データモデリングの準備として変数を選択、作成、および変換するメソッドが含まれています。
Model −モデルフェーズでは、目的の結果を提供する可能性のあるモデルを作成するために、準備された変数にさまざまなモデリング(データマイニング)手法を適用することに重点が置かれます。
Assess −モデリング結果の評価は、作成されたモデルの信頼性と有用性を示しています。
CRISM-DMとSEMMAの主な違いは、SEMMAはモデリングの側面に焦点を当てているのに対し、CRISP-DMは、解決すべきビジネス上の問題の理解、データの理解と前処理など、モデリング前のサイクルの段階をより重要視していることです。機械学習アルゴリズムなどの入力として使用されます。
ビッグデータのライフサイクル
今日のビッグデータのコンテキストでは、以前のアプローチは不完全であるか、最適ではありません。たとえば、SEMMA方法論は、さまざまなデータソースのデータ収集と前処理を完全に無視します。これらの段階は通常、成功するビッグデータプロジェクトのほとんどの作業を構成します。
ビッグデータ分析サイクルは、次の段階で説明できます。
- ビジネス上の問題の定義
- Research
- 人事評価
- データ収集
- データの変更
- データストレージ
- 探索的データ分析
- モデリングと評価のためのデータ準備
- Modeling
- Implementation
このセクションでは、ビッグデータのライフサイクルのこれらの各段階に光を当てます。
ビジネス上の問題の定義
これは、従来のBIおよびビッグデータ分析のライフサイクルに共通するポイントです。通常、問題を定義し、組織にとってどれだけの潜在的な利益が得られるかを正しく評価することは、ビッグデータプロジェクトの重要な段階です。これに言及するのは明らかなようですが、プロジェクトの期待される利益とコストを評価する必要があります。
研究
同じ状況で他の企業が行ったことを分析します。これには、会社が持っているリソースや要件に他のソリューションを適応させる必要がある場合でも、会社にとって合理的なソリューションを探すことが含まれます。この段階では、将来の段階の方法論を定義する必要があります。
人事評価
問題が定義されたら、現在のスタッフがプロジェクトを正常に完了できるかどうかを分析し続けるのが妥当です。従来のBIチームは、すべての段階に最適なソリューションを提供できない可能性があるため、プロジェクトの一部を外部委託したり、より多くの人を雇ったりする必要がある場合は、プロジェクトを開始する前に検討する必要があります。
データ収集
このセクションは、ビッグデータのライフサイクルにおいて重要です。結果のデータ製品を配信するために必要なプロファイルのタイプを定義します。データ収集は、プロセスの重要なステップです。通常、さまざまなソースから非構造化データを収集する必要があります。例を挙げると、Webサイトからレビューを取得するクローラーを作成する必要があります。これには、おそらく異なる言語でのテキストの処理が含まれ、通常、完了するまでにかなりの時間が必要です。
データの変更
たとえば、Webからデータを取得したら、使いやすい形式で保存する必要があります。レビューの例を続けるために、データが異なるサイトから取得され、それぞれが異なる表示のデータを持っていると仮定しましょう。
1つのデータソースが星の評価に関してレビューを提供するとします。したがって、これを応答変数のマッピングとして読み取ることができます。 y ∈ {1, 2, 3, 4, 5}。別のデータソースは、2つの矢印システムを使用してレビューを提供します。1つは賛成票、もう1つは反対票です。これは、次の形式の応答変数を意味しますy ∈ {positive, negative}。
両方のデータソースを組み合わせるには、これら2つの応答表現を同等にするための決定を行う必要があります。これには、1つの星を負、5つの星を正と見なして、最初のデータソース応答表現を2番目の形式に変換することが含まれます。このプロセスでは、多くの場合、高品質で配信するために多大な時間の割り当てが必要になります。
データストレージ
データが処理されると、データベースに保存する必要がある場合があります。ビッグデータテクノロジーは、この点に関して多くの選択肢を提供します。最も一般的な代替手段は、HIVEクエリ言語と呼ばれる限定バージョンのSQLをユーザーに提供するストレージにHadoopファイルシステムを使用することです。これにより、ユーザーの観点から、ほとんどの分析タスクを従来のBIデータウェアハウスで実行されるのと同様の方法で実行できます。考慮すべき他のストレージオプションは、MongoDB、Redis、およびSPARKです。
サイクルのこの段階は、さまざまなアーキテクチャを実装する能力という点で、人事の知識に関連しています。従来のデータウェアハウスの修正バージョンは、依然として大規模なアプリケーションで使用されています。たとえば、teradataとIBMは、テラバイトのデータを処理できるSQLデータベースを提供しています。postgreSQLやMySQLなどのオープンソースソリューションは、現在も大規模なアプリケーションに使用されています。
さまざまなストレージがバックグラウンドでどのように機能するかには違いがありますが、クライアント側から見ると、ほとんどのソリューションはSQLAPIを提供します。したがって、SQLを十分に理解することは、ビッグデータ分析にとって依然として重要なスキルです。
この段階は先験的に最も重要なトピックのようですが、実際にはそうではありません。それは本質的な段階でさえありません。リアルタイムデータを処理するビッグデータソリューションを実装することは可能であるため、この場合、モデルを開発するためにデータを収集し、それをリアルタイムで実装するだけで済みます。したがって、データを正式に保存する必要はまったくありません。
探索的データ分析
データがクリーンアップされ、そこから洞察を取得できるように保存されたら、データ探索フェーズは必須です。この段階の目的は、データを理解することです。これは通常、統計的手法を使用して行われ、データをプロットします。これは、問題の定義が理にかなっているか、実行可能かを評価するのに適した段階です。
モデリングと評価のためのデータ準備
この段階では、以前に取得したクリーンなデータを再形成し、欠測値の代入、外れ値の検出、正規化、特徴抽出、特徴選択のための統計的前処理を使用します。
モデリング
前の段階では、予測モデルなど、トレーニングとテスト用のいくつかのデータセットを作成する必要がありました。この段階では、さまざまなモデルを試し、目前のビジネス上の問題を解決することを楽しみにしています。実際には、通常、モデルがビジネスへの洞察を与えることが望まれます。最後に、除外されたデータセットでのパフォーマンスを評価するために、最適なモデルまたはモデルの組み合わせが選択されます。
実装
この段階で、開発されたデータ製品は会社のデータパイプラインに実装されます。これには、データ製品のパフォーマンスを追跡するために、データ製品の動作中に検証スキームを設定することが含まれます。たとえば、予測モデルを実装する場合、この段階では、モデルを新しいデータに適用し、応答が利用可能になったら、モデルを評価します。
方法論の点では、ビッグデータ分析は実験計画の従来の統計的アプローチとは大きく異なります。分析はデータから始まります。通常、応答を説明する方法でデータをモデル化します。このアプローチの目的は、応答の動作を予測すること、または入力変数が応答にどのように関連するかを理解することです。通常、統計実験計画では、実験が開発され、結果としてデータが取得されます。これにより、独立性、正規性、ランダム化などの特定の仮定が成り立つ統計モデルで使用できる方法でデータを生成できます。
ビッグデータ分析では、データが提示されます。お気に入りの統計モデルを満たす実験を設計することはできません。分析の大規模なアプリケーションでは、データをクリーンアップするためだけに大量の作業(通常は作業の80%)が必要になるため、機械学習モデルで使用できます。
実際の大規模アプリケーションで従うべき独自の方法論はありません。通常、ビジネス上の問題が定義されたら、使用する方法論を設計するための調査段階が必要です。ただし、一般的なガイドラインは言及するのに関連しており、ほとんどすべての問題に適用されます。
ビッグデータ分析で最も重要なタスクの1つは statistical modeling、教師ありおよび教師なしの分類または回帰の問題を意味します。データがクリーンアップされて前処理され、モデリングに使用できるようになったら、妥当な損失メトリックを使用してさまざまなモデルを評価する際に注意を払う必要があります。モデルが実装されたら、さらに評価と結果を報告する必要があります。予測モデリングの一般的な落とし穴は、モデルを実装するだけで、そのパフォーマンスを測定しないことです。
ビッグデータのライフサイクルで述べたように、ビッグデータ製品の開発から生じるデータ製品は、ほとんどの場合、次のようなものです。
Machine learning implementation −これは、分類アルゴリズム、回帰モデル、またはセグメンテーションモデルである可能性があります。
Recommender system −目的は、ユーザーの行動に基づいて選択を推奨するシステムを開発することです。 Netflix はこのデータ製品の特徴的な例であり、ユーザーの評価に基づいて他の映画が推奨されます。
Dashboard−通常、ビジネスには、集約されたデータを視覚化するためのツールが必要です。ダッシュボードは、このデータにアクセスできるようにするためのグラフィカルなメカニズムです。
Ad-Hoc analysis −通常、事業領域には、データを使用したアドホック分析を行うことで回答できる質問、仮説、または神話があります。
大規模な組織では、ビッグデータプロジェクトの開発を成功させるには、プロジェクトをバックアップする管理者が必要です。これには通常、プロジェクトのビジネス上の利点を示す方法を見つけることが含まれます。プロジェクトのスポンサーを見つけるという問題に対する独自の解決策はありませんが、いくつかのガイドラインを以下に示します。
興味のあるプロジェクトと同様の他のプロジェクトのスポンサーが誰でどこにいるかを確認してください。
主要な管理職に個人的な連絡先を置くことは役立つので、プロジェクトが有望である場合は、あらゆる連絡先をトリガーできます。
あなたのプロジェクトから誰が恩恵を受けますか?プロジェクトが軌道に乗ったら、誰があなたのクライアントになりますか?
シンプルで明確な既存の提案を作成し、組織の主要なプレーヤーと共有します。
プロジェクトのスポンサーを見つける最良の方法は、問題と、それが実装された後の結果のデータ製品がどうなるかを理解することです。この理解は、ビッグデータプロジェクトの重要性を経営陣に納得させる上で優位に立つでしょう。
データアナリストは、SQLを使用して従来のデータウェアハウスからデータを抽出および分析した経験を持つ、レポート指向のプロファイルを持っています。彼らの仕事は通常、データストレージの側か、一般的なビジネス結果の報告のいずれかです。データウェアハウジングは決して単純なものではなく、データサイエンティストが行うこととはまったく異なります。
多くの組織は、市場で有能なデータサイエンティストを見つけるのに苦労しています。ただし、将来のデータアナリストを選択し、データサイエンティストになるための関連スキルを教えることをお勧めします。これは決して些細な作業ではなく、通常、量的分野で修士号を取得している人が関与しますが、それは間違いなく実行可能なオプションです。有能なデータアナリストが持つ必要のある基本的なスキルを以下に示します-
- ビジネスの理解
- SQLプログラミング
- レポートの設計と実装
- ダッシュボード開発
データサイエンティストの役割は、通常、予測モデリング、セグメンテーションアルゴリズムの開発、レコメンダーシステム、A / Bテストフレームワークなどのタスクに関連付けられており、多くの場合、生の非構造化データを処理します。
彼らの仕事の性質上、数学、応用統計、プログラミングについての深い理解が必要です。データアナリストとデータサイエンティストに共通するスキルがいくつかあります。たとえば、データベースにクエリを実行する機能などです。どちらもデータを分析しますが、データサイエンティストの決定は、組織に大きな影響を与える可能性があります。
これは、データサイエンティストが通常持つ必要のある一連のスキルです-
- R、Python、SAS、SPSS、Juliaなどの統計パッケージでのプログラミング
- さまざまなソースからのデータをクリーンアップ、抽出、および探索できる
- 統計モデルの調査、設計、および実装
- 統計、数学、コンピューターサイエンスに関する深い知識
ビッグデータ分析では、人々は通常、データサイエンティストの役割とデータアーキテクトの役割を混同します。実際には、違いは非常に単純です。データアーキテクトはデータが保存されるツールとアーキテクチャを定義しますが、データサイエンティストはこのアーキテクチャを使用します。もちろん、データサイエンティストは、アドホックプロジェクトに必要な場合は新しいツールをセットアップできるはずですが、インフラストラクチャの定義と設計は彼のタスクの一部であってはなりません。
このチュートリアルを通じて、プロジェクトを開発します。このチュートリアルの後続の各章では、ミニプロジェクトセクションのより大きなプロジェクトの一部を扱います。これは、実際の問題への露出を提供する応用チュートリアルセクションであると考えられています。この場合、プロジェクトの問題定義から始めます。
プロジェクトの説明
このプロジェクトの目的は、履歴書(CV)テキストを入力として使用して、人々の時給を予測する機械学習モデルを開発することです。
上で定義したフレームワークを使用すると、問題を簡単に定義できます。X = {x 1、x 2、…、x n }をユーザーのCVとして定義できます。ここで、各機能は、可能な限り簡単な方法で、この単語が表示される回数にすることができます。次に、応答は実際に評価されます。私たちは、個人の時給をドルで予測しようとしています。
これらの2つの考慮事項は、提示された問題が教師あり回帰アルゴリズムで解決できると結論付けるのに十分です。
問題の定義
Problem Definitionおそらく、ビッグデータ分析パイプラインで最も複雑で無視されがちな段階の1つです。データ製品が解決する問題を定義するには、経験が必須です。ほとんどのデータサイエンティスト志願者は、この段階でほとんどまたはまったく経験がありません。
ほとんどのビッグデータの問題は、次の方法で分類できます-
- 教師あり分類
- 教師あり回帰
- 教師なし学習
- ランク付けを学ぶ
ここで、これら4つの概念について詳しく学びましょう。
教師あり分類
機能の行列所与X = {X 1とx 2、...、xはN }我々はとして定義され、異なるクラス予測するモデルMを開発Y = {C 1、C 2、...、C N }を。例:保険会社の顧客のトランザクションデータが与えられると、クライアントが解約するかどうかを予測するモデルを開発することができます。後者はバイナリ分類の問題であり、チャーンとチャーンではない2つのクラスまたはターゲット変数があります。
他の問題には、複数のクラスの予測が含まれます。数字認識を行うことに関心がある可能性があるため、応答ベクトルは次のように定義されます。y= {0、1、2、3、4、5、6、7、8、9}、最先端のモデルは畳み込みニューラルネットワークであり、特徴のマトリックスは画像のピクセルとして定義されます。
教師あり回帰
この場合、問題の定義は前の例とかなり似ています。違いは応答に依存します。回帰問題では、応答y∈ℜ、これは応答が実数値であることを意味します。たとえば、履歴書のコーパスが与えられた個人の時給を予測するモデルを開発できます。
教師なし学習
経営陣はしばしば新しい洞察を渇望しています。セグメンテーションモデルは、マーケティング部門がさまざまなセグメントの製品を開発するために、この洞察を提供できます。アルゴリズムを考えるのではなく、セグメンテーションモデルを開発するための優れたアプローチは、必要なセグメンテーションに関連する機能を選択することです。
たとえば、電気通信会社では、携帯電話の使用状況によってクライアントをセグメント化するのは興味深いことです。これには、セグメンテーションの目的とは関係のない機能を無視し、関係する機能のみを含めることが含まれます。この場合、これは、1か月に使用されるSMSの数、インバウンドとアウトバウンドの分数などの機能を選択することになります。
ランク付けを学ぶ
この問題は回帰問題と見なすことができますが、特定の特性があり、別の処理に値します。問題は、クエリで最も関連性の高い順序を見つけようとするドキュメントのコレクションを指定することです。教師あり学習アルゴリズムを開発するには、クエリを指定して、順序付けの関連性にラベルを付ける必要があります。
教師あり学習アルゴリズムを開発するには、トレーニングデータにラベルを付ける必要があることに注意してください。これは、たとえば画像から数字を認識するモデルをトレーニングするには、かなりの量の例に手作業でラベルを付ける必要があることを意味します。このプロセスを高速化できるWebサービスがあり、Amazon MechanicalTurkなどのこのタスクに一般的に使用されています。学習アルゴリズムは、より多くのデータが提供されるとパフォーマンスが向上することが証明されているため、教師あり学習では、適切な量の例にラベルを付けることが事実上必須です。
データ収集は、ビッグデータサイクルで最も重要な役割を果たします。インターネットは、さまざまなトピックについてほぼ無制限のデータソースを提供します。この分野の重要性はビジネスの種類によって異なりますが、従来の業界では、さまざまな外部データのソースを取得し、それらをトランザクションデータと組み合わせることができます。
たとえば、レストランを推薦するシステムを構築したいとします。最初のステップは、データ(この場合はさまざまなWebサイトからレストランのレビュー)を収集し、それらをデータベースに保存することです。生のテキストに関心があり、それを分析に使用するため、モデルを開発するためのデータがどこに保存されるかはそれほど重要ではありません。これはビッグデータのメインテクノロジーと矛盾しているように聞こえるかもしれませんが、ビッグデータアプリケーションを実装するには、それをリアルタイムで機能させる必要があります。
Twitterミニプロジェクト
問題が定義されたら、次の段階はデータを収集することです。次のミニプロジェクトのアイデアは、Webからデータを収集し、機械学習モデルで使用できるように構造化することです。Rプログラミング言語を使用してTwitterRESTAPIからいくつかのツイートを収集します。
まずTwitterアカウントを作成し、次に twitteRTwitter開発者アカウントを作成するためのパッケージビネット。これはそれらの指示の要約です-
に移動 https://twitter.com/apps/new とログインします。
基本情報を入力したら、[設定]タブに移動し、[ダイレクトメッセージの読み取り、書き込み、アクセス]を選択します。
これを行った後、必ず保存ボタンをクリックしてください
[詳細]タブで、コンシューマーキーとコンシューマーシークレットをメモします
Rセッションでは、APIキーとAPIシークレット値を使用します
最後に、次のスクリプトを実行します。これにより、twitteR githubのリポジトリからパッケージ。
install.packages(c("devtools", "rjson", "bit64", "httr"))
# Make sure to restart your R session at this point
library(devtools)
install_github("geoffjentry/twitteR")文字列「bigmac」が含まれているデータを取得し、これについてどのトピックが目立つかを調べることに関心があります。これを行うための最初のステップは、Twitterからデータを収集することです。以下は、Twitterから必要なデータを収集するためのRスクリプトです。このコードは、bda / part1 / collect_data /collect_data_twitter.Rファイルでも入手できます。
rm(list = ls(all = TRUE)); gc() # Clears the global environment
library(twitteR)
Sys.setlocale(category = "LC_ALL", locale = "C")
### Replace the xxx’s with the values you got from the previous instructions
# consumer_key = "xxxxxxxxxxxxxxxxxxxx"
# consumer_secret = "xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"
# access_token = "xxxxxxxxxx-xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"
# access_token_secret= "xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"
# Connect to twitter rest API
setup_twitter_oauth(consumer_key, consumer_secret, access_token, access_token_secret)
# Get tweets related to big mac
tweets <- searchTwitter(’big mac’, n = 200, lang = ’en’)
df <- twListToDF(tweets)
# Take a look at the data
head(df)
# Check which device is most used
sources <- sapply(tweets, function(x) x$getStatusSource())
sources <- gsub("</a>", "", sources)
sources <- strsplit(sources, ">")
sources <- sapply(sources, function(x) ifelse(length(x) > 1, x[2], x[1]))
source_table = table(sources)
source_table = source_table[source_table > 1]
freq = source_table[order(source_table, decreasing = T)]
as.data.frame(freq)
# Frequency
# Twitter for iPhone 71
# Twitter for Android 29
# Twitter Web Client 25
# recognia 20データが収集されると、通常、さまざまな特性を持つさまざまなデータソースがあります。最も直接的なステップは、これらのデータソースを同種にし、データ製品の開発を継続することです。ただし、データの種類によって異なります。データを均質化することが実際的かどうかを自問する必要があります。
たぶん、データソースは完全に異なり、ソースが均質化されると情報の損失が大きくなります。この場合、代替案を考えることができます。1つのデータソースは回帰モデルの構築に役立ち、もう1つのデータソースは分類モデルの構築に役立ちますか?情報を失うだけでなく、私たちの利益のために異質性に取り組むことは可能ですか?これらの決定を下すことは、分析を面白くてやりがいのあるものにします。
レビューの場合、データソースごとに言語を設定することができます。繰り返しますが、2つの選択肢があります-
Homogenization−さまざまな言語を、より多くのデータがある言語に翻訳する必要があります。翻訳サービスの品質は許容範囲内ですが、APIを使用して大量のデータを翻訳する場合は、かなりのコストがかかります。このタスクに使用できるソフトウェアツールはありますが、それもコストがかかります。
Heterogenization−各言語のソリューションを開発することは可能でしょうか?コーパスの言語を簡単に検出できるため、言語ごとにレコメンダーを作成できます。これには、利用可能な言語の量に応じて各レコメンダーを調整するという点でより多くの作業が必要になりますが、利用可能な言語がいくつかある場合は間違いなく実行可能なオプションです。
Twitterミニプロジェクト
この場合、トピックモデリングを適用するために、最初に非構造化データをクリーンアップしてから、データマトリックスに変換する必要があります。一般に、Twitterからデータを取得する場合、少なくともデータクレンジングプロセスの最初の段階では、使用したくない文字がいくつかあります。
たとえば、ツイートを取得すると、「<ed> <U + 00A0> <U + 00BD> <ed> <U + 00B8> <U + 008B>」という奇妙な文字が表示されます。これらはおそらく絵文字であるため、データをクリーンアップするために、次のスクリプトを使用してそれらを削除します。このコードは、bda / part1 / collect_data /cleaning_data.Rファイルでも入手できます。
rm(list = ls(all = TRUE)); gc() # Clears the global environment
source('collect_data_twitter.R')
# Some tweets
head(df$text)
[1] "I’m not a big fan of turkey but baked Mac &
cheese <ed><U+00A0><U+00BD><ed><U+00B8><U+008B>"
[2] "@Jayoh30 Like no special sauce on a big mac. HOW"
### We are interested in the text - Let’s clean it!
# We first convert the encoding of the text from latin1 to ASCII
df$text <- sapply(df$text,function(row) iconv(row, "latin1", "ASCII", sub = ""))
# Create a function to clean tweets
clean.text <- function(tx) {
tx <- gsub("htt.{1,20}", " ", tx, ignore.case = TRUE)
tx = gsub("[^#[:^punct:]]|@|RT", " ", tx, perl = TRUE, ignore.case = TRUE)
tx = gsub("[[:digit:]]", " ", tx, ignore.case = TRUE)
tx = gsub(" {1,}", " ", tx, ignore.case = TRUE)
tx = gsub("^\\s+|\\s+$", " ", tx, ignore.case = TRUE) return(tx) } clean_tweets <- lapply(df$text, clean.text)
# Cleaned tweets
head(clean_tweets)
[1] " WeNeedFeminlsm MAC s new make up line features men woc and big girls "
[1] " TravelsPhoto What Happens To Your Body One Hour After A Big Mac "データクレンジングミニプロジェクトの最後のステップは、マトリックスに変換してアルゴリズムを適用できるテキストをクリーンアップすることです。に保存されているテキストからclean_tweets ベクトルそれを単語の袋の行列に簡単に変換し、教師なし学習アルゴリズムを適用できます。
ビッグデータ分析では、レポートが非常に重要です。すべての組織は、意思決定プロセスをサポートするために定期的に情報を提供する必要があります。このタスクは通常、SQLおよびETL(抽出、転送、およびロード)の経験を持つデータアナリストによって処理されます。
このタスクを担当するチームは、ビッグデータ分析部門で生成された情報を組織のさまざまな領域に広める責任があります。
次の例は、データの要約の意味を示しています。フォルダに移動しますbda/part1/summarize_data フォルダ内で、 summarize_data.Rprojそれをダブルクリックしてファイルします。次に、summarize_data.R スクリプトを作成してコードを確認し、提示された説明に従ってください。
# Install the following packages by running the following code in R.
pkgs = c('data.table', 'ggplot2', 'nycflights13', 'reshape2')
install.packages(pkgs)ザ・ ggplot2パッケージはデータの視覚化に最適です。ザ・data.table パッケージは、メモリ効率の高い要約を実行するための優れたオプションです。 R。最近のベンチマークは、それがよりもさらに速いことを示していますpandas、同様のタスクに使用されるPythonライブラリ。
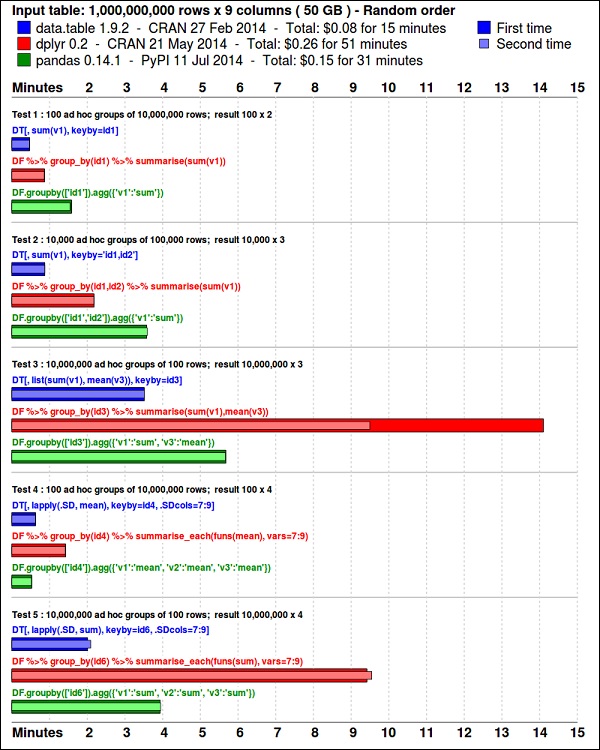
次のコードを使用してデータを確認してください。このコードは、bda/part1/summarize_data/summarize_data.Rproj ファイル。
library(nycflights13)
library(ggplot2)
library(data.table)
library(reshape2)
# Convert the flights data.frame to a data.table object and call it DT
DT <- as.data.table(flights)
# The data has 336776 rows and 16 columns
dim(DT)
# Take a look at the first rows
head(DT)
# year month day dep_time dep_delay arr_time arr_delay carrier
# 1: 2013 1 1 517 2 830 11 UA
# 2: 2013 1 1 533 4 850 20 UA
# 3: 2013 1 1 542 2 923 33 AA
# 4: 2013 1 1 544 -1 1004 -18 B6
# 5: 2013 1 1 554 -6 812 -25 DL
# 6: 2013 1 1 554 -4 740 12 UA
# tailnum flight origin dest air_time distance hour minute
# 1: N14228 1545 EWR IAH 227 1400 5 17
# 2: N24211 1714 LGA IAH 227 1416 5 33
# 3: N619AA 1141 JFK MIA 160 1089 5 42
# 4: N804JB 725 JFK BQN 183 1576 5 44
# 5: N668DN 461 LGA ATL 116 762 5 54
# 6: N39463 1696 EWR ORD 150 719 5 54次のコードには、データの要約の例があります。
### Data Summarization
# Compute the mean arrival delay
DT[, list(mean_arrival_delay = mean(arr_delay, na.rm = TRUE))]
# mean_arrival_delay
# 1: 6.895377
# Now, we compute the same value but for each carrier
mean1 = DT[, list(mean_arrival_delay = mean(arr_delay, na.rm = TRUE)),
by = carrier]
print(mean1)
# carrier mean_arrival_delay
# 1: UA 3.5580111
# 2: AA 0.3642909
# 3: B6 9.4579733
# 4: DL 1.6443409
# 5: EV 15.7964311
# 6: MQ 10.7747334
# 7: US 2.1295951
# 8: WN 9.6491199
# 9: VX 1.7644644
# 10: FL 20.1159055
# 11: AS -9.9308886
# 12: 9E 7.3796692
# 13: F9 21.9207048
# 14: HA -6.9152047
# 15: YV 15.5569853
# 16: OO 11.9310345
# Now let’s compute to means in the same line of code
mean2 = DT[, list(mean_departure_delay = mean(dep_delay, na.rm = TRUE),
mean_arrival_delay = mean(arr_delay, na.rm = TRUE)),
by = carrier]
print(mean2)
# carrier mean_departure_delay mean_arrival_delay
# 1: UA 12.106073 3.5580111
# 2: AA 8.586016 0.3642909
# 3: B6 13.022522 9.4579733
# 4: DL 9.264505 1.6443409
# 5: EV 19.955390 15.7964311
# 6: MQ 10.552041 10.7747334
# 7: US 3.782418 2.1295951
# 8: WN 17.711744 9.6491199
# 9: VX 12.869421 1.7644644
# 10: FL 18.726075 20.1159055
# 11: AS 5.804775 -9.9308886
# 12: 9E 16.725769 7.3796692
# 13: F9 20.215543 21.9207048
# 14: HA 4.900585 -6.9152047
# 15: YV 18.996330 15.5569853
# 16: OO 12.586207 11.9310345
### Create a new variable called gain
# this is the difference between arrival delay and departure delay
DT[, gain:= arr_delay - dep_delay]
# Compute the median gain per carrier
median_gain = DT[, median(gain, na.rm = TRUE), by = carrier]
print(median_gain)Exploratory data analysisは、統計の新しい視点からなるJohn Tuckey(1977)によって開発された概念です。Tuckeyの考えは、従来の統計では、データはグラフィカルに調査されておらず、仮説をテストするために使用されているだけであるというものでした。ツールを開発する最初の試みはスタンフォードで行われ、プロジェクトはprim9と呼ばれていました。このツールは、データを9次元で視覚化することができたため、データの多変量の視点を提供することができました。
最近では、探索的データ分析は必須であり、ビッグデータ分析のライフサイクルに含まれています。洞察を見つけて組織内で効果的に伝達できる能力は、強力なEDA機能によって支えられています。
タッキーのアイデアに基づいて、ベル研究所は S programming language統計を行うためのインタラクティブなインターフェースを提供するため。Sのアイデアは、使いやすい言語で広範なグラフィカル機能を提供することでした。今日の世界では、ビッグデータのコンテキストでは、R それはに基づいています S プログラミング言語は、分析のための最も人気のあるソフトウェアです。
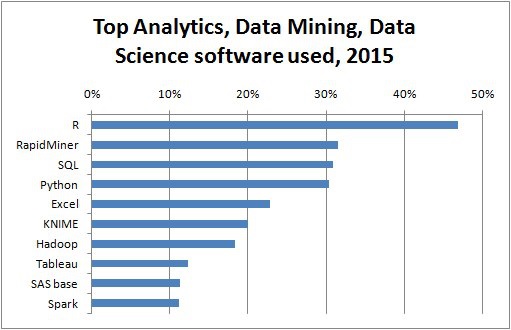
次のプログラムは、探索的データ分析の使用法を示しています。
以下は、探索的データ分析の例です。このコードは、part1/eda/exploratory_data_analysis.R ファイル。
library(nycflights13)
library(ggplot2)
library(data.table)
library(reshape2)
# Using the code from the previous section
# This computes the mean arrival and departure delays by carrier.
DT <- as.data.table(flights)
mean2 = DT[, list(mean_departure_delay = mean(dep_delay, na.rm = TRUE),
mean_arrival_delay = mean(arr_delay, na.rm = TRUE)),
by = carrier]
# In order to plot data in R usign ggplot, it is normally needed to reshape the data
# We want to have the data in long format for plotting with ggplot
dt = melt(mean2, id.vars = ’carrier’)
# Take a look at the first rows
print(head(dt))
# Take a look at the help for ?geom_point and geom_line to find similar examples
# Here we take the carrier code as the x axis
# the value from the dt data.table goes in the y axis
# The variable column represents the color
p = ggplot(dt, aes(x = carrier, y = value, color = variable, group = variable)) +
geom_point() + # Plots points
geom_line() + # Plots lines
theme_bw() + # Uses a white background
labs(list(title = 'Mean arrival and departure delay by carrier',
x = 'Carrier', y = 'Mean delay'))
print(p)
# Save the plot to disk
ggsave('mean_delay_by_carrier.png', p,
width = 10.4, height = 5.07)コードは次のような画像を生成する必要があります-

データを理解するために、データを視覚化すると役立つことがよくあります。通常、ビッグデータアプリケーションでは、関心は単に美しいプロットを作成するのではなく、洞察を見つけることに依存しています。以下は、プロットを使用してデータを理解するためのさまざまなアプローチの例です。
フライトデータの分析を開始するには、数値変数間に相関関係があるかどうかを確認することから始めます。このコードは、bda/part1/data_visualization/data_visualization.R ファイル。
# Install the package corrplot by running
install.packages('corrplot')
# then load the library
library(corrplot)
# Load the following libraries
library(nycflights13)
library(ggplot2)
library(data.table)
library(reshape2)
# We will continue working with the flights data
DT <- as.data.table(flights)
head(DT) # take a look
# We select the numeric variables after inspecting the first rows.
numeric_variables = c('dep_time', 'dep_delay',
'arr_time', 'arr_delay', 'air_time', 'distance')
# Select numeric variables from the DT data.table
dt_num = DT[, numeric_variables, with = FALSE]
# Compute the correlation matrix of dt_num
cor_mat = cor(dt_num, use = "complete.obs")
print(cor_mat)
### Here is the correlation matrix
# dep_time dep_delay arr_time arr_delay air_time distance
# dep_time 1.00000000 0.25961272 0.66250900 0.23230573 -0.01461948 -0.01413373
# dep_delay 0.25961272 1.00000000 0.02942101 0.91480276 -0.02240508 -0.02168090
# arr_time 0.66250900 0.02942101 1.00000000 0.02448214 0.05429603 0.04718917
# arr_delay 0.23230573 0.91480276 0.02448214 1.00000000 -0.03529709 -0.06186776
# air_time -0.01461948 -0.02240508 0.05429603 -0.03529709 1.00000000 0.99064965
# distance -0.01413373 -0.02168090 0.04718917 -0.06186776 0.99064965 1.00000000
# We can display it visually to get a better understanding of the data
corrplot.mixed(cor_mat, lower = "circle", upper = "ellipse")
# save it to disk
png('corrplot.png')
print(corrplot.mixed(cor_mat, lower = "circle", upper = "ellipse"))
dev.off()このコードは、次の相関行列の視覚化を生成します-

プロットを見ると、データセット内のいくつかの変数間に強い相関関係があることがわかります。たとえば、到着遅延と出発遅延には高い相関関係があるようです。楕円は両方の変数間でほぼ直線的な関係を示しているため、これを確認できますが、この結果から因果関係を見つけるのは簡単ではありません。
2つの変数が相関しているため、一方が他方に影響を与えるとは言えません。また、プロットには、飛行時間と距離の間に強い相関関係があることがわかります。これは、距離が長くなると飛行時間が長くなるため、かなり合理的です。
データの単変量分析を行うこともできます。分布を視覚化する簡単で効果的な方法は次のとおりです。box-plots。次のコードは、ggplot2ライブラリを使用して箱ひげ図とトレリスグラフを作成する方法を示しています。このコードは、bda/part1/data_visualization/boxplots.R ファイル。
source('data_visualization.R')
### Analyzing Distributions using box-plots
# The following shows the distance as a function of the carrier
p = ggplot(DT, aes(x = carrier, y = distance, fill = carrier)) + # Define the carrier
in the x axis and distance in the y axis
geom_box-plot() + # Use the box-plot geom
theme_bw() + # Leave a white background - More in line with tufte's
principles than the default
guides(fill = FALSE) + # Remove legend
labs(list(title = 'Distance as a function of carrier', # Add labels
x = 'Carrier', y = 'Distance'))
p
# Save to disk
png(‘boxplot_carrier.png’)
print(p)
dev.off()
# Let's add now another variable, the month of each flight
# We will be using facet_wrap for this
p = ggplot(DT, aes(carrier, distance, fill = carrier)) +
geom_box-plot() +
theme_bw() +
guides(fill = FALSE) +
facet_wrap(~month) + # This creates the trellis plot with the by month variable
labs(list(title = 'Distance as a function of carrier by month',
x = 'Carrier', y = 'Distance'))
p
# The plot shows there aren't clear differences between distance in different months
# Save to disk
png('boxplot_carrier_by_month.png')
print(p)
dev.off()このセクションでは、ユーザーにRプログラミング言語を紹介します。Rはクランのウェブサイトからダウンロードできます。Windowsユーザーの場合は、するのに便利ですrtoolsインストールとrstudio IDEを。
背後にある一般的な概念 R C、C ++、Fortranなどのコンパイル言語で開発された他のソフトウェアへのインターフェイスとして機能し、データを分析するためのインタラクティブなツールをユーザーに提供します。
ブックのzipファイルのフォルダーに移動します bda/part2/R_introduction を開きます R_introduction.Rprojファイル。これにより、RStudioセッションが開きます。次に、01_vectors.Rファイルを開きます。スクリプトを1行ずつ実行し、コード内のコメントに従います。学習するためのもう1つの便利なオプションは、コードを入力することです。これは、R構文に慣れるのに役立ちます。Rではコメントは#記号で書かれています。
ブックでRコードを実行した結果を表示するために、コードが評価された後、Rが返す結果にコメントが付けられます。このようにして、本にコードをコピーして貼り付け、Rでコードのセクションを直接試すことができます。
# Create a vector of numbers
numbers = c(1, 2, 3, 4, 5)
print(numbers)
# [1] 1 2 3 4 5
# Create a vector of letters
ltrs = c('a', 'b', 'c', 'd', 'e')
# [1] "a" "b" "c" "d" "e"
# Concatenate both
mixed_vec = c(numbers, ltrs)
print(mixed_vec)
# [1] "1" "2" "3" "4" "5" "a" "b" "c" "d" "e"前のコードで何が起こったのかを分析してみましょう。数字と文字でベクトルを作成できることがわかります。事前にどのタイプのデータ型が必要かをRに伝える必要はありませんでした。最後に、数字と文字の両方を含むベクトルを作成することができました。ベクトルmixed_vecは数値を文字に強制変換しました。これは、値が引用符で囲まれてどのように出力されるかを視覚化することで確認できます。
次のコードは、関数クラスによって返されるさまざまなベクトルのデータ型を示しています。クラス関数を使用してオブジェクトを「問い合わせ」、クラスが何であるかを尋ねるのが一般的です。
### Evaluate the data types using class
### One dimensional objects
# Integer vector
num = 1:10
class(num)
# [1] "integer"
# Numeric vector, it has a float, 10.5
num = c(1:10, 10.5)
class(num)
# [1] "numeric"
# Character vector
ltrs = letters[1:10]
class(ltrs)
# [1] "character"
# Factor vector
fac = as.factor(ltrs)
class(fac)
# [1] "factor"Rは2次元オブジェクトもサポートします。次のコードには、Rで使用される2つの最も一般的なデータ構造の例があります。matrixとdata.frameです。
# Matrix
M = matrix(1:12, ncol = 4)
# [,1] [,2] [,3] [,4]
# [1,] 1 4 7 10
# [2,] 2 5 8 11
# [3,] 3 6 9 12
lM = matrix(letters[1:12], ncol = 4)
# [,1] [,2] [,3] [,4]
# [1,] "a" "d" "g" "j"
# [2,] "b" "e" "h" "k"
# [3,] "c" "f" "i" "l"
# Coerces the numbers to character
# cbind concatenates two matrices (or vectors) in one matrix
cbind(M, lM)
# [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
# [1,] "1" "4" "7" "10" "a" "d" "g" "j"
# [2,] "2" "5" "8" "11" "b" "e" "h" "k"
# [3,] "3" "6" "9" "12" "c" "f" "i" "l"
class(M)
# [1] "matrix"
class(lM)
# [1] "matrix"
# data.frame
# One of the main objects of R, handles different data types in the same object.
# It is possible to have numeric, character and factor vectors in the same data.frame
df = data.frame(n = 1:5, l = letters[1:5])
df
# n l
# 1 1 a
# 2 2 b
# 3 3 c
# 4 4 d
# 5 5 e前の例で示したように、同じオブジェクトで異なるデータ型を使用することが可能です。一般に、これはデータベースでのデータの表示方法です。データのAPI部分は、テキストまたは文字ベクトル、およびその他の数値です。Inは、割り当てる統計データ型を決定し、それに正しいRデータ型を使用するアナリストの仕事です。統計では、通常、変数は次のタイプであると見なされます-
- Numeric
- 名目またはカテゴリ
- Ordinal
Rでは、ベクトルは次のクラスになります。
- 数値-整数
- Factor
- オーダードファクター
Rは、変数の統計タイプごとにデータ型を提供します。ただし、順序付き因子はめったに使用されませんが、関数因子によって作成することも、順序付けすることもできます。
次のセクションでは、インデックス作成の概念について説明します。これは非常に一般的な操作であり、オブジェクトのセクションを選択してそれらに変換する問題を扱います。
# Let's create a data.frame
df = data.frame(numbers = 1:26, letters)
head(df)
# numbers letters
# 1 1 a
# 2 2 b
# 3 3 c
# 4 4 d
# 5 5 e
# 6 6 f
# str gives the structure of a data.frame, it’s a good summary to inspect an object
str(df)
# 'data.frame': 26 obs. of 2 variables:
# $ numbers: int 1 2 3 4 5 6 7 8 9 10 ... # $ letters: Factor w/ 26 levels "a","b","c","d",..: 1 2 3 4 5 6 7 8 9 10 ...
# The latter shows the letters character vector was coerced as a factor.
# This can be explained by the stringsAsFactors = TRUE argumnet in data.frame
# read ?data.frame for more information
class(df)
# [1] "data.frame"
### Indexing
# Get the first row
df[1, ]
# numbers letters
# 1 1 a
# Used for programming normally - returns the output as a list
df[1, , drop = TRUE]
# $numbers # [1] 1 # # $letters
# [1] a
# Levels: a b c d e f g h i j k l m n o p q r s t u v w x y z
# Get several rows of the data.frame
df[5:7, ]
# numbers letters
# 5 5 e
# 6 6 f
# 7 7 g
### Add one column that mixes the numeric column with the factor column
df$mixed = paste(df$numbers, df$letters, sep = ’’) str(df) # 'data.frame': 26 obs. of 3 variables: # $ numbers: int 1 2 3 4 5 6 7 8 9 10 ...
# $ letters: Factor w/ 26 levels "a","b","c","d",..: 1 2 3 4 5 6 7 8 9 10 ... # $ mixed : chr "1a" "2b" "3c" "4d" ...
### Get columns
# Get the first column
df[, 1]
# It returns a one dimensional vector with that column
# Get two columns
df2 = df[, 1:2]
head(df2)
# numbers letters
# 1 1 a
# 2 2 b
# 3 3 c
# 4 4 d
# 5 5 e
# 6 6 f
# Get the first and third columns
df3 = df[, c(1, 3)]
df3[1:3, ]
# numbers mixed
# 1 1 1a
# 2 2 2b
# 3 3 3c
### Index columns from their names
names(df)
# [1] "numbers" "letters" "mixed"
# This is the best practice in programming, as many times indeces change, but
variable names don’t
# We create a variable with the names we want to subset
keep_vars = c("numbers", "mixed")
df4 = df[, keep_vars]
head(df4)
# numbers mixed
# 1 1 1a
# 2 2 2b
# 3 3 3c
# 4 4 4d
# 5 5 5e
# 6 6 6f
### subset rows and columns
# Keep the first five rows
df5 = df[1:5, keep_vars]
df5
# numbers mixed
# 1 1 1a
# 2 2 2b
# 3 3 3c
# 4 4 4d
# 5 5 5e
# subset rows using a logical condition
df6 = df[df$numbers < 10, keep_vars]
df6
# numbers mixed
# 1 1 1a
# 2 2 2b
# 3 3 3c
# 4 4 4d
# 5 5 5e
# 6 6 6f
# 7 7 7g
# 8 8 8h
# 9 9 9iSQLは構造化照会言語の略です。これは、従来のデータウェアハウスやビッグデータテクノロジーのデータベースからデータを抽出するために最も広く使用されている言語の1つです。SQLの基本を示すために、例を使用します。言語自体に焦点を合わせるために、R内でSQLを使用します。SQLコードの記述に関しては、これはデータベースで行われるのとまったく同じです。
SQLの中核は、SELECT、FROM、WHEREの3つのステートメントです。次の例では、SQLの最も一般的なユースケースを利用しています。フォルダに移動しますbda/part2/SQL_introduction を開きます SQL_introduction.Rprojファイル。次に、01_select.Rスクリプトを開きます。RでSQLコードを作成するには、をインストールする必要があります。sqldf 次のコードに示されているパッケージ。
# Install the sqldf package
install.packages('sqldf')
# load the library
library('sqldf')
library(nycflights13)
# We will be working with the fligths dataset in order to introduce SQL
# Let’s take a look at the table
str(flights)
# Classes 'tbl_d', 'tbl' and 'data.frame': 336776 obs. of 16 variables:
# $ year : int 2013 2013 2013 2013 2013 2013 2013 2013 2013 2013 ...
# $ month : int 1 1 1 1 1 1 1 1 1 1 ... # $ day : int 1 1 1 1 1 1 1 1 1 1 ...
# $ dep_time : int 517 533 542 544 554 554 555 557 557 558 ... # $ dep_delay: num 2 4 2 -1 -6 -4 -5 -3 -3 -2 ...
# $ arr_time : int 830 850 923 1004 812 740 913 709 838 753 ... # $ arr_delay: num 11 20 33 -18 -25 12 19 -14 -8 8 ...
# $ carrier : chr "UA" "UA" "AA" "B6" ... # $ tailnum : chr "N14228" "N24211" "N619AA" "N804JB" ...
# $ flight : int 1545 1714 1141 725 461 1696 507 5708 79 301 ... # $ origin : chr "EWR" "LGA" "JFK" "JFK" ...
# $ dest : chr "IAH" "IAH" "MIA" "BQN" ... # $ air_time : num 227 227 160 183 116 150 158 53 140 138 ...
# $ distance : num 1400 1416 1089 1576 762 ... # $ hour : num 5 5 5 5 5 5 5 5 5 5 ...
# $ minute : num 17 33 42 44 54 54 55 57 57 58 ...selectステートメントは、テーブルから列を取得し、それらに対して計算を行うために使用されます。最も単純なSELECTステートメントは次のように示されています。ej1。に示すように、新しい変数を作成することもできます。ej2。
### SELECT statement
ej1 = sqldf("
SELECT
dep_time
,dep_delay
,arr_time
,carrier
,tailnum
FROM
flights
")
head(ej1)
# dep_time dep_delay arr_time carrier tailnum
# 1 517 2 830 UA N14228
# 2 533 4 850 UA N24211
# 3 542 2 923 AA N619AA
# 4 544 -1 1004 B6 N804JB
# 5 554 -6 812 DL N668DN
# 6 554 -4 740 UA N39463
# In R we can use SQL with the sqldf function. It works exactly the same as in
a database
# The data.frame (in this case flights) represents the table we are querying
and goes in the FROM statement
# We can also compute new variables in the select statement using the syntax:
# old_variables as new_variable
ej2 = sqldf("
SELECT
arr_delay - dep_delay as gain,
carrier
FROM
flights
")
ej2[1:5, ]
# gain carrier
# 1 9 UA
# 2 16 UA
# 3 31 AA
# 4 -17 B6
# 5 -19 DLSQLで最も一般的に使用される機能の1つは、groupbyステートメントです。これにより、別の変数のさまざまなグループの数値を計算できます。スクリプト02_group_by.Rを開きます。
### GROUP BY
# Computing the average
ej3 = sqldf("
SELECT
avg(arr_delay) as mean_arr_delay,
avg(dep_delay) as mean_dep_delay,
carrier
FROM
flights
GROUP BY
carrier
")
# mean_arr_delay mean_dep_delay carrier
# 1 7.3796692 16.725769 9E
# 2 0.3642909 8.586016 AA
# 3 -9.9308886 5.804775 AS
# 4 9.4579733 13.022522 B6
# 5 1.6443409 9.264505 DL
# 6 15.7964311 19.955390 EV
# 7 21.9207048 20.215543 F9
# 8 20.1159055 18.726075 FL
# 9 -6.9152047 4.900585 HA
# 10 10.7747334 10.552041 MQ
# 11 11.9310345 12.586207 OO
# 12 3.5580111 12.106073 UA
# 13 2.1295951 3.782418 US
# 14 1.7644644 12.869421 VX
# 15 9.6491199 17.711744 WN
# 16 15.5569853 18.996330 YV
# Other aggregations
ej4 = sqldf("
SELECT
avg(arr_delay) as mean_arr_delay,
min(dep_delay) as min_dep_delay,
max(dep_delay) as max_dep_delay,
carrier
FROM
flights
GROUP BY
carrier
")
# We can compute the minimun, mean, and maximum values of a numeric value
ej4
# mean_arr_delay min_dep_delay max_dep_delay carrier
# 1 7.3796692 -24 747 9E
# 2 0.3642909 -24 1014 AA
# 3 -9.9308886 -21 225 AS
# 4 9.4579733 -43 502 B6
# 5 1.6443409 -33 960 DL
# 6 15.7964311 -32 548 EV
# 7 21.9207048 -27 853 F9
# 8 20.1159055 -22 602 FL
# 9 -6.9152047 -16 1301 HA
# 10 10.7747334 -26 1137 MQ
# 11 11.9310345 -14 154 OO
# 12 3.5580111 -20 483 UA
# 13 2.1295951 -19 500 US
# 14 1.7644644 -20 653 VX
# 15 9.6491199 -13 471 WN
# 16 15.5569853 -16 387 YV
### We could be also interested in knowing how many observations each carrier has
ej5 = sqldf("
SELECT
carrier, count(*) as count
FROM
flights
GROUP BY
carrier
")
ej5
# carrier count
# 1 9E 18460
# 2 AA 32729
# 3 AS 714
# 4 B6 54635
# 5 DL 48110
# 6 EV 54173
# 7 F9 685
# 8 FL 3260
# 9 HA 342
# 10 MQ 26397
# 11 OO 32
# 12 UA 58665
# 13 US 20536
# 14 VX 5162
# 15 WN 12275
# 16 YV 601SQLの最も便利な機能は結合です。結合とは、1つの列を使用してテーブルAとテーブルBを1つのテーブルに結合し、両方のテーブルの値を一致させることを意味します。結合にはさまざまなタイプがあり、実際には、開始するには、これらが最も有用なものになります。内部結合と左外部結合です。
# Let’s create two tables: A and B to demonstrate joins.
A = data.frame(c1 = 1:4, c2 = letters[1:4])
B = data.frame(c1 = c(2,4,5,6), c2 = letters[c(2:5)])
A
# c1 c2
# 1 a
# 2 b
# 3 c
# 4 d
B
# c1 c2
# 2 b
# 4 c
# 5 d
# 6 e
### INNER JOIN
# This means to match the observations of the column we would join the tables by.
inner = sqldf("
SELECT
A.c1, B.c2
FROM
A INNER JOIN B
ON A.c1 = B.c1
")
# Only the rows that match c1 in both A and B are returned
inner
# c1 c2
# 2 b
# 4 c
### LEFT OUTER JOIN
# the left outer join, sometimes just called left join will return the
# first all the values of the column used from the A table
left = sqldf("
SELECT
A.c1, B.c2
FROM
A LEFT OUTER JOIN B
ON A.c1 = B.c1
")
# Only the rows that match c1 in both A and B are returned
left
# c1 c2
# 1 <NA>
# 2 b
# 3 <NA>
# 4 cデータを分析するための最初のアプローチは、データを視覚的に分析することです。これを行う目的は、通常、変数と変数の単変量記述の間の関係を見つけることです。これらの戦略は次のように分けることができます-
- 単変量分析
- 多変量解析
単変量グラフィカルメソッド
Univariateは統計用語です。実際には、残りのデータから独立して変数を分析したいということです。これを効率的に行うことができるプロットは次のとおりです。
箱ひげ図
箱ひげ図は通常、分布を比較するために使用されます。これは、分布間に違いがあるかどうかを視覚的に検査するための優れた方法です。カットごとにダイヤモンドの価格に違いがあるかどうかを確認できます。
# We will be using the ggplot2 library for plotting
library(ggplot2)
data("diamonds")
# We will be using the diamonds dataset to analyze distributions of numeric variables
head(diamonds)
# carat cut color clarity depth table price x y z
# 1 0.23 Ideal E SI2 61.5 55 326 3.95 3.98 2.43
# 2 0.21 Premium E SI1 59.8 61 326 3.89 3.84 2.31
# 3 0.23 Good E VS1 56.9 65 327 4.05 4.07 2.31
# 4 0.29 Premium I VS2 62.4 58 334 4.20 4.23 2.63
# 5 0.31 Good J SI2 63.3 58 335 4.34 4.35 2.75
# 6 0.24 Very Good J VVS2 62.8 57 336 3.94 3.96 2.48
### Box-Plots
p = ggplot(diamonds, aes(x = cut, y = price, fill = cut)) +
geom_box-plot() +
theme_bw()
print(p)プロットでは、カットの種類によってダイヤモンドの価格の分布に違いがあることがわかります。

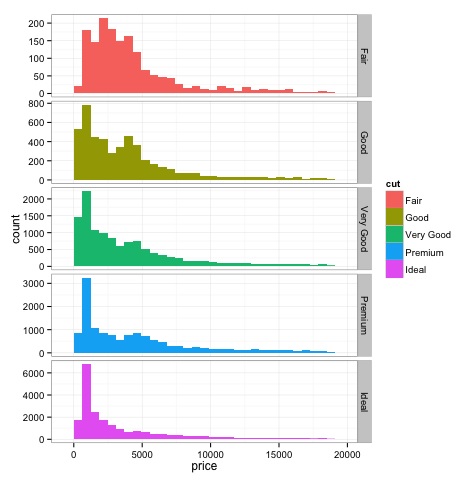
ヒストグラム
source('01_box_plots.R')
# We can plot histograms for each level of the cut factor variable using
facet_grid
p = ggplot(diamonds, aes(x = price, fill = cut)) +
geom_histogram() +
facet_grid(cut ~ .) +
theme_bw()
p
# the previous plot doesn’t allow to visuallize correctly the data because of
the differences in scale
# we can turn this off using the scales argument of facet_grid
p = ggplot(diamonds, aes(x = price, fill = cut)) +
geom_histogram() +
facet_grid(cut ~ ., scales = 'free') +
theme_bw()
p
png('02_histogram_diamonds_cut.png')
print(p)
dev.off()上記のコードの出力は次のようになります-
多変量グラフィカルメソッド
探索的データ分析における多変量グラフィカル手法には、さまざまな変数間の関係を見つけることを目的としています。これを実現するには、一般的に使用される2つの方法があります。数値変数の相関行列をプロットする方法と、単に散布図の行列として生データをプロットする方法です。
これを示すために、diamondsデータセットを使用します。コードに従うには、スクリプトを開きますbda/part2/charts/03_multivariate_analysis.R。
library(ggplot2)
data(diamonds)
# Correlation matrix plots
keep_vars = c('carat', 'depth', 'price', 'table')
df = diamonds[, keep_vars]
# compute the correlation matrix
M_cor = cor(df)
# carat depth price table
# carat 1.00000000 0.02822431 0.9215913 0.1816175
# depth 0.02822431 1.00000000 -0.0106474 -0.2957785
# price 0.92159130 -0.01064740 1.0000000 0.1271339
# table 0.18161755 -0.29577852 0.1271339 1.0000000
# plots
heat-map(M_cor)コードは次の出力を生成します-

これは要約であり、価格とキャレットの間には強い相関関係があり、他の変数の間にはあまり相関関係がないことを示しています。
相関行列は、変数が多数ある場合に役立ちます。その場合、生データのプロットは実用的ではありません。前述のように、生データを表示することも可能です-
library(GGally)
ggpairs(df)ヒートマップに表示された結果が確認されていることがプロットでわかります。価格とカラットの変数の間には0.922の相関関係があります。
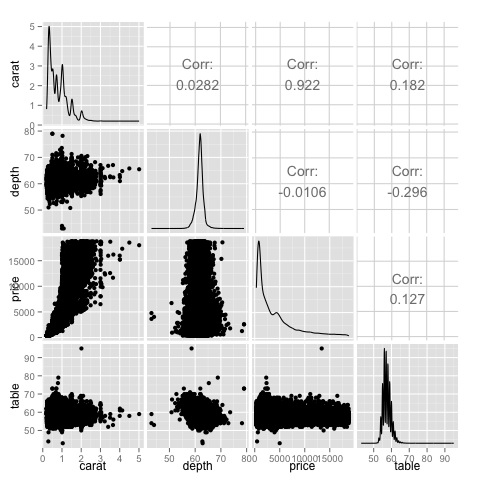
この関係は、散布図行列の(3、1)インデックスにある価格カラット散布図で視覚化できます。
データサイエンティストがデータを効果的に分析できるようにするさまざまなツールがあります。通常、データ分析のエンジニアリングの側面はデータベースに焦点を当て、データサイエンティストはデータ製品を実装できるツールに焦点を当てています。次のセクションでは、データサイエンティストが実際に最も頻繁に使用する統計パッケージに焦点を当てて、さまざまなツールの利点について説明します。
Rプログラミング言語
Rは、統計分析に重点を置いたオープンソースのプログラミング言語です。統計機能の点で、SAS、SPSSなどの商用ツールと競合します。これは、C、C ++、Fortranなどの他のプログラミング言語へのインターフェースであると考えられています。
Rのもう1つの利点は、利用可能なオープンソースライブラリが多数あることです。CRANには、無料でダウンロードできる6000を超えるパッケージがあります。Github さまざまなRパッケージが利用可能です。
パフォーマンスの観点から、Rは集中的な操作では低速です。使用可能なライブラリが大量にあるため、コードの低速セクションはコンパイルされた言語で記述されています。ただし、深いforループを記述する必要のある操作を実行する場合は、Rが最適な代替手段ではありません。データ分析の目的で、次のような素晴らしいライブラリがありますdata.table, glmnet, ranger, xgboost, ggplot2, caret これにより、Rをより高速なプログラミング言語へのインターフェースとして使用できます。
データ分析のためのPython
Pythonは汎用プログラミング言語であり、次のようなデータ分析専用のライブラリが多数含まれています。 pandas, scikit-learn, theano, numpy そして scipy。
Rで利用できることのほとんどはPythonでも実行できますが、Rの方が使いやすいことがわかりました。大規模なデータセットを使用している場合は、通常、RよりもPythonの方が適しています。Pythonを非常に効果的に使用して、データを1行ずつクリーンアップおよび処理できます。これはRから可能ですが、スクリプトタスクではPythonほど効率的ではありません。
機械学習の場合、 scikit-learnは、中規模のデータセットを問題なく処理できる大量のアルゴリズムを利用できる優れた環境です。Rの同等のライブラリ(キャレット)と比較して、scikit-learn よりクリーンで一貫性のあるAPIを備えています。
ジュリア
Juliaは、テクニカルコンピューティング用の高レベルで高性能な動的プログラミング言語です。その構文はRまたはPythonと非常に似ているため、すでにRまたはPythonを使用している場合は、Juliaで同じコードを記述するのは非常に簡単です。この言語は非常に新しく、ここ数年で大幅に成長したため、現時点では間違いなくオプションです。
ニューラルネットワークなど、計算量の多いアルゴリズムのプロトタイピングにはJuliaをお勧めします。それは研究のための素晴らしいツールです。実稼働環境でモデルを実装するという点では、おそらくPythonの方が優れた選択肢があります。ただし、R、Python、Juliaでモデルを実装するエンジニアリングを行うWebサービスがあるため、これはそれほど問題になりません。
SAS
SASは、ビジネスインテリジェンスに現在も使用されている商用言語です。これには、ユーザーがさまざまなアプリケーションをプログラムできるようにする基本言語があります。専門家でないユーザーがプログラミングを必要とせずにニューラルネットワークライブラリなどの複雑なツールを使用できるようにする、かなりの数の商用製品が含まれています。
商用ツールの明らかな欠点を超えて、SASは大規模なデータセットにうまく対応できません。中規模のデータセットでもSASに問題があり、サーバーがクラッシュします。小さなデータセットを使用していて、ユーザーがデータサイエンティストの専門家でない場合にのみ、SASをお勧めします。上級ユーザーの場合、RとPythonはより生産的な環境を提供します。
SPSS
SPSSは現在、統計分析用のIBMの製品です。これは主に調査データの分析に使用され、プログラミングできないユーザーにとっては適切な代替手段です。SASと同じくらい簡単に使用できますが、モデルの実装に関しては、モデルにスコアを付けるためのSQLコードを提供するので簡単です。このコードは通常効率的ではありませんが、SASが各データベースのモデルを個別にスコアリングする製品を販売しているのに対し、これは始まりです。小さなデータや経験の浅いチームにとって、SPSSはSASと同じくらい優れたオプションです。
ただし、ソフトウェアはかなり制限されており、経験豊富なユーザーはRまたはPythonを使用すると生産性が大幅に向上します。
Matlab、Octave
Matlabやそのオープンソースバージョン(Octave)などの他のツールも利用できます。これらのツールは主に研究に使用されます。機能に関しては、RまたはPythonはMatlabまたはOctaveで利用可能なすべてのことを実行できます。製品が提供するサポートに関心がある場合にのみ、製品のライセンスを購入するのが理にかなっています。
データを分析するとき、統計的アプローチを持つことが可能です。基本的な分析を実行するために必要な基本的なツールは次のとおりです。
- 相関分析
- 分散分析
- 仮説検定
大規模なデータセットを操作する場合、相関分析を除いて、これらの方法は計算量が多くないため、問題は発生しません。この場合、サンプルを取得することは常に可能であり、結果は堅牢である必要があります。
相関分析
相関分析は、数値変数間の線形関係を見つけようとします。これは、さまざまな状況で役立ちます。一般的な使用法の1つは探索的データ分析であり、本のセクション16.0.2に、このアプローチの基本的な例があります。まず、前述の例で使用されている相関メトリックは、Pearson coefficient。ただし、外れ値の影響を受けない別の興味深い相関メトリックがあります。このメトリックは、スピアマン相関と呼ばれます。
ザ・ spearman correlation メトリックは、ピアソン法よりも外れ値の存在に対してロバストであり、データが正規分布していない場合に数値変数間の線形関係をより正確に推定できます。
library(ggplot2)
# Select variables that are interesting to compare pearson and spearman
correlation methods.
x = diamonds[, c('x', 'y', 'z', 'price')]
# From the histograms we can expect differences in the correlations of both
metrics.
# In this case as the variables are clearly not normally distributed, the
spearman correlation
# is a better estimate of the linear relation among numeric variables.
par(mfrow = c(2,2))
colnm = names(x)
for(i in 1:4) {
hist(x[[i]], col = 'deepskyblue3', main = sprintf('Histogram of %s', colnm[i]))
}
par(mfrow = c(1,1))次の図のヒストグラムから、両方のメトリックの相関関係の違いが予想されます。この場合、変数は明らかに正規分布していないため、スピアマン相関は数値変数間の線形関係のより良い推定値です。
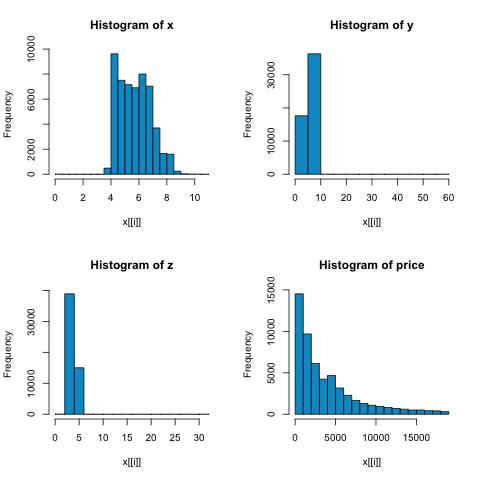
Rの相関を計算するには、ファイルを開きます bda/part2/statistical_methods/correlation/correlation.R このコードセクションがあります。
## Correlation Matrix - Pearson and spearman
cor_pearson <- cor(x, method = 'pearson')
cor_spearman <- cor(x, method = 'spearman')
### Pearson Correlation
print(cor_pearson)
# x y z price
# x 1.0000000 0.9747015 0.9707718 0.8844352
# y 0.9747015 1.0000000 0.9520057 0.8654209
# z 0.9707718 0.9520057 1.0000000 0.8612494
# price 0.8844352 0.8654209 0.8612494 1.0000000
### Spearman Correlation
print(cor_spearman)
# x y z price
# x 1.0000000 0.9978949 0.9873553 0.9631961
# y 0.9978949 1.0000000 0.9870675 0.9627188
# z 0.9873553 0.9870675 1.0000000 0.9572323
# price 0.9631961 0.9627188 0.9572323 1.0000000カイ二乗検定
カイ二乗検定を使用すると、2つの確率変数が独立しているかどうかを検定できます。これは、各変数の確率分布が他の変数に影響を与えないことを意味します。Rでテストを評価するには、最初に分割表を作成してから、その表を分割表に渡す必要があります。chisq.test R 関数。
たとえば、変数の間に関連があるかどうかを確認しましょう:ダイヤモンドデータセットからのカットとカラー。テストは正式には次のように定義されます-
- H0:可変カットとダイアモンドは独立しています
- H1:可変カットとダイヤモンドは独立していません
これらの2つの変数の間には名前で関係があると想定しますが、テストでは、この結果がどれほど重要であるかを示す客観的な「ルール」を与えることができます。
次のコードスニペットでは、テストのp値が2.2e-16であることがわかりました。これは、実際にはほぼゼロです。次に、テストを実行した後、Monte Carlo simulation、p値は0.0004998であり、しきい値0.05よりもかなり低いことがわかりました。この結果は、帰無仮説(H0)を棄却することを意味するため、変数はcut そして color 独立していません。
library(ggplot2)
# Use the table function to compute the contingency table
tbl = table(diamonds$cut, diamonds$color)
tbl
# D E F G H I J
# Fair 163 224 312 314 303 175 119
# Good 662 933 909 871 702 522 307
# Very Good 1513 2400 2164 2299 1824 1204 678
# Premium 1603 2337 2331 2924 2360 1428 808
# Ideal 2834 3903 3826 4884 3115 2093 896
# In order to run the test we just use the chisq.test function.
chisq.test(tbl)
# Pearson’s Chi-squared test
# data: tbl
# X-squared = 310.32, df = 24, p-value < 2.2e-16
# It is also possible to compute the p-values using a monte-carlo simulation
# It's needed to add the simulate.p.value = TRUE flag and the amount of
simulations
chisq.test(tbl, simulate.p.value = TRUE, B = 2000)
# Pearson’s Chi-squared test with simulated p-value (based on 2000 replicates)
# data: tbl
# X-squared = 310.32, df = NA, p-value = 0.0004998T検定
のアイデア t-test名義変数の異なるグループ間で数値変数の分布に違いがあるかどうかを評価することです。これを実証するために、因子変数カットの公正レベルと理想レベルのレベルを選択し、次にこれら2つのグループ間で数値変数の値を比較します。
data = diamonds[diamonds$cut %in% c('Fair', 'Ideal'), ]
data$cut = droplevels.factor(data$cut) # Drop levels that aren’t used from the
cut variable
df1 = data[, c('cut', 'price')]
# We can see the price means are different for each group
tapply(df1$price, df1$cut, mean)
# Fair Ideal
# 4358.758 3457.542t検定は、Rで実装されます。 t.test関数。t.testの数式インターフェイスは、これを使用する最も簡単な方法です。数値変数はグループ変数によって説明されるという考え方です。
例えば: t.test(numeric_variable ~ group_variable, data = data)。前の例では、numeric_variable です price そしてその group_variable です cut。
統計的な観点から、2つのグループ間で数値変数の分布に違いがあるかどうかをテストしています。正式には、仮説検定は、帰無仮説(H0)と対立仮説(H1)で記述されます。
H0:公正グループと理想グループの間で価格変数の分布に違いはありません
H1公正グループと理想グループの間で価格変数の分布に違いがあります
以下のコードを使用して、Rで以下を実装できます。
t.test(price ~ cut, data = data)
# Welch Two Sample t-test
#
# data: price by cut
# t = 9.7484, df = 1894.8, p-value < 2.2e-16
# alternative hypothesis: true difference in means is not equal to 0
# 95 percent confidence interval:
# 719.9065 1082.5251
# sample estimates:
# mean in group Fair mean in group Ideal
# 4358.758 3457.542
# Another way to validate the previous results is to just plot the
distributions using a box-plot
plot(price ~ cut, data = data, ylim = c(0,12000),
col = 'deepskyblue3')p値が0.05未満であるかどうかを確認することで、テスト結果を分析できます。この場合、対立仮説を維持します。これは、カットファクターの2つのレベル間で価格の違いが見つかったことを意味します。レベルの名前から、この結果を期待していましたが、Failグループの平均価格がIdealグループよりも高くなるとは予想していませんでした。これは、各要因の平均を比較することでわかります。
ザ・ plotコマンドは、価格とカット変数の関係を示すグラフを生成します。これは箱ひげ図です。このプロットについてはセクション16.0.1で説明しましたが、基本的には、分析している2つのレベルのカットの価格変数の分布を示しています。
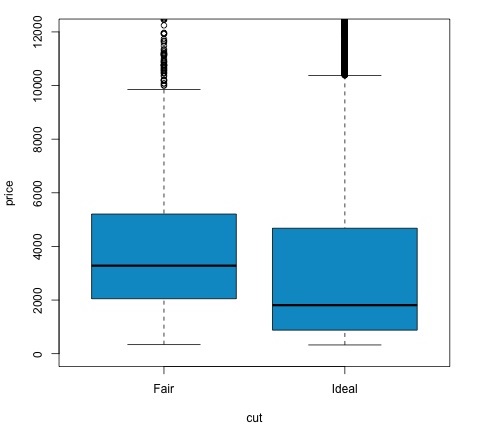
分散分析
分散分析(ANOVA)は、各グループの平均と分散を比較することによってグループ分布間の差異を分析するために使用される統計モデルであり、モデルはロナルドフィッシャーによって開発されました。ANOVAは、複数のグループの平均が等しいかどうかの統計的検定を提供するため、t検定を3つ以上のグループに一般化します。
ANOVAは、統計的有意性について3つ以上のグループを比較するのに役立ちます。これは、複数の2標本t検定を実行すると、統計的なタイプIエラーが発生する可能性が高くなるためです。
数学的説明を提供するという点で、テストを理解するために以下が必要です。
x ij = x +(x i − x)+(x ij − x)
これは次のモデルにつながります-
X IJ =μ+α I +∈ IJ
μは総平均で、どこで、α iは、 i番目のグループの平均値です。誤差項∈ ijは正規分布からIIDされているものとします。テストの帰無仮説は次のとおりです。
α 1 =α 2 = ... =α K
検定統計量の計算に関しては、2つの値を計算する必要があります-
- グループ間の差の二乗和-
$$SSD_B = \sum_{i}^{k} \sum_{j}^{n}(\bar{x_{\bar{i}}} - \bar{x})^2$$
- グループ内の平方和
$$SSD_W = \sum_{i}^{k} \sum_{j}^{n}(\bar{x_{\bar{ij}}} - \bar{x_{\bar{i}}})^2$$
SSDここでBは、 K-1の自由度を有し、SSD Wは、 N-Kの自由度を有しています。次に、各メトリックの平均二乗差を定義できます。
MS B = SSD B /(k-1)
MS w = SSD w /(N-k)
最後に、ANOVAの検定統計量は、上記の2つの量の比率として定義されます。
F = MS B / MS w
これは、k-1およびN-kの自由度を持つF分布に従います。帰無仮説が真の場合、Fは1に近い可能性があります。そうでない場合、グループ間の平均二乗MSBが大きくなる可能性があり、その結果、F値が大きくなります。
基本的に、ANOVAは、全分散の2つの原因を調べ、どちらの部分がより寄与しているかを確認します。これが、グループ平均を比較することを目的としていますが、分散分析と呼ばれる理由です。
統計の計算に関しては、実際にはRで行うのはかなり簡単です。次の例は、それがどのように行われるかを示し、結果をプロットします。
library(ggplot2)
# We will be using the mtcars dataset
head(mtcars)
# mpg cyl disp hp drat wt qsec vs am gear carb
# Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
# Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
# Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
# Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
# Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
# Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1
# Let's see if there are differences between the groups of cyl in the mpg variable.
data = mtcars[, c('mpg', 'cyl')]
fit = lm(mpg ~ cyl, data = mtcars)
anova(fit)
# Analysis of Variance Table
# Response: mpg
# Df Sum Sq Mean Sq F value Pr(>F)
# cyl 1 817.71 817.71 79.561 6.113e-10 ***
# Residuals 30 308.33 10.28
# Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 .
# Plot the distribution
plot(mpg ~ as.factor(cyl), data = mtcars, col = 'deepskyblue3')コードは次の出力を生成します-

この例で取得したp値は0.05よりも大幅に小さいため、Rはこれを示す記号「***」を返します。これは、帰無仮説を棄却し、mpg平均の異なるグループ間での違いを見つけることを意味します。cyl 変数。
機械学習は、パターン認識、コンピュータービジョン、音声認識、テキスト分析などのタスクを扱うコンピューターサイエンスのサブフィールドであり、統計や数理最適化と強いつながりがあります。アプリケーションには、検索エンジン、スパムフィルタリング、光学式文字認識(OCR)などの開発が含まれます。データマイニング、パターン認識、統計学習の分野の境界は明確ではなく、基本的にすべてが同様の問題を参照しています。
機械学習は2つのタイプのタスクに分けることができます-
- 教師あり学習
- 教師なし学習
教師あり学習
教師あり学習とは、行列Xとして定義された入力データがあり、応答yの予測に関心があるタイプの問題を指します。ここで、X = {X 1、X 2、···、Xのnは}有するN予測子を2つの値有する{C、Y =を1 C、2 }。
アプリケーションの例は、人口統計学的機能を予測子として使用して、Webユーザーが広告をクリックする確率を予測することです。これは、クリック率(CTR)を予測するためによく呼び出されます。次に、y = {クリック、クリックしない}であり、予測子は、使用可能なIPアドレス、サイトにアクセスした日、ユーザーの都市、国など、利用可能な機能である可能性があります。
教師なし学習
教師なし学習は、学習するクラスがなくても、互いに類似しているグループを見つけるという問題を扱います。予測子からマッピングを学習して、各グループで同様のインスタンスを共有し、互いに異なるグループを見つけるタスクには、いくつかのアプローチがあります。
教師なし学習のアプリケーションの例は、顧客のセグメンテーションです。たとえば、電気通信業界では、一般的なタスクは、ユーザーが電話に与える使用法に従ってユーザーをセグメント化することです。これにより、マーケティング部門は各グループを異なる製品でターゲットにすることができます。
ナイーブベイズは、分類器を構築するための確率的手法です。単純ベイズ分類器の特徴的な仮定は、クラス変数が与えられた場合、特定の特徴の値が他の特徴の値から独立していると見なすことです。
前述の過度に単純化された仮定にもかかわらず、単純ベイズ分類器は、複雑な実世界の状況で良好な結果をもたらします。単純ベイズの利点は、分類に必要なパラメーターを推定するために必要なトレーニングデータが少量であり、分類器を段階的にトレーニングできることです。
ナイーブベイズは条件付き確率モデルです。分類される問題インスタンスが与えられ、ベクトルで表されます。 x=(x 1、…、x n)は、いくつかのn個の特徴(独立変数)を表し、K個の可能な結果またはクラスのそれぞれの確率をこのインスタンスに割り当てます。
$$p(C_k|x_1,....., x_n)$$
上記の定式化の問題は、特徴の数nが多い場合、または特徴が多数の値をとることができる場合、そのようなモデルを確率テーブルに基づくことは実行不可能であるということです。したがって、モデルを再定式化して、モデルを単純化します。ベイズの定理を使用すると、条件付き確率は次のように分解できます。
$$p(C_k|x) = \frac{p(C_k)p(x|C_k)}{p(x)}$$
これは、上記の独立性の仮定の下で、クラス変数Cの条件付き分布が-であることを意味します。
$$p(C_k|x_1,....., x_n)\: = \: \frac{1}{Z}p(C_k)\prod_{i = 1}^{n}p(x_i|C_k)$$
ここで、証拠Z = p(x)は、x 1、…、x nのみに依存するスケーリング係数であり、特徴変数の値がわかっている場合は定数です。一般的なルールの1つは、最も可能性の高い仮説を選択することです。これは、最大事後またはMAP決定ルールとして知られています。対応する分類器であるベイズ分類器は、クラスラベルを割り当てる関数です。$\hat{y} = C_k$ 次のようにいくつかのkについて-
$$\hat{y} = argmax\: p(C_k)\prod_{i = 1}^{n}p(x_i|C_k)$$
Rでアルゴリズムを実装するのは簡単なプロセスです。次の例は、単純ベイズ分類器をトレーニングし、スパムフィルタリング問題の予測に使用する方法を示しています。
次のスクリプトは、 bda/part3/naive_bayes/naive_bayes.R ファイル。
# Install these packages
pkgs = c("klaR", "caret", "ElemStatLearn")
install.packages(pkgs)
library('ElemStatLearn')
library("klaR")
library("caret")
# Split the data in training and testing
inx = sample(nrow(spam), round(nrow(spam) * 0.9))
train = spam[inx,]
test = spam[-inx,]
# Define a matrix with features, X_train
# And a vector with class labels, y_train
X_train = train[,-58]
y_train = train$spam X_test = test[,-58] y_test = test$spam
# Train the model
nb_model = train(X_train, y_train, method = 'nb',
trControl = trainControl(method = 'cv', number = 3))
# Compute
preds = predict(nb_model$finalModel, X_test)$class
tbl = table(y_test, yhat = preds)
sum(diag(tbl)) / sum(tbl)
# 0.7217391結果からわかるように、ナイーブベイズモデルの精度は72%です。これは、モデルがインスタンスの72%を正しく分類することを意味します。
k-meansクラスタリングは、n個の観測値をk個のクラスターに分割することを目的としています。このクラスターでは、各観測値が最も近い平均値を持つクラスターに属し、クラスターのプロトタイプとして機能します。これにより、データ空間がボロノイセルに分割されます。
一連の観測値(x 1、x 2、…、x n)が与えられ、各観測値はd次元の実数ベクトルである場合、k-meansクラスタリングは、n個の観測値をk個のグループに分割することを目的としていますG = {G 1、G 2、…、G k }は、次のように定義されるクラスター内の二乗和(WCSS)を最小化するようにします。
$$argmin \: \sum_{i = 1}^{k} \sum_{x \in S_{i}}\parallel x - \mu_{i}\parallel ^2$$
後者の式は、k-meansクラスタリングで最適なプロトタイプを見つけるために最小化される目的関数を示しています。式の直感は、互いに異なるグループを見つけたいということです。各グループの各メンバーは、各クラスターの他のメンバーと類似している必要があります。
次の例は、Rでk-meansクラスタリングアルゴリズムを実行する方法を示しています。
library(ggplot2)
# Prepare Data
data = mtcars
# We need to scale the data to have zero mean and unit variance
data <- scale(data)
# Determine number of clusters
wss <- (nrow(data)-1)*sum(apply(data,2,var))
for (i in 2:dim(data)[2]) {
wss[i] <- sum(kmeans(data, centers = i)$withinss)
}
# Plot the clusters
plot(1:dim(data)[2], wss, type = "b", xlab = "Number of Clusters",
ylab = "Within groups sum of squares")Kの適切な値を見つけるために、Kのさまざまな値のグループ内の二乗和をプロットできます。このメトリックは通常、グループが追加されるにつれて減少します。グループ内の合計の減少が減少するポイントを見つけたいと思います。正方形の数はゆっくりと減少し始めます。プロットでは、この値はK = 6で最もよく表されます。

Kの値が定義されたので、その値でアルゴリズムを実行する必要があります。
# K-Means Cluster Analysis
fit <- kmeans(data, 5) # 5 cluster solution
# get cluster means
aggregate(data,by = list(fit$cluster),FUN = mean)
# append cluster assignment
data <- data.frame(data, fit$cluster)してみましょう私は、I = 1、私は、2、...、私はn個のアイテムと呼ばれる一連のn個のバイナリ属性があること。ましょうD = T 1、T 2、...、T Mデータベースと呼ばれるトランザクションの集合です。Dの各トランザクションには一意のトランザクションIDがあり、Iのアイテムのサブセットが含まれています。ルールは、X⇒Yの形式の含意として定義されます。ここで、X、Y⊆IおよびX∩Y=∅です。
アイテムのセット(短いアイテムセットの場合)XおよびYは、ルールの前件(左側またはLHS)および後件(右側またはRHS)と呼ばれます。
概念を説明するために、スーパーマーケットドメインの小さな例を使用します。アイテムのセットはI = {牛乳、パン、バター、ビール}であり、アイテムを含む小さなデータベースを次の表に示します。
| トランザクションID | アイテム |
|---|---|
| 1 | 牛乳、パン |
| 2 | パン、バター |
| 3 | ビール |
| 4 | 牛乳、パン、バター |
| 5 | パン、バター |
スーパーマーケットのルールの例としては、{牛乳、パン}⇒{バター}があります。これは、牛乳とパンを購入すると、顧客もバターを購入することを意味します。考えられるすべてのルールのセットから興味深いルールを選択するために、重要性と関心のさまざまな尺度に対する制約を使用できます。最もよく知られている制約は、サポートと信頼性の最小しきい値です。
アイテムセットXのサポートsupp(X)は、アイテムセットを含むデータセット内のトランザクションの割合として定義されます。表1のデータベースの例では、アイテムセット{milk、bread}は、すべてのトランザクションの40%(5トランザクションのうち2トランザクション)で発生するため、2/5 = 0.4のサポートがあります。頻繁なアイテムセットを見つけることは、教師なし学習の問題を単純化したものと見なすことができます。
ルールの信頼度は、conf(X⇒Y)= supp(X∪Y)/ supp(X)で定義されます。たとえば、ルール{milk、bread}⇒{butter}は、表1のデータベースで0.2 / 0.4 = 0.5の信頼度を持っています。これは、牛乳とパンを含むトランザクションの50%でルールが正しいことを意味します。信頼度は、確率P(Y | X)の推定値として解釈できます。これは、トランザクションにLHSも含まれているという条件の下で、トランザクション内のルールのRHSを見つける確率です。
にあるスクリプトで bda/part3/apriori.R を実装するためのコード apriori algorithm 見つけることができます。
# Load the library for doing association rules
# install.packages(’arules’)
library(arules)
# Data preprocessing
data("AdultUCI")
AdultUCI[1:2,]
AdultUCI[["fnlwgt"]] <- NULL
AdultUCI[["education-num"]] <- NULL
AdultUCI[[ "age"]] <- ordered(cut(AdultUCI[[ "age"]], c(15,25,45,65,100)),
labels = c("Young", "Middle-aged", "Senior", "Old"))
AdultUCI[[ "hours-per-week"]] <- ordered(cut(AdultUCI[[ "hours-per-week"]],
c(0,25,40,60,168)), labels = c("Part-time", "Full-time", "Over-time", "Workaholic"))
AdultUCI[[ "capital-gain"]] <- ordered(cut(AdultUCI[[ "capital-gain"]],
c(-Inf,0,median(AdultUCI[[ "capital-gain"]][AdultUCI[[ "capitalgain"]]>0]),Inf)),
labels = c("None", "Low", "High"))
AdultUCI[[ "capital-loss"]] <- ordered(cut(AdultUCI[[ "capital-loss"]],
c(-Inf,0, median(AdultUCI[[ "capital-loss"]][AdultUCI[[ "capitalloss"]]>0]),Inf)),
labels = c("none", "low", "high"))aprioriアルゴリズムを使用してルールを生成するには、トランザクションマトリックスを作成する必要があります。次のコードは、Rでこれを行う方法を示しています。
# Convert the data into a transactions format
Adult <- as(AdultUCI, "transactions")
Adult
# transactions in sparse format with
# 48842 transactions (rows) and
# 115 items (columns)
summary(Adult)
# Plot frequent item-sets
itemFrequencyPlot(Adult, support = 0.1, cex.names = 0.8)
# generate rules
min_support = 0.01
confidence = 0.6
rules <- apriori(Adult, parameter = list(support = min_support, confidence = confidence))
rules
inspect(rules[100:110, ])
# lhs rhs support confidence lift
# {occupation = Farming-fishing} => {sex = Male} 0.02856148 0.9362416 1.4005486
# {occupation = Farming-fishing} => {race = White} 0.02831579 0.9281879 1.0855456
# {occupation = Farming-fishing} => {native-country 0.02671881 0.8758389 0.9759474
= United-States}決定木は、分類や回帰などの教師あり学習の問題に使用されるアルゴリズムです。決定木または分類木は、各内部(非葉)ノードが入力特徴でラベル付けされているツリーです。フィーチャでラベル付けされたノードからの円弧には、フィーチャの可能な値のそれぞれでラベルが付けられます。ツリーの各リーフには、クラスまたはクラス全体の確率分布のラベルが付けられています。
属性値テストに基づいてソースセットをサブセットに分割することにより、ツリーを「学習」できます。このプロセスは、派生したサブセットごとに、と呼ばれる再帰的な方法で繰り返されます。recursive partitioning。再帰は、ノードのサブセットのターゲット変数の値がすべて同じになったとき、または分割によって予測に値が追加されなくなったときに完了します。決定木のトップダウン誘導のこのプロセスは、欲張りアルゴリズムの例であり、決定木を学習するための最も一般的な戦略です。
データマイニングで使用される決定木には、主に2つのタイプがあります。
Classification tree −応答が名目変数である場合、たとえば、電子メールがスパムであるかどうか。
Regression tree −予測された結果が実数と見なされる場合(例:労働者の給与)。
決定木は単純な方法であるため、いくつかの問題があります。この問題の1つは、決定木が生成する結果のモデルの分散が大きいことです。この問題を軽減するために、決定木のアンサンブル手法が開発されました。現在広く使用されているアンサンブル手法には2つのグループがあります-
Bagging decision trees−これらのツリーは、トレーニングデータを繰り返しリサンプリングして置換し、コンセンサス予測に投票することで、複数の決定木を構築するために使用されます。このアルゴリズムはランダムフォレストと呼ばれています。
Boosting decision trees−勾配ブースティングは弱い学習者を組み合わせます。この場合、決定木は反復的に単一の強力な学習者になります。弱いツリーをデータに適合させ、前のモデルのエラーを修正するために弱い学習者を繰り返し適合させ続けます。
# Install the party package
# install.packages('party')
library(party)
library(ggplot2)
head(diamonds)
# We will predict the cut of diamonds using the features available in the
diamonds dataset.
ct = ctree(cut ~ ., data = diamonds)
# plot(ct, main="Conditional Inference Tree")
# Example output
# Response: cut
# Inputs: carat, color, clarity, depth, table, price, x, y, z
# Number of observations: 53940
#
# 1) table <= 57; criterion = 1, statistic = 10131.878
# 2) depth <= 63; criterion = 1, statistic = 8377.279
# 3) table <= 56.4; criterion = 1, statistic = 226.423
# 4) z <= 2.64; criterion = 1, statistic = 70.393
# 5) clarity <= VS1; criterion = 0.989, statistic = 10.48
# 6) color <= E; criterion = 0.997, statistic = 12.829
# 7)* weights = 82
# 6) color > E
#Table of prediction errors
table(predict(ct), diamonds$cut)
# Fair Good Very Good Premium Ideal
# Fair 1388 171 17 0 14
# Good 102 2912 499 26 27
# Very Good 54 998 3334 249 355
# Premium 44 711 5054 11915 1167
# Ideal 22 114 3178 1601 19988
# Estimated class probabilities
probs = predict(ct, newdata = diamonds, type = "prob")
probs = do.call(rbind, probs)
head(probs)ロジスティック回帰は、応答変数がカテゴリカルである分類モデルです。これは統計から得られるアルゴリズムであり、教師あり分類問題に使用されます。ロジスティック回帰では、コスト関数を最小化する次の方程式のパラメーターのベクトルβを見つけようとします。
$$logit(p_i) = ln \left ( \frac{p_i}{1 - p_i} \right ) = \beta_0 + \beta_1x_{1,i} + ... + \beta_kx_{k,i}$$
次のコードは、ロジスティック回帰モデルをRに適合させる方法を示しています。ここでは、スパムデータセットを使用して、ナイーブベイズで使用されたものと同じロジスティック回帰を示します。
精度に関する予測結果から、回帰モデルは、単純ベイズ分類器によって達成された72%と比較して、テストセットで92.5%の精度を達成することがわかります。
library(ElemStatLearn)
head(spam)
# Split dataset in training and testing
inx = sample(nrow(spam), round(nrow(spam) * 0.8))
train = spam[inx,]
test = spam[-inx,]
# Fit regression model
fit = glm(spam ~ ., data = train, family = binomial())
summary(fit)
# Call:
# glm(formula = spam ~ ., family = binomial(), data = train)
#
# Deviance Residuals:
# Min 1Q Median 3Q Max
# -4.5172 -0.2039 0.0000 0.1111 5.4944
# Coefficients:
# Estimate Std. Error z value Pr(>|z|)
# (Intercept) -1.511e+00 1.546e-01 -9.772 < 2e-16 ***
# A.1 -4.546e-01 2.560e-01 -1.776 0.075720 .
# A.2 -1.630e-01 7.731e-02 -2.108 0.035043 *
# A.3 1.487e-01 1.261e-01 1.179 0.238591
# A.4 2.055e+00 1.467e+00 1.401 0.161153
# A.5 6.165e-01 1.191e-01 5.177 2.25e-07 ***
# A.6 7.156e-01 2.768e-01 2.585 0.009747 **
# A.7 2.606e+00 3.917e-01 6.652 2.88e-11 ***
# A.8 6.750e-01 2.284e-01 2.955 0.003127 **
# A.9 1.197e+00 3.362e-01 3.559 0.000373 ***
# Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 . 0.1 1
### Make predictions
preds = predict(fit, test, type = ’response’)
preds = ifelse(preds > 0.5, 1, 0)
tbl = table(target = test$spam, preds)
tbl
# preds
# target 0 1
# email 535 23
# spam 46 316
sum(diag(tbl)) / sum(tbl)
# 0.925時系列は、日付またはタイムスタンプでインデックス付けされたカテゴリ変数または数値変数の一連の観測値です。時系列データの明確な例は、株価の時系列です。次の表に、時系列データの基本構造を示します。この場合、観測は1時間ごとに記録されます。
| タイムスタンプ | 株価 |
|---|---|
| 2015-10-11 09:00:00 | 100 |
| 2015-10-11 10:00:00 | 110 |
| 2015-10-11 11:00:00 | 105 |
| 2015-10-11 12:00:00 | 90 |
| 2015-10-11 13:00:00 | 120 |
通常、時系列分析の最初のステップは系列をプロットすることです。これは通常、折れ線グラフを使用して行われます。
時系列分析の最も一般的なアプリケーションは、データの時間的構造を使用して数値の将来の値を予測することです。これは、利用可能な観測値を使用して、将来の値を予測することを意味します。
データの時間的順序は、従来の回帰法が役に立たないことを意味します。堅牢な予測を構築するには、データの時間的順序を考慮したモデルが必要です。
時系列分析で最も広く使用されているモデルは、 Autoregressive Moving Average(ARMA)。モデルは2つの部分で構成されています。autoregressive (AR)部分と moving average(MA)パート。このモデルは通常、ARMA(p、q)モデルと呼ばれます。ここで、pは自己回帰部分の次数であり、qは移動平均部分の次数です。
自己回帰モデル
AR(p)はp次の自己回帰モデルとして読み出されます。数学的には次のように記述されます-
$$ X_t = c + \ sum_ {i = 1} ^ {P} \ phi_i X_ {t --i} + \ varepsilon_ {t} $$
ここで、{φ 1、...、φ pは}推定されるパラメータであり、Cは定数であり、ランダム変数ε tは白色ノイズを表しています。モデルが静止したままになるように、パラメーターの値にいくつかの制約が必要です。
移動平均
表記MA(q)は、次数q −の移動平均モデルを指します。
$$ X_t = \ mu + \ varepsilon_t + \ sum_ {i = 1} ^ {q} \ theta_i \ varepsilon_ {t --i} $$
θ場合を1、...、θ qはモデルのパラメータであり、μは、Xの期待値であり、T、及びε T、ε T - 1、...、白色雑音誤差項です。
自己回帰移動平均
ARMA(P、Q)モデルコンバインPの自己回帰用語およびq移動平均用語。数学的には、モデルは次の式で表されます。
$$ X_t = c + \ varepsilon_t + \ sum_ {i = 1} ^ {P} \ phi_iX_ {t-1} + \ sum_ {i = 1} ^ {q} \ theta_i \ varepsilon_ {ti} $$
ARMA(p、q)モデルはAR(p )モデルとMA(q)モデルの組み合わせであることがわかります。
モデルのいくつかの直感を与えるために式のAR部分がXのためのパラメータを推定しようと考えている私- T Xの中の変数の値を予測するためにの観測をトンを。最終的には、過去の値の加重平均になります。MAセクションは同じアプローチを使用しますが、以前の観測の誤差、εt −iがあります。したがって、最終的に、モデルの結果は加重平均になります。
次のコードスニペットは、RでARMA(p、q)を実装する方法を示しています。
# install.packages("forecast")
library("forecast")
# Read the data
data = scan('fancy.dat')
ts_data <- ts(data, frequency = 12, start = c(1987,1))
ts_data
plot.ts(ts_data)データのプロットは通常、データに時間的構造があるかどうかを確認するための最初のステップです。プロットから、毎年の終わりに強いスパイクがあることがわかります。
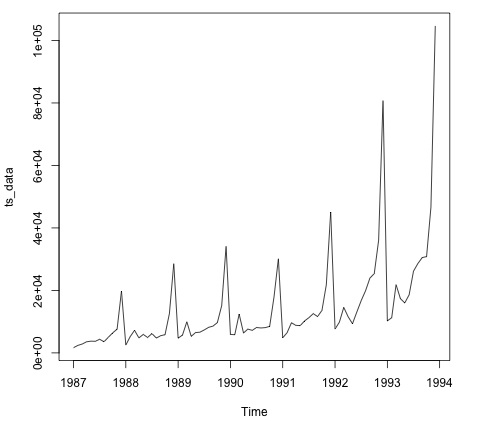
次のコードは、ARMAモデルをデータに適合させます。モデルのいくつかの組み合わせを実行し、エラーの少ないモデルを選択します。
# Fit the ARMA model
fit = auto.arima(ts_data)
summary(fit)
# Series: ts_data
# ARIMA(1,1,1)(0,1,1)[12]
# Coefficients:
# ar1 ma1 sma1
# 0.2401 -0.9013 0.7499
# s.e. 0.1427 0.0709 0.1790
#
# sigma^2 estimated as 15464184: log likelihood = -693.69
# AIC = 1395.38 AICc = 1395.98 BIC = 1404.43
# Training set error measures:
# ME RMSE MAE MPE MAPE MASE ACF1
# Training set 328.301 3615.374 2171.002 -2.481166 15.97302 0.4905797 -0.02521172この章では、本のパート1でスクレイピングされたデータを使用します。データには、フリーランサーのプロファイルと、彼らが米ドルで請求している時給を説明するテキストが含まれています。次のセクションのアイデアは、フリーランサーのスキルを考慮して、その時給を予測できるモデルに適合させることです。
次のコードは、この場合、単語の袋のマトリックスでユーザーのスキルを持つ生のテキストを変換する方法を示しています。このために、tmと呼ばれるRライブラリを使用します。これは、コーパス内の単語ごとに、各変数の出現回数で変数を作成することを意味します。
library(tm)
library(data.table)
source('text_analytics/text_analytics_functions.R')
data = fread('text_analytics/data/profiles.txt')
rate = as.numeric(data$rate)
keep = !is.na(rate)
rate = rate[keep]
### Make bag of words of title and body
X_all = bag_words(data$user_skills[keep])
X_all = removeSparseTerms(X_all, 0.999)
X_all
# <<DocumentTermMatrix (documents: 389, terms: 1422)>>
# Non-/sparse entries: 4057/549101
# Sparsity : 99%
# Maximal term length: 80
# Weighting : term frequency - inverse document frequency (normalized) (tf-idf)
### Make a sparse matrix with all the data
X_all <- as_sparseMatrix(X_all)これで、テキストがスパース行列として表されたので、スパース解を与えるモデルを適合させることができます。この場合の適切な代替手段は、LASSO(最小絶対収縮および選択演算子)を使用することです。これは、ターゲットを予測するために最も関連性の高い機能を選択できる回帰モデルです。
train_inx = 1:200
X_train = X_all[train_inx, ]
y_train = rate[train_inx]
X_test = X_all[-train_inx, ]
y_test = rate[-train_inx]
# Train a regression model
library(glmnet)
fit <- cv.glmnet(x = X_train, y = y_train,
family = 'gaussian', alpha = 1,
nfolds = 3, type.measure = 'mae')
plot(fit)
# Make predictions
predictions = predict(fit, newx = X_test)
predictions = as.vector(predictions[,1])
head(predictions)
# 36.23598 36.43046 51.69786 26.06811 35.13185 37.66367
# We can compute the mean absolute error for the test data
mean(abs(y_test - predictions))
# 15.02175これで、一連のスキルが与えられた場合に、フリーランサーの時給を予測できるモデルができました。より多くのデータが収集されると、モデルのパフォーマンスは向上しますが、このパイプラインを実装するためのコードは同じになります。
オンライン学習は、教師あり学習モデルを大規模なデータセットにスケーリングできる機械学習のサブフィールドです。基本的な考え方は、モデルに合わせるためにメモリ内のすべてのデータを読み取る必要はなく、一度に各インスタンスを読み取るだけでよいということです。
この場合、ロジスティック回帰を使用してオンライン学習アルゴリズムを実装する方法を示します。ほとんどの教師あり学習アルゴリズムと同様に、最小化されたコスト関数があります。ロジスティック回帰では、コスト関数は次のように定義されます。
$$ J(\ theta)\:= \:\ frac {-1} {m} \ left [\ sum_ {i = 1} ^ {m} y ^ {(i)} log(h _ {\ theta}( x ^ {(i)}))+(1-y ^ {(i)})log(1-h _ {\ theta}(x ^ {(i)}))\ right] $$
ここで、J(θ)は、コスト関数を表し、H θ(x)は仮説を表します。ロジスティック回帰の場合、次の式で定義されます。
$$ h_ \ theta(x)= \ frac {1} {1 + e ^ {\ theta ^ T x}} $$
コスト関数を定義したので、それを最小化するアルゴリズムを見つける必要があります。これを達成するための最も単純なアルゴリズムは、確率的勾配降下法と呼ばれます。ロジスティック回帰モデルの重みのアルゴリズムの更新ルールは、次のように定義されます。
$$ \ theta_j:= \ theta_j- \ alpha(h_ \ theta(x)-y)x $$
次のアルゴリズムにはいくつかの実装がありますが、vowpalwabbitライブラリに実装されているものが最も開発されたものです。このライブラリは、大規模な回帰モデルのトレーニングを可能にし、少量のRAMを使用します。作成者自身の言葉では、「Vowpal Wabbit(VW)プロジェクトは、Microsoft Researchおよび(以前の)Yahoo!Researchが後援する高速のアウトオブコア学習システムです」と説明されています。
からのタイタニックデータセットを使用します kaggleコンペ。元のデータはにありますbda/part3/vwフォルダ。ここに、2つのファイルがあります-
- トレーニングデータ(train_titanic.csv)があり、
- 新しい予測を行うためのラベルなしデータ(test_titanic.csv)。
csv形式をに変換するには vowpal wabbit 入力形式は csv_to_vowpal_wabbit.pyPythonスクリプト。これには明らかにPythonをインストールする必要があります。に移動しますbda/part3/vw フォルダ、ターミナルを開き、次のコマンドを実行します-
python csv_to_vowpal_wabbit.pyこのセクションでは、Windowsを使用している場合は、Unixコマンドラインをインストールする必要があることに注意してください。そのためにcygwinWebサイトにアクセスしてください。
ターミナルとフォルダを開きます bda/part3/vw 次のコマンドを実行します-
vw train_titanic.vw -f model.vw --binary --passes 20 -c -q ff --sgd --l1
0.00000001 --l2 0.0000001 --learning_rate 0.5 --loss_function logisticの各引数が何であるかを分解しましょう vw call 手段。
-f model.vw −後で予測を行うためにモデルをmodel.vwファイルに保存していることを意味します
--binary −-1,1ラベルのバイナリ分類として損失を報告します
--passes 20 −データは重みを学習するために20回使用されます
-c −キャッシュファイルを作成する
-q ff −f名前空間で2次関数を使用する
--sgd −通常/古典的/単純な確率的勾配降下法の更新を使用します。つまり、非適応、非正規化、および非不変です。
--l1 --l2 −L1およびL2ノルムの正則化
--learning_rate 0.5 −更新ルール式で定義された学習率α
次のコードは、コマンドラインで回帰モデルを実行した結果を示しています。結果では、平均ログ損失とアルゴリズムパフォーマンスの小さなレポートが得られます。
-loss_function logistic
creating quadratic features for pairs: ff
using l1 regularization = 1e-08
using l2 regularization = 1e-07
final_regressor = model.vw
Num weight bits = 18
learning rate = 0.5
initial_t = 1
power_t = 0.5
decay_learning_rate = 1
using cache_file = train_titanic.vw.cache
ignoring text input in favor of cache input
num sources = 1
average since example example current current current
loss last counter weight label predict features
0.000000 0.000000 1 1.0 -1.0000 -1.0000 57
0.500000 1.000000 2 2.0 1.0000 -1.0000 57
0.250000 0.000000 4 4.0 1.0000 1.0000 57
0.375000 0.500000 8 8.0 -1.0000 -1.0000 73
0.625000 0.875000 16 16.0 -1.0000 1.0000 73
0.468750 0.312500 32 32.0 -1.0000 -1.0000 57
0.468750 0.468750 64 64.0 -1.0000 1.0000 43
0.375000 0.281250 128 128.0 1.0000 -1.0000 43
0.351562 0.328125 256 256.0 1.0000 -1.0000 43
0.359375 0.367188 512 512.0 -1.0000 1.0000 57
0.274336 0.274336 1024 1024.0 -1.0000 -1.0000 57 h
0.281938 0.289474 2048 2048.0 -1.0000 -1.0000 43 h
0.246696 0.211454 4096 4096.0 -1.0000 -1.0000 43 h
0.218922 0.191209 8192 8192.0 1.0000 1.0000 43 h
finished run
number of examples per pass = 802
passes used = 11
weighted example sum = 8822
weighted label sum = -2288
average loss = 0.179775 h
best constant = -0.530826
best constant’s loss = 0.659128
total feature number = 427878これで、 model.vw 新しいデータで予測を生成するようにトレーニングしました。
vw -d test_titanic.vw -t -i model.vw -p predictions.txt前のコマンドで生成された予測は、[0、1]の範囲に収まるように正規化されていません。これを行うために、シグモイド変換を使用します。
# Read the predictions
preds = fread('vw/predictions.txt')
# Define the sigmoid function
sigmoid = function(x) {
1 / (1 + exp(-x))
}
probs = sigmoid(preds[[1]])
# Generate class labels
preds = ifelse(probs > 0.5, 1, 0)
head(preds)
# [1] 0 1 0 0 1 0