ビッグデータ分析-チャートとグラフ
データを分析するための最初のアプローチは、データを視覚的に分析することです。これを行う目的は、通常、変数と変数の単変量記述の間の関係を見つけることです。これらの戦略は次のように分けることができます-
- 単変量分析
- 多変量解析
単変量グラフィカルメソッド
Univariateは統計用語です。実際には、残りのデータから独立して変数を分析したいということです。これを効率的に行うことができるプロットは次のとおりです。
箱ひげ図
箱ひげ図は通常、分布を比較するために使用されます。これは、分布間に違いがあるかどうかを視覚的に検査するための優れた方法です。カットごとにダイヤモンドの価格に違いがあるかどうかを確認できます。
# We will be using the ggplot2 library for plotting
library(ggplot2)
data("diamonds")
# We will be using the diamonds dataset to analyze distributions of numeric variables
head(diamonds)
# carat cut color clarity depth table price x y z
# 1 0.23 Ideal E SI2 61.5 55 326 3.95 3.98 2.43
# 2 0.21 Premium E SI1 59.8 61 326 3.89 3.84 2.31
# 3 0.23 Good E VS1 56.9 65 327 4.05 4.07 2.31
# 4 0.29 Premium I VS2 62.4 58 334 4.20 4.23 2.63
# 5 0.31 Good J SI2 63.3 58 335 4.34 4.35 2.75
# 6 0.24 Very Good J VVS2 62.8 57 336 3.94 3.96 2.48
### Box-Plots
p = ggplot(diamonds, aes(x = cut, y = price, fill = cut)) +
geom_box-plot() +
theme_bw()
print(p)プロットでは、カットの種類によってダイヤモンドの価格の分布に違いがあることがわかります。

ヒストグラム
source('01_box_plots.R')
# We can plot histograms for each level of the cut factor variable using
facet_grid
p = ggplot(diamonds, aes(x = price, fill = cut)) +
geom_histogram() +
facet_grid(cut ~ .) +
theme_bw()
p
# the previous plot doesn’t allow to visuallize correctly the data because of
the differences in scale
# we can turn this off using the scales argument of facet_grid
p = ggplot(diamonds, aes(x = price, fill = cut)) +
geom_histogram() +
facet_grid(cut ~ ., scales = 'free') +
theme_bw()
p
png('02_histogram_diamonds_cut.png')
print(p)
dev.off()上記のコードの出力は次のようになります-
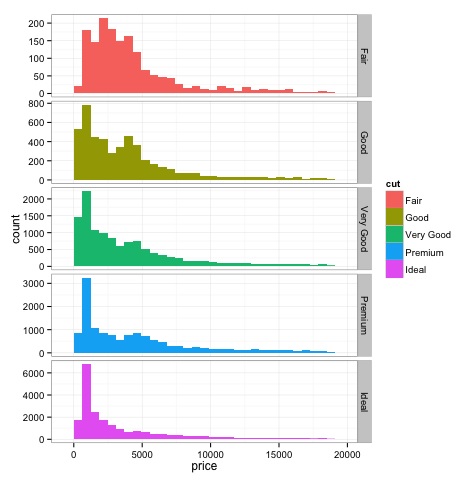
多変量グラフィカルメソッド
探索的データ分析における多変量グラフィカル手法には、さまざまな変数間の関係を見つけることを目的としています。これを実現するには、一般的に使用される2つの方法があります。数値変数の相関行列をプロットする方法と、単に散布図の行列として生データをプロットする方法です。
これを示すために、diamondsデータセットを使用します。コードに従うには、スクリプトを開きますbda/part2/charts/03_multivariate_analysis.R。
library(ggplot2)
data(diamonds)
# Correlation matrix plots
keep_vars = c('carat', 'depth', 'price', 'table')
df = diamonds[, keep_vars]
# compute the correlation matrix
M_cor = cor(df)
# carat depth price table
# carat 1.00000000 0.02822431 0.9215913 0.1816175
# depth 0.02822431 1.00000000 -0.0106474 -0.2957785
# price 0.92159130 -0.01064740 1.0000000 0.1271339
# table 0.18161755 -0.29577852 0.1271339 1.0000000
# plots
heat-map(M_cor)コードは次の出力を生成します-

これは要約であり、価格とキャレットの間には強い相関関係があり、他の変数の間にはそれほど多くないことがわかります。
相関行列は、変数が多数ある場合に役立ちます。その場合、生データのプロットは実用的ではありません。前述のように、生データを表示することも可能です-
library(GGally)
ggpairs(df)ヒートマップに表示された結果が確認されていることがプロットでわかります。価格とカラットの変数の間には0.922の相関関係があります。
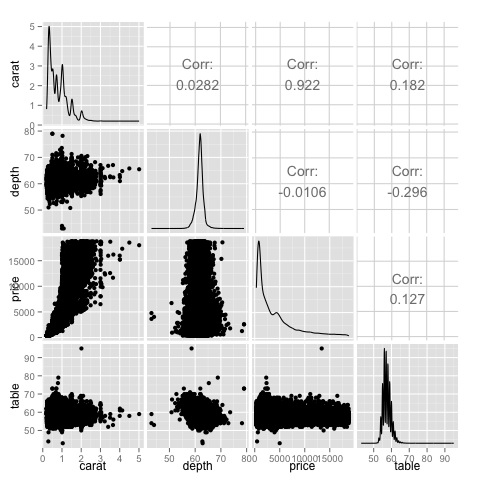
この関係は、散布図行列の(3、1)インデックスにある価格カラット散布図で視覚化できます。