集積回路の基礎
アン electronic circuit 特定の目的のために接続された電子部品のグループです。
簡単な電子回路は、個別の電子部品や接続がほとんど必要ないため、簡単に設計できます。ただし、複雑な電子回路を設計することは、より多くの個別の電子部品とそれらの接続を必要とするため、困難です。また、このような複雑な回路を構築するには時間がかかり、信頼性も低くなります。これらの困難は集積回路で克服することができます。
集積回路(IC)
複数の電子部品が半導体材料の単一チップ上で相互接続されている場合、そのチップは Integrated Circuit (IC)。これは、アクティブコンポーネントとパッシブコンポーネントの両方で構成されています。
この章では、ICの利点と種類について説明します。
集積回路の利点
集積回路には多くの利点があります。それらについては以下で説明します-
Compact size −特定の機能について、ディスクリート回路を使用して構築された回路と比較して、ICを使用してより小さなサイズの回路を取得できます。
Lesser weight− ICで構築された回路は、ICの同じ機能を実装するために使用されるディスクリート回路の重量と比較して軽量です。ディスクリート回路を使用して構築されたものと比較して、ICを使用します。
Low power consumption − ICは、サイズと構造が小さいため、従来の回路よりも消費電力が少なくなります。
Reduced cost − ICは、製造技術とディスクリート回路よりも少ない材料の使用により、ディスクリート回路よりもはるかに低コストで入手できます。
Increased reliability −接続数が少ないため、ICはデジタル回路に比べて信頼性が向上します。
Improved operating speeds − ICは、スイッチング速度と消費電力が少ないため、速度が向上しています。
集積回路の種類
集積回路には2つのタイプがあります − Analog Integrated Circuits and Digital Integrated Circuits。
アナログ集積回路
信号振幅の連続値の全範囲で動作する集積回路は、次のように呼ばれます。 Analog Integrated Circuits. これらは、ここで説明するように、さらに2つのタイプに分類されます-
Linear Integrated Circuits−アナログICは、その電圧と電流の間に線形関係が存在する場合、線形であると言われます。8ピンデュアルインラインパッケージ(DIP)オペアンプであるIC 741は、リニアICの一例です。
Radio Frequency Integrated Circuits−アナログICは、その電圧と電流の間に非線形の関係が存在する場合、非線形であると言われます。非線形ICは無線周波数ICとも呼ばれます。
デジタル集積回路
集積回路が信号振幅の連続値の全範囲で動作するのではなく、いくつかの事前定義されたレベルでのみ動作する場合、それらは次のように呼ばれます。 Digital Integrated Circuits。
次の章では、さまざまな線形集積回路とそのアプリケーションについて説明します。
オペアンプは、オペアンプとも呼ばれ、さまざまな線形、非線形、および数学演算を実行するために使用できる集積回路です。オペアンプはdirect coupled high gain amplifier。AC信号とDC信号の両方でオペアンプを操作できます。この章では、オペアンプの特性とタイプについて説明します。
オペアンプの構築
オペアンプは、差動アンプ、レベルトランスレータ、および出力段で構成されています。差動アンプはオペアンプの入力段に存在するため、オペアンプはtwo input terminals。それらの端末の1つはinverting terminal もう1つは non-inverting terminal。端子は、それぞれの入力と出力の間の位相関係に基づいて名前が付けられています。
オペアンプの特性
オペアンプの重要な特性またはパラメータは次のとおりです。
- 開ループ電圧利得
- 出力オフセット電圧
- 同相信号除去比
- スルーレート
このセクションでは、以下に示すように、これらの特性について詳しく説明します。
開ループ電圧利得
オペアンプの開ループ電圧ゲインは、フィードバックパスのない差動ゲインです。
数学的には、オペアンプの開ループ電圧ゲインは次のように表されます。
$$A_{v}= \frac{v_0}{v_1-v_2}$$
出力オフセット電圧
差動入力電圧がゼロのときにオペアンプの出力に存在する電圧は、次のように呼ばれます。 output offset voltage.
同相信号除去比
同相信号除去比(CMRR)オペアンプの)は、閉ループ差動ゲインの比率として定義されます。 $A_{d}$ コモンモードゲイン、 $A_{c}$。
数学的には、CMRRは次のように表すことができます。
$$CMRR=\frac{A_{d}}{A_{c}}$$
コモンモードゲインに注意してください。 $A_{c}$ オペアンプのは、コモンモード出力電圧とコモンモード入力電圧の比率です。
スルーレート
オペアンプのスルーレートは、ステップ入力電圧による出力電圧の最大変化率として定義されます。
数学的には、スルーレート(SR)は次のように表すことができます。
$$SR=Maximum\:of\:\frac{\text{d}V_{0}}{\text{d}t}$$
どこ、 $V_{0}$は出力電圧です。一般的に、スルーレートはどちらかで測定されます$V/\mu\:Sec$ または $V/m\:Sec$。
オペアンプの種類
オペアンプは、2つの入力と1つの出力を持つ三角形の記号で表されます。
オペアンプには次の2つのタイプがあります。 Ideal Op-Amp そして Practical Op-Amp。
それらは以下のように詳細に議論されます-
理想的なオペアンプ
理想的なオペアンプは理論上のみ存在し、実際には存在しません。ザ・equivalent circuit 理想的なオペアンプの特性を下の図に示します-
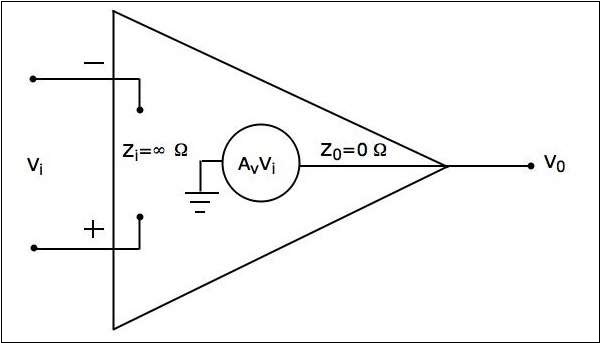
アン ideal op-amp 以下の特性を示します-
入力インピーダンス $Z_{i}=\infty\Omega$
出力インピーダンス $Z_{0}=0\Omega$
開ループ電圧ゲイン $A_{v}=\infty$
(差動)入力電圧の場合 $V_{i}=0V$の場合、出力電圧は次のようになります。 $V_{0}=0V$
帯域幅は infinity。つまり、理想的なオペアンプは、減衰することなく任意の周波数の信号を増幅します。
同相信号除去比 (CMRR) です infinity。
スルーレート (SR) です infinity。つまり、理想的なオペアンプは、入力ステップ電圧に応答して即座に出力に変化をもたらします。
実用的なオペアンプ
実際には、オペアンプは理想的ではなく、製造中のいくつかの欠陥のために理想的な特性から逸脱しています。ザ・equivalent circuit 実用的なオペアンプの概要を次の図に示します。
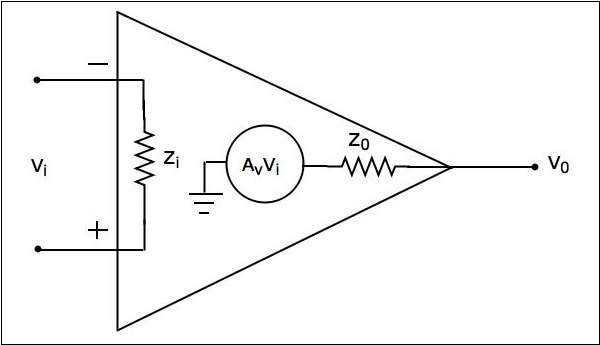
A practical op-amp 以下の特性を示します-
入力インピーダンス、 $Z_{i}$ の順に Mega ohms。
出力インピーダンス、 $Z_{0}$ の順に few ohms.。
開ループ電圧利得、 $A_{v}$ になります high。
実用的なオペアンプを選ぶときは、以下の条件を満たすかどうかを確認する必要があります。
入力インピーダンス、 $Z_{i}$ できるだけ高くする必要があります。
出力インピーダンス、 $Z_{0}$ できるだけ低くする必要があります。
開ループ電圧利得、 $A_{v}$ できるだけ高くする必要があります。
出力オフセット電圧は可能な限り低くする必要があります。
動作帯域幅は可能な限り高くする必要があります。
CMRRは可能な限り高くする必要があります。
スルーレートは可能な限り高くする必要があります。
Note − IC 741オペアンプは、最も人気があり実用的なオペアンプです。
回路は linear、入力と出力の間に線形関係が存在する場合。同様に、回路はnon-linear、入力と出力の間に非線形の関係が存在する場合。
オペアンプは、線形アプリケーションと非線形アプリケーションの両方で使用できます。以下は、オペアンプの基本的なアプリケーションです。
- 反転増幅器
- 非反転アンプ
- ボルテージフォロワー
この章では、これらの基本的なアプリケーションについて詳しく説明します。
反転増幅器
反転増幅器は、抵抗を介してその反転端子を介して入力を受け取ります $R_{1}$、およびその増幅されたバージョンを出力として生成します。このアンプは、入力を増幅するだけでなく、入力を反転(符号を変更)します。
ザ・ circuit diagram 反転増幅器の特性を次の図に示します。
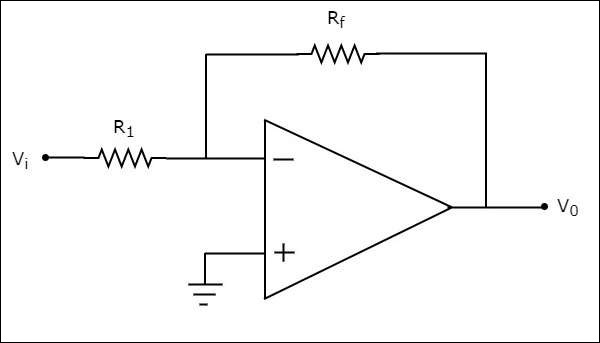
オペアンプの場合、反転入力端子の電圧は非反転入力端子の電圧と等しいことに注意してください。物理的には、これら2つの端末間に短絡はありませんがvirtually、彼らは short お互いに。
上記の回路では、非反転入力端子はグランドに接続されています。これは、オペアンプの非反転入力端子にゼロボルトが印加されることを意味します。
による virtual short concept、オペアンプの反転入力端子の電圧はゼロボルトになります。
ザ・ nodal equation この端末のノードは以下のようになります−
$$\frac{0-V_i}{R_1}+ \frac{0-V_0}{R_f}=0$$
$$=>\frac{-V_i}{R_1}= \frac{V_0}{R_f}$$
$$=>V_{0}=\left(\frac{-R_f}{R_1}\right)V_{t}$$
$$=>\frac{V_0}{V_i}= \frac{-R_f}{R_1}$$
出力電圧の比率 $V_{0}$ および入力電圧 $V_{i}$は、アンプの電圧ゲインまたはゲインです。したがって、gain of inverting amplifier に等しい $-\frac{R_f}{R_1}$。
反転増幅器のゲインは、 negative sign。それは180が存在することを示す0の入力と出力の間の位相差を。
非反転アンプ
非反転増幅器は、非反転端子を介して入力を受け取り、その増幅されたバージョンを出力として生成します。名前が示すように、このアンプは、出力の符号を反転または変更することなく、入力を増幅するだけです。
ザ・ circuit diagram 非反転増幅器の特性を次の図に示します。
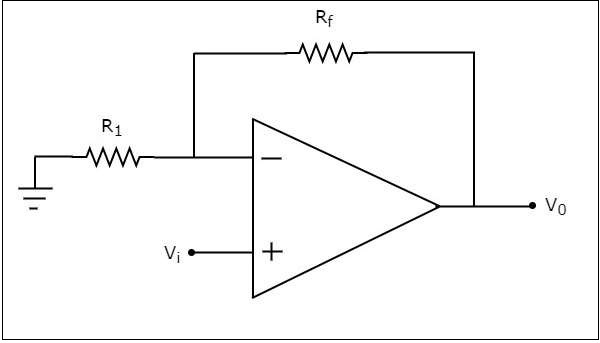
上記の回路では、入力電圧 $V_{i}$オペアンプの非反転入力端子に直接適用されます。したがって、オペアンプの非反転入力端子の電圧は次のようになります。$V_{i}$。
を使用して voltage division principle、以下に示すように、オペアンプの反転入力端子の電圧を計算できます。
$$=>V_{1} = V_{0}\left(\frac{R_1}{R_1+R_f}\right)$$
による virtual short concept、オペアンプの反転入力端子の電圧は、非反転入力端子の電圧と同じです。
$$=>V_{1} = V_{i}$$
$$=>V_{0}\left(\frac{R_1}{R_1+R_f}\right)=V_{i}$$
$$=>\frac{V_0}{V_i}=\frac{R_1+R_f}{R_1}$$
$$=>\frac{V_0}{V_i}=1+\frac{R_f}{R_1}$$
さて、出力電圧の比率 $V_{0}$ および入力電圧 $V_{i}$ または電圧ゲインまたは gain of the non-inverting amplifier に等しい $1+\frac{R_f}{R_1}$。
非反転増幅器のゲインは、 positive sign。入力と出力の間に位相差がないことを示します。
ボルテージフォロワー
A voltage followerは、入力電圧に追従する出力を生成する電子回路です。これは、非反転アンプの特殊なケースです。
フィードバック抵抗の値を考慮すると、 $R_{f}$ゼロオームおよび(または)抵抗の値として、1を無限大オームとして、非反転増幅器は電圧フォロワになります。ザ・circuit diagram ボルテージフォロワの特性を次の図に示します。

上記の回路では、入力電圧 $V_{i}$オペアンプの非反転入力端子に直接適用されます。したがって、オペアンプの非反転入力端子の電圧は次のようになります。$V_{i}$。ここで、出力はオペアンプの反転入力端子に直接接続されています。したがって、オペアンプの反転入力端子の電圧は次のようになります。$V_{0}$。
による virtual short concept、オペアンプの反転入力端子の電圧は、非反転入力端子の電圧と同じです。
$$=>V_{0} = V_{i}$$
だから、出力電圧 $V_{0}$ 電圧フォロワのはその入力電圧に等しい $V_{i}$。
したがって、 gain of a voltage follower 両方の出力電圧が1であるため、 $V_{0}$ および入力電圧 $V_{i}$ ボルテージフォロワのは同じです。
前の章では、オペアンプの基本的なアプリケーションについて説明しました。それらはオペアンプの線形演算の下にあることに注意してください。この章では、オペアンプの線形アプリケーションでもある算術回路について説明します。
算術演算を実行する電子回路は、 arithmetic circuits。オペアンプを使用すると、次のような基本的な算術回路を構築できます。adder と subtractor。この章では、それぞれについて詳しく学習します。
加算器
加算器は、適用された入力の合計に等しい出力を生成する電子回路です。このセクションでは、オペアンプベースの加算回路について説明します。
オペアンプベースの加算器は、その反転端子に印加された入力電圧の合計に等しい出力を生成します。とも呼ばれますsumming amplifier、出力は増幅されたものであるため。
ザ・ circuit diagram オペアンプベースの加算器の特性を次の図に示します-
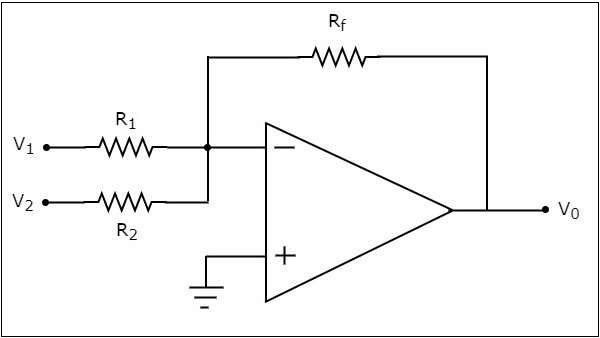
上記の回路では、オペアンプの非反転入力端子はグランドに接続されています。これは、非反転入力端子にゼロボルトが印加されることを意味します。
による virtual short concept、オペアンプの反転入力端子の電圧は、非反転入力端子の電圧と同じです。したがって、オペアンプの反転入力端子の電圧はゼロボルトになります。
ザ・ nodal equation 反転入力端子のノードは
$$\frac{0-V_1}{R_1}+\frac{0-V_2}{R_2}+\frac{0-V_0}{R_f}=0$$
$$=>\frac{V_1}{R_1}-\frac{V_2}{R_2}=\frac{V_0}{R_f}$$
$$=>V_{0}=R_{f}\left(\frac{V_1}{R_1}+\frac{V_2}{R_2}\right)$$
場合 $R_{f}=R_{1}=R_{2}=R$、次に出力電圧 $V_{0}$ −になります
$$V_{0}=-R{}\left(\frac{V_1}{R}+\frac{V_2}{R}\right)$$
$$=>V_{0}=-(V_{1}+V_{2})$$
したがって、上記のオペアンプベースの加算回路は、2つの入力電圧の合計を生成します。 $v_{1}$ そして $v_{1}$、出力として、回路に存在するすべての抵抗が同じ値の場合。出力電圧に注意してください$V_{0}$ 加算器回路の negative sign、180が存在することを示す0の入力と出力の間の位相差。
減算器
減算器は、適用された入力の差に等しい出力を生成する電子回路です。このセクションでは、オペアンプベースの減算回路について説明します。
オペアンプベースの減算器は、反転端子と非反転端子に印加された入力電圧の差に等しい出力を生成します。とも呼ばれますdifference amplifier、出力は増幅されたものであるため。
ザ・ circuit diagram オペアンプベースの減算器の特性を次の図に示します。
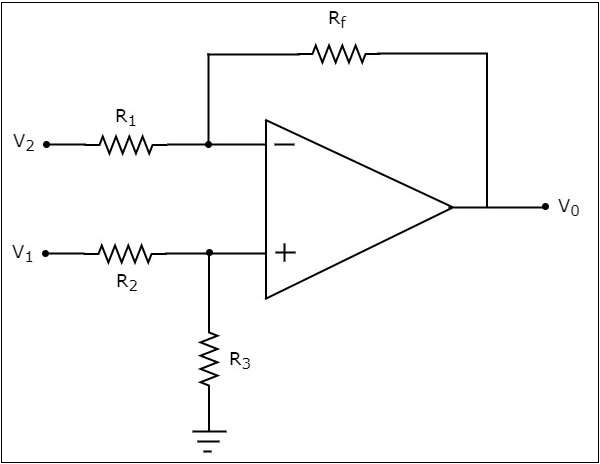
ここで、出力電圧の式を見つけましょう。 $V_{0}$ 上記の回路の superposition theorem 次の手順を使用して-
ステップ1
まず、出力電圧を計算してみましょう $V_{01}$ のみを考慮することによって $V_{1}$。
このために、 $V_{2}$それを短絡させることによって。次に、modified circuit diagram 次の図に示すように-

今、を使用して voltage division principle、オペアンプの非反転入力端子の電圧を計算します。
$$=>V_{p}=V_{1}\left(\frac{R_3}{R_2+R_3}\right)$$
さて、上記の回路は入力電圧を持つ非反転増幅器のように見えます $V_{p}$。したがって、出力電圧$V_{01}$ 上記の回路の
$$V_{01}=V_{p}\left(1+\frac{R_f}{R_1}\right)$$
代用、の値 $V_{p}$ 上記の式で、出力電圧を取得します。 $V_{01}$ のみを考慮することによって $V_{1}$、as −
$$V_{01}=V_{1}\left(\frac{R_3}{R_2+R_3}\right)\left(1+\frac{R_f}{R_1}\right)$$
ステップ2
このステップでは、出力電圧を見つけましょう。 $V_{02}$ のみを考慮することによって $V_{2}$。上記の手順と同様に、$V_{1}$それを短絡させることによって。ザ・modified circuit diagram 次の図に示します。

オペアンプの非反転入力端子の電圧がゼロボルトになることがわかります。つまり、上記の回路は単にinverting op-amp。したがって、出力電圧$V_{02}$ 上記の回路のは-になります
$$V_{02}=\left(-\frac{R_f}{R_1}\right)V_{2}$$
ステップ3
このステップでは、出力電圧を取得します $V_{0}$ による減算回路の adding the output voltagesステップ1とステップ2で取得します。数学的には、次のように書くことができます
$$V_{0}=V_{01}+V_{02}$$
の値を代入する $V_{01}$ そして $V_{02}$ 上記の式では、次のようになります。
$$V_{0}=V_{1}\left(\frac{R_3}{R_2+R_3}\right)\left(1+\frac{R_f}{R_1}\right)+\left(-\frac{R_f}{R_1}\right)V_{2}$$
$$=>V_{0}=V_{1}\left(\frac{R_3}{R_2+R_3}\right)\left(1+\frac{R_f}{R_1}\right)-\left(\frac{R_f}{R_1}\right)V_{2}$$
場合 $R_{f}=R_{1}=R_{2}=R_{3}=R$、次に出力電圧 $V_{0}$ になります
$$V_{0}=V_{1}\left(\frac{R}{R+R}\right)\left(1+\frac{R}{R}\right)-\left(\frac{R}{R}\right)V_{2}$$
$$=>V_{0}=V_{1}\left(\frac{R}{2R}\right)(2)-(1)V_{2}$$
$$V_{0}=V_{1}-V_{2}$$
したがって、上記のオペアンプベースの減算回路は、2つの入力電圧の差である出力を生成します。 $V_{1}$ そして $V_{2}$、回路に存在するすべての抵抗が同じ値の場合。
微分や積分などの数学演算を実行する電子回路は、それぞれ微分器と積分器と呼ばれます。
この章では、オペアンプベースについて詳しく説明します differentiatorとインテグレータ。これらもオペアンプの線形アプリケーションに該当することに注意してください。
差別化要因
A differentiator入力の一次導関数に等しい出力を生成する電子回路です。このセクションでは、オペアンプベースの微分器について詳しく説明します。
オペアンプベースの微分器は、その反転端子に印加される入力電圧の差に等しい出力を生成します。ザ・circuit diagram オペアンプベースの微分器の特性を次の図に示します。
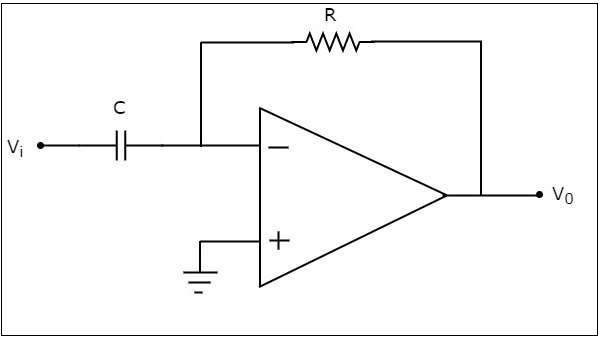
上記の回路では、オペアンプの非反転入力端子はグランドに接続されています。これは、非反転入力端子にゼロボルトが印加されることを意味します。
による virtual short concept、オペアンプの反転入力端子の電圧は、非反転入力端子に存在する電圧と等しくなります。したがって、オペアンプの反転入力端子の電圧はゼロボルトになります。
反転入力端子の節点での節点方程式は次のとおりです。
$$C\frac{\text{d}(0-V_{i})}{\text{d}t}+\frac{0-V_0}{R}=0$$
$$=>-C\frac{\text{d}V_{i}}{\text{d}t}=\frac{V_0}{R}$$
$$=>V_{0}=-RC\frac{\text{d}V_{i}}{\text{d}t}$$
場合 $RC=1\sec$、次に出力電圧 $V_{0}$ −になります
$$V_{0}=-\frac{\text{d}V_{i}}{\text{d}t}$$
したがって、上記のオペアンプベースの微分回路は、入力電圧の差動である出力を生成します。 $V_{i}$、抵抗器とコンデンサのインピーダンスの大きさが互いに逆数である場合。
出力電圧に注意してください $V_{0}$ 持っている negative sign、180が存在することを示す0の入力と出力の間の位相差。
インテグレーター
アン integrator適用された入力の積分である出力を生成する電子回路です。このセクションでは、オペアンプベースの積分器について説明します。
オペアンプベースの積分器は、その反転端子に印加された入力電圧の積分である出力を生成します。ザ・circuit diagram オペアンプベースの積分器の特性を次の図に示します。
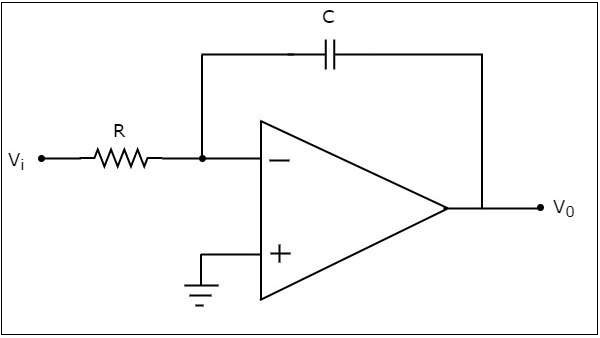
上記の回路では、オペアンプの非反転入力端子はグランドに接続されています。これは、非反転入力端子にゼロボルトが印加されることを意味します。
による virtual short concept、オペアンプの反転入力端子の電圧は、非反転入力端子に存在する電圧と等しくなります。したがって、オペアンプの反転入力端子の電圧はゼロボルトになります。
ザ・ nodal equation 反転入力端子は−です。
$$\frac{0-V_i}{R}+C\frac{\text{d}(0-V_{0})}{\text{d}t}=0$$
$$=>\frac{-V_i}{R}=C\frac{\text{d}V_{0}}{\text{d}t}$$
$$=>\frac{\text{d}V_{0}}{\text{d}t}=-\frac{V_i}{RC}$$
$$=>{d}V_{0}=\left(-\frac{V_i}{RC}\right){\text{d}t}$$
上に示した方程式の両辺を積分すると、次のようになります。
$$\int{d}V_{0}=\int\left(-\frac{V_i}{RC}\right){\text{d}t}$$
$$=>V_{0}=-\frac{1}{RC}\int V_{t}{\text{d}t}$$
場合 $RC=1\sec$、次に出力電圧、 $V_{0}$ −になります
$$V_{0}=-\int V_{i}{\text{d}t}$$
したがって、上記のオペアンプベースの積分回路は、入力電圧の積分である出力を生成します。 $V_{i}$、抵抗器とコンデンサのインピーダンスの大きさが互いに逆数である場合。
Note −出力電圧、 $V_{0}$ 持っている negative sign、180が存在することを示す0の入力と出力の間の位相差。
電圧と電流は基本的な電気量です。要件に応じて、相互に変換できます。Voltage to Current Converter および現在 Voltage Converterこのような変換に役立つ2つの回路です。これらは、オペアンプの線形アプリケーションでもあります。この章では、それらについて詳しく説明します。
電圧-電流変換器
A voltage to current converter または V to I converterは、入力として電流を受け取り、出力として電圧を生成する電子回路です。このセクションでは、オペアンプベースの電圧から電流へのコンバータについて説明します。
オペアンプベースの電圧-電流コンバータは、非反転端子に電圧が印加されると出力電流を生成します。ザ・circuit diagram オペアンプベースの電圧から電流へのコンバータの特性を次の図に示します。
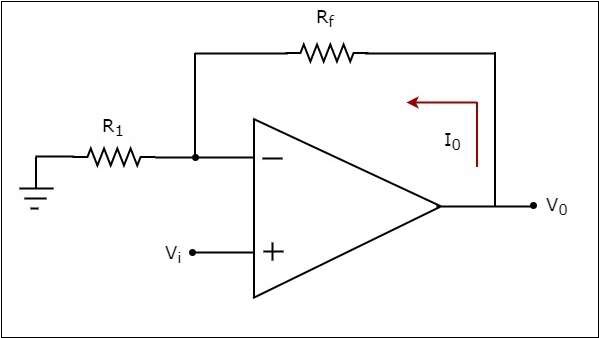
上記の回路では、入力電圧 $V_{i}$オペアンプの非反転入力端子に適用されます。によるvirtual short concept、オペアンプの反転入力端子の電圧は、非反転入力端子の電圧と等しくなります。したがって、オペアンプの反転入力端子の電圧は次のようになります。$V_{i}$。
ザ・ nodal equation 反転入力端子のノードは−です。
$$\frac{V_i}{R_1}-I_{0}=0$$
$$=>I_{0}=\frac{V_t}{R_1}$$
したがって、 output current $I_{0}$ 電圧と電流のコンバーターの比率は、その入力電圧の比率です。 $V_{i}$ と抵抗 $R_{1}$。
上記の式を次のように書き直すことができます。
$$\frac{I_0}{V_i}=\frac{1}{R_1}$$
上記の式は、出力電流の比率を表しています。 $I_{0}$ および入力電圧 $V_{i}$ &それは抵抗の逆数に等しい $R_{1}$ 出力電流の比率 $I_{0}$ および入力電圧 $V_{i}$ と呼ばれる Transconductance。
回路の出力と入力の比率はゲインと呼ばれることがわかっています。したがって、電圧から電流へのコンバータのゲインは相互コンダクタンスであり、抵抗の逆数に等しくなります。$R_{1}$。
電流-電圧変換器
A current to voltage converter または I to V converterは、入力として電流を受け取り、出力として電圧を生成する電子回路です。このセクションでは、オペアンプベースの電流-電圧コンバータについて説明します。
オペアンプベースの電流-電圧コンバータは、その反転端子に電流が印加されると出力電圧を生成します。ザ・circuit diagram オペアンプベースの電流-電圧変換器の特性を次の図に示します。
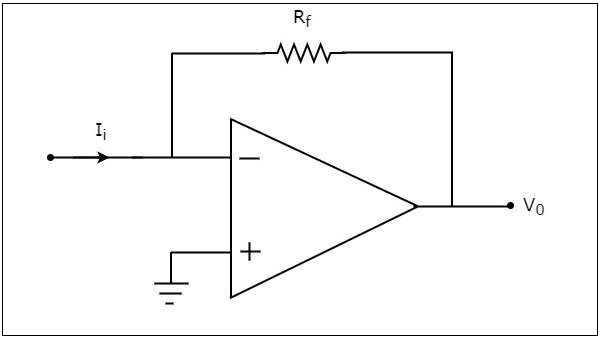
上記の回路では、オペアンプの非反転入力端子はグランドに接続されています。これは、非反転入力端子にゼロボルトが印加されることを意味します。
による virtual short concept、オペアンプの反転入力端子の電圧は、非反転入力端子の電圧と等しくなります。したがって、オペアンプの反転入力端子の電圧はゼロボルトになります。
ザ・ nodal equation 反転端子のノードは−です。
$$-I_{i}+\frac{0-V_0}{R_f}=0$$
$$-I_{i}=\frac{V_0}{R_f}$$
$$V_{0}=-R_{t}I_{i}$$
したがって、 output voltage, $V_{0}$ 電流から電圧への変換器は、フィードバック抵抗の(負の)積です。 $R_{f}$ および入力電流、 $I_{t}$。出力電圧を観察し、$V_{0}$ 持っている negative sign、180が存在することを示す0の入力電流と出力電圧との位相差を。
上記の式を次のように書き直すことができます。
$$\frac{V_0}{I_i}=-R_{f}$$
上記の式は、出力電圧の比率を表しています。 $V_{0}$ および入力電流 $I_{i}$、そしてそれはフィードバック抵抗の負の値に等しい、 $R_{f}$。出力電圧の比率$V_{0}$ および入力電流 $I_{i}$ と呼ばれる Transresistance。
回路の出力と入力の比率は次のように呼ばれることがわかっています。 gain。したがって、電流-電圧コンバータのゲインはそのトランス抵抗であり、(負の)フィードバック抵抗に等しくなります。$R_{f}$ 。
A comparatorは電子回路であり、それに適用される2つの入力を比較し、出力を生成します。コンパレータの出力値は、どちらの入力が大きいか小さいかを示します。コンパレータはICの非線形アプリケーションに該当することに注意してください。
オペアンプは2つの入力端子で構成されているため、オペアンプベースのコンパレータはそれに適用される2つの入力を比較し、比較結果を出力として生成します。この章では、op-amp based comparators。
コンパレータの種類
コンパレータには2つのタイプがあります。 Inverting そして Non-inverting。このセクションでは、これら2つのタイプについて詳しく説明します。
反転コンパレータ
アン inverting comparatorは、リファレンス電圧が非反転端子に印加され、入力電圧が反転端子に印加されるオペアンプベースのコンパレータです。このコンパレータは、inverting 比較する必要のある入力電圧がオペアンプの反転端子に印加されるため、コンパレータ。
ザ・ circuit diagram 反転コンパレータの特性を次の図に示します。
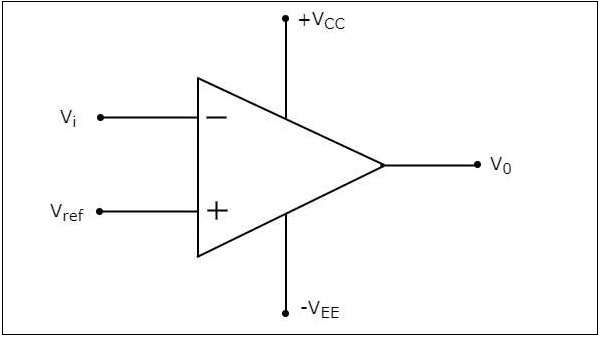
ザ・ operation反転コンパレータの動作は非常に簡単です。2つの値のいずれかを生成します。$+V_{sat}$ そして $-V_{sat}$ 入力電圧の値に基づいて出力で $V_{i}$ および基準電圧 $V_{ref}$。
反転コンパレータの出力値は $-V_{sat}$、その入力 $V_{i}$ 電圧が基準電圧よりも大きい $V_{ref}$。
反転コンパレータの出力値は $+V_{sat}$、その入力 $V_{i}$ 基準電圧よりも低い $V_{ref}$。
例
描いてみましょう output wave form 正弦波入力信号とゼロボルトの基準電圧がそれぞれその反転端子と非反転端子に印加されたときの反転コンパレータの
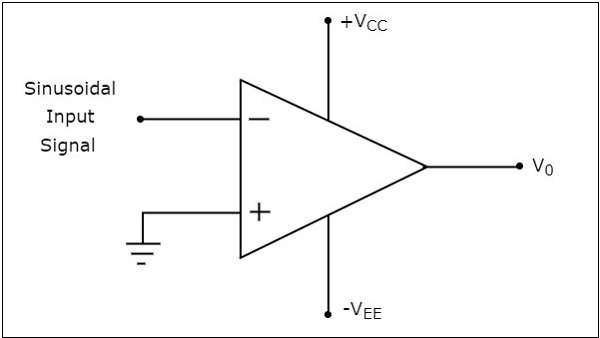
ザ・ operation 上に示した反転コンパレータの概要を以下に説明します。
間に positive half cycle正弦波入力信号の場合、オペアンプの反転端子に存在する電圧はゼロボルトより大きくなります。したがって、反転コンパレータの出力値は次のようになります。$-V_{sat}$ 正弦波入力信号の正の半サイクル中。
同様に、 negative half cycle正弦波入力信号の場合、オペアンプの反転端子に存在する電圧はゼロボルト未満です。したがって、反転コンパレータの出力値は次のようになります。$+V_{sat}$ 正弦波入力信号の負の半サイクル中。
次の図は、 input and output waveforms 基準電圧がゼロボルトの場合の反転コンパレータの
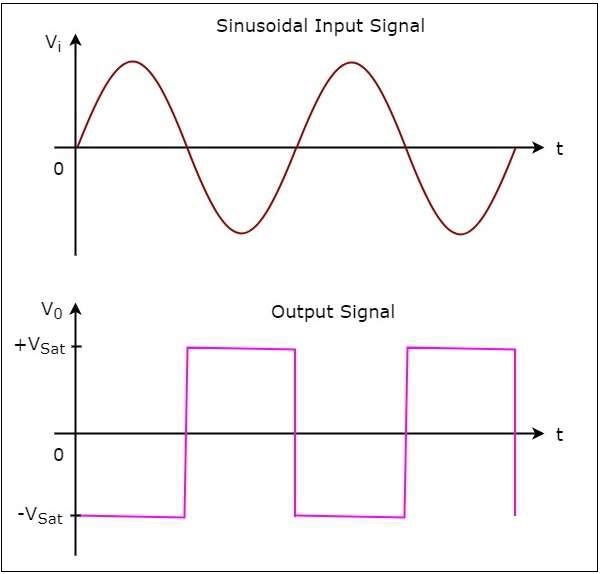
上に示した図では、出力が次のいずれかから遷移することがわかります。 $-V_{sat}$ に $+V_{sat}$ またはから $+V_{sat}$ に $-V_{sat}$正弦波入力信号がゼロボルトを超えているときはいつでも。つまり、入力がゼロボルトを超えると、出力の値が変化します。したがって、上記の回路は次のようにも呼ばれます。inverting zero crossing detector.
非反転コンパレータ
非反転コンパレータは、リファレンス電圧がその反転端子に印加され、入力電圧がその非反転端子に印加されるオペアンプベースのコンパレータです。このオペアンプベースのコンパレータは、non-inverting 比較する必要のある入力電圧がオペアンプの非反転端子に印加されるため、コンパレータ。
ザ・ circuit diagram 非反転コンパレータの特性を次の図に示します。
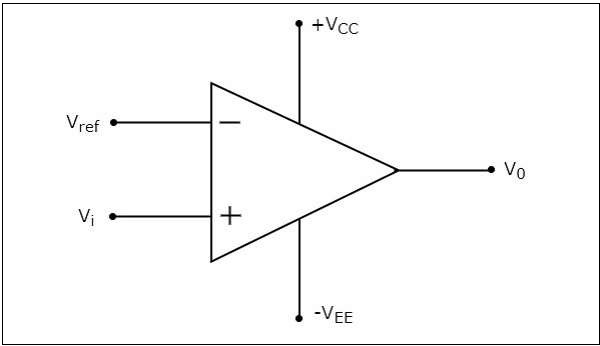
ザ・ operation非反転コンパレータの開発は非常に簡単です。2つの値のいずれかを生成します。$+V_{sat}$ そして $-V_{sat}$ 入力電圧の値に基づいて出力で $V_{t}$ および基準電圧 $+V_{ref}$。
非反転コンパレータの出力値は次のようになります。 $+V_{sat}$、入力電圧 $V_{i}$ 基準電圧よりも大きい $+V_{ref}$。
非反転コンパレータの出力値はハチになります $-V_{sat}$、入力電圧 $V_{i}$ 基準電圧よりも低い $+V_{ref}$。
例
描いてみましょう output wave form 正弦波入力信号とゼロボルトの基準電圧がそれぞれオペアンプの非反転端子と反転端子に印加されたときの非反転コンパレータの特性。
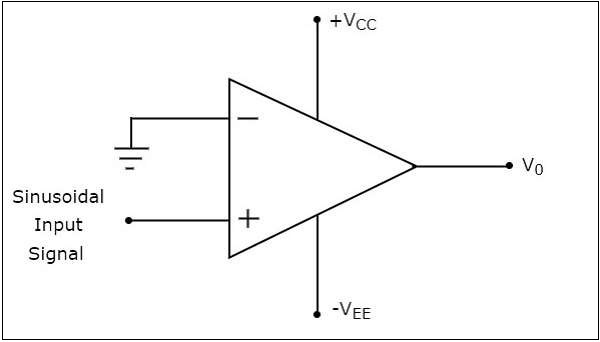
ザ・ operation 非反転コンパレータの特性を以下に説明します-
間に positive half cycle正弦波入力信号の場合、オペアンプの非反転端子に存在する電圧はゼロボルトより大きくなります。したがって、非反転コンパレータの出力値は次のようになります。$+V_{sat}$ 正弦波入力信号の正の半サイクル中。
同様に、 negative half cycle正弦波入力信号の場合、オペアンプの非反転端子に存在する電圧はゼロボルト未満です。したがって、非反転コンパレータの出力値は次のようになります。$-V_{sat}$ 正弦波入力信号の負の半サイクル中。
次の図は、 input and output waveforms 基準電圧がゼロボルトの場合の非反転コンパレータの
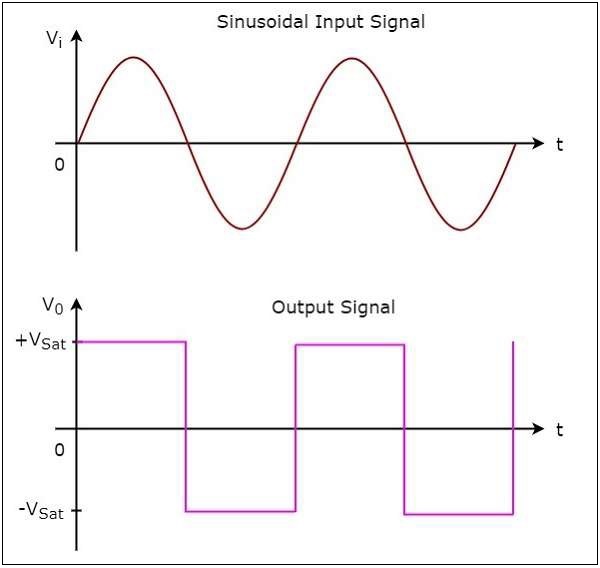
上に示した図から、出力が次のいずれかから遷移することがわかります。 $+V_{sat}$ に $-V_{sat}$ またはから $-V_{sat}$ に $+V_{sat}$正弦波入力信号がゼロボルトを超えるときはいつでも。つまり、入力がゼロボルトを超えると、出力の値が変化します。したがって、上記の回路は次のようにも呼ばれます。non-inverting zero crossing detector。
対数や真数(指数関数)などの数学演算を増幅して行う電子回路を次のように呼びます。 Logarithmic amplifier そして Anti-Logarithmic amplifier それぞれ。
この章では、 Logarithmic amplifier そして Anti-Logarithmic amplifier詳細に。これらのアンプは非線形アプリケーションに該当することに注意してください。
対数増幅器
A logarithmic amplifier、または log amplifierは、適用された入力の対数に比例する出力を生成する電子回路です。このセクションでは、オペアンプベースの対数増幅器について詳しく説明します。
オペアンプベースの対数増幅器は、出力に電圧を生成します。これは、反転端子に接続された抵抗に印加される電圧の対数に比例します。ザ・circuit diagram オペアンプベースの対数増幅器の特性を次の図に示します。
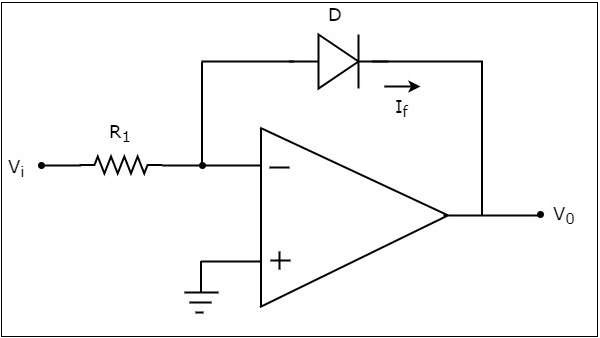
上記の回路では、オペアンプの非反転入力端子はグランドに接続されています。これは、オペアンプの非反転入力端子にゼロボルトが印加されることを意味します。
による virtual short concept、オペアンプの反転入力端子の電圧は、非反転入力端子の電圧と等しくなります。したがって、反転入力端子の電圧はゼロボルトになります。
ザ・ nodal equation 反転入力端子のノードは−です。
$$\frac{0-V_i}{R_1}+I_{f}=0$$
$$=>I_{f}=\frac{V_i}{R_1}......Equation 1$$
以下は equation for current 順方向バイアスの場合、ダイオードを流れる-
$$I_{f}=I_{s} e^{(\frac{V_f}{nV_T})} ......Equation 2$$
どこ、
$I_{s}$ はダイオードの飽和電流です。
$V_{f}$ は、順方向バイアスの場合のダイオード両端の電圧降下です。
$V_{T}$ はダイオードの熱等価電圧です。
ザ・ KVL equation オペアンプのフィードバックループの周りは次のようになります-
$$0-V_{f}-V_{0}=0$$
$$=>V_{f}=-V_{0}$$
の値を代入する $V_{f}$ 式2では、次のようになります。
$$I_{f}=I_{s} e^{\left(\frac{-V_0}{nV_T}\right)} ......Equation 3$$
式1と式3の両方の左側の項が同じであることに注意してください。したがって、以下に示すように、これら2つの方程式の右辺の項を等しくします。
$$\frac{V_i}{R_1}=I_{s}e^{\left(\frac{-V_0}{nV_T}\right)}$$
$$\frac{V_i}{R_1I_s}= e^{\left(\frac{-V_0}{nV_T}\right)}$$
申請中 natural logarithm 両側で、次のようになります。
$$In\left(\frac{V_i}{R_1I_s}\right)= \frac{-V_0}{nV_T}$$
$$V_{0}=-{nV_T}In\left(\frac{V_i}{R_1I_s}\right)$$
上記の式では、パラメータn、 ${V_T}$ そして $I_{s}$定数です。だから、出力電圧$V_{0}$ に比例します natural logarithm 入力電圧の $V_{i}$ 抵抗の固定値の場合 $R_{1}$。
したがって、上記のオペアンプベースの対数増幅器回路は、入力電圧の自然対数に比例する出力を生成します。 ${V_T}$、 いつ ${R_1I_s}=1V$。
出力電圧に注意してください $V_{0}$ があります negative sign、180が存在することを示す0の入力と出力の間の位相差。
反対数増幅器
アン anti-logarithmic amplifier、または anti-log amplifierは、適用された入力の真数に比例する出力を生成する電子回路です。このセクションでは、オペアンプベースの反対数増幅器について詳しく説明します。
オペアンプベースの反対数増幅器は、出力に電圧を生成します。これは、反転端子に接続されたダイオードに印加される電圧の反対数に比例します。
ザ・ circuit diagram オペアンプベースの反対数増幅器の特性を次の図に示します。

上記の回路では、オペアンプの非反転入力端子はグランドに接続されています。これは、非反転入力端子にゼロボルトが印加されていることを意味します。
による virtual short concept、オペアンプの反転入力端子の電圧は、非反転入力端子に存在する電圧と等しくなります。したがって、その反転入力端子の電圧はゼロボルトになります。
ザ・ nodal equation 反転入力端子のノードは−です。
$$-I_{f}+\frac{0-V_0}{R_f}=0$$
$$=>-\frac{V_0}{R_f}=I_{f}$$
$$=>V_{0}=-R_{f}I_{f}.........Equation 4$$
ダイオードが順方向バイアスされているときにダイオードを流れる電流の式は、次のようになります。
$$I_{f}=I_{s} e^{\left(\frac{V_f}{nV_T}\right)}$$
の値を代入する $I_{f}$ 式4では、次のようになります。
$$V_{0}=-R_{f}\left \{{I_{s} e^{\left(\frac{V_f}{nV_T}\right)}}\right \}$$
$$V_{0}=-R_{f}{I_{s} e^{\left(\frac{V_f}{nV_T}\right)}}......Equation 5$$
オペアンプの反転端子の入力側のKVL式は次のようになります。
$$V_{i}-V_{f}=0$$
$$V_{f}=V_{i}$$
式5のの値を代入すると、次のようになります。
$$V_{0}=-R_{f}{I_{s} e^{\left(\frac{V_i}{nV_T}\right)}}$$
上記の式では、パラメータn、 ${V_T}$ そして $I_{s}$定数です。だから、出力電圧${V_0}$ に比例します anti-natural logarithm 入力電圧の(指数関数的) ${V_i}$、フィードバック抵抗の固定値の場合 ${R_f}$。
したがって、上記のオペアンプベースの反対数増幅器回路は、入力電圧の反自然対数(指数)に比例する出力を生成します。 ${V_i}$ いつ、 ${R_fI_s}= 1V$。出力電圧に注意してください${V_0}$ 持っている negative sign、180が存在することを示す0の入力と出力の間の位相差。
AC そして DC 電荷の流れを研究するときに遭遇する2つのよくある用語です。 Alternating Current (AC)状態を継続的に変更するプロパティがあります。たとえば、正弦波を考えると、電流は正の半サイクルでは一方向に流れ、負の半サイクルでは反対方向に流れます。一方、Direct Current (DC) 一方向にのみ流れます。
AC信号が印加されたときにDC信号または脈動DC信号のいずれかを生成する電子回路は、 rectifier。この章では、オペアンプベースの整流器について詳しく説明します。
整流器の種類
整流器は2つのタイプに分類されます。 Half wave rectifier そして Full wave rectifier。このセクションでは、これら2つのタイプについて詳しく説明します。
半波整流器
A half wave rectifier は、入力の半サイクルで出力に正の半サイクルを生成し、入力の残りの半サイクルでゼロ出力を生成する整流器です。
ザ・ circuit diagram 次の図に、半波整流器の特性を示します。

二つのダイオードDと、反転増幅器のように見える上に示した半波整流器の回路図ことを観察1及びD 2に加えました。
ザ・ working 上記の半波整流回路の概要を以下に説明します。
のために positive half cycle正弦波入力の場合、オペアンプの出力は負になります。従って、ダイオードD 1は順方向バイアスされます。
ダイオードDときに1が順バイアスである、オペアンプの出力電圧があろう-0.7 V.したがって、ダイオードD 2が逆バイアスされます。従ってoutput voltage 上記の回路の zero ボルト。
したがって、 no (zero) output 正弦波入力の正の半サイクルのための半波整流器の。
のために negative half cycle正弦波入力の場合、オペアンプの出力は正になります。従って、ダイオードD 1及びD 2が逆バイアスされ、順方向バイアスされ、それぞれ。したがって、上記の回路の出力電圧は次のようになります。
$$V_0=-\left(\frac{R_f}{R_1}\right)V_1$$
したがって、半波整流器の出力は次のようになります。 positive half cycle 正弦波入力の負の半サイクルの場合。
波形
ザ・ input そして output waveforms 半波整流器の概要を次の図に示します。

上のグラフからわかるように、説明した半波整流回路図は次のようになります。 positive half cycles 正弦波入力の負の半サイクルの場合、正弦波入力の正の半サイクルの場合はゼロ出力
全波整流器
A full wave rectifier 入力の両方の半サイクルについて、出力で正の半サイクルを生成します。
ザ・ circuit diagram 全波整流器の概要を次の図に示します。
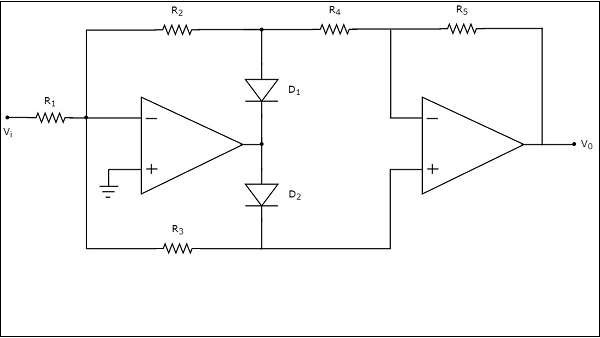
上記の回路図は、2つのオペアンプ、二つのダイオード、Dから成る1&D 2及び5の抵抗、R 1 Rに対して5。ザ・working 上記の全波整流回路の概要を以下に説明します。
のために positive half cycle正弦波入力の場合、最初のオペアンプの出力は負になります。したがって、ダイオードD 1及びD 2が順バイアスされ、それぞれ逆バイアス。
この場合、最初のオペアンプの出力電圧は次のようになります。
$$V_{01}=-\left(\frac{R_2}{R_1}\right)V_i$$
最初のオペアンプの出力が抵抗Rに接続されていることを観察する4第二オペアンプの反転端子に接続されています、。第二オペアンプの非反転端子の電圧存在は0 V.そこで、抵抗を有する第二のオペアンプであり、R 4及びR 4つのANとして作用inverting amplifier。
2番目のオペアンプの出力電圧は次のようになります。
$$V_0=-\left(\frac{R_5}{R_4}\right)V_{01}$$
Substituting の値 $V_{01}$ 上記の式では、次のようになります。
$$=>V_{0}=-\left(\frac{R_5}{R_4}\right)\left \{ -\left(\frac{R_2}{R_1}\right)V_{i} \right \}$$
$$=>V_{0}=\left(\frac{R_2R_5}{R_1R_4}\right)V_{i}$$
したがって、全波整流器の出力は、正の半サイクルになります。 positive half cycle正弦波入力の。この場合、出力のゲインは次のようになります。$\frac{R_2R_5}{R_1R_4}$。考えれば$R_{1}=R_{2}=R_{4}=R_{5}=R$の場合、出力のゲインは1になります。
のために negative half cycle正弦波入力の場合、最初のオペアンプの出力は正になります。したがって、ダイオードD 1及びD 2は逆バイアスとフォワードそれぞれバイアスされます。
最初のオペアンプの出力電圧は-になります
$$V_{01}=-\left(\frac{R_3}{R_1}\right)V_{i}$$
最初のオペアンプの出力は、2番目のオペアンプの非反転端子に直接接続されています。今、抵抗を有する第二のオペアンプ、R 4及びR 5つのAのように作用しますnon-inverting amplifier。
2番目のオペアンプの出力電圧は-になります
$$V_{0}=\left(1+\frac{R_5}{R_4}\right)V_{01}$$
Substituting の値 $V_{01}$ 上記の式では、次のようになります。
$$=>V_{0}=\left(1+\frac{R_5}{R_4}\right) \left\{-\left(\frac{R_3}{R_1}\right)V_{i}\right \} $$
$$=>V_{0}=-\left(\frac{R_3}{R_1}\right)\left(1+\frac{R_5}{R_4}\right)V_{i}$$
したがって、全波整流器の出力は次のようになります。 positive half cycle正弦波入力の負の半サイクルについても同様です。この場合、出力のゲインの大きさは次のようになります。$\left(\frac{R_3}{R_1}\right)\left(1+\frac{R_5}{R_4}\right)$。考えれば$R_{1}=2R_{3}=R_{4}=R_{5}=R$ その場合、出力のゲインは次のようになります。 one。
ザ・ input そして output waveforms 全波整流器の概要を次の図に示します。
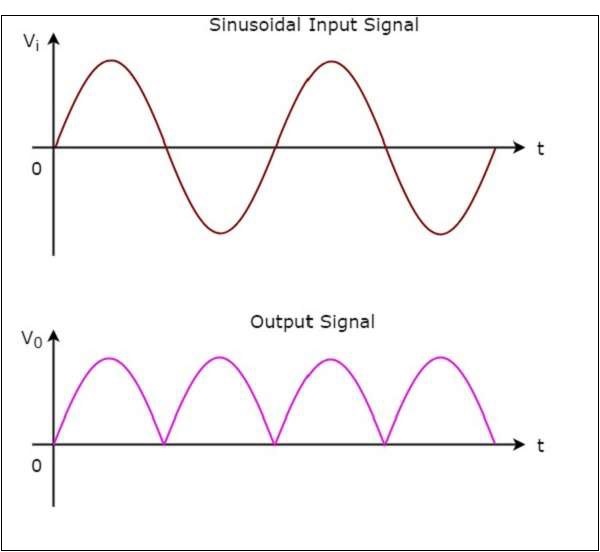
上の図でわかるように、私たちが検討した全波整流回路図は、 positive half cycles 正弦波入力の正と負の両方の半サイクル。
Wave shaping circuitsは電子回路であり、適用された入力波形からの出力で目的の形状を生成します。これらの回路は2つの機能を実行します-
- 加えられた波を減衰させる
- 適用される波のDCレベルを変更します。
波形整形回路には2つのタイプがあります。 Clippers そして Clampers。この章では、クリッパーについて詳しく学習します。
オペアンプベースのクリッパー
A clipperは、基準値より上または下の入力の一部を除去することによって出力を生成する電子回路です。つまり、クリッパーの出力は、クリップされた部分以外の入力の出力と同じになります。このため、クリッパーの出力のピークツーピーク振幅は常に入力の振幅よりも小さくなります。
クリッパーの主な利点は、AC信号の振幅に存在する不要なノイズを排除することです。
クリッパーは、入力のクリッピング部分に基づいて、次の2つのタイプに分類できます。
- ポジティブクリッパー
- ネガティブクリッパー
これらについては、以下のように詳細に説明します。
ポジティブクリッパー
A positive clipper 入力信号の正の部分のみをクリップするクリッパーです。
ザ・ circuit diagramポジティブクリッパーの割合を次の図に示します-
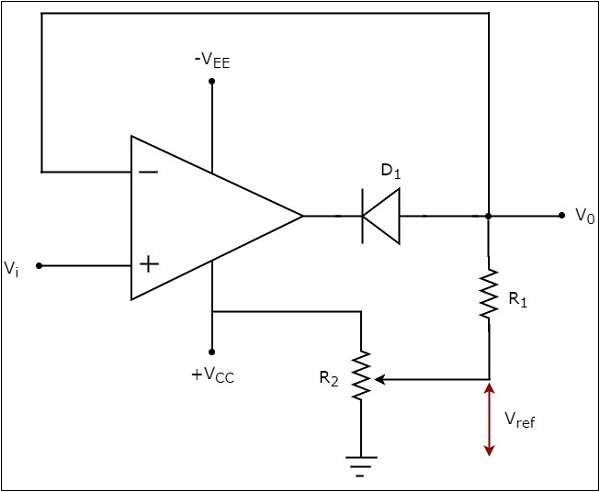
上記の回路では、正弦波電圧信号 $V_{t}$オペアンプの非反転端子に適用されます。基準電圧の値$V_{ref}$ 抵抗を変えることで選択できます $R_{2}$。
ザ・ operation 上記の回路の概要を以下に説明します-
入力電圧の値が $V_i$ 基準電圧の値よりも小さい $V_{ref}$、次にダイオードD1が導通する。次に、上記の回路は次のように動作します。voltage follower。したがって、出力電圧$V_{0}$ 上記の回路のそれは入力電圧のそれと同じになります $V_{i}$、 にとって $V_{i}$ < $V_{ref}$。
入力電圧の値が $V_{i}$ 基準電圧の値よりも大きい $V_{ref}$、その後、ダイオードD 1がオフになります。これで、フィードバックパスが開いていたため、オペアンプは開ループで動作します。したがって、出力電圧$V_{0}$ 上記の回路の値は基準電圧の値に等しくなります $V_{ref}$、 にとって $V_{i}$ >> $V_{ref}$。
ザ・ input wave form および対応する output wave form 正の基準電圧に対する正のクリッパーの $V_{ref}$、を次の図に示します-
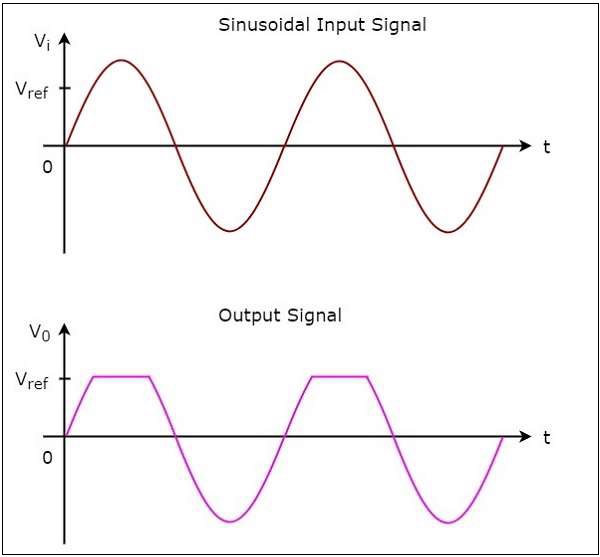
ネガティブクリッパー
A negative clipper入力信号の負の部分のみをクリップするクリッパーです。正のクリッパーで見た回路で、ダイオードを逆にして基準電圧の逆極性をとるだけで、負のクリッパーの回路を得ることができます。
ザ・ circuit diagram ネガティブクリッパーの例を次の図に示します-
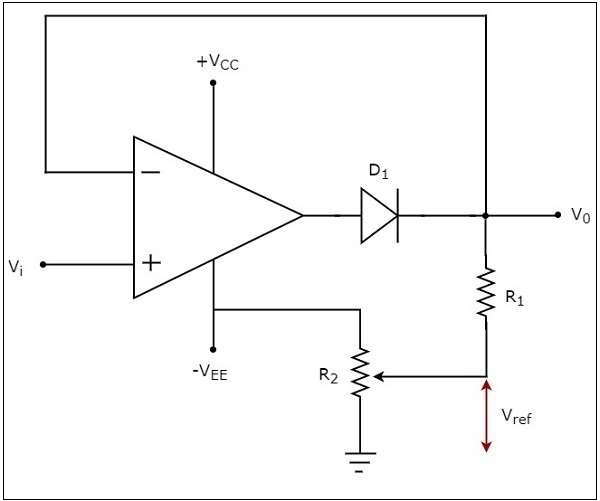
上記の回路では、正弦波電圧信号 $V_{i}$オペアンプの非反転端子に適用されます。基準電圧の値$V_{ref}$ 抵抗を変えることで選択できます $R_{2}$。
ザ・ operation ネガティブクリッパー回路の概要を以下に説明します−
入力電圧の値が $V_{t}$ 基準電圧の値よりも大きい $V_{ref}$、次にダイオードD1が導通する。すると、上記の回路は次のように動作します。voltage follower。したがって、出力電圧$V_{0}$ 上記の回路のそれは入力電圧のそれと同じになります $V_{i}$ にとって $V_{i}$> $V_{ref}$。
入力電圧の値が $V_{i}$以下の基準電圧の値より、次にダイオードD 1がオフになります。これで、フィードバックパスが開いているため、オペアンプは開ループで動作します。したがって、出力電圧$V_{0}$ 上記の回路の値は基準電圧の値に等しくなります、$V_{ref}$ にとって $V_{i}$ < $V_{ref}$。
ザ・ input wave form および対応する output wave form 負の基準電圧の場合、負のクリッパーの $V_{ref}$、を次の図に示します-
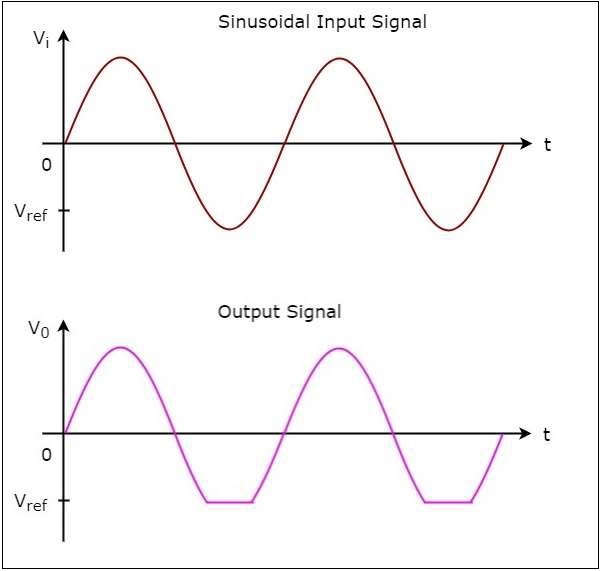
前の章では、クリッパーについて説明しました。それでは、他のタイプの波形整形回路、つまりクランパーについて説明しましょう。
オペアンプベースのクランパー
A clamperは出力を生成する電子回路です。これは入力と似ていますが、DCレベルがシフトしています。言い換えると、クランパーの出力は入力の正確なレプリカです。したがって、クランパーの出力のピークツーピーク振幅は、常に入力の振幅と等しくなります。
クランパーは、出力で入力信号のDCレベルを導入または復元するために使用されます。があるtwo types 入力のDCシフトに基づくオペアンプベースのクランパーの特性。
- ポジティブクランパー
- ネガティブクランパー
このセクションでは、これら2種類のクランパーについて詳しく説明します。
ポジティブクランパー
正のクランパーは、入力信号が正のDC値だけ垂直方向にシフトするように出力を生成するクランパー回路です。
ザ・ circuit diagram ポジティブクランパーの特性を次の図に示します。
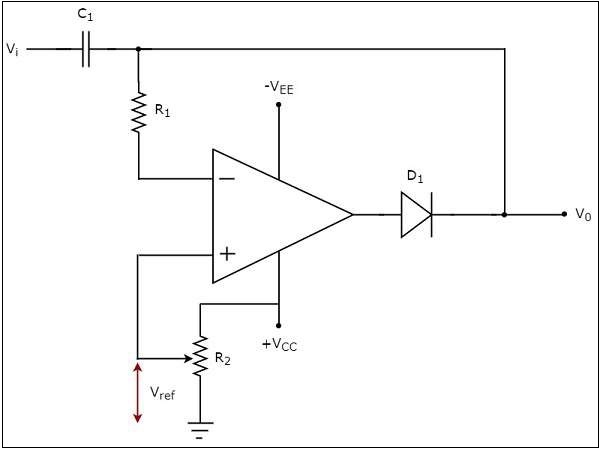
上記の回路では、 sinusoidal voltage signal、 $V_{i}$ コンデンサで構成されるネットワークを介してオペアンプの反転端子に適用されます $C_{1}$ と抵抗器 $R_{1}$。つまり、AC電圧信号がオペアンプの反転端子に印加されます。
ザ・ DC reference voltage $V_{ref}$ オペアンプの非反転端子に適用されます。基準電圧の値$V_{ref}$ 抵抗を変えることで選択できます $R_{2}$。この場合、基準電圧を取得します$V_{ref}$ 正の値の。
上記の回路は output, これ is the combination (resultant sum) 正弦波電圧信号の $V_{i}$ および基準電圧 $V_{ref}$。つまり、クランパー回路は、正弦波電圧信号が次のように出力を生成します。$V_{i}$ 基準電圧の値だけ垂直上向きにシフトします $V_{ref}$。
ポジティブクランパーの入力波形と対応する出力波形を上の図に示します。
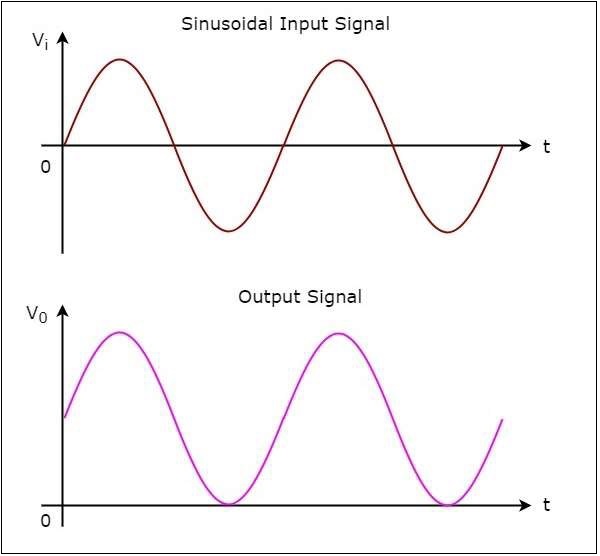
上の図から、正のクランパーが適用された入力波形をシフトすることがわかります。 vertically upward出力で。シフト量は、DCリファレンス電圧の値によって異なります。
ネガティブクランパー
A negative clamper は、入力信号が負のDC値だけ垂直方向にシフトするように出力を生成するクランパー回路です。
ザ・ circuit diagram ネガティブクランパーの概要を次の図に示します。
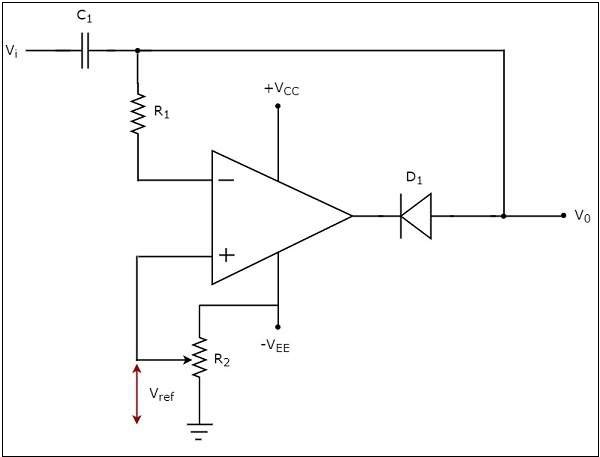
上記の回路では、 sinusoidal voltage signal $V_{i}$ コンデンサCから構成され、ネットワークを介してオペアンプの反転端子に印加され、1と抵抗$R_{1}$。つまり、AC電圧信号がオペアンプの反転端子に印加されます。
ザ・ DC reference voltage $V_{ref}$ オペアンプの非反転端子に印加されます。基準電圧の値 $V_{ref}$ 抵抗を変えることで選択できます $R_{2}$。この場合、基準電圧を取得します$V_{ref}$ 負の値の。
上記の回路は、正弦波電圧信号の組み合わせ(結果の合計)である出力を生成します $V_{i}$ および基準電圧 $V_{ref}$。つまり、クランパー回路は、正弦波電圧信号が次のように出力を生成します。$V_{i}$ 基準電圧の値だけ垂直下向きにシフトします $V_{ref}$。
ネガティブクランパーの入力波形と対応する出力波形を次の図に示します。
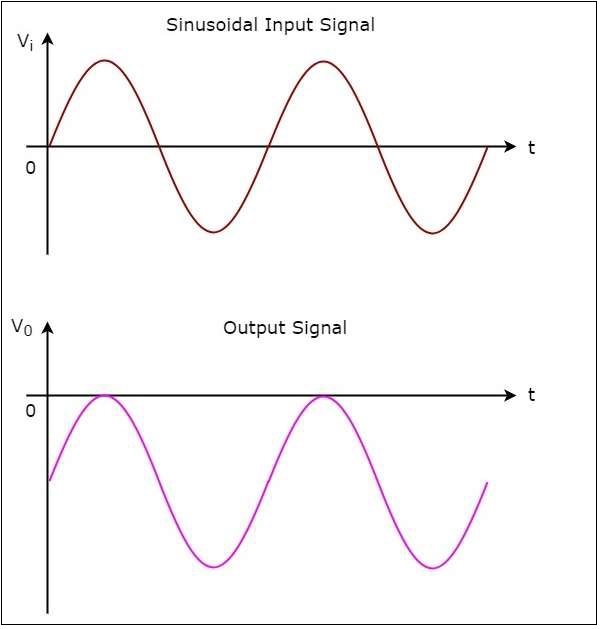
出力から、負のクランパーが適用された入力波形をシフトすることがわかります。 vertically downward出力で。シフト量は、DCリファレンス電圧の値によって異なります。
Filters特定の周波数成分を許可したり、他の成分を拒否したりする電子回路です。ネットワーク理論のチュートリアルでフィルターに出くわしたかもしれません。それらは受動的であり、抵抗器、コンデンサ、および(または)インダクタなどの受動要素で構成される電気回路またはネットワークです。
この章では、 active filters 詳細に。
アクティブフィルターの種類
アクティブフィルタは電子回路であり、オペアンプなどのアクティブ要素と、抵抗やコンデンサなどのパッシブ要素で構成されています。
アクティブフィルターは主に以下に分類されます four types 彼らが許可および/または拒否している周波数の帯域に基づいて-
- アクティブローパスフィルター
- アクティブハイパスフィルター
- アクティブバンドパスフィルター
- アクティブバンドストップフィルター
アクティブローパスフィルター
アクティブなフィルターが許可(パス)のみを許可する場合 low frequency コンポーネントと他のすべての高周波コンポーネントを拒否(ブロック)し、それからそれはと呼ばれます active low pass filter。
ザ・ circuit diagram アクティブローパスフィルターの特性を次の図に示します。
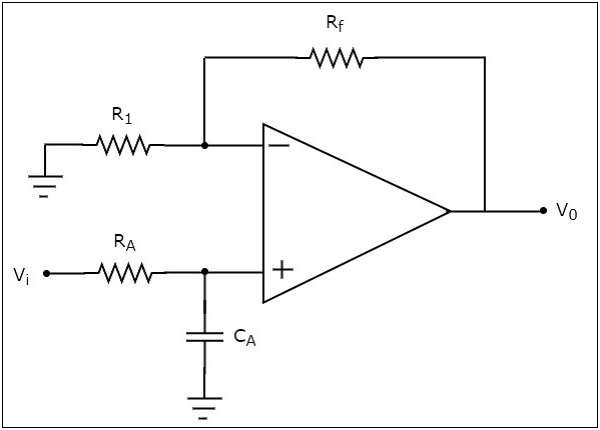
オペアンプの非反転端子に接続されている電気ネットワークは、 passive low pass filter。したがって、オペアンプの非反転端子の入力は、パッシブローパスフィルタの出力です。
上記の回路が次のようになっていることを確認してください。 non-inverting amplifier。オペアンプの非反転端子への入力としてパッシブローパスフィルタの出力を持っています。したがって、次のような出力が生成されます。$\left(1+\frac{R_f}{R_1}\right)$ 非反転端子に存在する入力の倍。
の値を選択できます $R_{f}$ そして $R_{1}$ 適切に取得するために desired gain出力で。の抵抗値を考慮すると、$R_{f}$ そして $R_{1}$ ゼロオームと無限オームとして、上記の回路は unity gain ローパスフィルター出力。
アクティブハイパスフィルター
アクティブなフィルターが許可(パス)のみを許可する場合 high frequency コンポーネントと他のすべての低周波コンポーネントを拒否(ブロック)し、それはと呼ばれます active high pass filter。
ザ・ circuit diagram アクティブハイパスフィルターの特性を次の図に示します。
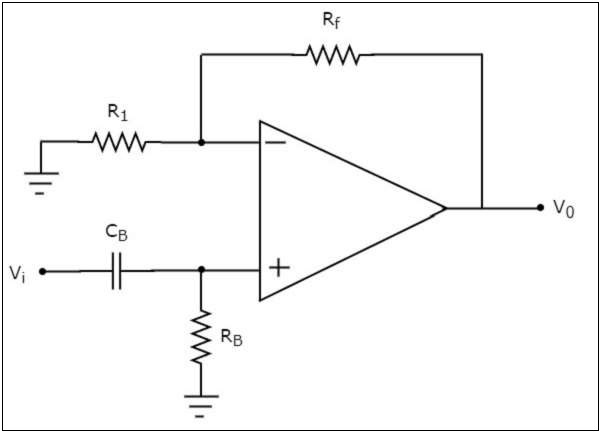
オペアンプの非反転端子に接続されている電気ネットワークは、 passive high pass filter。したがって、オペアンプの非反転端子の入力は、パッシブハイパスフィルタの出力です。
さて、上記の回路は non-inverting amplifier。オペアンプの非反転端子への入力としてパッシブハイパスフィルターの出力を持っています。したがって、次のような出力が生成されます。$\left(1+\frac{R_f}{R_1}\right)$ 非反転端子に存在する入力の倍。
の値を選択できます $R_f$ そして $R_1$ 適切に取得するために desired gain出力で。の抵抗値を考慮すると、$R_{f}$ そして $R_{1}$ ゼロオームと無限オームとして、上記の回路は unity gain ハイパスフィルター出力。
アクティブバンドパスフィルター
アクティブフィルターが1つの周波数帯域のみを許可(通過)する場合、それは active band pass filter。一般に、この周波数帯域は低周波数範囲と高周波数範囲の間にあります。したがって、アクティブバンドパスフィルターは、低周波数成分と高周波数成分の両方を拒否(ブロック)します。
ザ・ circuit diagram アクティブバンドパスフィルターの概要を次の図に示します。
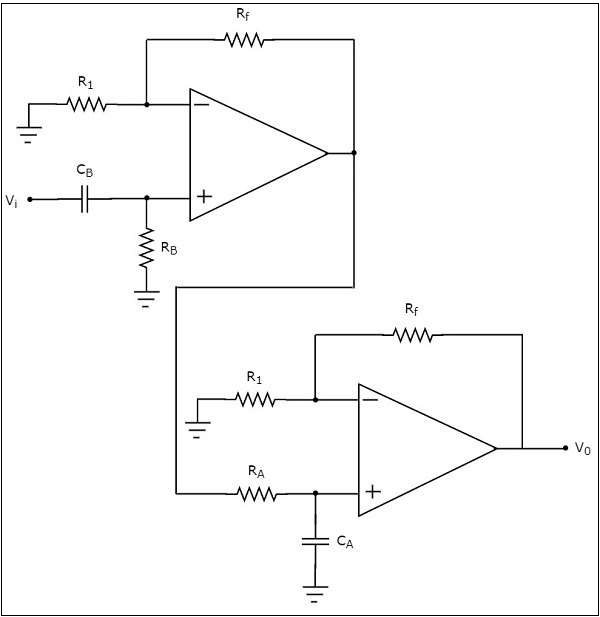
あることに注意してください two parts アクティブバンドパスフィルターの回路図:最初の部分はアクティブハイパスフィルターで、2番目の部分はアクティブローパスフィルターです。
アクティブハイパスフィルターの出力は、アクティブローパスフィルターの入力として適用されます。つまり、アクティブハイパスフィルターとアクティブローパスフィルターの両方が cascaded 特定の周波数帯域のみを含むように出力を取得するため。
ザ・ active high pass filter、は最初の段階に存在し、より高い周波数を許可します lower cut-off frequencyアクティブバンドパスフィルターの。したがって、の値を選択する必要があります$R_{B}$ そして $C_{B}$ 適切に、望ましいを得るために lower cut-off frequency アクティブバンドパスフィルターの。
同様に、 active low pass filterは、第2ステージに存在し、アクティブバンドパスフィルターのより高いカットオフ周波数よりも小さい周波数を許可します。したがって、の値を選択する必要があります$R_{A}$ そして $C_{A}$ 適切に望ましいを得るために higher cut-off frequency アクティブバンドパスフィルターの。
したがって、上記の図の回路は、アクティブバンドパスフィルター出力を生成します。
アクティブバンドストップフィルター
アクティブフィルターが特定の周波数帯域を拒否(ブロック)する場合、それは active band stop filter。一般に、この周波数帯域は低周波数範囲と高周波数範囲の間にあります。したがって、アクティブバンドストップフィルターは、低周波数成分と高周波数成分の両方を許可(通過)します。
ザ・ block diagram アクティブバンドストップフィルターの特性を次の図に示します。
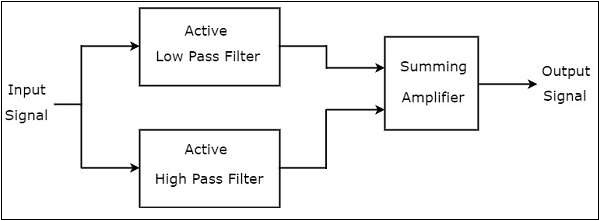
アクティブバンドストップフィルターのブロック図は、最初の段階でアクティブローパスフィルターとアクティブハイパスフィルターの2つのブロックで構成されていることに注意してください。これらの2つのブロックの出力は、第2ステージに存在するブロックへの入力として適用されます。だから、summing amplifier 出力を生成します。これは、アクティブローパスフィルターとアクティブハイパスフィルターの出力の合計を増幅したものです。
したがって、上記のブロック図の出力は次のようになります。 output of an active band stop 、ローパスフィルターのカットオフ周波数をハイパスフィルターのカットオフ周波数よりも小さく選択した場合。
ザ・ circuit diagram アクティブバンドストップフィルターの特性を次の図に示します。

アクティブローパスフィルタ、アクティブハイパスフィルタ、および加算増幅器の回路図はすでに見てきました。上記を取得したことを確認してくださいcircuit diagram アクティブバンドストップフィルターのブロック図のそれぞれの回路図でブロックを置き換えることにより、アクティブバンドストップフィルターを作成します。
発振器は、周期的な信号を生成する電子回路です。発振器が正弦波振動を生成する場合、それはと呼ばれますsinusoidal oscillator。DC電源からの入力エネルギーを周期信号のAC出力エネルギーに変換します。この周期的な信号は、特定の周波数と振幅を持ちます。
ザ・ block diagram 正弦波発振器の特性を次の図に示します-
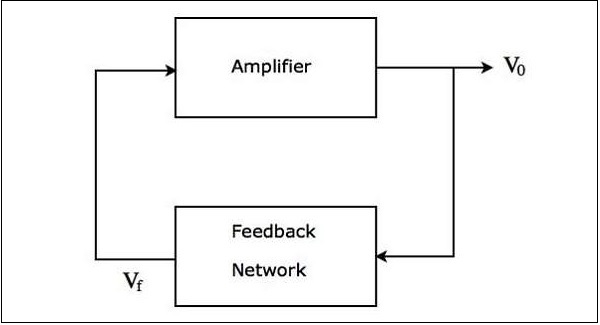
上の図は主に two blocks:増幅器とフィードバックネットワーク。フィードバックネットワークは、増幅器への入力として増幅器の出力の一部を取り、電圧信号を生成します。この電圧信号は、アンプへの入力として適用されます。
上に示した正弦波発振器のブロック図は、次の場合に正弦波振動を生成します。 two conditions 満足している−
ザ・ loop gain $A_{v}\beta$ 正弦波発振器の上記のブロック図のは、以上でなければなりません unity。ここに、$A_{v}$ そして $\beta$ はそれぞれ増幅器のゲインとフィードバックネットワークのゲインです。
合計 phase shift 正弦波発振器の上記のブロック図のループの周りは、次のいずれかである必要があります。 00 または 3600。
上記の2つの条件を合わせて次のように呼びます。 Barkhausen criteria。
オペアンプベースのオシレータ
がある two オペアンプベースのオシレータのタイプ。
- RC位相シフト発振器
- ウィーンブリッジ発振器
このセクションでは、それぞれについて詳しく説明します。
RC位相シフト発振器
反転増幅器とフィードバックネットワークの助けを借りて出力に正弦波電圧信号を生成するオペアンプベースの発振器は、 RC phase shift oscillator。このフィードバックネットワークは、3つのカスケードされたRCセクションで構成されています。
ザ・ circuit diagram RC位相シフト発振器の概要を次の図に示します。
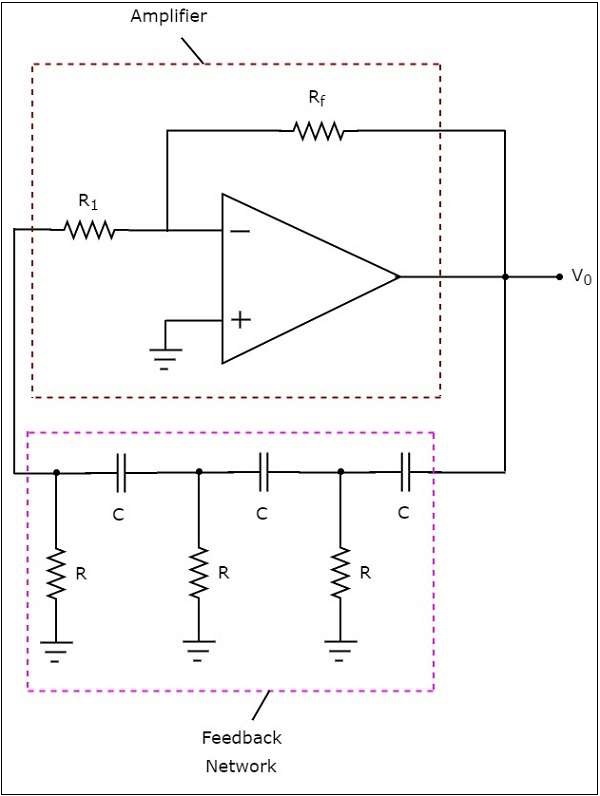
上記の回路では、オペアンプは inverting mode。したがって、180の位相シフトを提供0。上記回路の帰還ネットワークの存在はまた、180の位相シフトを提供0を各RC部60の位相シフトを提供するので、0。従って、上記回路360の全位相シフト提供0いくつかの周波数です。
ザ・ output frequency RC位相シフト発振器のは−
$$f=\frac{1}{2\Pi RC\sqrt[]{6}}$$
ザ・ gain $A_{v}$ 反転増幅器のは-29以上である必要があります。
$$i.e.,-\frac{R_f}{R_1}\geq-29$$
$$=>\frac{R_f}{R_1}\geq-29$$
$$=>R_{f}\geq29R_{1}$$
したがって、フィードバック抵抗の値を考慮する必要があります $R_{f}$、抵抗器の値の最低29倍 $R_{1}$、RC位相シフト発振器の出力で持続的な発振を生成するため。
ウィーンブリッジ発振器
非反転増幅器とフィードバックネットワークの助けを借りて出力に正弦波電圧信号を生成するオペアンプベースの発振器は、 Wien bridge oscillator。
ザ・ circuit diagram ウィーンブリッジ発振器の概要を次の図に示します。
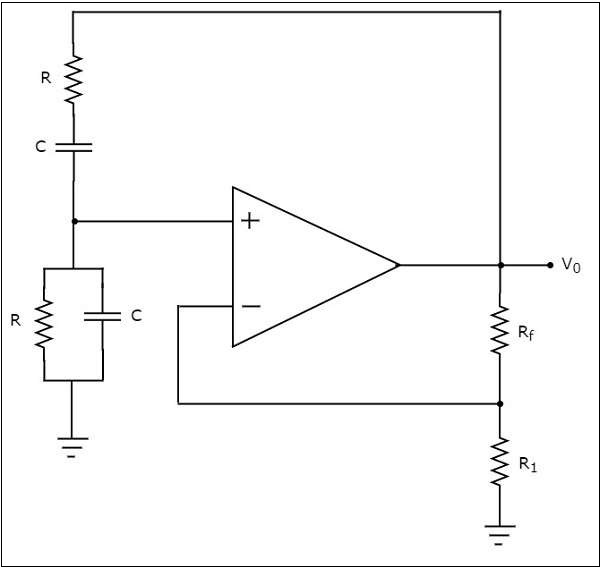
上記のウィーンブリッジ発振器の回路では、オペアンプは non inverting mode。したがって、00の位相シフトを提供します。したがって、上記の回路に存在するフィードバックネットワークは位相シフトを提供しないはずです。
フィードバックネットワークが何らかの位相シフトを提供する場合は、 balance the bridge位相シフトがあってはならないような方法で。だから、上記回路は、0の全位相シフト提供0いくつかの周波数です。
ザ・ output frequency ウィーンブリッジ発振器の
$$f=\frac{1}{2\Pi RC}$$
ザ・ gain $A_{v}$ 非反転増幅器のは3以上である必要があります
$$i.e.,1+\frac{R_f}{R_1}\geq3$$
$$=>\frac{R_f}{R_1}\geq2$$
$$=>R_{f}\geq2R_{1}$$
したがって、フィードバック抵抗の値を考慮する必要があります $R_{f}$ 抵抗器の値の少なくとも2倍、 $R_{1}$ ウィーンブリッジ発振器の出力で持続的な振動を生成するため。
A waveform generatorは、標準波を生成する電子回路です。オペアンプベースの波形発生器には2つのタイプがあります-
- 方形波発生器
- 三角波発生器
この章では、これらのオペアンプベースの波形ジェネレータのそれぞれについて詳しく説明します。
方形波発生器
A square wave generator方形波を発生させる電子回路です。このセクションでは、オペアンプベースの方形波発生器について説明します。
ザ・ circuit diagram オペアンプベースの方形波発生器の例を次の図に示します。
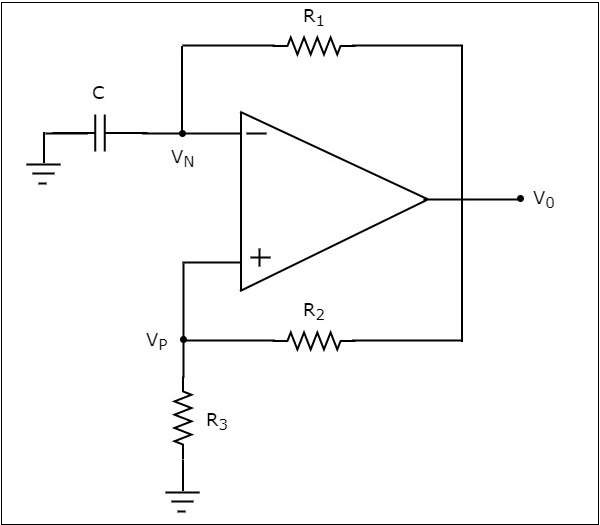
上記の回路図で、抵抗器が $R_{1}$オペアンプの反転入力端子とオペアンプの出力の間に接続されています。だから、抵抗器$R_{1}$ で使用されます negative feedback。同様に、抵抗器$R_{2}$オペアンプの非反転入力端子とその出力の間に接続されています。だから、抵抗器$R_{2}$ で使用されます positive feedback 道。
コンデンサCは、オペアンプの反転入力端子とグランドの間に接続されています。だから、voltage across capacitor Cオペアンプのこの反転端子の入力電圧になります。同様に、抵抗器$R_{3}$オペアンプの非反転入力端子とグランドの間に接続されています。だから、voltage across resistor $R_{3}$ オペアンプのこの非反転端子の入力電圧になります。
ザ・ operation 方形波発生器の概要は以下のとおりです。
あると仮定します no charge最初にコンデンサに保存されます。その場合、オペアンプの反転端子に存在する電圧はゼロボルトです。ただし、オペアンプの非反転端子にはオフセット電圧があります。このため、上記の回路の出力に存在する値は次のようになります。$+V_{sat}$。
さて、コンデンサCが始まります charging 抵抗器を介して $R_{1}$。上記の回路の出力に存在する値は次のように変化します。$-V_{sat}$、コンデンサCの両端の電圧が抵抗の両端の電圧(正の値)よりもわずかに大きくなったとき $R_{3}$。
コンデンサCが始動します discharging 抵抗器を介して $R_{1}$、上記回路の出力が $-V_{sat}$。上記の回路の出力に存在する値はに変化します$+V_{sat}$、コンデンサCの両端の電圧が抵抗の両端の電圧(負の値)よりもわずかに小さい(負の値)に達したとき $R_{3}$。
したがって、上の図に示されている回路は、 square wave 次の図に示すように出力で-

上の図から、方形波発生器の出力は次の2つの値のいずれかになることがわかります。 $+V_{sat}$ そして $-V_{sat}$。したがって、出力は一定期間1つの値に留まり、その後別の値に遷移して一定期間そこに留まります。このように、それは続きます。
三角波発生器
三角波発生器は、三角波を発生させる電子回路です。ザ・block diagram 三角波発生器の例を次の図に示します。

三角波発生器のブロック図には、主に方形波発生器と積分器の2つのブロックが含まれています。これらの2つのブロックはcascaded。つまり、方形波発生器の出力は積分器の入力として適用されます。方形波の積分は三角波に他ならないことに注意してください。
ザ・ circuit diagram オペアンプベースの三角波発生器の特性を次の図に示します。

方形波発生器と積分器の回路図はすでに見てきました。上記を取得したことを確認してくださいcircuit diagram 三角波発生器のブロック図のそれぞれの回路図でブロックを置き換えることによるオペアンプベースの三角波発生器の設計。
ザ・ 555 Timer ICは3つからその名前を得ました $5K\Omega$分圧器ネットワークで使用される抵抗器。このICは、正確な時間遅延と発振を生成するのに役立ちます。この章では、555タイマーについて詳しく説明します。
ピンダイアグラムと機能ダイアグラム
このセクションでは、最初に555タイマーICのピン配列について説明し、次にその機能図について説明します。
ピン配列
555タイマーICは、8ピンミニデュアルインラインパッケージ(DIP)です。ザ・pin diagram 555タイマーICの概要を次の図に示します。
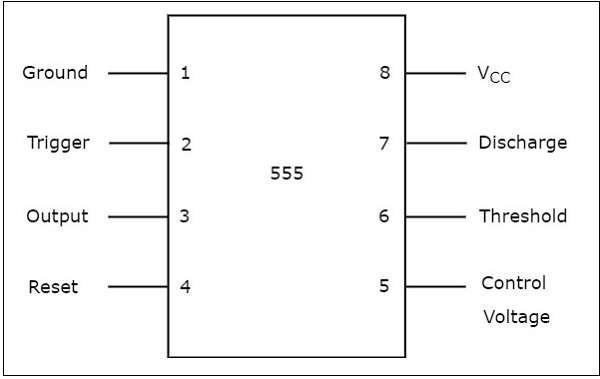
各ピンの重要性は、上の図から自明です。この555タイマーICは、+ 5V〜 + 18VのDC電源で動作します。主に生成に役立ちますnon-sinusoidal 正方形、ランプ、パルスなどの波形
機能図
555タイマーの内部の詳細を示す図解は、機能図として知られています。
ザ・ functional diagram 555タイマーICのは次の図に示されています-
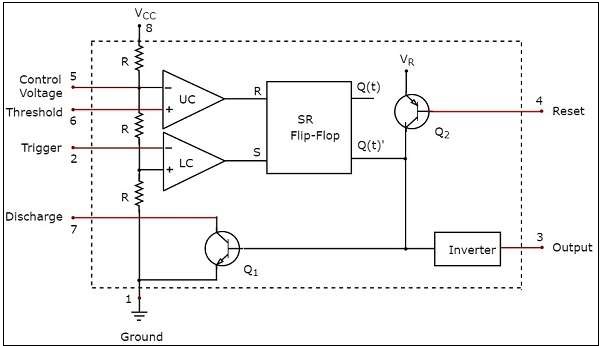
555タイマーの機能図には、分圧器ネットワーク、2つのコンパレータ、1つのSRフリップフロップ、2つのトランジスタ、およびインバータが含まれていることに注意してください。このセクションでは、各ブロックまたはコンポーネントの目的について詳しく説明します。
分圧器ネットワーク
分圧器ネットワークは3つで構成されています $5K\Omega$ 供給電圧間に直列に接続された抵抗器 $V_{cc}$ と地面。
このネットワークは、 $\frac{V_{cc} }{3}$ between a point and ground, if there exists only one $5K\Omega$ resistor. Similarly, it provides a voltage of $\frac{2V_{cc} }{3}$ between a point and ground, if there exists only two $5K\Omega$ resistors.
Comparator
The functional diagram of a 555 Timer IC consists of two comparators: an Upper Comparator (UC) and a Lower Comparator (LC).
Recall that a comparator compares the two inputs that are applied to it and produces an output.
If the voltage present at the non-inverting terminal of an op-amp is greater than the voltage present at its inverting terminal, then the output of comparator will be $+V_{sat}$. This can be considered as Logic High ('1') in digital representation.
If the voltage present at the non-inverting terminal of op-amp is less than or equal to the voltage at its inverting terminal, then the output of comparator will be $-V_{sat}$. This can be considered as Logic Low ('0') in digital representation.
SR Flip-Flop
Recall that a SR flip-flop operates with either positive clock transitions or negative clock transitions. It has two inputs: S and R, and two outputs: Q(t) and Q(t)’. The outputs, Q(t) & Q(t)’ are complement to each other.
The following table shows the state table of a SR flip-flop
| S | R | Q(t+1) |
|---|---|---|
| 0 | 0 | Q(t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | - |
Here, Q(t) & Q(t+1) are present state & next state respectively. So, SR flip-flop can be used for one of these three functions such as Hold, Reset & Set based on the input conditions, when positive (negative) transition of clock signal is applied.
The outputs of Lower Comparator (LC) and Upper Comparator (UC) are applied as inputs of SR flip-flop as shown in the functional diagram of 555 Timer IC.
Transistors and Inverter
The functional diagram of a 555 Timer IC consists of one npn transistor $Q_{1}$ and one pnp transistor $Q_{2}$. The npn transistor $Q_{1}$ will be turned ON if its base to emitter voltage is positive and greater than cut-in voltage. Otherwise, it will be turned-OFF.
The pnp transistor $Q_{2}$ is used as buffer in order to isolate the reset input from SR flip-flop and npn transistor $Q_{1}$.
The inverter used in the functional diagram of a 555 Timer IC not only performs the inverting action but also amplifies the power level.
The 555 Timer IC can be used in mono stable operation in order to produce a pulse at the output. Similarly, it can be used in astable operation in order to produce a square wave at the output.
Phase Locked Loop (PLL) is one of the vital blocks in linear systems. It is useful in communication systems such as radars, satellites, FMs, etc.
This chapter discusses about the block diagram of PLL and IC 565 in detail.
Block Diagram of PLL
A Phase Locked Loop (PLL) mainly consists of the following three blocks −
- Phase Detector
- Active Low Pass Filter
- Voltage Controlled Oscillator (VCO)
The block diagram of PLL is shown in the following figure −
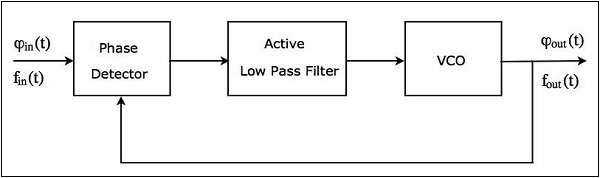
The output of a phase detector is applied as an input of active low pass filter. Similarly, the output of active low pass filter is applied as an input of VCO.
The working of a PLL is as follows −
Phase detector produces a DC voltage, which is proportional to the phase difference between the input signal having frequency of $f_{in}$ and feedback (output) signal having frequency of $f_{out}$.
A Phase detector is a multiplier and it produces two frequency components at its output − sum of the frequencies $f_{in}$ and $f_{out}$ and difference of frequencies $f_{in}$ & $f_{out}$.
An active low pass filter produces a DC voltage at its output, after eliminating high frequency component present in the output of the phase detector. It also amplifies the signal.
A VCO produces a signal having a certain frequency, when there is no input applied to it. This frequency can be shifted to either side by applying a DC voltage to it. Therefore, the frequency deviation is directly proportional to the DC voltage present at the output of a low pass filter.
The above operations take place until the VCO frequency equals to the input signal frequency. Based on the type of application, we can use either the output of active low pass filter or output of a VCO. PLLs are used in many applications such as FM demodulator, clock generator etc.
PLL operates in one of the following three modes −
- Free running mode
- Capture mode
- Lock mode
Initially, PLL operates in free running mode when no input is applied to it. When an input signal having some frequency is applied to PLL, then the output signal frequency of VCO will start change. At this stage, the PLL is said to be operating in the capture mode. The output signal frequency of VCO will change continuously until it is equal to the input signal frequency. Now, it is said to be PLL is operating in the lock mode.
IC 565
IC 565 is the most commonly used phase locked loop IC. It is a 14 pin Dual-Inline Package (DIP). The pin diagram of IC 565 is shown in the following figure −
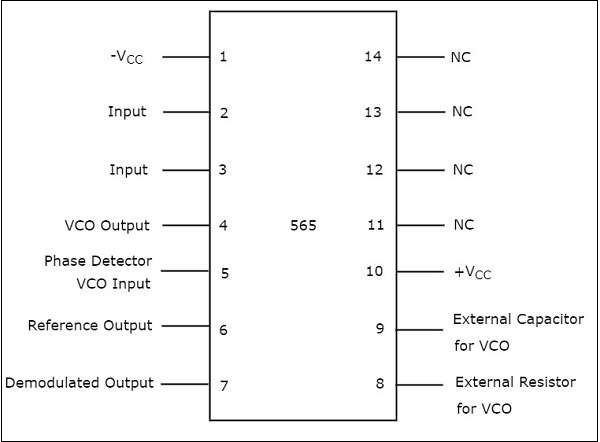
The purpose of each pin is self-explanatory from the above diagram. Out of 14 pins, only 10 pins (pin number 1 to 10) are utilized for the operation of PLL. So, the remaining 4 pins (pin number 11 to 14) are labelled with NC (No Connection).
The VCO produces an output at pin number 4 of IC 565, when the pin numbers 2 and 3 are grounded. Mathematically, we can write the output frequency, $f_{out}$ of the VCO as.
$$f_{out}=\frac{0.25}{R_VC_V}$$
where,
$R_{V}$ is the external resistor that is connected to the pin number 8
$C_{V}$ is the external capacitor that is connected to the pin number 9
By choosing proper values of $R_{V}$ and $C_{V}$, we can fix (determine) the output frequency, $f_{out}$ of VCO.
Pin numbers 4 and 5are to be shorted with an external wire so that the output of VCO can be applied as one of the inputs of phase detector.
IC 565 has an internal resistance of $3.6K\Omega$. A capacitor, C has to be connected between pin numbers 7 and 10 in order to make a low pass filter with that internal resistance.
Note that as per the requirement, we have to properly configure the pins of IC 565.
The function of a voltage regulator is to maintain a constant DC voltage at the output irrespective of voltage fluctuations at the input and (or) variations in the load current. In other words, voltage regulator produces a regulated DC output voltage.
Voltage regulators are also available in Integrated Circuits (IC) forms. These are called as voltage regulator ICs.
Types of Voltage Regulators
There are two types of voltage regulators −
- Fixed voltage regulator
- Adjustable voltage regulator
This chapter discusses about these two types of voltage regulators one by one.
Fixed voltage regulator
A fixed voltage regulator produces a fixed DC output voltage, which is either positive or negative. In other words, some fixed voltage regulators produce positive fixed DC voltage values, while others produce negative fixed DC voltage values.
78xx voltage regulator ICs produce positive fixed DC voltage values, whereas, 79xx voltage regulator ICs produce negative fixed DC voltage values.
The following points are to be noted while working with 78xx and 79xx voltage regulator ICs −
“xx” corresponds to a two-digit number and represents the amount (magnitude) of voltage that voltage regulator IC produces.
Both 78xx and 79xx voltage regulator ICs have 3 pins each and the third pin is used for collecting the output from them.
The purpose of the first and second pins of these two types of ICs is different −
The first and second pins of 78xx voltage regulator ICs are used for connecting the input and ground respectively.
The first and second pins of 79xx voltage regulator ICs are used for connecting the ground and input respectively.
Examples
- 7805 voltage regulator IC produces a DC voltage of +5 volts.
- 7905 voltage regulator IC produces a DC voltage of -5 volts.
The following figure shows how to produce a fixed positive voltage at the output by using a fixed positive voltage regulator with necessary connections.
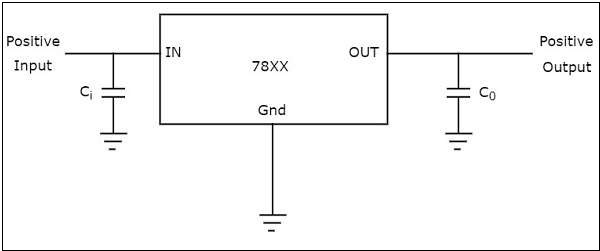
In the above figure that shows a fixed positive voltage regulator, the input capacitor Ci is used to prevent unwanted oscillations and the output capacitor, C0 acts as a line filter to improve transient response.
Note − an get a fixed negative voltage at the output by using a fixed negative voltage regulator with suitable connections.
Adjustable voltage regulator
An adjustable voltage regulator produces a DC output voltage, which can be adjusted to any other value of certain voltage range. Hence, adjustable voltage regulator is also called as a variable voltage regulator.
The DC output voltage value of an adjustable voltage regulator can be either positive or negative.
LM317 voltage regulator IC
LM317 voltage regulator IC can be used for producing a desired positive fixed DC voltage value of the available voltage range.
LM317 voltage regulator IC has 3 pins. The first pin is used for adjusting the output voltage, second pin is used for collecting the output and third pin is used for connecting the input.
The adjustable pin (terminal) is provided with a variable resistor which lets the output to vary between a wide range.

The above figure shows an unregulated power supply driving a LM 317 voltage regulator IC, which is commonly used. This IC can supply a load current of 1.5A over an adjustable output range of 1.25 V to 37 V.
All the real world quantities are analog in nature. We can represent these quantities electrically as analog signals. An analog signal is a time varying signal that has any number of values (variations) for a given time slot.
In contrast to this, a digital signal varies suddenly from one level to another level and will have only finite number of values (variations) for a given time slot.
This chapter discusses about the types of data converters and their specifications.
Types of Data Converters
The electronic circuits, which can be operated with analog signals are called as analog circuits. Similarly, the electronic circuits, which can be operated with digital signals are called as digital circuits. A data converter is an electronic circuit that converts data of one form to another.
There are two types of data converters −
- Analog to Digital Converter
- Digital to Analog Converter
If we want to connect the output of an analog circuit as an input of a digital circuit, then we have to place an interfacing circuit between them. This interfacing circuit that converts the analog signal into digital signal is called as Analog to Digital Converter.
Similarly, if we want to connect the output of a digital circuit as an input of an analog circuit, then we have to place an interfacing circuit between them. This interfacing circuit that converts the digital signal into an analog signal is called as Digital to Analog Converter.
Note that some Analog to Digital Converters may require Digital to Analog Converter as an internal block for their operation.
Specifications
The following are the specifications that are related to data conversions −
- Resolution
- Conversion Time
Resolution
Resolution is the minimum amount of change needed in an analog input voltage for it to be represented in binary (digital) output. It depends on the number of bits that are used in the digital output.
Mathematically, resolution can be represented as
$$Resolution=\frac{1}{2^{N}}$$
where, ‘N’ is the number of bits that are present in the digital output.
From the above formula, we can observe that there exists an inverse relationship between the resolution and number of bits. Therefore, resolution decreases as the number of bits increases and vice-versa.
Resolution can also be defined as the ratio of maximum analog input voltage that can be represented in binary and the equivalent binary number.
Mathematically, resolution can be represented as
$$Resolution=\frac{V_{FS}}{2^{N}-1}$$
where,
$V_{FS}$ is the full scale input voltage or maximum analog input voltage,
‘N’ is the number of bits that are present in the digital output.
Conversion Time
The amount of time required for a data converter in order to convert the data (information) of one form into its equivalent data in other form is called as conversion time. Since we have two types of data converters, there are two types of conversion times as follows
- Analog to Digital Conversion time
- Digital to Analog Conversion time
The amount of time required for an Analog to Digital Converter (ADC) to convert the analog input voltage into its equivalent binary (digital) output is called as Analog to Digital conversion time. It depends on the number of bits that are used in the digital output.
The amount of time required for a Digital to Analog Converter (DAC) to convert the binary (digital) input into its equivalent analog output voltage is called as Digital to Analog conversion time. It depends on the number of bits that are present in the binary (digital) input.
A Digital to Analog Converter (DAC) converts a digital input signal into an analog output signal. The digital signal is represented with a binary code, which is a combination of bits 0 and 1. This chapter deals with Digital to Analog Converters in detail.
The block diagram of DAC is shown in the following figure −
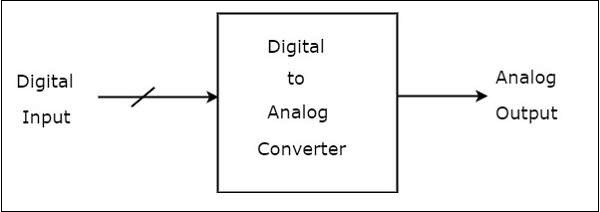
A Digital to Analog Converter (DAC) consists of a number of binary inputs and a single output. In general, the number of binary inputs of a DAC will be a power of two.
Types of DACs
There are two types of DACs
- Weighted Resistor DAC
- R-2R Ladder DAC
This section discusses about these two types of DACs in detail −
Weighted Resistor DAC
A weighted resistor DAC produces an analog output, which is almost equal to the digital (binary) input by using binary weighted resistors in the inverting adder circuit. In short, a binary weighted resistor DAC is called as weighted resistor DAC.
The circuit diagram of a 3-bit binary weighted resistor DAC is shown in the following figure −

Recall that the bits of a binary number can have only one of the two values. i.e., either 0 or 1. Let the 3-bit binary input is $b_{2}b_{1}b_{0}$. Here, the bits $b_{2}$ and $b_{0}$ denote the Most Significant Bit (MSB) and Least Significant Bit (LSB) respectively.
The digital switches shown in the above figure will be connected to ground, when the corresponding input bits are equal to ‘0’. Similarly, the digital switches shown in the above figure will be connected to the negative reference voltage, $-V_{R}$ when the corresponding input bits are equal to ‘1’.
In the above circuit, the non-inverting input terminal of an op-amp is connected to ground. That means zero volts is applied at the non-inverting input terminal of op-amp.
According to the virtual short concept, the voltage at the inverting input terminal of opamp is same as that of the voltage present at its non-inverting input terminal. So, the voltage at the inverting input terminal’s node will be zero volts.
The nodal equation at the inverting input terminal’s node is:
$$\frac{0+V_{R}b_{2}}{2^{0}R}+\frac{0+V_{R}b_{1}}{2^{1}R}+\frac{0+V_{R}b_{0}}{2^{2}R}+\frac{0-V_{0}}{R_{f}}=0$$
$$=>\frac{V_{0}}{R_{f}}=\frac{V_{R}b_{2}}{2^{0}R}+\frac{V_{R}b_{1}}{2^{1}R}+\frac{V_{R}b_{0}}{2^{2}R}$$
$$=>V_{0}=\frac{V_{R}R_{f}}{R}\left \{\frac{b_{2}}{2^{0}}+\frac{b_{1}}{2^{1}}+\frac{b_{0}}{2^{2}}\right \}$$
Substituting, $R=2R_{f}$ in above equation.
$$=>V_{0}=\frac{V_{R}R_{f}}{2R_{f}}\left \{\frac{b_{2}}{2^{0}}+\frac{b_{1}}{2^{1}}+\frac{b_{0}}{2^{2}}\right \}$$
$$=>V_{0}=\frac{V_{R}}{2}\left \{\frac{b_{2}}{2^{0}}+\frac{b_{1}}{2^{1}}+\frac{b_{0}}{2^{2}}\right \}$$
The above equation represents the output voltage equation of a 3-bit binary weighted resistor DAC. Since the number of bits are three in the binary (digital) input, we will get seven possible values of output voltage by varying the binary input from 000 to 111 for a fixed reference voltage, $V_{R}$.
We can write the generalized output voltage equation of an N-bit binary weighted resistor DAC as shown below based on the output voltage equation of a 3-bit binary weighted resistor DAC.
$$=>V_{0}=\frac{V_{R}}{2}\left \{ \frac{b_{N-1}}{2^{0}}+ \frac{b_{N-2}}{2^{1}}+....+\frac{b_{0}}{2^{N-1}} \right \}$$
The disadvantages of a binary weighted resistor DAC are as follows −
The difference between the resistance values corresponding to LSB & MSB will increase as the number of bits present in the digital input increases.
It is difficult to design more accurate resistors as the number of bits present in the digital input increases.
R-2R Ladder DAC
The R-2R Ladder DAC overcomes the disadvantages of a binary weighted resistor DAC. As the name suggests, R-2R Ladder DAC produces an analog output, which is almost equal to the digital (binary) input by using a R-2R ladder network in the inverting adder circuit.
Thecircuit diagramof a 3-bit R-2R Ladder DAC is shown in the following figure −
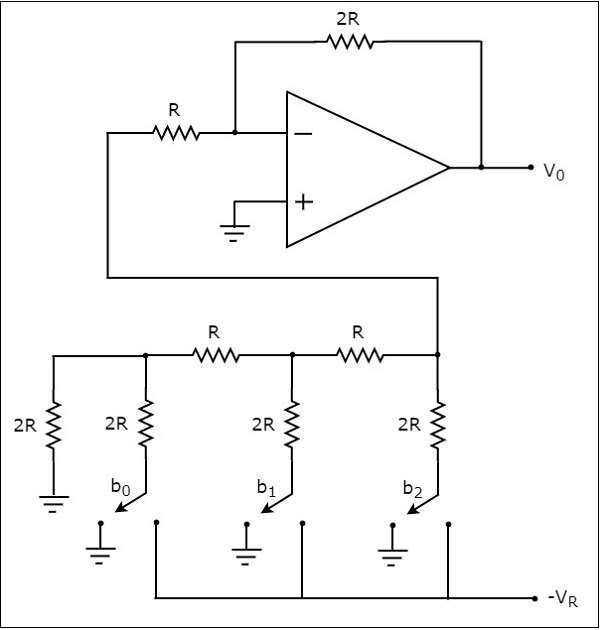
Recall that the bits of a binary number can have only one of the two values. i.e., either 0 or 1. Let the 3-bit binary input is $b_{2}b_{1}b_{0}$. Here, the bits $b_{2}$ and $b_{0}$ denote the Most Significant Bit (MSB) and Least Significant Bit (LSB) respectively.
The digital switches shown in the above figure will be connected to ground, when the corresponding input bits are equal to ‘0’. Similarly, the digital switches shown in above figure will be connected to the negative reference voltage, $-V_{R}$ when the corresponding input bits are equal to ‘1’.
It is difficult to get the generalized output voltage equation of a R-2R Ladder DAC. But, we can find the analog output voltage values of R-2R Ladder DAC for individual binary input combinations easily.
The advantages of a R-2R Ladder DAC are as follows −
R-2R Ladder DAC contains only two values of resistor: R and 2R. So, it is easy to select and design more accurate resistors.
If more number of bits are present in the digital input, then we have to include required number of R-2R sections additionally.
上記の利点により、R-2RラダーDACはバイナリ加重抵抗DACよりも好ましいです。
前の章では、2種類のDACについて説明しました。この章では、R-2RラダーDACに基づく問題の例について説明します。
例
バイナリ入力のR-2RラダーDACのアナログ出力電圧の値を見つけましょう。 $b_{2}b_{1}b_{0}$ = 100。
回路図とその簡略化
ザ・ circuit diagram バイナリ入力時の3ビットR-2RラダーDACの場合、 $b_{2}b_{1}b_{0}$ = 100を適用すると次の図に示されます-
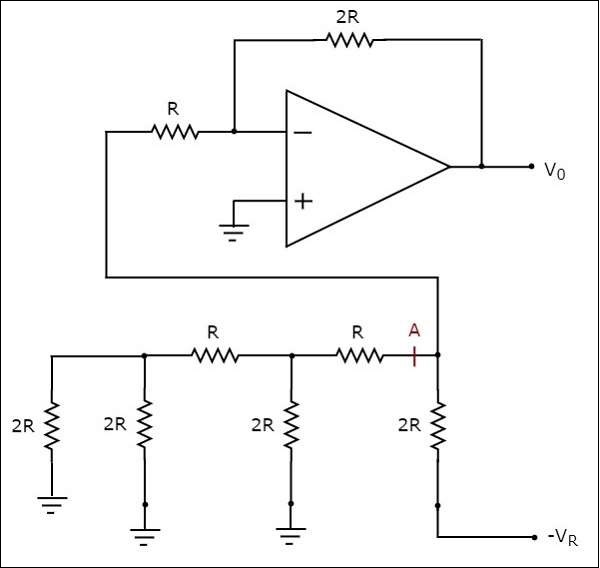
上記の回路では、左側に抵抗の直列および並列の組み合わせが存在します point A地面に関して。したがって、その抵抗ネットワーク全体を、次の抵抗を持つ単一の抵抗に置き換えることができます。$2R\Omega$。
ザ・ simplified circuit diagram 次の図に示します-
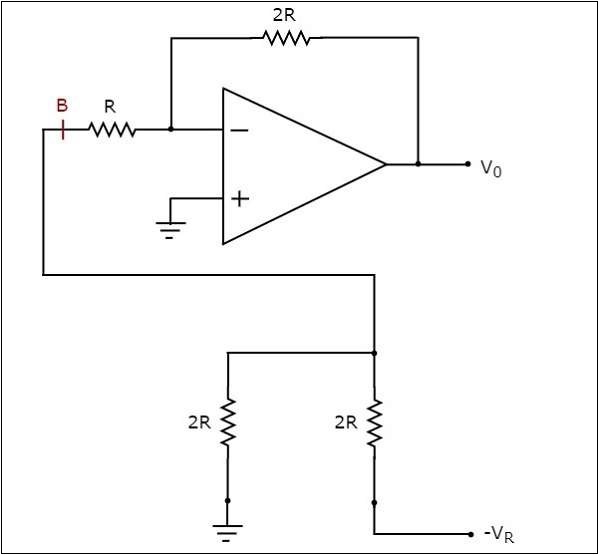
テブナンの等価回路を使用して、アースに対してポイントBの左側に接続されているネットワークの部分を置き換えることができます。ザ・modified circuit diagram 次の図に示します-

上記の回路には、2つの抵抗の直列の組み合わせが存在します。この組み合わせを単一の抵抗器に置き換えます。最終circuit diagram 簡略化した後を次の図に示します-
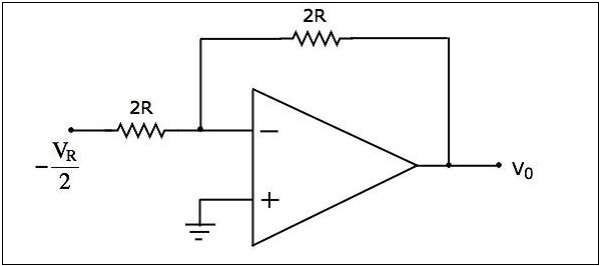
さて、上の回路図は次のようになります inverting amplifier。入力電圧は$-\frac{V_{R}}{2}$ ボルト、入力抵抗 $2R\Omega$ とフィードバック抵抗 $2R\Omega$。
ザ・ output voltage 上に示した回路の
$$V_{0}=-\frac{2R}{2R}\left(-\frac{V_{R}}{2}\right)$$
$$V_{0}=\frac{V_{R}}{2}$$
したがって、 output voltage 3ビットR-2RラダーDACの $\frac{V_{R}}{2}$ バイナリ入力のボルト、 $b_{2}b_{1}b_{0}$ = 100。
アナログ-デジタルコンバーター (ADC)アナログ信号をデジタル信号に変換します。デジタル信号は、ビット0と1の組み合わせであるバイナリコードで表されます。
ザ・ block diagram ADCの特性を次の図に示します-
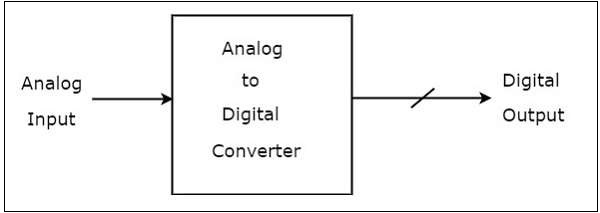
上に示した図では、アナログ-デジタルコンバーターに注意してください。 (ADC)単一のアナログ入力と多くのバイナリ出力で構成されます。一般に、ADCのバイナリ出力の数は2の累乗になります。
がある two typesADCの種類:直接型ADCと間接型ADC。この章では、ダイレクトタイプADCについて詳しく説明します。
ADCが内部で生成された同等のデジタル(バイナリ)コードを利用してアナログ入力と比較することにより、アナログからデジタルへの変換を直接実行する場合、それは次のように呼ばれます。 Direct type ADC。
以下は examples ダイレクトタイプADCの
- カウンタ型ADC
- 逐次比較ADC
- フラッシュ型ADC
このセクションでは、これらのダイレクトタイプADCについて詳しく説明します。
カウンタ型ADC
A counter type ADC 内部でカウンタ演算を使用することにより、アナログ入力とほぼ等しいデジタル出力を生成します。
ザ・ block diagram カウンタ型ADCの例を次の図に示します。
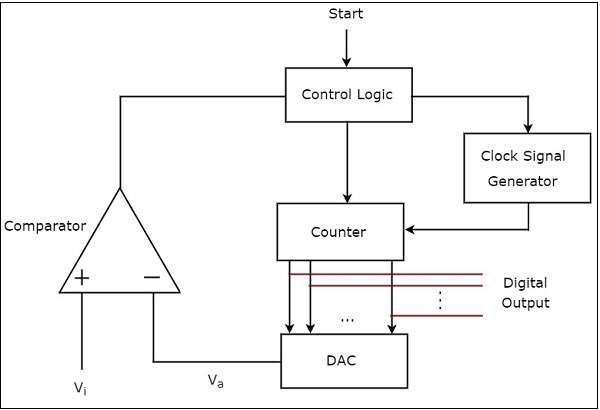
カウンタタイプのADCは、主にクロック信号ジェネレータ、カウンタ、DAC、コンパレータ、制御ロジックの5つのブロックで構成されています。
ザ・ working カウンタ型ADCの例は次のとおりです。
ザ・ control logic カウンタをリセットし、クロック信号ジェネレータを有効にして、開始コマンド信号を受信したときにクロックパルスをカウンタに送信します。
ザ・ counterクロックパルスごとに1ずつインクリメントされ、その値はバイナリ(デジタル)形式になります。このカウンタの出力は、DACの入力として適用されます。
DACカウンタの出力である受信したバイナリ(デジタル)入力をアナログ出力に変換します。コンパレータはこのアナログ値を比較し、$V_{a}$ 外部アナログ入力値で $V_{i}$。
ザ・ output of comparator になります ‘1’より大きい限り。上記の2つのステップで説明した操作は、制御ロジックがコンパレータの出力から「1」を受信する限り継続されます。
ザ・ output of comparator になります ‘0’ いつ $V_{i}$ 以下である $V_{a}$。したがって、制御ロジックはコンパレータの出力から「0」を受け取ります。次に、制御ロジックはクロック信号ジェネレータを無効にして、カウンタにクロックパルスを送信しないようにします。
この時点で、カウンターの出力は次のように表示されます。 digital output。対応する外部アナログ入力値とほぼ同等です$V_{i}$。
逐次比較ADC
A successive approximation type ADC 内部で逐次比較手法を使用することにより、アナログ入力とほぼ等しいデジタル出力を生成します。
ザ・ block diagram 逐次比較ADCの例を次の図に示します。

逐次比較ADCは、主に5つのブロック(クロック信号ジェネレータ、逐次比較レジスタ(SAR)、DAC、コンパレータ、および制御ロジック)で構成されています。
ザ・ working 逐次比較ADCの特性は次のとおりです。
ザ・ control logic SARのすべてのビットをリセットし、クロック信号発生器が開始コマンド信号を受信すると、クロックパルスをSARに送信できるようにします。
に存在するバイナリ(デジタル)データ SARコンパレータの出力に基づいて、クロックパルスごとに更新されます。SARの出力はDACの入力として適用されます。
DAC SARの出力である受信デジタル入力をアナログ出力に変換します。コンパレータはこのアナログ値を比較します$V_{a}$ 外部アナログ入力値で $V_{i}$。
ザ・ output of a comparator 限り「1」になります $V_{i}$ より大きい $V_{a}$。同様に、コンパレータの出力は「0」になります。$V_{i}$ 以下である $V_{a}$。
上記の手順は、デジタル出力が有効になるまで続行されます。
デジタル出力は、対応する外部アナログ入力値とほぼ同等である場合、有効な出力になります。 $V_{i}$。
フラッシュ型ADC
A flash type ADC対応するアナログ入力と同等のデジタル出力をすぐに生成します。したがって、フラッシュタイプADCは最速のADCです。
ザ・ circuit diagram 3ビットフラッシュタイプADCの例を次の図に示します。
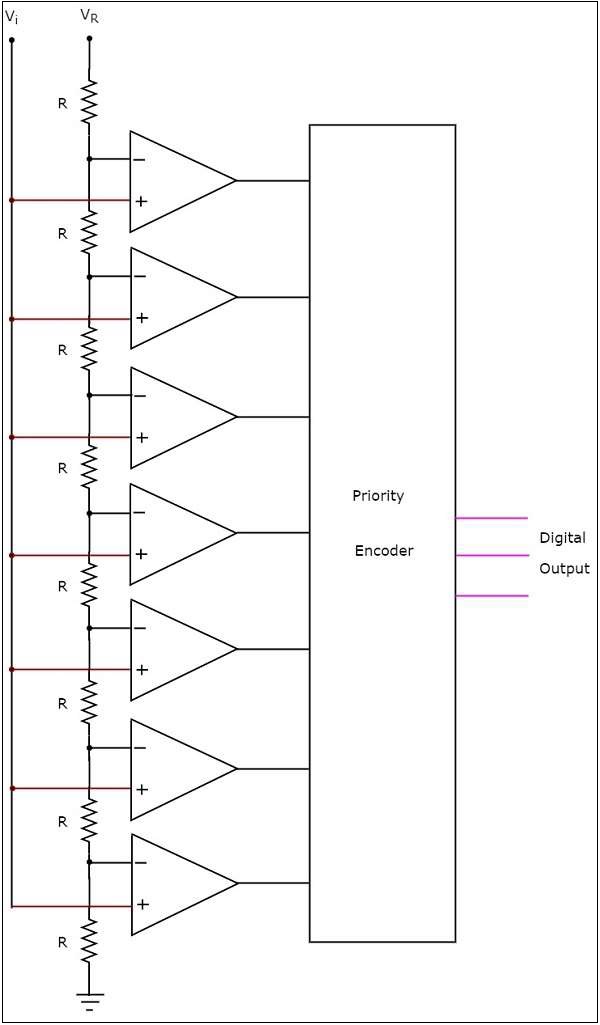
3ビットフラッシュタイプADCは、分圧器ネットワーク、7つのコンパレータ、およびプライオリティエンコーダで構成されています。
ザ・ working 3ビットフラッシュタイプADCの特性は次のとおりです。
ザ・ voltage divider network8つの等しい抵抗が含まれています。基準電圧$V_{R}$地面に関してそのネットワーク全体に適用されます。グランドに対して下から上への各抵抗器の両端の電圧降下は、の整数倍(1から8)になります。$\frac{V_{R}}{8}$。
外部 input voltage $V_{i}$すべてのコンパレータの非反転端子に適用されます。各抵抗器のグランドに対する下から上への電圧降下は、コンパレータの反転端子に下から上に適用されます。
一度に、すべてのコンパレータが外部入力電圧をそれぞれの他の入力端子に存在する電圧降下と比較します。つまり、比較操作は各コンパレータによって行われます。parallelly。
ザ・ output of the comparator 限り「1」になります $V_{i}$それぞれの他の入力端子に存在する電圧降下よりも大きい。同様に、コンパレータの出力は「0」になります。$V_{i}$ は、他のそれぞれの入力端子に存在する電圧降下以下です。
コンパレータのすべての出力は、の入力として接続されています。 priority encoderこのプライオリティエンコーダは、「1」を持つ高プライオリティ入力に対応するバイナリコード(デジタル出力)を生成します。
したがって、プライオリティエンコーダの出力はバイナリに相当します (digital output) 外部アナログ入力電圧の $V_{i}$。
フラッシュタイプADCは、アナログ入力からデジタルデータへの変換速度が非常に速いアプリケーションで使用されます。
前の章では、ADCとは何か、およびダイレクトタイプADCの例について説明しました。この章では、間接型ADCについて説明します。
ADCが間接的な方法でアナログからデジタルへの変換を実行する場合、それは Indirect type ADC。一般に、最初にアナログ入力を時間(または周波数)の線形関数に変換し、次にデジタル(バイナリ)出力を生成します。
デュアルスロープADCは最高です example間接型ADCの。この章では、それについて詳しく説明します。
デュアルスロープADC
名前が示すように、 dual slope ADC 2つの(デュアル)スロープ技術を使用して、対応するアナログ入力と同等のデジタル出力を生成します。
ザ・ block diagram デュアルスロープADCの特性を次の図に示します-
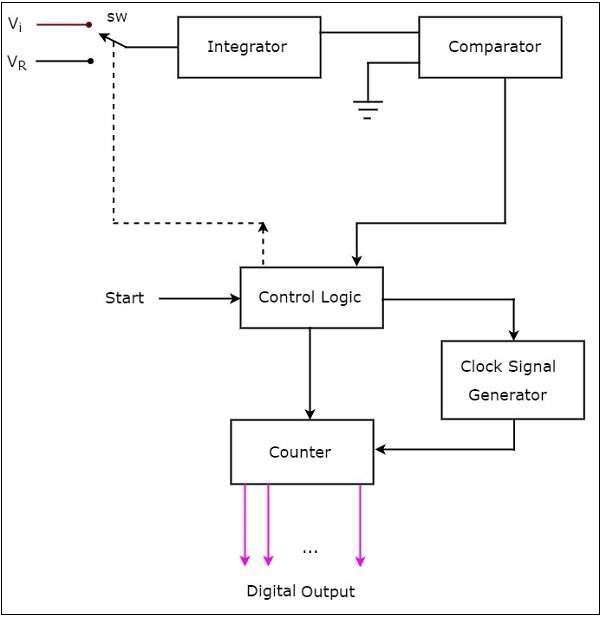
デュアルスロープADCは、主に5つのブロックで構成されています。積分器、コンパレータ、クロック信号ジェネレータ、制御ロジック、およびカウンタです。
ザ・ working デュアルスロープADCの特性は次のとおりです-
ザ・ control logic 開始指令信号を受信すると、カウンタをリセットし、クロック信号ジェネレータを有効にして、クロックパルスをカウンタに送信します。
制御ロジックがスイッチを押す sw に接続するには external analog input voltage $V_{i}$、開始コマンド信号を受信すると。この入力電圧は積分器に印加されます。
の出力 integrator はコンパレータの2つの入力の1つに接続され、コンパレータのもう1つの入力はグランドに接続されます。
Comparator 積分器の出力をゼロボルト(グランド)と比較し、出力を生成します。これは制御ロジックに適用されます。
ザ・ counterクロックパルスごとに1ずつインクリメントされ、その値はバイナリ(デジタル)形式になります。最大カウント値に達した後にインクリメントされると、制御ロジックへのオーバーフロー信号を生成します。この時点で、カウンターのすべてのビットはゼロのみになります。
これで、制御ロジックがスイッチを押します sw に接続するには negative reference 電圧 $-V_{ref}$。この負の基準電圧は積分器に印加されます。コンデンサに蓄積された電荷をゼロになるまで取り除きます。
この時点で、コンパレータの両方の入力はゼロボルトになっています。そのため、コンパレータは制御ロジックに信号を送信します。ここで、制御ロジックはクロック信号発生器を無効にし、カウンタ値を保持(保持)します。ザ・counter value は外部アナログ入力電圧に比例します。
この時点で、カウンターの出力は次のように表示されます。 digital output。対応する外部アナログ入力値とほぼ同等です$V_{i}$。
デュアルスロープADCは、アプリケーションで使用されます。 accuracy アナログ入力を同等のデジタル(バイナリ)データに変換する際には、より重要です。