正弦波発振器

発振器は、周期的な信号を生成する電子回路です。発振器が正弦波振動を生成する場合、それはと呼ばれますsinusoidal oscillator。DC電源からの入力エネルギーを周期信号のAC出力エネルギーに変換します。この周期的な信号は、特定の周波数と振幅を持ちます。

ザ・ block diagram 正弦波発振器の特性を次の図に示します-

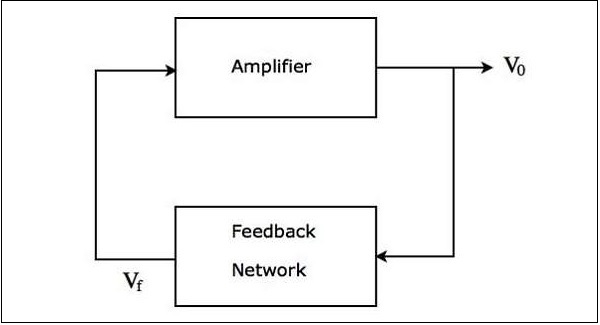
上の図は主に two blocks：増幅器とフィードバックネットワーク。フィードバックネットワークは、増幅器への入力として増幅器の出力の一部を取り、電圧信号を生成します。この電圧信号は、アンプへの入力として適用されます。

上に示した正弦波発振器のブロック図は、次の場合に正弦波振動を生成します。 two conditions 満足している−

ザ・ loop gain 上記の正弦波発振器のブロック図の$ A_ {v} \ beta $は、以上である必要があります。 unity。ここで、$ A_ {v} $と$ \ beta $は、それぞれ増幅器のゲインとフィードバックネットワークのゲインです。
合計 phase shift 正弦波発振器の上記のブロック図のループの周りは、次のいずれかである必要があります。 0⁰ または 360⁰。

上記の2つの条件を合わせて次のように呼びます。 Barkhausen criteria。

オペアンプベースのオシレータ

がある two オペアンプベースのオシレータのタイプ。

このセクションでは、それぞれについて詳しく説明します。

反転増幅器とフィードバックネットワークの助けを借りて出力に正弦波電圧信号を生成するオペアンプベースの発振器は、 RC phase shift oscillator。このフィードバックネットワークは、3つのカスケードされたRCセクションで構成されています。

ザ・ circuit diagram RC位相シフト発振器の概要を次の図に示します。

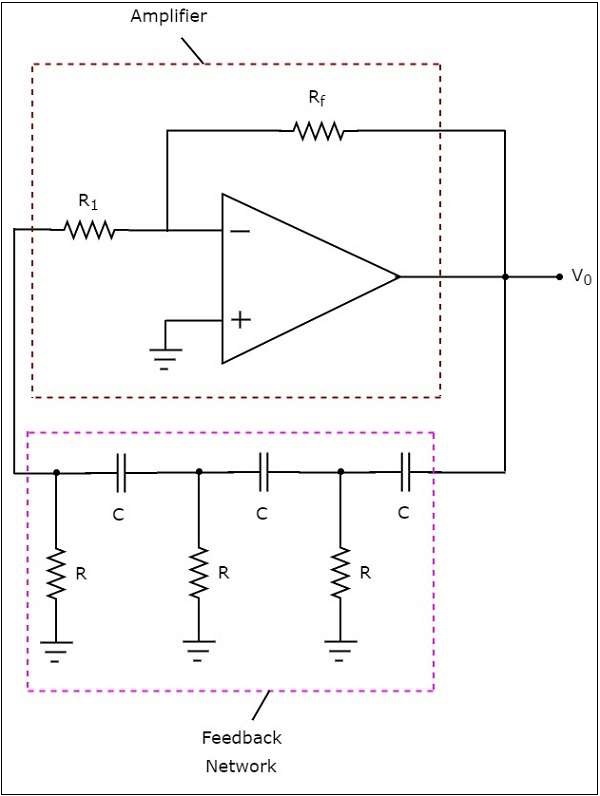
上記の回路では、オペアンプは inverting mode。したがって、180の位相シフトを提供⁰。上記回路の帰還ネットワークの存在はまた、180の位相シフトを提供^0を各RC部60の位相シフトを提供するので、⁰。従って、上記回路360の全位相シフト提供⁰いくつかの周波数です。

$$ f = \ frac {1} {2 \ Pi RC \ sqrt [] {6}} $$

$$ ie、-\ frac {R_f} {R_1} \ geq-29 $$

$$ => \ frac {R_f} {R_1} \ geq-29 $$

$$ => R_ {f} \ geq29R_ {1} $$

したがって、RC位相シフト発振器の出力で持続的な発振を生成するには、フィードバック抵抗$ R_ {f} $の値を抵抗$ R_ {1} $の値の29倍以上と見なす必要があります。

非反転増幅器とフィードバックネットワークの助けを借りて出力に正弦波電圧信号を生成するオペアンプベースの発振器は、 Wien bridge oscillator。

ザ・ circuit diagram ウィーンブリッジ発振器の概要を次の図に示します。

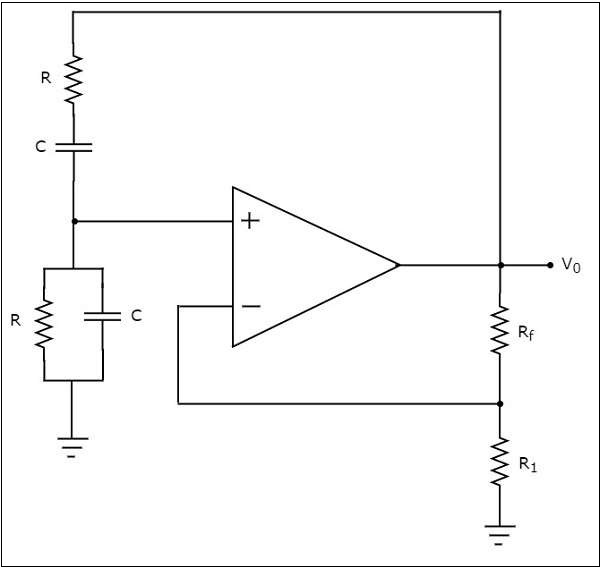
上記のウィーンブリッジ発振器の回路では、オペアンプは non inverting mode。したがって、00の位相シフトを提供します。したがって、上記の回路に存在するフィードバックネットワークは位相シフトを提供しないはずです。

フィードバックネットワークが何らかの位相シフトを提供する場合は、 balance the bridge位相シフトがないように。だから、上記回路は、0の全位相シフト提供⁰いくつかの周波数です。

$$ f = \ frac {1} {2 \ Pi RC} $$

$$ ie、1 + \ frac {R_f} {R_1} \ geq3 $$

$$ => \ frac {R_f} {R_1} \ geq2 $$

$$ => R_ {f} \ geq2R_ {1} $$

したがって、ウィーンブリッジ発振器の出力で持続的な発振を生成するには、フィードバック抵抗$ R_ {f} $の値を抵抗の値$ R_ {1} $の少なくとも2倍にする必要があります。