素因数分解

定義

Factors 別の数を得るために乗算する数です。

にとって example、2×7 = 14であるため、14の因数は2と7です。

一部の数値は、複数の方法で因数分解できます。

にとって example、16は、1×16、2×8、または4×4として因数分解できます。

それ自体が1回しか因数分解できない数は、 prime number。

最初のいくつかの素数は2、3、5、7、11、および13です。

複数の要素を持つ数はと呼ばれます composite numbers。

数1は素数でも合成数でもありません。

2つの要素の積として任意の整数を記述し、 factor tree。素因数は、さらに分解できない素因数のみが残るまで、さらに分解されます。

ほとんどの場合、を見つける必要があります prime factors 数の：与えられた数のすべての素数因子のリスト。

数をその素因数に因数分解し、その素因数の積として数を表現することは、 prime factorization その数の。

ザ・ prime factorization 数の数には素因数のみが含まれ、それらの素因数の積は含まれません。

Example

24の素因数を見つける

解決

Step 1:

24の素因数を見つけるには、それを均等に分割する最小の素数で除算します：24÷2 = 12。

Step 2:

ここで、12を均等に分割する最小の素数で除算します：12÷2 = 6。

Step 3:

ここで、6を均等に分割する最小の素数で除算します：6÷2 = 3。

Step 4:

3が素因数なので、因数分解が完了し、24の素因数分解は2×2×2×3になります。

問題1：

48のすべての素因数を見つけます。

解決

Step 1:

以下に示すように、48をその要因に分解することができます。

48 = 3×16;

16 = 2×8;

8 = 2×4;

4 = 2×2。

Step 2:

ここで得られる因子ツリーを以下に示します。

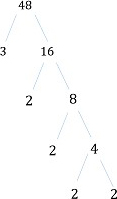
Step 3:

したがって、48の素因数分解または48の素因数分解の積として書かれた48は

48 = 2×2×2×2×3

問題2：

75のすべての素因数を見つけます。

解決

Step 1:

以下に示すように、75をその要因に分解できます。

75 = 3×25;

25 = 5×5;

Step 2:

ここで得られる因子ツリーを以下に示します。

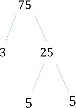
Step 3:

したがって、75は、その素因数または75の素因数分解の積として記述されます。

75 = 3×5×5