数直線上で線形不等式をグラフ化する
このレッスンでは、数直線を使用して不等式を表します。
以下の例では、与えられた不等式の真の値の範囲を示しています。
私たちは使用します open dot<および>関係を表すため。この記号は、数直線上の点が不等式の可能な値の範囲内に含まれていないことを示します。
私たちは使用します closed dot 不等式の両側が等しくなる可能性がある場合に、≤および≥を表す。
Number Line
数直線は、数に対応する点を持つ水平線であることを思い出してください。ポイントは、対応する番号の値に従って間隔が空けられます。ポイントは、整数または整数のみを含む数直線内で等間隔に配置されます。
Graph of the point “3”
数直線上の点として表すことにより、数値をグラフ化します。たとえば、以下に示すように、数直線上に「3」をグラフ化します。

Graph of the Inequality x ≤ 3
数直線上に不等式をグラフ化することもできます。次のグラフは、不等式x≤3を表しています。暗い線は、x≤3を満たすすべての数値を表しています。暗い線で任意の数値を選択し、それをxに接続すると、不等式は真になります。
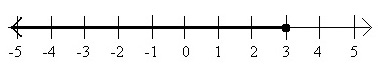
Graph of the Inequality x < 3
次のグラフは、不等式x <3を表しています。3の白丸は、3がx <3の解ではないことを示していることに注意してください。

Graph of the Inequality x > 3
これがそれぞれx> 3とx≥3のグラフです
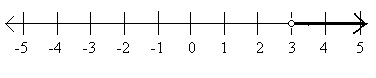
Graph of the Inequality x ≥ 3
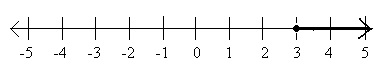
Graph of the Inequality x ≠ 3
「≠」記号の付いた不等式には、1つの点を除くすべての実数である解集合があります。したがって、「≠」記号の付いた不等式をグラフ化するには、1つの点を削除して線全体をグラフ化します。たとえば、グラフx≠3のは次のようになります-

次の不等式を数直線上にグラフ化します-
$\frac{x}{3}$ ≤ 7
解決
Step 1:
$\frac{x}{3}$≤7; x≤(7×3); x≤21
まず、数直線上の点21を見つけます。
Step 2:
21に閉じた円を置き、左に向かって太い線を引いて、不等式x≤21を示します。

次の不等式を数直線上にグラフ化します-
x > −32
解決
Step 1:
まず、数直線上の点-32を見つけます。
Step 2:
-32に白丸を置き、右に向かって太い線を引いて不等式を示します。
x> −32
