DAA-병합 정렬

이 장에서는 병합 정렬에 대해 논의하고 복잡성을 분석합니다.

문제 설명

숫자 목록을 정렬하는 문제는 즉시 분할 및 정복 전략에 적합합니다. 목록을 두 개로 분할하고 각 절반을 반복적으로 정렬 한 다음 두 개의 정렬 된 하위 목록을 병합합니다.

해결책

이 알고리즘에서 숫자는 배열에 저장됩니다. numbers[]. 여기,p 과 q 하위 배열의 시작 및 끝 인덱스를 나타냅니다.

Algorithm: Merge-Sort (numbers[], p, r) 
if p < r then  
q = ⌊(p + r) / 2⌋ 
Merge-Sort (numbers[], p, q) 
    Merge-Sort (numbers[], q + 1, r) 
    Merge (numbers[], p, q, r)

Function: Merge (numbers[], p, q, r)
n1 = q – p + 1 
n2 = r – q 
declare leftnums[1…n1 + 1] and rightnums[1…n2 + 1] temporary arrays 
for i = 1 to n1 
   leftnums[i] = numbers[p + i - 1] 
for j = 1 to n2 
   rightnums[j] = numbers[q+ j] 
leftnums[n1 + 1] = ∞ 
rightnums[n2 + 1] = ∞ 
i = 1 
j = 1 
for k = p to r 
   if leftnums[i] ≤ rightnums[j] 
      numbers[k] = leftnums[i] 
      i = i + 1 
   else
      numbers[k] = rightnums[j] 
      j = j + 1

분석

Merge-Sort의 실행 시간은 다음과 같습니다. T(n). 그 후,

$ T (n) = \ begin {cases} c & if \ : n \ leqslant 1 \\ 2 \ : x \ : T (\ frac {n} {2}) + d \ : x \ : n & 그렇지 않으면 \ end {cases} $ 여기서 c 와 d 는 상수입니다.

따라서이 반복 관계를 사용하면

$$ T (n) = 2 ^ i T (\ frac {n} {2 ^ i}) + idn $$

$ i = log \ : n, \ : T (n) = 2 ^ {log \ : n} T (\ frac {n} {2 ^ {log \ : n}}) + log \ : ndn $

$ = \ : cn + dnlog \ : n $

따라서 $ T (n) = O (n \ : log \ : n) $

예

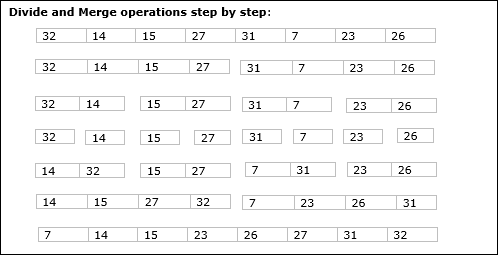
다음 예에서는 Merge-Sort 알고리즘을 단계별로 보여주었습니다. 첫째, 모든 반복 배열은 하위 배열에 하나의 요소 만 포함될 때까지 두 개의 하위 배열로 나뉩니다. 이러한 하위 배열을 더 이상 분할 할 수없는 경우 병합 작업이 수행됩니다.