DAA-최적 비용 이진 검색 트리

이진 검색 트리 (BST)는 키 값이 내부 노드에 저장되는 트리입니다. 외부 노드는 널 노드입니다. 키는 사전 순으로 정렬됩니다. 즉, 각 내부 노드에 대해 왼쪽 하위 트리의 모든 키가 노드의 키보다 적고 오른쪽 하위 트리의 모든 키가 더 큽니다.

각 키를 검색하는 빈도를 알면 트리의 각 노드에 액세스하는 데 예상되는 비용을 계산하기가 매우 쉽습니다. 최적의 이진 검색 트리는 BST로, 각 노드를 찾는 데 예상되는 최소 비용이 있습니다.

BST에서 요소의 검색 시간은 다음과 같습니다. O(n)반면 Balanced-BST 검색 시간은 O(log n). 검색 시간은 최적 비용 이진 검색 트리에서 개선 될 수 있습니다. 가장 자주 사용되는 데이터는 루트에 배치하고 루트 요소에 더 가깝게 배치하고 가장 자주 사용하지 않는 데이터는 잎과 잎에 배치합니다.

여기에서는 최적 이진 검색 트리 알고리즘이 제시됩니다. 먼저, 제공된 세트에서 BST를 구축합니다.n 고유 키 수 < k₁, k₂, k₃, ... k_n >. 여기서 우리는 키에 액세스 할 확률이K_i 이다 p_i. 일부 더미 키 (d₀, d₁, d₂, ... d_n) 키 세트에없는 값에 대해 일부 검색이 수행 될 수 있으므로 추가됩니다. K. 우리는 각 더미 키에 대해d_i 접근 가능성은 q_i.

Optimal-Binary-Search-Tree(p, q, n) 
e[1…n + 1, 0…n],  
w[1…n + 1, 0…n], 
root[1…n + 1, 0…n]  
for i = 1 to n + 1 do 
   e[i, i - 1] := qi - 1 
   w[i, i - 1] := qi - 1  
for l = 1 to n do 
   for i = 1 to n – l + 1 do 
      j = i + l – 1 e[i, j] := ∞ 
      w[i, i] := w[i, i -1] + pj + qj 
      for r = i to j do 
         t := e[i, r - 1] + e[r + 1, j] + w[i, j] 
         if t < e[i, j] 
            e[i, j] := t 
            root[i, j] := r 
return e and root

분석

알고리즘에는 O (n³) 시간, 세 중첩 이후 for루프가 사용됩니다. 이러한 각 루프는 최대n 가치.

예

다음 트리를 고려할 때 비용은 2.80이지만 최적의 결과는 아닙니다.

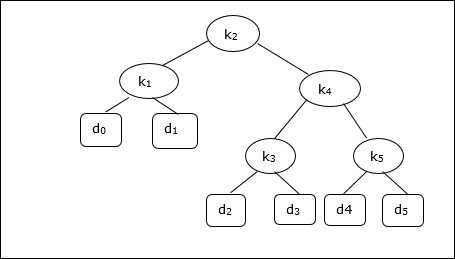
마디	깊이	개연성	기부
k 1	1	0.15	0.30
k 2	0	0.10	0.10
k 3	2	0.05	0.15
k 4	1	0.10	0.20
k 5	2	0.20	0.60
d 0	2	0.05	0.15
d 1	2	0.10	0.30
d 2	삼	0.05	0.20
d 3	삼	0.05	0.20
d 4	삼	0.05	0.20
d 5	삼	0.10	0.40
Total			2.80

최적의 솔루션을 얻기 위해이 장에서 설명하는 알고리즘을 사용하여 다음 표가 생성됩니다.

다음 표에서 열 인덱스는 i 행 인덱스는 j.

이자형	1	2	삼	4	5	6
5	2.75	2.00	1.30	0.90	0.50	0.10
4	1.75	1.20	0.60	0.30	0.05
삼	1.25	0.70	0.25	0.05
2	0.90	0.40	0.05
1	0.45	0.10
0	0.05

w	1	2	삼	4	5	6
5	1.00	0.80	0.60	0.50	0.35	0.10
4	0.70	0.50	0.30	0.20	0.05
삼	0.55	0.35	0.15	0.05
2	0.45	0.25	0.05
1	0.30	0.10
0	0.05

뿌리	1	2	삼	4	5
5	2	4	5	5	5
4	2	2	4	4
삼	2	2	삼
2	1	2
1	1

이 테이블에서 최적의 트리를 형성 할 수 있습니다.