DAA-버텍스 커버
무 방향 그래프의 정점 커버 G = (V, E) 정점의 하위 집합입니다. V' ⊆ V 그런 경우 가장자리 (u, v) 의 가장자리입니다 G, 다음 중 하나 u 에 V 또는 v 에 V' 아니면 둘다.
주어진 무 방향 그래프에서 최대 크기의 정점 커버를 찾습니다. 이 최적의 vertexcover는 NP-complete 문제의 최적화 버전입니다. 그러나 최적에 가까운 정점 커버를 찾는 것은 그리 어렵지 않습니다.
APPROX-VERTEX_COVER (G: Graph) c ← { } E' ← E[G]
while E' is not empty do
Let (u, v) be an arbitrary edge of E' c ← c U {u, v}
Remove from E' every edge incident on either u or v
return c예
주어진 그래프의 가장자리 집합은 다음과 같습니다.
{(1,6),(1,2),(1,4),(2,3),(2,4),(6,7),(4,7),(7,8),(3,8),(3,5),(8,5)}
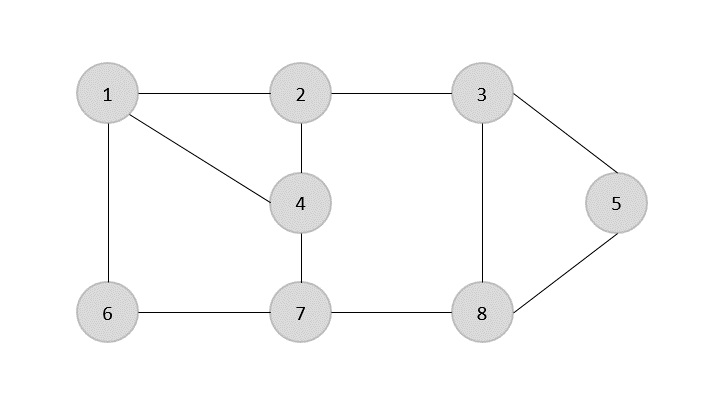
이제 임의의 가장자리 (1,6)를 선택하여 시작합니다. 정점 1 또는 6에 입사하는 모든 모서리를 제거하고 덮기 위해 모서리 (1,6)를 추가합니다.
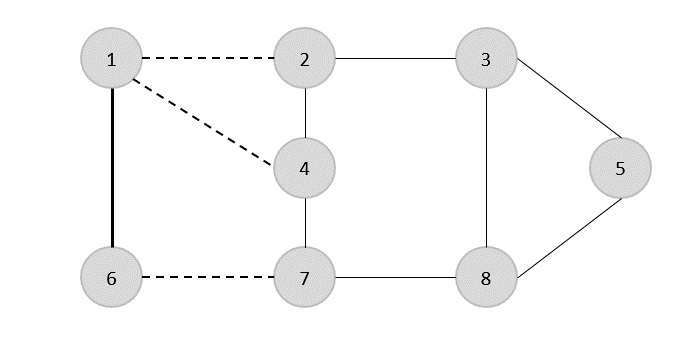
다음 단계에서는 무작위로 다른 모서리 (2,3)를 선택했습니다.
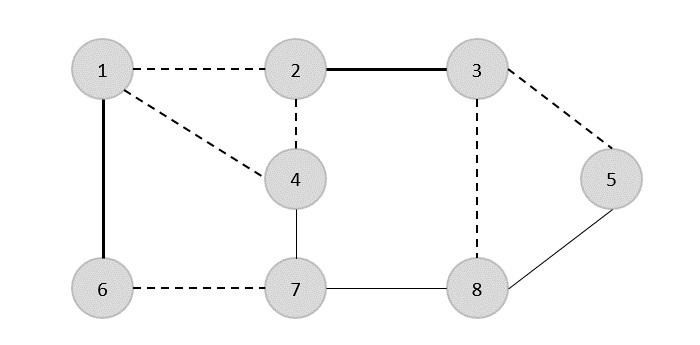
이제 다른 모서리 (4,7)를 선택합니다.
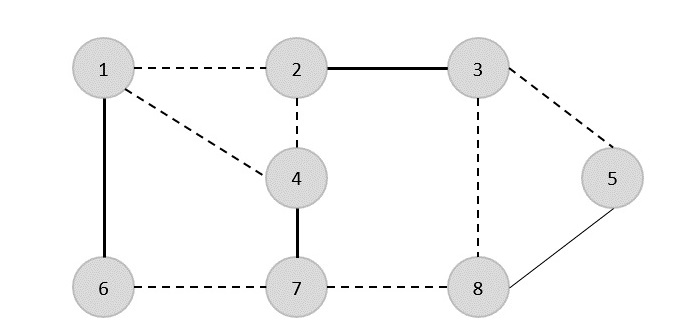
다른 모서리 (8,5)를 선택합니다.
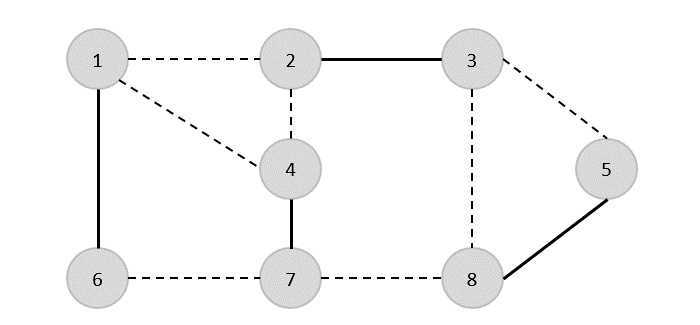
따라서이 그래프의 정점 커버는 {1,2,4,5}입니다.
분석
이 알고리즘의 실행 시간이 O(V + E), 인접 목록을 사용하여 E'.