DAA-최적의 병합 패턴
길이가 다른 정렬 된 파일 세트를 하나의 정렬 된 파일로 병합합니다. 결과 파일이 최소 시간에 생성되는 최적의 솔루션을 찾아야합니다.
정렬 된 파일의 수를 지정하면 여러 가지 방법으로 하나의 정렬 된 파일로 병합 할 수 있습니다. 이 병합은 쌍으로 수행 할 수 있습니다. 따라서 이러한 유형의 병합을 다음과 같이 호출합니다.2-way merge patterns.
페어링마다 다른 시간이 필요하므로이 전략에서는 여러 파일을 함께 병합하는 최적의 방법을 결정하려고합니다. 각 단계에서 가장 짧은 시퀀스 두 개가 병합됩니다.
병합하려면 p-record file 그리고 q-record file 아마도 필요하다 p + q 레코드 이동, 분명한 선택은 각 단계에서 가장 작은 두 파일을 병합하는 것입니다.
양방향 병합 패턴은 이진 병합 트리로 나타낼 수 있습니다. 일련의n 정렬 된 파일 {f1, f2, f3, …, fn}. 처음에 이것의 각 요소는 단일 노드 이진 트리로 간주됩니다. 이 최적의 솔루션을 찾기 위해 다음 알고리즘이 사용됩니다.
Algorithm: TREE (n)
for i := 1 to n – 1 do
declare new node
node.leftchild := least (list)
node.rightchild := least (list)
node.weight) := ((node.leftchild).weight) + ((node.rightchild).weight)
insert (list, node);
return least (list);이 알고리즘의 끝에서 루트 노드의 가중치는 최적의 비용을 나타냅니다.
예
주어진 파일 f 1 , f 2 , f 3 , f 4 및 f 5 를 각각 20, 30, 10, 5 및 30 개의 요소로 고려해 보겠습니다 .
제공된 순서에 따라 병합 작업을 수행하면
M1 = merge f1 and f2 => 20 + 30 = 50
M2 = merge M1 and f3 => 50 + 10 = 60
M3 = merge M2 and f4 => 60 + 5 = 65
M4 = merge M3 and f5 => 65 + 30 = 95
따라서 총 작업 수는
50 + 60 + 65 + 95 = 270
이제 더 나은 해결책이 있습니까?
오름차순으로 크기에 따라 숫자를 정렬하면 다음과 같은 순서를 얻습니다.
f4, f3, f1, f2, f5
따라서이 시퀀스에서 병합 작업을 수행 할 수 있습니다.
M1 = merge f4 and f3 => 5 + 10 = 15
M2 = merge M1 and f1 => 15 + 20 = 35
M3 = merge M2 and f2 => 35 + 30 = 65
M4 = merge M3 and f5 => 65 + 30 = 95
따라서 총 작업 수는
15 + 35 + 65 + 95 = 210
분명히 이것은 이전보다 낫습니다.
이 맥락에서 우리는 이제이 알고리즘을 사용하여 문제를 풀 것입니다.
초기 설정

1 단계
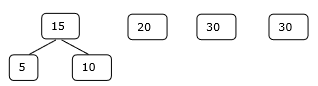
2 단계
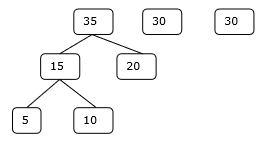
3 단계
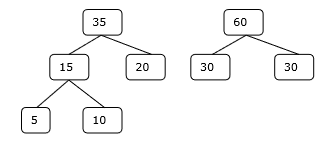
4 단계
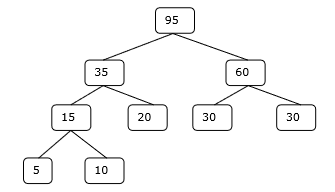
따라서 솔루션은 15 + 35 + 60 + 95 = 205 번의 비교를 사용합니다.