DAA-최단 경로

Dijkstra의 알고리즘

Dijkstra의 알고리즘 은 모든 간선이 음이 아닌 방향성 가중치 그래프 G = (V, E) 에서 단일 소스 최단 경로 문제를 해결합니다 (즉, 각 간선에 대해 w (u, v) ≥ 0 (u, v ) Є E ).

다음 알고리즘에서는 하나의 함수를 사용합니다. Extract-Min(), 키가 가장 작은 노드를 추출합니다.

Algorithm: Dijkstra’s-Algorithm (G, w, s) 
for each vertex v Є G.V  
   v.d := ∞ 
   v.∏ := NIL 
s.d := 0 
S := Ф 
Q := G.V 
while Q ≠ Ф 
   u := Extract-Min (Q) 
   S := S U {u} 
   for each vertex v Є G.adj[u] 
      if v.d > u.d + w(u, v) 
         v.d := u.d + w(u, v) 
         v.∏ := u

분석

이 알고리즘의 복잡성은 Extract-Min 함수의 구현에 전적으로 의존합니다. 최소 추출 함수가 선형 검색을 사용하여 구현 된 경우이 알고리즘의 복잡성은 다음과 같습니다.O(V² + E).

이 알고리즘에서 최소 힙을 사용하면 Extract-Min() 함수는 노드를 반환하도록 작동합니다. Q 가장 작은 키를 사용하면이 알고리즘의 복잡성을 더 줄일 수 있습니다.

예

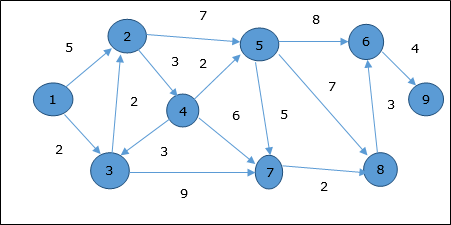
정점을 고려합시다 1 과 9각각 시작 및 대상 정점으로. 처음에 시작 정점을 제외한 모든 정점은 ∞로 표시되고 시작 정점은0.

꼭지점	머리 글자	Step1 V 1	2 단계 V 3	Step3 V 2	4 단계 V 4	5 단계 V (5)	Step6 V 7	Step7 V 8	Step8 V 6
1	0	0	0	0	0	0	0	0	0
2	∞	5	4	4	4	4	4	4	4
삼	∞	2	2	2	2	2	2	2	2
4	∞	∞	∞	7	7	7	7	7	7
5	∞	∞	∞	11	9	9	9	9	9
6	∞	∞	∞	∞	∞	17	17	16	16
7	∞	∞	11	11	11	11	11	11	11
8	∞	∞	∞	∞	∞	16	13	13	13
9	∞	∞	∞	∞	∞	∞	∞	∞	20

따라서 정점의 최소 거리 9 정점에서 1 이다 20. 그리고 경로는

1 → 3 → 7 → 8 → 6 → 9

이 경로는 선행 정보를 기반으로 결정됩니다.

Bellman Ford 알고리즘

이 알고리즘은 유 방향 그래프의 단일 소스 최단 경로 문제를 해결합니다. G = (V, E)가장자리 가중치가 음수 일 수 있습니다. 또한 음의 가중치주기가없는 경우이 알고리즘을 적용하여 최단 경로를 찾을 수 있습니다.

Algorithm: Bellman-Ford-Algorithm (G, w, s) 
for each vertex v Є G.V  
   v.d := ∞ 
   v.∏ := NIL 
s.d := 0 
for i = 1 to |G.V| - 1 
   for each edge (u, v) Є G.E 
      if v.d > u.d + w(u, v) 
         v.d := u.d +w(u, v) 
         v.∏ := u 
for each edge (u, v) Є G.E 
   if v.d > u.d + w(u, v) 
      return FALSE 
return TRUE

분석

첫번째 for 루프는 초기화에 사용되며 O(V)타임스. 다음for 루프 실행 |V - 1| 가장자리를 통과합니다.O(E) 타임스.

따라서 Bellman-Ford 알고리즘은 O(V, E) 시각.

예

다음 예제는 Bellman-Ford 알고리즘이 단계별로 작동하는 방식을 보여줍니다. 이 그래프에는 음의 에지가 있지만 음의주기가 없으므로이 기술을 사용하여 문제를 해결할 수 있습니다.

초기화시 소스를 제외한 모든 정점은 ∞로 표시되고 소스는 0.

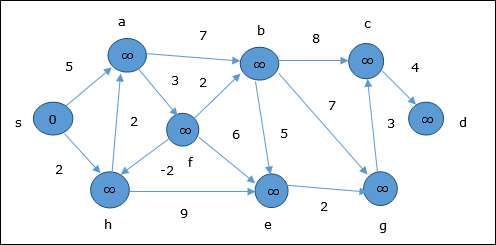
첫 번째 단계에서는 소스에서 도달 할 수있는 모든 정점이 최소 비용으로 업데이트됩니다. 따라서 정점a 과 h 업데이트됩니다.

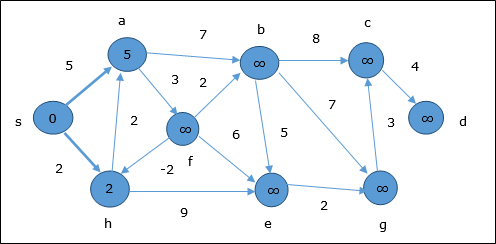
다음 단계에서 정점 a, b, f 과 e 업데이트됩니다.

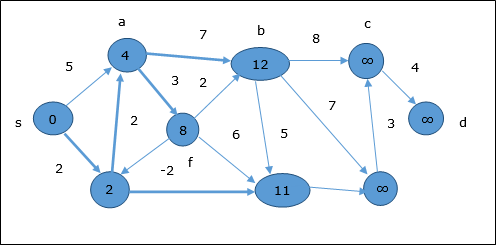
동일한 논리에 따라이 단계에서 정점 b, f, c 과 g 업데이트됩니다.

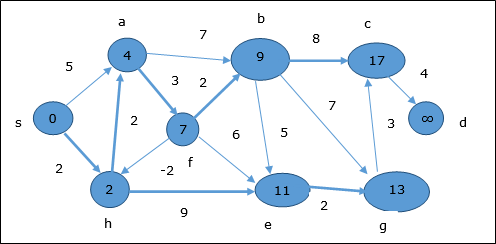
여기, 정점 c 과 d 업데이트됩니다.

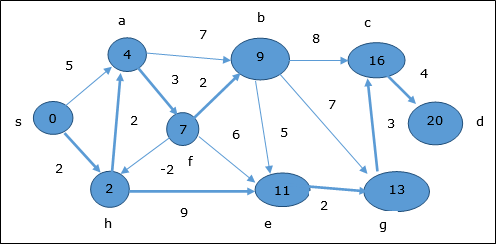
따라서 정점 사이의 최소 거리 s 및 정점 d 이다 20.

이전 정보에 따르면 경로는 s → h → e → g → c → d입니다.