AC 브리지
이 장에서는 인덕턴스를 측정하는 데 사용할 수있는 AC 브리지에 대해 설명합니다. AC 브리지는 AC 전압 신호로만 작동합니다. 그만큼circuit diagram AC 브리지의 구성은 아래 그림과 같습니다.
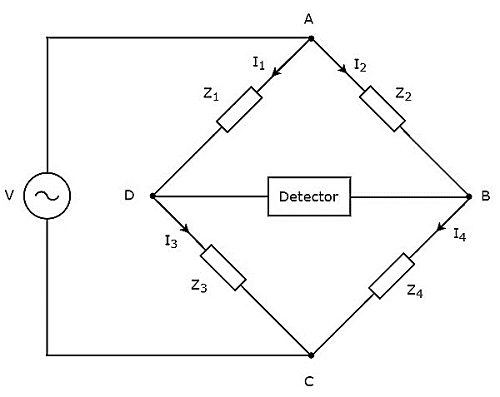
위의 그림과 같이 AC 브리지는 주로 4 개의 암으로 구성되며 마름모 또는 square shape. 이 모든 암은 임피던스로 구성됩니다.
알 수없는 임피던스 값을 찾으려면 감지기와 AC 전압 소스도 필요합니다. 따라서이 두 개 중 하나는 AC 브리지의 한 대각선에 배치되고 다른 하나는 AC 브리지의 다른 대각선에 배치됩니다. 휘트 스톤 다리의 균형 상태는-
$$ R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $$
우리는 얻을 것입니다 balancing condition of AC bridge, 위 방정식에서 R을 Z로 바꾸면됩니다.
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$ \ Rightarrow Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $
여기서 $ Z_ {1} $ 및 $ Z_ {2} $는 고정 임피던스입니다. 반면 $ Z_ {3} $는 표준 가변 임피던스이고 $ Z_ {4} $는 알 수없는 임피던스입니다.
Note −이 4 가지 임피던스 중 두 가지를 고정 임피던스로 선택할 수 있습니다. 하나는 표준 가변 임피던스로, 다른 하나는 알 수없는 임피던스로 애플리케이션에 따라 선택할 수 있습니다.
다음은 측정에 사용할 수있는 두 개의 AC 브리지입니다. inductance.
- 맥스웰의 다리
- 헤이즈 브리지
이제이 두 AC 브리지에 대해 하나씩 살펴 보겠습니다.
맥스웰의 다리
Maxwell의 브리지는 4 개의 암이있는 AC 브리지로, 마름모 또는 square shape. 이 브리지의 두 암은 단일 저항으로 구성되고 한 암은 저항과 인덕터의 직렬 조합으로 구성되고 다른 암은 저항과 커패시터의 병렬 조합으로 구성됩니다.
알 수없는 임피던스 값을 찾기 위해 AC 검출기와 AC 전압 소스가 사용됩니다. 따라서이 두 개 중 하나는 Maxwell 다리의 대각선 하나에 배치되고 다른 하나는 Maxwell 다리의 다른 대각선에 배치됩니다.
Maxwell의 브리지는 중간 인덕턴스 값을 측정하는 데 사용됩니다. 그만큼circuit diagram Maxwell의 다리는 아래 그림과 같습니다.
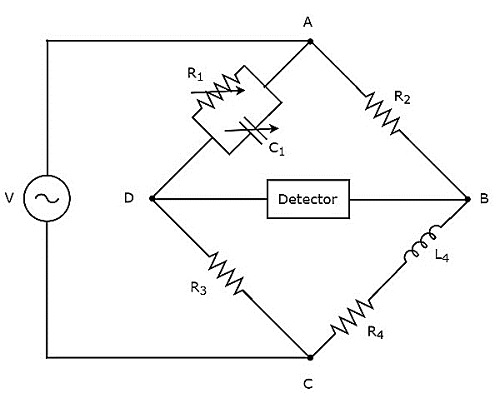
위의 회로에서 암 AB, BC, CD 및 DA는 함께 마름모 또는 정사각형 모양을 형성합니다. 암 AB와 CD는 각각 $ R_ {2} $ 및 $ R_ {3} $ 저항으로 구성됩니다. 암 BC는 저항 $ R_ {4} $와 인덕터 $ L_ {4} $의 직렬 조합으로 구성됩니다. 암, DA는 저항기 $ R_ {1} $ 및 커패시터 $ C_ {1} $의 병렬 조합으로 구성됩니다.
$ Z_ {1}, Z_ {2}, Z_ {3} $ 및 $ Z_ {4} $가 각각 암 DA, AB, CD 및 BC의 임피던스라고합시다. 그만큼values of these impedances 될거야
$$ Z_ {1} = \ frac {R_ {1} \ left (\ frac {1} {j \ omega C_ {1}} \ right)} {R_ {1} + \ frac {1} {j \ omega C_ {1}}} $$
$$ \ Rightarrow Z_ {1} = \ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}} $$
$ Z_ {2} = R_ {2} $
$ Z_ {3} = R_ {3} $
$ Z_ {4} = R_ {4} + j \ omega L_ {4} $
Substitute AC 브리지의 다음 균형 상태에서 이러한 임피던스 값.
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ 왼쪽 ({\ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}} \ 오른쪽)} $$
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} \ left (1 + j \ omega R_ {1} C_ {1} \ right)} {R_ { 1}} $
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + \ frac {j \ omega R_ {1} C_ {1} R_ {2} R_ {3}} {R_ {1}} $
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + j \ omega C_ {1} R_ {2} R_ {3} $
으로 comparing 위 방정식의 각각의 실수 및 허수 항, 우리는
$ R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $ 방정식 1
$ L_ {4} = C_ {1} R_ {2} R_ {3} $ 방정식 2
방정식 1에서 저항기 $ R_ {1} $, $ R_ {2} $ 및 $ R_ {3} $의 값을 대체하여 저항기 $ R_ {4} $의 값을 얻습니다. 마찬가지로 방정식 2에서 커패시터 값 $ C_ {1} $와 저항 값 $ R_ {2} $ 및 $ R_ {3} $를 대입하여 인덕터 값 $ L_ {4를 얻습니다. } $.
그만큼 advantage Maxwell의 브리지에서 저항 값 $ R_ {4} $와 인덕터 $ L_ {4} $는 주파수 값과 무관하다는 것입니다.
헤이즈 브리지
Hay 's bridge는 Maxwell 브리지의 수정 된 버전으로, Maxwell 브리지의 저항과 커패시터의 직렬 조합으로 구성된 저항과 커패시터의 병렬 조합으로 구성된 암을 수정하여 얻습니다.
Hay 's bridge는 높은 인덕턴스 값을 측정하는 데 사용됩니다. 그만큼circuit diagram Hay 's bridge의 모습은 아래 그림과 같습니다.
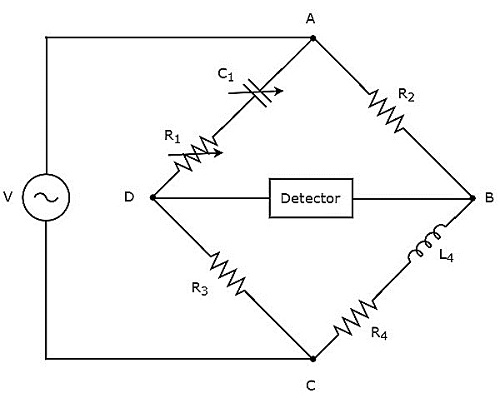
위의 회로에서 암 AB, BC, CD 및 DA는 함께 마름모 또는 정사각형 모양을 형성합니다. 암, AB 및 CD는 각각 $ R_ {2} $ 및 $ R_ {3} $ 저항으로 구성됩니다. 암 BC는 저항 $ R_ {4} $와 인덕터 $ L_ {4} $의 직렬 조합으로 구성됩니다. 팔, DA는 저항기 $ R_ {1} $ 및 커패시터 $ C_ {1} $의 직렬 조합으로 구성됩니다.
$ Z_ {1}, Z_ {2}, Z_ {3} $ 및 $ Z_ {4} $가 각각 암 DA, AB, CD 및 BC의 임피던스라고합시다. 그만큼values of these impedances 될거야
$$ Z_ {1} = R_ {1} + \ frac {1} {j \ omega C_ {1}} $$
$ \ Rightarrow Z_ {1} = \ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} $
$ Z_ {2} = R_ {2} $
$ Z_ {3} = R_ {3} $
$ Z_ {4} = R_ {4} + j \ omega L_ {4} $
Substitute AC 브리지의 다음 균형 상태에서 이러한 임피던스 값.
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ left (\ frac {1 + j \ omega R_ {1} C_ {1}} {j \ 오메가 C_ {1}} \ 오른쪽)} $
$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ left (1 + j \ omega R_ {1} C_ {1} \ 오른쪽)} $
위 방정식의 우변 항의 분자와 분모에 $ 1-j \ omega R_ {1} C_ {1} $를 곱합니다.
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ left (1 + j \ omega R_ {1} C_ { 1} \ right)} \ times \ frac {\ left (1-j \ omega R_ {1} C_ {1} \ right)} {\ left (1-j \ omega R_ {1} C_ {1} \ right )} $
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3} + j \ 오메가 R_ {2} R_ {3} C_ {1}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} $
으로 comparing 위 방정식의 각각의 실수 및 허수 항, 우리는
$ R_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} $ 방정식 3
$ L_ {4} = \ frac {R_ {2} R_ {3} C_ {1}} {\ 왼쪽 (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} $ 방정식 4
방정식 3과 방정식 4에서 $ R_ {1}, R_ {2}, R_ {3}, C_ {1} $ 및 $ \ omega $의 값을 대체하여 저항기 $ R_ {4의 값을 얻습니다. } $ 및 인덕터, $ L_ {4} $.