Lissajous 피규어
Lissajous figureCRO의 수평 및 수직 편향 판 모두에 사인파 신호가 적용될 때 화면에 표시되는 패턴입니다. 이러한 패턴은 CRO의 수평 및 수직 편향 플레이트 모두에 적용되는 정현파 신호의 진폭, 주파수 및 위상차에 따라 달라집니다.
다음 그림은 example Lissajous 그림의.
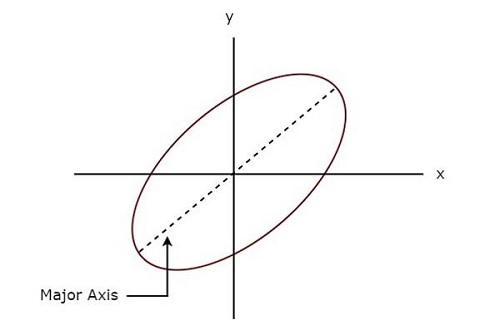
위의 Lissajous 그림은 elliptical shape 장축은 양의 x 축과 약간의 경사각을 가지고 있습니다.
Lissajous Figure를 사용한 측정
우리는 다음을 할 수 있습니다 two measurements Lissajous 그림에서.
- 정현파 신호의 주파수
- 두 정현파 신호 간의 위상차
이제이 두 측정에 대해 하나씩 논의 해 보겠습니다.
주파수 측정
CRO의 수평 및 수직 편향 판 모두에 사인파 신호가 적용되면 Lissajous 그림이 화면에 표시됩니다. 따라서 표준이있는 정현파 신호를 적용합니다.known frequencyCRO의 수평 편향 판에. 마찬가지로 사인파 신호를 적용합니다.frequency 이다 unknown CRO의 수직 편향 판에
$ f_ {H} $ 및 $ f_ {V} $는 CRO의 수평 및 수직 편향 판에 각각 적용되는 사인파 신호의 주파수입니다. $ f_ {H} $와 $ f_ {V} $의 관계는 다음과 같습니다.mathematically 아래와 같이 표현됩니다.
$$ \ frac {f_ {V}} {f_ {H}} = \ frac {n_ {H}} {n_ {V}} $$
위의 관계에서 우리는 CRO의 수직 편향 판에 적용되는 정현파 신호의 주파수를 얻을 수 있습니다.
$ f_ {V} = \ left (\ frac {n_ {H}} {n_ {V}} \ right) f_ {H} $ (수식 1)
어디,
$ n_ {H} $는 수평 접선의 수입니다.
$ n_ {V} $는 수직 접선의 수입니다.
Lissajous 그림에서 $ n_ {H} $ 및 $ n_ {V} $의 값을 찾을 수 있습니다. 따라서 방정식 1에서 $ n_ {H} $, $ n_ {V} $ 및 $ f_ {H} $의 값을 대체하여 다음 값을 얻습니다.$f_{V}$, 즉 frequency of sinusoidal signal CRO의 수직 편향 판에 적용됩니다.
위상차 측정
CRO의 수평 및 수직 편향 판 모두에 사인파 신호가 적용되면 Lissajous 그림이 화면에 표시됩니다. 따라서 정현파 신호를 적용하십시오.same amplitude and frequency CRO의 수평 및 수직 편향 판 모두에.
모양을 기반으로 한 일부 Lissajous 그림의 경우 두 정현파 신호 간의 위상 차이를 직접 알 수 있습니다.
Lissajous 그림이 straight line 양의 x 축에 $ 45 ^ {\ circ} $ 경사면 phase difference두 정현파 신호 사이는 $ 0 ^ {\ circ} $가됩니다. 즉, 두 정현파 신호간에 위상차가 없습니다.
Lissajous 그림이 straight line 양의 x 축에 $ 135 ^ {\ circ} $ 경사면 phase difference두 정현파 신호 사이에는 $ 180 ^ {\ circ} $가됩니다. 즉,이 두 정현파 신호는 위상이 맞지 않습니다.
Lissajous 그림이 circular shape, 그러면 두 정현파 신호 간의 위상차는 $ 90 ^ {\ circ} $ 또는 $ 270 ^ {\ circ} $가됩니다.
Lissajous 수치가 다음과 같을 때 공식을 사용하여 두 정현파 신호 간의 위상차를 계산할 수 있습니다. elliptical shape.
경사각이있는 타원형 Lissajous 도형의 장축이 양의 x 축으로 $ 0 ^ {\ circ} $와 $ 90 ^ {\ circ} $ 사이에 있으면 두 정현파 신호의 위상차가됩니다.
$$ \ phi = \ sin ^ {-1} \ left (\ frac {x_ {1}} {x_ {2}} \ right) = \ sin ^ {-1} \ left (\ frac {y_ {1} } {y_ {2}} \ 오른쪽) $$
경사각이있는 타원형 Lissajous 도형의 장축이 양의 x 축으로 $ 90 ^ {\ circ} $에서 $ 180 ^ {\ circ} $ 사이에 있으면 두 정현파 신호의 위상차가됩니다.
$$ \ phi = 180-\ sin ^ {-1} \ left (\ frac {x_ {1}} {x_ {2}} \ right) = 180-\ sin ^ {-1} \ left (\ frac { y_ {1}} {y_ {2}} \ 오른쪽) $$
Where,
$ x_ {1} $는 원점에서 x 축 점까지의 거리이며, 여기서 타원형 Lissajous 그림이 교차합니다.
$ x_ {2} $는 원점에서 타원형 Lissajous 그림의 수직 접선까지의 거리입니다.
$ y_ {1} $는 원점에서 Y 축의 점까지의 거리이며, 여기서 타원형 Lissajous 그림이 교차합니다.
$ y_ {2} $는 원점에서 타원형 Lissajous 그림의 수평 접선까지의 거리입니다.
이 장에서는 공식을 사용하여 Lissajous 그림에서 두 개의 정현파 신호 간의 미지 정현파 신호의 주파수와 위상차를 찾는 방법을 배웠습니다.