빠른 가이드
수량을 측정하는 데 사용되는 기기를 측정 기기라고합니다. 이 튜토리얼은 주로electronic instruments, 전기량 또는 매개 변수를 측정하는 데 유용합니다.
다음은 가장 일반적으로 사용되는 전자 기기입니다.
- Voltmeter
- Ammeter
- Ohmmeter
- Multimeter
이제 이러한 도구에 대해 간략하게 논의하겠습니다.
전압계
이름에서 알 수 있듯이 voltmeter전기 회로의 두 지점에서 전압을 측정하는 측정 장비입니다. 전압계에는 DC 전압계와 AC 전압계의 두 가지 유형이 있습니다.
DC 전압계는 전기 회로의 두 지점에서 DC 전압을 측정하는 반면, AC 전압계는 전기 회로의 두 지점에서 AC 전압을 측정합니다. 예practical DC voltmeter 아래 그림에 나와 있습니다.

위 그림에 표시된 DC 전압계는 $(0-100)V$ DC voltmeter. 따라서 0V에서 10V까지의 DC 전압을 측정하는 데 사용할 수 있습니다.
전류계
이름에서 알 수 있듯이 ammeter전기 회로의 두 지점을 통해 흐르는 전류를 측정하는 측정기입니다. 전류계에는 DC 전류계와 AC 전류계의 두 가지 유형이 있습니다.
DC 전류계는 전기 회로의 두 지점을 통해 흐르는 DC 전류를 측정합니다. 반면 AC 전류계는 전기 회로의 두 지점을 통해 흐르는 AC 전류를 측정합니다. 예practical AC ammeter 아래 그림에 나와 있습니다-

위 그림에 표시된 AC 전류계는 $(0-100)A \:$ AC ammeter. 따라서 0A에서 100A까지의 AC 전류를 측정하는 데 사용할 수 있습니다.
저항계
Ohmmeter전기 회로의 두 지점 사이의 저항 값을 측정하는 데 사용됩니다. 알 수없는 저항의 값을 찾는데도 사용할 수 있습니다. 저항계에는 직렬 저항계와 션트 저항계의 두 가지 유형이 있습니다.
직렬 형 저항계에서는 값을 알 수없고 측정 할 저항을 저항계와 직렬로 연결해야합니다. 측정에 유용합니다high values of resistances.

션트 형 저항계에서는 값을 알 수없고 측정 할 저항을 저항계와 병렬 (분로)로 연결해야합니다. 측정에 유용합니다low values of resistances.
예 practical shunt ohmmeter위 그림에 나와 있습니다. 위 그림에 표시된 저항계는$(0-100)\Omega$ shunt ohmmeter. 따라서 0 옴에서 100 옴까지 저항 값을 측정하는 데 사용할 수 있습니다.
멀티 미터
Multimeter전압, 전류 및 저항과 같은 양을 한 번에 하나씩 측정하는 데 사용되는 전자 기기입니다. DC 및 AC 전압, DC 및 AC 전류 및 여러 범위의 저항을 측정하는 데 사용할 수 있습니다. 실제 멀티 미터는 다음 그림에 나와 있습니다.

그림과 같이이 멀티 미터는 다양한 고 저항, 저 저항, DC 전압, AC 전압, DC 전류 및 AC 전류를 측정하는 데 사용할 수 있습니다. 이러한 각 수량에 대한 다양한 스케일 및 값 범위가 위 그림에 표시되어 있습니다.
이 장에서 고려한 도구는 indicating type instruments, 이러한 악기의 포인터가 특정 값을 가리키고 기울이기 때문에. 이러한 전자 측정 기기에 대해서는 이후 장에서 자세히 설명합니다.
기기의 성능을 파악하고 수량이나 매개 변수를 측정하는 데 도움이되는 측정 기기의 특성은 다음과 같이 알려져 있습니다. Performance Characteristics.
성능 특성의 유형
악기의 성능 특성은 다음과 같이 분류 할 수 있습니다. two types.
- 정적 특성
- 동적 특성
이제이 두 가지 유형의 특성에 대해 하나씩 살펴 보겠습니다.
정적 특성
수량 또는 매개 변수 측정 장비의 특성 do not vary시간과 관련하여 정적 특성이라고합니다. 때로는 이러한 양이나 매개 변수가 시간에 따라 느리게 변할 수 있습니다. 다음은 목록입니다static characteristics.
- Accuracy
- Precision
- Sensitivity
- Resolution
- 정적 오류
이제 이러한 정적 특성에 대해 하나씩 논의 해 보겠습니다.
정확성
악기의 표시된 값 $ A_ {i} $와 실제 값 $ A_ {t} $ 간의 대수적 차이는 다음과 같습니다. accuracy. 수학적으로 다음과 같이 나타낼 수 있습니다.
$$ Accuracy = A_ {i}-A_ {t} $$
정확도라는 용어는 악기의 표시된 값 $ A_ {i} $가 실제 값 $ A_ {t} $에 얼마나 가까운지를 나타냅니다.
정적 오류
시간에 따라 변하지 않는 수량의 실제 가치 $ A_ {t} $와 상품의 표시된 가치 $ A_ {i} $의 차이는 다음과 같습니다. static error, $ e_ {s} $. 수학적으로 다음과 같이 나타낼 수 있습니다.
$$ e_ {s} = A_ {t}-A_ {i} $$
정적 오류라는 용어는 기기의 부정확성을 나타냅니다. 정적 오류가 백분율로 표시되면 다음과 같이 호출됩니다.percentage of static error. 수학적으로 다음과 같이 나타낼 수 있습니다.
$$ \ % e_ {s} = \ frac {e_ {s}} {A_ {t}} \ times 100 $$
위 방정식의 오른쪽에있는 $ e_ {s} $ 값을 대입합니다.
$$ \ % e_ {s} = \ frac {A_ {t}-A_ {i}} {A_ {t}} \ times 100 $$
어디,
$ \ % e_ {s} $는 정적 오류의 백분율입니다.
정도
같은 상황에서 같은 양을 여러 번 측정하는 데 사용했을 때 같은 값을 반복적으로 표시하는 기기는 precision.
감광도
측정 할 입력의 주어진 변화에 대한 계측기의 출력 변화율 $ \ Delta A_ {out} $, $ \ Delta A_ {in} $가 호출됩니다. sensitivity, S. 수학적으로 다음과 같이 나타낼 수 있습니다.
$$ S = \ frac {\ Delta A_ {out}} {\ Delta A_ {in}} $$
민감도 라는 용어 는 계측기가 응답하는 데 필요한 측정 가능한 입력의 가장 작은 변화를 의미합니다.
교정 곡선이 linear, 기기의 감도는 일정하고 교정 곡선의 기울기와 같습니다.
교정 곡선이 non-linear, 악기의 감도가 일정하지 않고 입력에 따라 달라집니다.
해결
계측기의 출력이 특정 입력 증가가있을 때만 변경되는 경우 해당 입력 증가가 호출됩니다. Resolution. 즉, 기기는 입력 해상도가있을 때 입력을 효과적으로 측정 할 수 있습니다.
동적 특성
시간에 따라 매우 빠르게 변하는 양이나 매개 변수를 측정하는 데 사용되는 기기의 특성을 동적 특성이라고합니다. 다음은 목록입니다dynamic characteristics.
- 응답 속도
- 동적 오류
- Fidelity
- Lag
이제 이러한 동적 특성에 대해 하나씩 논의 해 보겠습니다.
응답 속도
측정 할 양에 변화가있을 때마다 기기가 반응하는 속도를 호출합니다. speed of response. 기기의 속도를 나타냅니다.
지연
측정 할 양에 변화가있을 때마다 기기의 응답에 나타나는 지연 량을 측정 지연이라고합니다. 또한 간단히lag.
동적 오류
시간에 따라 달라지는 수량의 실제 값 $ A_ {t} $와 악기의 표시된 값 $ A_ {i} $ 간의 차이를 동적 오류 $ e_ {d} $라고합니다.
충실도
계측기가 동적 오류없이 측정 된 양의 변화를 나타내는 정도는 다음과 같이 알려져 있습니다. Fidelity
측정 중에 발생하는 오류는 다음과 같습니다. measurement errors. 이 장에서는 측정 오류 유형에 대해 설명합니다.
측정 오류의 유형
측정 오차는 다음과 같은 세 가지 유형으로 분류 할 수 있습니다.
- 총 오류
- 무작위 오류
- 체계적인 오류
이제이 세 가지 유형의 측정 오류에 대해 하나씩 살펴 보겠습니다.
총 오류
측정 값을 취하는 동안 관찰자의 경험 부족으로 인해 발생하는 오류를 gross errors. 총 오차 값은 관찰자마다 다릅니다. 때로는 부적절한 기기 선택으로 인해 총 오류가 발생할 수도 있습니다. 이 두 단계를 따르면 총 오류를 최소화 할 수 있습니다.
- 측정 할 값 범위에 따라 가장 적합한 기기를 선택하십시오.
- 판독 값을주의 깊게 기록하십시오.
체계적인 오류
기기에서 오류가 발생하면 작동 중에 일정한 편차가 발생하는 경우 systematic error. 기기에 사용되는 재료의 특성으로 인해 체계적인 오류가 발생합니다.
Types of Systematic Errors
체계적인 오류는 다음과 같이 분류 할 수 있습니다. three types.
Instrumental Errors − 이러한 유형의 오류는 기기의 단점과 로딩 효과로 인해 발생합니다.
Environmental Errors − 이러한 유형의 오류는 온도, 압력 등의 변화와 같은 환경 변화로 인해 발생합니다.
observational Errors − 이러한 유형의 오류는 미터 판독 값을 취하는 동안 관찰자 때문에 발생합니다. Parallax errors 이 유형의 오류에 속합니다.
무작위 오류
측정 시간 동안 알려지지 않은 원인으로 인해 발생하는 오류를 random errors. 따라서 이러한 오류를 제거하거나 최소화 할 수 없습니다. 그러나 임의의 오류없이 더 정확한 측정 값을 얻으려면 다음 두 단계를 수행하면됩니다.
Step1 − 다른 관찰자에 의해 더 많은 판독 값을 가져옵니다.
Step2 − 1 단계에서 얻은 판독 값에 대한 통계 분석을 수행합니다.
다음은 통계 분석에 사용되는 매개 변수입니다.
- Mean
- Median
- Variance
- Deviation
- 표준 편차
이제 이것들에 대해 논의합시다 statistical parameters.
평균
$ x_ {1}, x_ {2}, x_ {3}, ...., x_ {N} $를 특정 측정 값의 $ N $ 판독 값이라고합니다. 평균 또는average value 이러한 판독 값 중 다음 공식을 사용하여 계산할 수 있습니다.
$$ m = \ frac {x_ {1} + x_ {2} + x_ {3} + .... + x_ {N}} {N} $$
여기서 $ m $는 평균 또는 평균 값입니다.
특정 측정 값의 판독 수가 더 많으면 평균 또는 평균 값은 대략 다음과 같습니다. true value
중앙값
특정 측정의 판독 횟수가 더 많으면 평균 또는 평균 값을 계산하기가 어렵습니다. 여기에서median value 평균값과 거의 같습니다.
중앙값을 계산하려면 먼저 특정 측정 값의 판독 값을 ascending order. 측정 횟수가 다음과 같을 때 다음 공식을 사용하여 중앙값을 계산할 수 있습니다.odd number.
$$ M = x _ {\ 왼쪽 (\ frac {N + 1} {2} \ right)} $$
측정 횟수가 다음과 같을 때 다음 공식을 사용하여 중앙값을 계산할 수 있습니다. even number.
$$ M = \ frac {x _ {\ left (N / 2 \ right)} + x_ \ left (\ left [N / 2 \ right] +1 \ right)} {2} $$
평균 편차
특정 측정 값과 평균값 간의 차이를 평균 편차 라고 합니다. 요컨대 편차 라고 합니다. 수학적으로 다음과 같이 나타낼 수 있습니다.
$$ d_ {i} = x_ {i} ~ m $$
어디,
$ d_ {i} $는 평균값에서 $ i ^ {th} $ 판독 값의 편차입니다.
$ x_ {i} $는 $ i ^ {th} $ 독서의 가치입니다.
$ m $는 평균 또는 평균 값입니다.
표준 편차
편차의 제곱 평균은 다음과 같습니다. standard deviation. 수학적으로 다음과 같이 나타낼 수 있습니다.
$$ \ sigma = \ sqrt {\ frac {{d_ {1}} ^ {2} + {d_ {2}} ^ {2} + {d_ {3}} ^ {2} + .... + { d_ {N}} ^ {2}} {N}} $$
위의 공식은 판독 횟수 N이 20보다 크거나 같을 때 유효합니다. 판독 횟수 N이 20보다 작을 때 표준 편차에 대해 다음 공식을 사용할 수 있습니다.
$$ \ sigma = \ sqrt {\ frac {{d_ {1}} ^ {2} + {d_ {2}} ^ {2} + {d_ {3}} ^ {2} + .... + { d_ {N}} ^ {2}} {N-1}} $$
어디,
$ \ sigma $는 표준 편차입니다.
$ d_ {1}, d_ {2}, d_ {3},…, d_ {N} $는 각각 평균에서 첫 번째, 두 번째, 세 번째,…, $ N ^ {th} $ 판독 값의 편차입니다.
Note − 표준 편차 값이 작 으면 측정 값 판독 값이 더 정확 해집니다.
변화
표준 편차의 제곱은 variance. 수학적으로 다음과 같이 나타낼 수 있습니다.
$$ V = \ sigma ^ {2} $$
어디,
$ V $는 분산입니다.
$ \ sigma $는 표준 편차입니다.
평균 편차 제곱은 variance. 수학적으로 다음과 같이 나타낼 수 있습니다.
$$ V = \ frac {{d_ {1}} ^ {2} + {d_ {2}} ^ {2} + {d_ {3}} ^ {2} + .... + {d_ {N} } ^ {2}} {N} $$
위의 공식은 판독 횟수 N이 20보다 크거나 같을 때 유효합니다. 판독 횟수 N이 20보다 작을 때 분산에 다음 공식을 사용할 수 있습니다.
$$ V = \ frac {{d_ {1}} ^ {2} + {d_ {2}} ^ {2} + {d_ {3}} ^ {2} + .... + {d_ {N} } ^ {2}} {N-1} $$
어디,
$ V $는 분산입니다.
$ d_ {1}, d_ {2}, d_ {3},…, d_ {N} $는 각각 평균에서 첫 번째, 두 번째, 세 번째,…, $ N ^ {th} $ 판독 값의 편차입니다.
따라서 통계 매개 변수의 도움으로 특정 측정의 판독 값을 분석 할 수 있습니다. 이렇게하면보다 정확한 측정 값을 얻을 수 있습니다.
수량을 측정하는 데 사용되는 도구는 다음과 같습니다. measuring instruments. 기기가 전압 및 전류와 같은 기본 전기량을 측정 할 수있는 경우basic measuring instruments.
기본 측정 기기의 유형
기본 측정기는 다음 두 가지 유형으로 분류 할 수 있습니다.
- Voltmeters
- Ammeters
이 두 가지 기본 측정 장비에 대해 간략하게 설명하겠습니다.
전압계
이름에서 알 수 있듯이 voltmeter전기 회로의 두 지점에서 전압을 측정하는 측정 장비입니다. 전압의 단위는 볼트이고 측정기는 미터입니다. 따라서 "전압계"라는 단어는 두 단어를 결합하여 얻습니다.“volt” 과 “meter”.
전압계를 다음과 같이 분류 할 수 있습니다. two types 측정 할 수있는 전압 유형에 따라
- DC 전압계
- AC 전압계
DC 전압계
이름에서 알 수 있듯이 DC 전압계는 DC voltage전기 회로의 두 지점에서. 실제 DC 전압계가 아래 그림에 나와 있습니다.

그림에 표시된 DC 전압계는 $(0-10)V$ DC voltmeter. 따라서 0V에서 10V까지의 DC 전압을 측정하는 데 사용할 수 있습니다.
AC 전압계
이름에서 알 수 있듯이 AC 전압계는 AC voltage전기 회로의 두 지점에서. 실제 AC 전압계가 아래 그림에 나와 있습니다.

위 그림에 표시된 AC 전압계는 $(0-250)V$ AC voltmeter. 따라서 0V에서 250V까지의 AC 전압을 측정하는 데 사용할 수 있습니다.
전류계
이름에서 알 수 있듯이 ammeter전기 회로의 두 지점을 통해 흐르는 전류를 측정하는 측정기입니다. 전류의 단위는 암페어이고 측정기는 미터입니다. “전류계”라는 단어는“am” 암페어의 “meter”.
전류계를 다음과 같이 분류 할 수 있습니다. two types 측정 할 수있는 전류 유형을 기반으로합니다.
- DC 전류계
- AC 전류계
DC 전류계
이름에서 알 수 있듯이 DC 전류계는 DC current전기 회로의 두 지점을 통해 흐르는 실제 DC 전류계가 그림에 나와 있습니다.

위 그림에 표시된 DC 전류계는 $(0-50)A$ DC ammeter. 따라서 0A에서 50A까지의 DC 전류를 측정하는 데 사용할 수 있습니다.
AC 전류계
이름에서 알 수 있듯이 AC 전류계는 AC current전기 회로의 두 지점을 통해 흐르는 실제 AC 전류계가 아래 그림에 나와 있습니다.

위 그림에 표시된 AC 전류계는 $(0-100)A$ AC ammeter. 따라서 0A에서 100A까지의 AC 전류를 측정하는 데 사용할 수 있습니다.
다음 몇 장에서 다양한 전압계와 전류계에 대해 자세히 설명합니다.
DC 전압계는 전기 회로의 두 지점에서 DC 전압을 측정하는 데 사용되는 측정 기기입니다. PMMC (Permanent Magnet Moving Coil) 검류계와 직렬로 저항을 배치하면 전체 조합이 다음과 같이 작동합니다.DC voltmeter.
DC 전압계에 사용되는 직렬 저항은 직렬 곱셈기 저항 또는 간단히 곱셈기라고도합니다. 미터 전류가 전체 스케일 편향 값을 초과하는 것을 방지하기 위해 기본적으로 검류계를 통해 흐르는 전류의 양을 제한합니다. 그만큼circuit diagram DC 전압계의 값은 아래 그림과 같습니다.
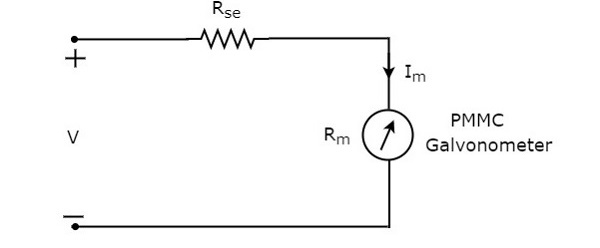
DC 전압이 측정되는 전기 회로의 두 지점에이 DC 전압계를 배치해야합니다.
대다 KVL 위 회로의 루프 주변.
$ V-I_ {m} R_ {se} -I_ {m} R_ {m} = 0 $ (수식 1)
$$ \ 오른쪽 화살표 V-I_ {m} R_ {m} = I_ {m} R_ {se} $$
$$ \ Rightarrow R_ {se} = \ frac {V-I_ {m} R_ {m}} {I_ {m}} $$
$ \ Rightarrow R_ {se} = \ frac {V} {I_ {m}}-R_ {m} $ (수식 2)
어디,
$ R_ {se} $는 계열 승수 저항입니다.
$ V $는 측정 할 전체 범위 DC 전압입니다.
$ I_ {m} $는 풀 스케일 편향 전류입니다.
$ R_ {m} $는 검류계의 내부 저항입니다.
측정 할 전체 범위 DC 전압의 비율 $ V $와 검류계의 DC 전압 강하 $ V_ {m} $는 다음과 같이 알려져 있습니다. multiplying factor, 미디엄. 수학적으로 다음과 같이 나타낼 수 있습니다.
$ m = \ frac {V} {V_ {m}} $ (수식 3)
방정식 1에서 다음 방정식을 얻습니다. full range DC voltage 즉, $ V $입니다.
$ V = I_ {m} R_ {se} + I_ {m} R_ {m} $ (수식 4)
그만큼 DC voltage drop검류계에서 $ V_ {m} $는 풀 스케일 편향 전류 $ I_ {m} $와 검류계의 내부 저항 $ R_ {m} $의 곱입니다. 수학적으로 다음과 같이 쓸 수 있습니다.
$ V_ {m} = I_ {m} R_ {m} $ (수식 5)
Substitute, 방정식 4 및 방정식 3의 방정식 5
$$ m = \ frac {I_ {m} R_ {se} + I_ {m} R_ {m}} {I_ {m} R_ {m}} $$
$ \ Rightarrow m = \ frac {R_ {se}} {R_ {m}} + 1 $
$ \ Rightarrow m-1 = \ frac {R_ {se}} {R_ {m}} $
$ R_ {se} = R_ {m} \ left (m-1 \ right) $ (수식 6)
우리는 찾을 수 있습니다 value of series multiplier resistance 사용 가능한 데이터를 기반으로 방정식 2 또는 방정식 6을 사용합니다.
다중 범위 DC 전압계
이전 섹션에서는 PMMC 검류계와 직렬로 멀티 플라이어 저항을 배치하여 얻은 DC 전압계에 대해 설명했습니다. 이 DC 전압계는particular range DC 전압의.
DC 전압계를 사용하여 DC 전압을 측정하려면 multiple ranges, 그런 다음 단일 승수 저항 대신 여러 개의 병렬 승수 저항을 사용해야하며이 저항의 전체 조합은 PMMC 검류계와 직렬로 연결됩니다. 그만큼circuit diagram 다중 범위 DC 전압계의 그림은 아래 그림과 같습니다.
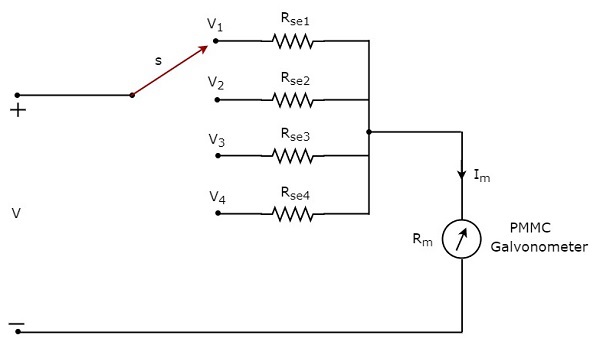
우리는 이것을 배치해야 multi range DC voltmeter필요한 범위의 DC 전압이 측정되는 전기 회로의 두 지점에 걸쳐 있습니다. 스위치 s를 각각의 곱셈기 저항에 연결하여 원하는 전압 범위를 선택할 수 있습니다.
$ m_ {1}, m_ {2}, m_ {2} $ 및 $ m_ {4} $는 multiplying factors측정 할 전체 범위 DC 전압을 각각 $ V_ {1}, V_ {2}, V_ {3} $ 및 $ V_ {4} $로 고려할 때 DC 전압계의 다음은 각 배율에 해당하는 공식입니다.
$$ m_ {1} = \ frac {V_ {1}} {V_ {m}} $$
$$ m_ {2} = \ frac {V_ {2}} {V_ {m}} $$
$$ m_ {3} = \ frac {V_ {3}} {V_ {m}} $$
$$ m_ {4} = \ frac {V_ {4}} {V_ {m}} $$
위의 회로에는 4 개의 series multiplier resistors, $ R_ {se1}, R_ {se2}, R_ {se3} $ 및 $ R_ {se4} $. 다음은이 네 가지 저항에 해당하는 공식입니다.
$$ R_ {se1} = R_ {m} \ 왼쪽 (m_ {1} -1 \ 오른쪽) $$
$$ R_ {se2} = R_ {m} \ 왼쪽 (m_ {2} -1 \ 오른쪽) $$
$$ R_ {se3} = R_ {m} \ 왼쪽 (m_ {3} -1 \ 오른쪽) $$
$$ R_ {se4} = R_ {m} \ 왼쪽 (m_ {4} -1 \ 오른쪽) $$
따라서 위의 공식을 사용하여 각 직렬 곱셈기 저항의 저항 값을 찾을 수 있습니다.
전기 회로의 두 지점에서 AC 전압을 측정하는 데 사용되는 기기를 AC voltmeter. AC 전압계가 정류기로 구성된 경우 정류기 기반 AC 전압계라고합니다.
DC 전압계는 DC 전압 만 측정합니다. AC 전압을 측정하는 데 사용하려면이 두 단계를 따라야합니다.
Step1 − 정류기를 사용하여 AC 전압 신호를 DC 전압 신호로 변환합니다.
Step2 − 정류기 출력 신호의 DC 또는 평균값을 측정합니다.
우리는 Rectifier based AC voltmeter, 기본 DC 전압계에 정류기 회로를 포함하기 만하면됩니다. 이 장에서는 정류기 기반 AC 전압계에 대해 다룹니다.
정류기 기반 AC 전압계의 유형
다음은 two types 정류기 기반 AC 전압계의.
- 반파 정류기를 사용하는 AC 전압계
- 전파 정류기를 사용하는 AC 전압계
이제이 두 AC 전압계에 대해 하나씩 논의하겠습니다.
반파 정류기를 사용하는 AC 전압계
반파 정류기가 DC 전압계보다 먼저 연결된 경우 전체 조합을 반파 정류기를 사용하는 AC 전압계라고합니다. 그만큼block diagram 반파 정류기를 사용하는 AC 전압계의 그림은 아래 그림과 같습니다.
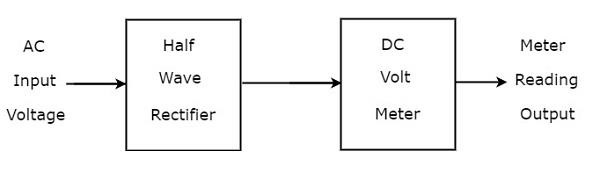
위의 블록 다이어그램은 반파 정류기와 DC 전압계의 두 블록으로 구성됩니다. 위의 블록 다이어그램에서 각 블록을 각 구성 요소로 교체하면 해당 회로 다이어그램을 얻을 수 있습니다. 그래서circuit diagram 반파 정류기를 사용하는 AC 전압계의 경우 아래 그림과 같습니다.
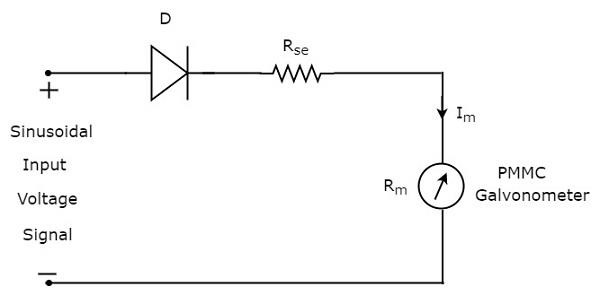
그만큼 rms value 정현파 (AC) 입력 전압 신호의
$$ V_ {rms} = \ frac {V_ {m}} {\ sqrt {2}} $$
$$ \ Rightarrow V_ {m} = \ sqrt {2} V_ {rms} $$
$$ \ Rightarrow V_ {m} = 1.414 V_ {rms} $$
어디,
$ V_ {m} $는 정현파 (AC) 입력 전압 신호의 최대 값입니다.
그만큼 DC 또는 반파 정류기 출력 신호의 평균값은
$$ V_ {dc} = \ frac {V_ {m}} {\ pi} $$
Substitute, 위 방정식에서 $ V_ {m} $의 값.
$$ V_ {dc} = \ frac {1.414 V_ {rms}} {\ pi} $$
$$ V_ {dc} = 0.45V_ {rms} $$
따라서 AC 전압계는 다음과 같은 출력 전압을 생성합니다. 0.45 정현파 (AC) 입력 전압 신호의 rms 값을 곱한 값
전파 정류기를 사용하는 AC 전압계
전파 정류기가 DC 전압계보다 먼저 연결된 경우 전체 조합을 전파 정류기를 사용하는 AC 전압계라고합니다. 그만큼block diagram 전파 정류기를 사용하는 AC 전압계의 그림은 아래 그림과 같습니다.
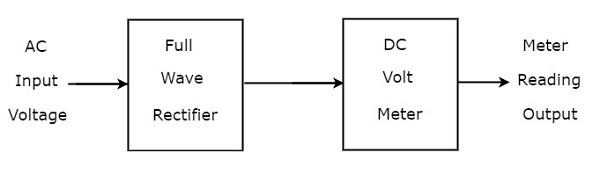
위의 블록 다이어그램은 전파 정류기와 DC 전압계의 두 블록으로 구성됩니다. 위의 블록 다이어그램에서 각 블록을 각 구성 요소로 교체하면 해당 회로 다이어그램을 얻을 수 있습니다.
그래서 circuit diagram 전파 정류기를 사용하는 AC 전압계의 경우는 아래 그림과 같습니다.
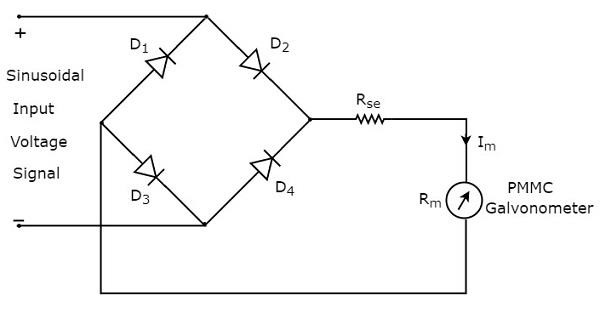
그만큼 rms value 정현파 (AC) 입력 전압 신호의
$$ V_ {rms} = \ frac {V_ {m}} {\ sqrt {2}} $$
$$ \ Rightarrow V_ {m} = \ sqrt {2} \ : V_ {rms} $$
$$ \ 오른쪽 화살표 V_ {m} = 1.414 V_ {rms} $$
어디,
$ V_ {m} $는 정현파 (AC) 입력 전압 신호의 최대 값입니다.
그만큼 DC 또는 전파 정류기 출력 신호의 평균값은
$$ V_ {dc} = \ frac {2V_ {m}} {\ pi} $$
Substitute, 위 방정식에서 $ V_ {m} $의 값
$$ V_ {dc} = \ frac {2 \ times 1.414 \ : V_ {rms}} {\ pi} $$
$$ V_ {dc} = 0.9 \ : V_ {rms} $$
따라서 AC 전압계는 다음과 같은 출력 전압을 생성합니다. 0.9 정현파 (AC) 입력 전압 신호의 rms 값을 곱합니다.
이전 장에서 정류기 기반 AC 전압계에 대해 논의했습니다. 이 장에서는 다음 두 가지 유형의 AC 전압계를 다룹니다.
- 피크 응답 AC 전압계
- AC 전압계에 응답하는 True RMS
이제이 두 가지 유형의 AC 전압계에 대해 하나씩 논의하겠습니다.
피크 응답 AC 전압계
이름에서 알 수 있듯이 피크 응답 AC 전압계는 peak valuesAC 전압 신호의. 즉,이 전압계는 AC 전압의 피크 값을 측정합니다. 그만큼circuit diagram 피크 응답 AC 전압계의 수는 다음과 같습니다.
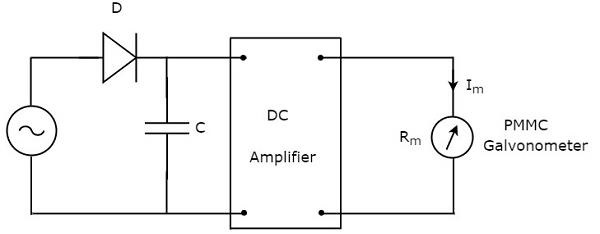
위의 회로는 다이오드, 커패시터, DC 증폭기 및 PMMC 검류계로 구성됩니다. 위의 회로에있는 다이오드는 정류 목적으로 사용됩니다. 따라서 다이오드는 AC 전압 신호를 DC 전압 신호로 변환합니다. 커패시터는이 DC 전압 신호의 피크 값까지 충전됩니다.
동안 positive half cycleAC 전압 신호의 경우 다이오드가 전도되고 커패시터는 AC 전압 신호의 피크 값까지 충전됩니다. AC 전압 신호의 값이이 값보다 작 으면 다이오드가 역 바이어스됩니다.
따라서 커패시터는 AC 전압 신호의 다음 양의 반주기까지 DC 증폭기의 저항을 통해 방전됩니다. AC 전압 신호의 값이 커패시터 전압보다 크면 다이오드가 전도되고 프로세스가 반복됩니다.
커패시터가 빠르게 충전되고 느리게 방전되는 방식으로 구성 요소 값을 선택해야합니다. 결과적으로 미터는 항상이 커패시터 전압에 응답합니다.peak value of AC voltage.
실제 RMS 응답 AC 전압계
이름에서 알 수 있듯이 AC 전압계에 응답하는 실제 RMS는 AC 전압 신호의 실제 RMS 값에 응답합니다. 이 전압계는 AC 전압의 RMS 값을 측정합니다. 그만큼circuit diagram AC 전압계에 응답하는 실제 RMS의 값은 아래 그림과 같습니다.
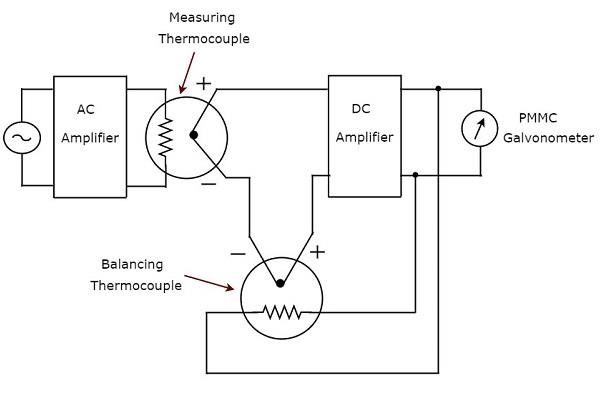
위의 회로는 AC 증폭기, 두 개의 열전대, DC 증폭기 및 PMMC 검류계로 구성됩니다. AC 증폭기는 AC 전압 신호를 증폭합니다. 위의 회로에서 사용되는 두 개의 열전대는 측정 열전대와 균형 열전대입니다.Measuring thermocouple AC 전압 신호의 RMS 값에 비례하는 출력 전압을 생성합니다.
모든 열전대는 입력 수량의 제곱을 일반 수량으로 변환합니다. 이것은 열전대의 출력과 입력 사이에 비선형 관계가 있음을 의미합니다. 열전대의 비선형 동작의 영향은 피드백 회로에서 다른 열전대를 사용하여 무시할 수 있습니다. 위의 회로에서 이러한 목적으로 사용되는 열전대는balancing thermocouple.
두 개의 열전대, 즉 측정 열전대와 균형 열전대는 함께 DC 증폭기의 입력에서 신부를 형성합니다. 결과적으로 미터는 항상true RMS value AC 전압 신호의.
전류는 전하의 흐름 속도입니다. 이 전하가 한 방향으로 만 흐르면 그 결과 전류를 직류 (DC)라고합니다. 직접 전류를 측정하는 데 사용되는 계기는DC ammeter.
PMMC (Permanent Magnet Moving Coil) 검류계와 병렬로 저항을 배치하면 전체 조합이 DC 전류계 역할을합니다. DC 전류계에 사용되는 병렬 저항은 션트 저항이라고도합니다.shunt. 이 저항의 값은 큰 값의 DC 전류를 측정하기 위해 작은 것으로 간주되어야합니다.
그만큼 circuit diagram DC 전류계의 값은 아래 그림과 같습니다.
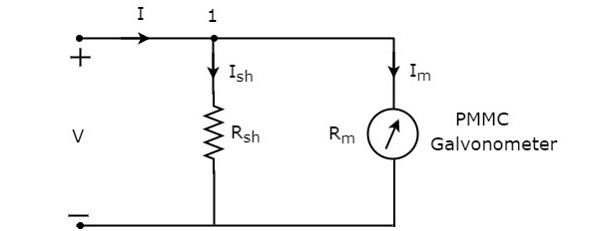
우리는 이것을 배치해야 DC ammeterDC 전류가 측정되는 전기 회로의 분기와 직렬로 연결됩니다. 병렬로 연결된 요소의 전압은 동일합니다. 따라서 션트 저항기 양단 전압 $ R_ {sh} $와 검류계 저항 양단 전압 $ R_ {m} $은이 두 요소가 위의 회로에서 병렬로 연결되어 있기 때문에 동일합니다.Mathematically, 다음과 같이 쓸 수 있습니다.
$$ I_ {sh} R_ {sh} = I_ {m} R_ {m} $$
$ \ Rightarrow R_ {sh} = \ frac {I_ {m} R_ {m}} {I_ {sh}} $ (수식 1)
그만큼 KCL equation 노드 1에서
$$-I + I_ {sh} + I_ {m} = 0 $$
$$ \ 오른쪽 화살표 I_ {sh} = I-I_ {m} $$
Substitute 방정식 1에서 $ I_ {sh} $의 값.
$ R_ {sh} = \ frac {I_ {m} R_ {m}} {I-I_ {m}} $ (방정식 2)
$ I_ {m} $를 분모 항에서 공통적으로 사용하십시오. 이는 방정식 2의 오른쪽에 있습니다.
$$ R_ {sh} = \ frac {I_ {m} R_ {m}} {I_ {m} (\ frac {1} {I_ {m}}-1)} $$
$ \ Rightarrow R_ {sh} = \ frac {R_ {m}} {\ frac {I} {I_ {m}}-1} $ (수식 3)
어디,
$ R_ {sh} $는 션트 저항입니다.
$ R_ {m} $는 검류계의 내부 저항입니다.
$ I $는 측정 할 총 직류입니다.
$ I_ {m} $는 풀 스케일 편향 전류입니다.
측정 할 총 직류의 비율 인 $ I $와 검류계의 풀 스케일 편향 전류 인 $ I_ {m} $는 다음과 같이 알려져 있습니다. multiplying factor, m. 수학적으로 다음과 같이 나타낼 수 있습니다.
$ m = \ frac {I} {I_ {m}} $ (수식 4)
$ R_ {sh} = \ frac {R_ {m}} {m-1} $ (수식 5)
우리는 찾을 수 있습니다 value of shunt resistance 사용 가능한 데이터를 기반으로 방정식 2 또는 방정식 5를 사용합니다.
다중 범위 DC 전류계
이전 섹션에서는 저항을 PMMC 검류계와 병렬로 배치하여 얻은 DC 전류계에 대해 논의했습니다. 이 DC 전류계는particular range 직류의.
DC 전류계를 사용하여 DC 전류를 측정하려면 multiple ranges, 그런 다음 단일 저항 대신 여러 병렬 저항을 사용해야하며이 저항의 전체 조합은 PMMC 검류계와 병렬로 연결됩니다. 그만큼circuit diagram 다중 범위 DC 전류계의 그림은 아래 그림과 같습니다.
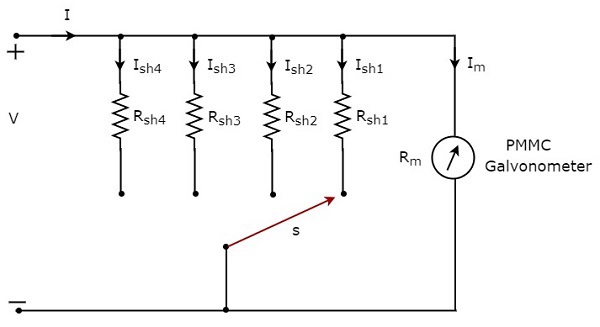
이 다중 범위 DC 전류계를 전기 회로의 분기와 직렬로 배치하여 필요한 범위의 직류 전류를 측정합니다. 원하는 전류 범위는 스위치 s를 각 션트 저항에 연결하여 선택합니다.
$ m_ {1}, m_ {2}, m_ {3} $ 및 $ m_ {4} $는 multiplying factors측정 할 총 직류 전류를 각각 $ I_ {1}, I_ {2}, I_ {3} $ 및 $ I_ {4} $로 고려할 때 DC 전류계의 다음은 각 배율에 해당하는 공식입니다.
$$ m_ {1} = \ frac {I_ {1}} {I_ {m}} $$
$$ m_ {2} = \ frac {I_ {2}} {I_ {m}} $$
$$ m_ {3} = \ frac {I_ {3}} {I_ {m}} $$
$$ m_ {4} = \ frac {I_ {4}} {I_ {m}} $$
위의 회로에는 4 개의 shunt resistors, $ R_ {sh1}, R_ {sh2}, R_ {sh2} $ 및 $ R_ {sh4} $. 다음은이 네 가지 저항에 해당하는 공식입니다.
$$ R_ {sh1} = \ frac {R_ {m}} {m_ {1} -1} $$
$$ R_ {sh2} = \ frac {R_ {m}} {m_ {2} -1} $$
$$ R_ {sh3} = \ frac {R_ {m}} {m_ {3} -1} $$
$$ R_ {sh4} = \ frac {R_ {m}} {m_ {4} -1} $$
위의 공식은 각 션트 저항의 저항 값을 찾는 데 도움이됩니다.
전류는 전하의 흐름 속도입니다. 이 전하의 방향이 정기적으로 바뀌면 결과 전류를Alternating Current (AC).
전기 회로의 모든 분기를 통해 흐르는 교류를 측정하는 데 사용되는 기기를 AC ammeter.
Example − 써모 커플 유형 AC 전류계.
이제 열전쌍 유형 AC 전류계에 대해 논의하겠습니다.
열전대 유형 AC 전류계
PMMC 검류계보다 먼저 써모 커플이 연결된 경우 전체 조합을 써모 커플 유형 AC 전류계라고합니다. 그만큼block diagram 열전대 유형 AC 전류계의 그림은 아래 그림과 같습니다.
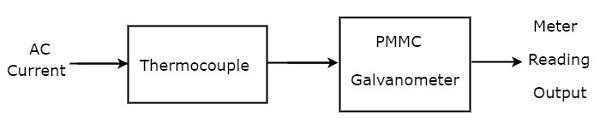
위의 블록 다이어그램은 주로 열전대와 PMMC 검류계의 두 블록으로 구성됩니다. 위의 블록 다이어그램에서 각 블록을 각 구성 요소로 교체하면 해당 회로 다이어그램을 얻을 수 있습니다. 그래서circuit diagram 열전대 유형 AC 전류계의 경우 아래 그림과 같이 표시됩니다.
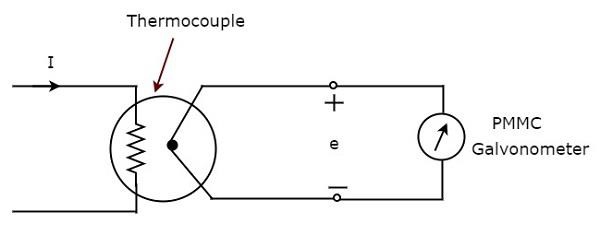
열전대는 교류 I가 히터 소자를 통해 흐를 때마다 EMF, $ e $를 생성합니다. 이 EMF $ e $는 히터 소자를 통해 흐르는 전류 I의 rms 값에 정비례합니다. 따라서 PMMC 기기의 스케일을 보정하여rms values of current.
따라서이 장에서는 DC 전압계, AC 전압계, DC 전류계 및 AC 전류계와 같은 모든 기본 측정 장비를 완성했습니다. 다음 장에서는 저항 값을 측정하는 미터 또는 측정 장비에 대해 논의하겠습니다.
전기 회로의 두 지점 사이의 저항 값을 측정하는 데 사용되는 기기를 ohmmeter. 알 수없는 저항의 값을 찾는데도 사용할 수 있습니다. 저항의 단위는 옴이고 측정기는 미터입니다. 그래서“저항계”라는 단어는“ohm” 과 “meter”.
저항계의 유형
다음은 two types 저항계의.
- 시리즈 저항계
- 션트 저항계
이제이 두 가지 유형의 저항계에 대해 하나씩 논의하겠습니다.
시리즈 저항계
저항기의 값을 알 수없고 저항계와 직렬로 배치하여 측정해야하는 경우 해당 저항계를 직렬 저항계라고합니다. 그만큼circuit diagram 시리즈 저항계는 아래 그림과 같습니다.
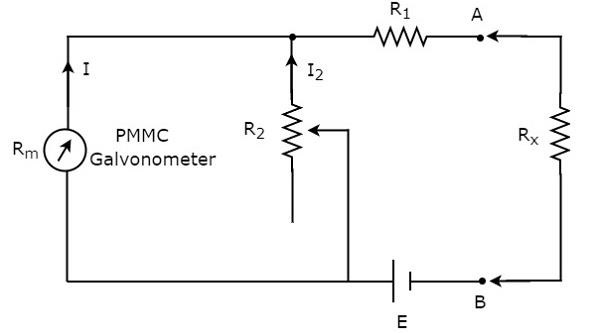
단자 A와 B의 왼쪽에있는 회로 부분은 series ohmmeter. 따라서 알 수없는 저항 값을 단자 A 및 B의 오른쪽에 배치하여 측정 할 수 있습니다. 이제calibration scale 시리즈 저항계의.
$ R_ {x} = 0 \ : \ Omega $이면 단자 A와 B가 서로 단락됩니다. 따라서 미터 전류는 $ R_ {1} $ 및 $ R_ {2} $ 저항으로 나뉩니다. 이제 전체 미터 전류가 저항을 통해 $ R_ {1} $ 만 흐르도록 저항기 $ R_ {2} $ 값을 변경합니다. 이 경우 미터는 전체scale deflection current. 따라서 미터의이 풀 스케일 편향 전류는 $ 0 \ : \ Omega $로 나타낼 수 있습니다.
$ R_ {x} = \ infty \ : \ Omega $이면 터미널 A와 B는 서로 개방 회로가됩니다. 따라서 저항 $ R_ {1} $에는 전류가 흐르지 않습니다. 이 경우 미터는 널 편향 전류를 표시합니다. 따라서 미터의이 널 편향은 $ \ infty \ Omega $로 표시 될 수 있습니다.
이런 식으로 $ R_ {x} $의 다른 값을 고려하여 미터는 다른 처짐을 보여줍니다. 따라서 이에 따라 해당 저항 값으로 이러한 편향을 나타낼 수 있습니다.
시리즈 저항계는 교정 스케일로 구성됩니다. 저울의 오른손과 왼손 끝점에 각각 0 $ \ Omega $ 및 $ \ infty \ : \ Omega $ 표시가 있습니다. 시리즈 저항계는 측정에 유용합니다.high values of resistances.
션트 저항계
저항의 값을 알 수없고 저항계와 병렬 (분로)로 배치하여 측정하려는 경우 해당 저항계를 분로 저항계라고합니다. 그만큼circuit diagram 션트 저항계의 값은 아래 그림에 나와 있습니다.
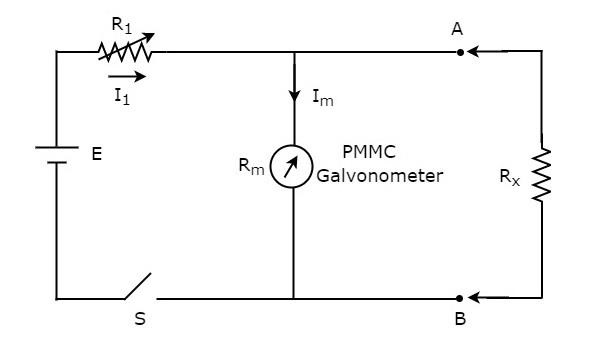
단자 A와 B의 왼쪽에있는 회로 부분은 shunt ohmmeter. 따라서 알 수없는 저항 값을 단자 A와 B의 오른쪽에 배치하여 측정 할 수 있습니다.
이제 calibration scale션트 저항계의. 사용 중에는 위 회로의 스위치 S를 닫으십시오.
$ R_ {x} = 0 \ : \ Omega $이면 터미널 A와 B가 서로 단락됩니다. 이로 인해 전체 전류 $ I_ {1} $가 단자 A 및 B를 통해 흐릅니다.이 경우 PMMC 검류계를 통해 전류가 흐르지 않습니다. 따라서null deflection PMMC 검류계의 값은 $ 0 \ : \ Omega $로 표시 할 수 있습니다.
$ R_ {x} = \ infty \ : \ Omega $이면 터미널 A와 B는 서로 개방 회로가됩니다. 따라서 단자 A와 B를 통해 전류가 흐르지 않습니다.이 경우 전체 전류 $ I_ {1} $가 PMMC 검류계를 통해 흐릅니다. 필요한 경우 PMMC 검류계가 풀 스케일 편향 전류를 표시 할 때까지 저항 값 $ R_ {1} $를 변경 (조정)합니다. 따라서 이것은full scale deflection PMMC 검류계의 전류는 $ \ infty \ : \ Omega $로 나타낼 수 있습니다.
이런 식으로 $ R_ {x} $의 다른 값을 고려하여 미터는 다른 처짐을 보여줍니다. 따라서 이에 따라 해당 저항 값으로 이러한 편향을 나타낼 수 있습니다.
션트 저항계는 교정 스케일로 구성됩니다. 저울의 왼손과 오른손 끝점에 각각 $ 0 \ : \ Omega $ 및 $ \ infty \ : \ Omega $ 표시가 있습니다.
션트 저항계는 측정에 유용합니다. low values of resistances. 따라서 측정 할 저항 값 (예 : 높거나 낮음)에 따라 직렬 저항계 또는 션트 저항계를 사용할 수 있습니다.
이전 장에서 전압계, 전류계 및 저항계에 대해 논의했습니다. 이 측정 장비는 전압, 전류 및 저항을 각각 측정하는 데 사용됩니다. 즉, 우리는separate measuring instruments 전압, 전류 및 저항을 측정합니다.
전압, 전류 및 저항과 같은 양을 한 번에 하나씩 측정하는 데 단일 측정기를 사용할 수 있다고 가정하면 multimeter. 한 번에 하나씩 여러 전기량을 측정 할 수 있기 때문에 멀티 미터라는 이름이 있습니다.
멀티 미터를 사용한 측정
MultimeterDC 및 AC 전압, DC 및 AC 전류 및 여러 범위의 저항을 측정하는 데 사용되는 장비입니다. 전자 멀티 미터 또는 전압 저항계 (VOM)라고도합니다.
DC 전압 측정
의 일부 circuit diagram 아래 그림은 DC 전압 측정에 사용할 수있는 멀티 미터입니다.
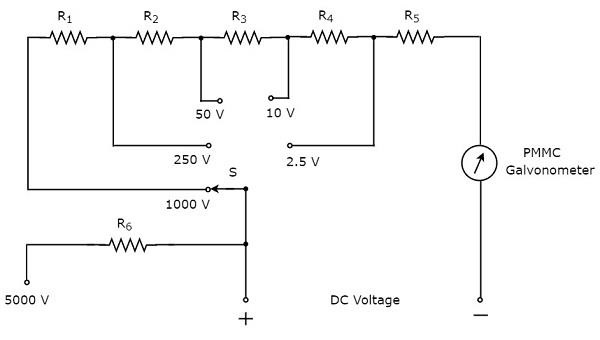
위의 회로는 다중 범위 DC 전압계처럼 보입니다. PMMC 검류계와 직렬로 연결된 저항의 조합은DC voltmeter. 따라서 특정 값까지 DC 전압을 측정하는 데 사용할 수 있습니다.
저항 값을 높여 동일한 DC 전압계로 측정 할 수있는 DC 전압의 범위를 늘릴 수 있습니다. 저항을 연결할 때 등가 저항 값이 증가합니다.series.
위의 회로에서 최대 DC 전압을 측정 할 수 있습니다. 2.5V저항기, $ R_ {5} $를 PMMC 검류계와 직렬로 조합하여 사용합니다. 저항기 $ R_ {4} $를 이전 회로와 직렬로 연결하면 최대 DC 전압을 측정 할 수 있습니다.10V. 이런 식으로 저항을 이전 (이전) 회로와 직렬로 연결하기 만하면 DC 전압 범위를 늘릴 수 있습니다.
스위치 S를 원하는 전압 범위에 연결하여 전기 회로의 두 지점에서 DC 전압을 측정 할 수 있습니다.
DC 전류 측정
의 일부 circuit diagram 아래 그림은 DC 전류 측정에 사용할 수있는 멀티 미터입니다.
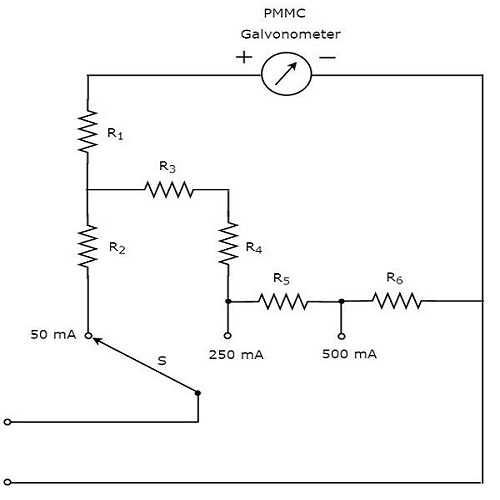
위의 회로는 다중 범위 DC 전류계처럼 보입니다. PMMC 검류계와 병렬로 연결된 저항의 조합은DC ammeter. 따라서 특정 값까지 DC 전류를 측정하는 데 사용할 수 있습니다.
우리는 얻을 수 있습니다 different ranges저항을 이전 저항과 병렬로 배치하여 동일한 DC 전류계로 측정 한 DC 전류의 수. 위의 회로에서 저항 $ R_ {1} $는 대전류로 인해 미터가 손상되는 것을 방지하기 위해 PMMC 검류계와 직렬로 연결됩니다.
스위치 S를 원하는 전류 범위에 연결하여 전기 회로의 두 지점을 통해 흐르는 DC 전류를 측정 할 수 있습니다.
AC 전압 측정
의 일부 circuit diagram AC 전압을 측정하는 데 사용할 수있는 Multimeter의 그림은 아래 그림과 같습니다.

위의 회로는 multi range AC voltmeter. 우리는 정류기를 DC 전압계와 직렬 (캐스케이드)로 배치하는 것만으로 AC 전압계를 얻을 수 있다는 것을 알고 있습니다. 위의 회로는 저항, $ R_ {5} $ 및 PMMC 검류계 사이에 다이오드 조합 및 저항, $ R_ {6} $를 배치하여 생성되었습니다.
스위치 S를 원하는 전압 범위에 연결하여 전기 회로의 두 지점에서 AC 전압을 측정 할 수 있습니다.
저항 측정
의 일부 circuit diagram 저항 측정에 사용할 수있는 Multimeter의 그림은 아래 그림과 같습니다.
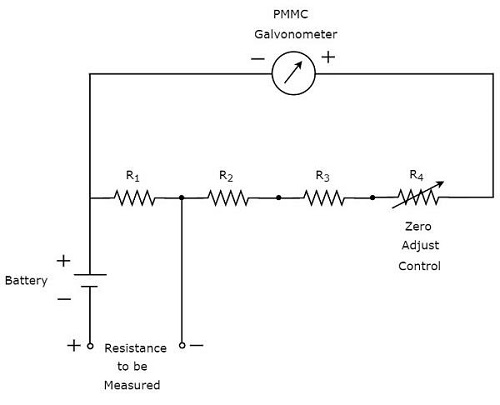
측정을하기 전에 다음 두 가지 작업을 수행해야합니다.
- 기기 단락
- 미터가 최대 전류를 표시 할 때까지 제로 조정 컨트롤을 변경합니다. 즉, 미터는 제로 저항 값을 나타냅니다.
이제 위의 회로는 션트 저항계로 작동하며 스케일 곱셈이 1, 즉 10 0 입니다. 높은 저항을 측정하기위한 배율 곱셈으로 10의 고차 거듭 제곱을 고려할 수도 있습니다.
Signal generator 정현파, 구형파, 삼각파 등과 같은 표준 테스트 신호를 제공하는 전자 장비입니다.주기적인 신호를 생성하기 때문에 발진기라고도합니다.
오디오 주파수 (AF) 범위의 주파수를 갖는 주기적 신호를 생성하는 신호 발생기를 호출합니다. AF signal generator. 오디오 주파수 범위는 20Hz ~ 20KHz입니다.
AF 사인파 및 구형파 생성기
요구 사항에 따라 오디오 주파수 범위에서 사인파 또는 구형파를 생성하는 AF 신호 생성기를 AF 사인 및 구형파 생성기라고합니다. 이것의block diagram아래 그림에 나와 있습니다.
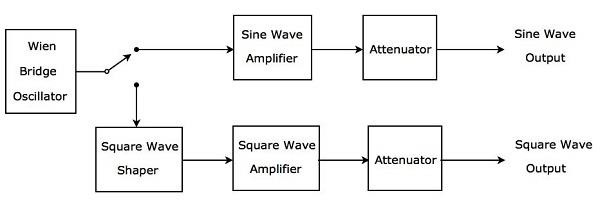
위의 블록 다이어그램은 주로 two paths. 그것들은 위쪽 경로와 아래쪽 경로입니다. 위쪽 경로는 AF 사인파를 생성하는 데 사용되며 아래쪽 경로는 AF 구형파를 생성하는 데 사용됩니다.
Wien bridge oscillator오디오 주파수 범위에서 사인파를 생성합니다. 요구 사항에 따라 Wien 브리지 발진기의 출력을 스위치로 상위 경로 또는 하위 경로에 연결할 수 있습니다.
상단 경로는 사인파 증폭기 및 감쇠기와 같은 블록으로 구성됩니다. 스위치를 사용하여 Wien 브리지 발진기의 출력을 위쪽 경로에 연결하면 원하는AF sine wave 위쪽 경로의 출력에서.
아래쪽 경로는 구형파 셰이퍼, 구형파 증폭기 및 감쇠기의 블록으로 구성됩니다. 구형파 셰이퍼는 사인파를 구형파로 변환합니다. 스위치를 사용하여 Wien 브리지 발진기의 출력을 하위 경로에 연결하면 원하는AF square wave낮은 경로의 출력에서. 이러한 방식으로 우리가 고려한 블록 다이어그램을 사용하여 요구 사항에 따라 AF 사인파 또는 AF 구형파를 생성 할 수 있습니다.
함수 생성기
함수 발생기는 3 개 이상의주기적인 파동을 생성하는 신호 발생기입니다. 다음을 고려하세요block diagram 삼각파, 구형파 및 사인파와 같은주기적인 파동을 생성하는 함수 발생기의.
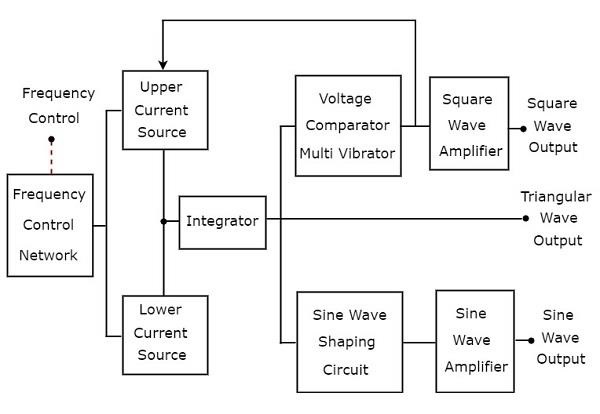
두 가지가있다 current sources즉, 위의 블록 다이어그램에서 상위 전류 소스와 하위 전류 소스입니다. 이 두 전류 소스는 주파수 제어 전압에 의해 조정됩니다.
삼각파
Integrator위의 블록 다이어그램에 나와 있으며 동일한 시간 동안 반복적으로 상부 및 하부 전류 소스에서 정전류를 교대로 얻습니다. 따라서 적분기는 동시에 두 가지 유형의 출력을 반복적으로 생성합니다.
적분기의 출력 전압 increases linearly 적분기가 상위 전류 소스에서 전류를 얻는 기간에 대한 시간과 관련하여.
적분기의 출력 전압 decreases linearly 적분기가 낮은 전류 소스에서 전류를 얻는 기간에 대한 시간과 관련하여.
이런 식으로 위의 블록 다이어그램에있는 적분기는 triangular wave.
구형파 및 사인파
적분기의 출력, 즉 삼각파는 위의 블록 다이어그램과 같이 두 개의 다른 블록에 입력으로 적용되어 각각 구형파와 사인파를 얻습니다. 이 두 가지에 대해 하나씩 논의하겠습니다.
네모 난 파동
삼각파는 동일한 시간 동안 반복적으로 양의 기울기와 음의 기울기를 번갈아가집니다. 그래서voltage comparator multi vibrator 위의 블록 다이어그램에있는 것은 동일한 시간 동안 반복적으로 다음 두 가지 유형의 출력을 생성합니다.
한 가지 유형의 상수 (higher) voltage 전압 비교기 멀티 바이브레이터의 출력에서 전압 비교기 멀티 바이브레이터가 삼각파의 양의 기울기를 얻는 기간 동안.
또 다른 유형의 상수 (lower) voltage 전압 비교기 다중 진동기가 삼각파의 음의 기울기를 얻는 기간 동안 전압 비교기 다중 진동기의 출력에서.
위의 블록 다이어그램에있는 전압 비교기 다중 진동기는 square wave. 전압 비교기 다중 진동기의 출력에서 생성되는 구형파의 진폭이 충분하지 않은 경우 구형파 증폭기를 사용하여 필요한 값으로 증폭 할 수 있습니다.
사인파
그만큼 sine wave shaping circuit삼각 입력 파에서 사인파 출력을 생성합니다. 기본적으로이 회로는 다이오드 저항 네트워크로 구성됩니다. 사인파 형성 회로의 출력에서 생성되는 사인파의 진폭이 충분하지 않은 경우 사인파 증폭기를 사용하여 필요한 값으로 증폭 할 수 있습니다.
파동을 분석하는 데 사용되는 전자 기기를 wave analyzer. 신호와 파동이라는 용어가 자주 혼용 될 수 있기 때문에 신호 분석기라고도합니다.
우리는 periodic signal 다음 두 용어의 합계로.
- DC 구성 요소
- 일련의 정현파 고조파
따라서 주기적 신호의 분석은 그 안에 존재하는 고조파 구성 요소를 분석하는 것입니다.
기본 웨이브 분석기
기본 파동 분석기는 주로 1 차 검출기, 전파 정류기 및 PMMC 검류계의 세 블록으로 구성됩니다. 그만큼block diagram 기본 파 분석기의 그림은 아래 그림과 같습니다.
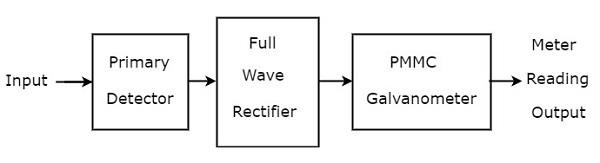
그만큼 function 기본 파형 분석기에 존재하는 각 블록에 대한 설명은 아래와 같습니다.
Primary Detector− LC 회로로 구성되어 있습니다. 측정하고자하는 고조파 주파수 성분 만 허용하는 방식으로 인덕터 L 및 커패시터 C의 값을 조정할 수 있습니다.
Full Wave Rectifier − AC 입력을 DC 출력으로 변환합니다.
PMMC Galvanometer − 전파 정류기의 출력에서 얻은 신호의 피크 값을 보여줍니다.
위의 기본 웨이브 분석기 블록 다이어그램에서 각 블록을 각 구성 요소로 교체하면 해당 회로 다이어그램을 얻을 수 있습니다. 그래서circuit diagram 기본 웨이브 분석기의 그림은 다음과 같습니다.
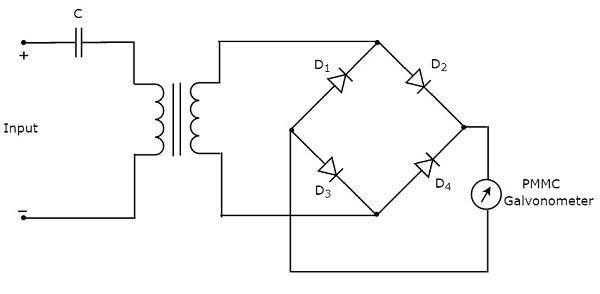
이 기본 웨이브 분석기는 주기적 신호의 모든 고조파 주파수 성분을 분석하는 데 사용할 수 있습니다.
웨이브 분석기의 유형
웨이브 분석기는 다음과 같이 분류 할 수 있습니다. two types.
- 주파수 선택 파 분석기
- 수퍼 헤테로 다 인파 분석기
이제이 두 가지 파동 분석기에 대해 하나씩 논의하겠습니다.
주파수 선택 파 분석기
신호 분석에 사용되는 파동 분석기는 AF 범위에 속합니다. 그만큼block diagram 주파수 선택 파 분석기의 그림은 아래 그림과 같습니다.
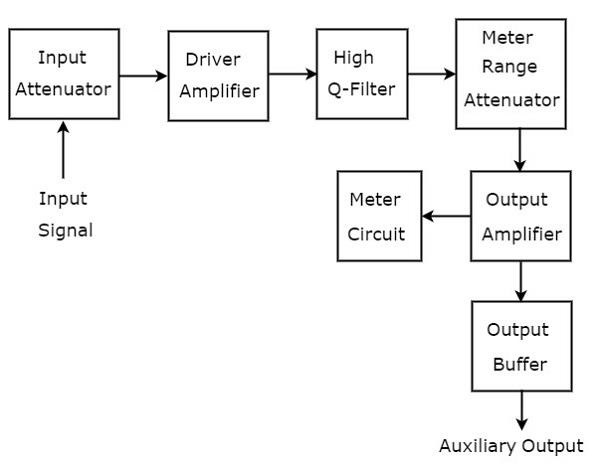
주파수 선택 파 분석기는 블록 세트로 구성됩니다. 그만큼function 각 블록의 아래에 언급되어 있습니다.
Input Attenuator− 분석 할 AF 신호가 입력 감쇠기에 적용됩니다. 신호 진폭이 너무 크면 입력 감쇠기에 의해 감쇠 될 수 있습니다.
Driver Amplifier − 필요할 때마다 수신 된 신호를 증폭합니다.
High Q-filter− 원하는 주파수를 선택하고 원하지 않는 주파수를 거부하는 데 사용됩니다. 두 개의 RC 섹션과 두 개의 필터 증폭기로 구성되며 모두 서로 캐스케이드 연결됩니다. 10의 거듭 제곱으로 주파수 범위를 변경하기 위해 커패시턴스 값을 변경할 수 있습니다. 마찬가지로 선택한 범위 내에서 주파수를 변경하기 위해 저항 값을 변경할 수 있습니다.
Meter Range Attenuator − 선택한 AF 신호를 입력으로 받아 필요할 때마다 감쇠 된 출력을 생성합니다.
Output Amplifier − 필요한 경우 선택한 AF 신호를 증폭합니다.
Output Buffer − 선택한 AF 신호를 출력 장치에 제공하는 데 사용됩니다.
Meter Circuit− 선택한 AF 신호의 판독 값을 표시합니다. 미터 판독 값을 볼트 범위 또는 데시벨 범위로 선택할 수 있습니다.
수퍼 헤테로 다 인파 분석기
RF 범위의 신호를 분석하는 데 사용되는 파동 분석기를 수퍼 헤테로 다인 파동 분석기라고합니다. 다음 그림은block diagram 수퍼 헤테로 다 인파 분석기.
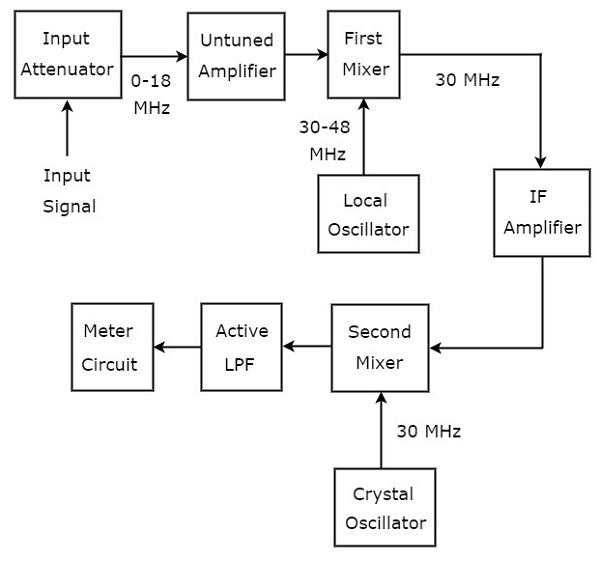
그만큼 working 수퍼 헤테로 다 인파 분석기의 설명은 다음과 같습니다.
분석 할 RF 신호는 입력 감쇠기에 적용됩니다. 신호 진폭이 너무 크면 다음과 같이 감쇠 될 수 있습니다.input attenuator.
Untuned amplifier 필요할 때마다 RF 신호를 증폭하여 첫 번째 믹서에 적용합니다.
RF 신호의 주파수 범위와 로컬 발진기의 출력은 각각 0-18MHz 및 30-48MHz입니다. 그래서,first mixer주파수가 30MHz 인 출력을 생성합니다. 이것이 적용되는 두 신호의 주파수 차이입니다.
IF amplifierIF (Intermediate Frequency) 신호, 즉 첫 번째 믹서의 출력을 증폭합니다. 증폭 된 IF 신호는 두 번째 믹서에 적용됩니다.
증폭 된 IF 신호의 주파수와 수정 발진기의 출력은 30MHz와 동일합니다. 그래서second mixer주파수가 0Hz 인 출력을 생성합니다. 이것이 적용되는 두 신호의 주파수 차이입니다.
차단 주파수 Active Low Pass Filter (LPF)1500Hz로 선택됩니다. 따라서이 필터는 두 번째 믹서의 출력 신호를 허용합니다.
Meter CircuitRF 신호의 판독 값을 표시합니다. 미터 판독 값을 볼트 범위 또는 데시벨 범위로 선택할 수 있습니다.
따라서 분석 할 신호의 주파수 범위를 기반으로 특정 파동 분석기를 선택할 수 있습니다.
주파수 영역에서 파동을 분석하는 데 사용되는 전자 기기를 spectrum analyzer. 기본적으로 CRT 화면에 신호의 에너지 분포를 표시합니다. 여기서 x 축은 주파수를 나타내고 y 축은 진폭을 나타냅니다.
스펙트럼 분석기의 유형
스펙트럼 분석기를 다음과 같이 분류 할 수 있습니다. two types.
- 필터 뱅크 스펙트럼 분석기
- 수퍼 헤테로 다인 스펙트럼 분석기
이제이 두 스펙트럼 분석기에 대해 하나씩 살펴 보겠습니다.
필터 뱅크 스펙트럼 분석기
신호 분석에 사용되는 스펙트럼 분석기는 AF 범위에 속하며 필터 뱅크 스펙트럼 분석기라고합니다. real time spectrum analyzer 모든 입력 주파수의 변동을 표시 (표시)하기 때문입니다.
다음 그림은 block diagram 필터 뱅크 스펙트럼 분석기.
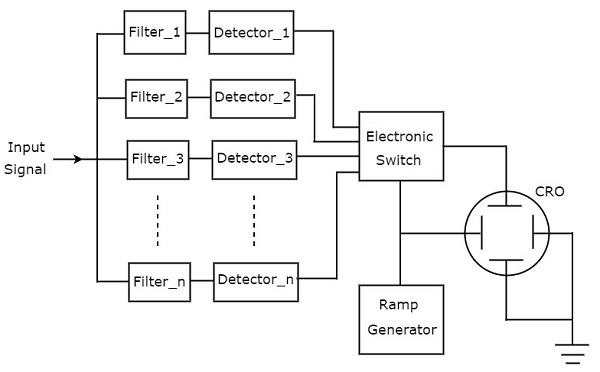
그만큼 working 필터 뱅크 스펙트럼 분석기의 설명은 다음과 같습니다.
대역 통과 필터 세트가 있으며 각 필터는 특정 주파수 대역을 허용하도록 설계되었습니다. 각 대역 통과 필터의 출력은 해당 검출기에 제공됩니다.
모든 감지기 출력은 전자 스위치에 연결됩니다. 이 스위치는 검출기가 CRO의 수직 편향 판에 순차적으로 출력하도록합니다. 그래서 CRO는 주파수를 표시합니다.spectrum of AF signal CRT 화면에서.
수퍼 헤테로 다인 스펙트럼 분석기
신호 분석에 사용되는 스펙트럼 분석기는 RF 범위입니다. superheterodyne spectrum analyzer. 이것의block diagram 아래 그림에 나와 있습니다.
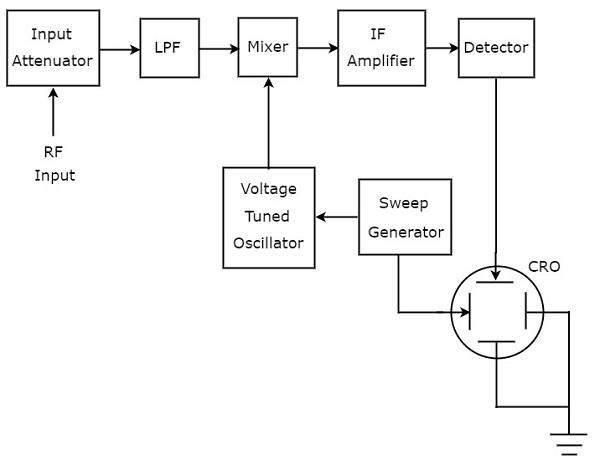
그만큼 working 수퍼 헤테로 다인 스펙트럼 분석기의 설명은 다음과 같습니다.
분석 할 RF 신호는 입력 감쇠기에 적용됩니다. 신호 진폭이 너무 크면 신호 진폭에 의해 감쇠 될 수 있습니다.input attenuator.
Low Pass Filter (LPF)는 차단 주파수보다 작은 주파수 성분 만 허용합니다.
Mixer저역 통과 필터 및 전압 조정 발진기에서 입력을 가져옵니다. 적용되는 두 신호의 주파수 차이 인 출력을 생성합니다.
IF amplifier중간 주파수 (IF) 신호, 즉 믹서의 출력을 증폭합니다. 증폭 된 IF 신호는 검출기에 적용됩니다.
검출기의 출력은 CRO의 수직 편향 판에 제공됩니다. 그래서 CRO는 주파수를 표시합니다.spectrum of RF signal CRT 화면에서.
따라서 분석 할 신호의 주파수 범위를 기반으로 특정 스펙트럼 분석기를 선택할 수 있습니다.
Oscilloscope전압 파형을 표시하는 전자 장비입니다. 오실로스코프 중 CRO (Cathode Ray Oscilloscope)가 기본이며 시변 신호 또는 파형을 표시합니다.
이 장에서는 CRO의 블록 다이어그램과 CRO를 사용한 일부 매개 변수 측정에 대해 설명합니다.
CRO의 블록 다이어그램
음극선 오실로스코프 (CRO)는 블록 세트로 구성됩니다. 수직 증폭기, 지연 라인, 트리거 회로, 타임베이스 생성기, 수평 증폭기, 음극선 관 (CRT) 및 전원 공급 장치입니다. 그만큼block diagram CRO의 수치는 아래 그림과 같습니다.
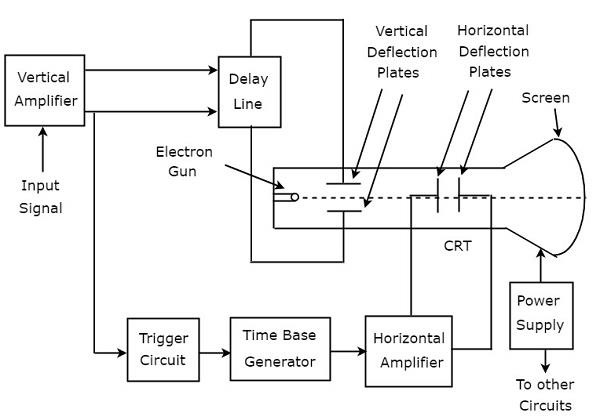
그만큼 function CRO의 각 블록에 대한 설명은 다음과 같습니다.
Vertical Amplifier − CRT 화면에 표시되는 입력 신호를 증폭합니다.
Delay Line− 수직 증폭기의 출력에서 얻은 신호에 일정량의 지연을 제공합니다. 이 지연된 신호는 CRT의 수직 편향 판에 적용됩니다.
Trigger Circuit − 전자빔의 수평 및 수직 편향을 동기화하기 위해 트리거링 신호를 생성합니다.
Time base Generator − 전자빔의 수평 편향에 유용한 톱니 신호를 생성합니다.
Horizontal Amplifier − 톱니파 신호를 증폭 한 다음 CRT의 수평 편향 판에 연결합니다.
Power supply− 높은 전압과 낮은 전압을 모두 생성합니다. 음의 고전압 및 양의 저전압은 각각 CRT 및 기타 회로에 적용됩니다.
Cathode Ray Tube (CRT)− CRO의 주요 중요 블록이며 주로 4 개 부분으로 구성됩니다. 그것들은 전자총, 수직 편향 판, 수평 편향 판 및 형광 스크린입니다.
전자총에 의해 생성 된 전자빔은 각각 한 쌍의 수직 편향 판과 한 쌍의 수평 편향 판에 의해 수직 및 수평 방향으로 편향됩니다. 마지막으로, 편향된 빔이 형광 스크린에 스폿으로 나타납니다.
이런 식으로 CRO는 적용된 입력 신호를 CRT 화면에 표시합니다. 따라서 CRO를 사용하여 시간 영역에서 신호를 분석 할 수 있습니다.
CRO를 사용한 측정
CRO를 사용하여 다음 측정을 수행 할 수 있습니다.
- 진폭 측정
- 기간 측정
- 주파수 측정
이제 이러한 측정에 대해 하나씩 논의하겠습니다.
진폭 측정
CRO는 화면에 시간 함수로 전압 신호를 표시합니다. 그만큼amplitude 전압 신호의 비율은 일정하지만 전압 신호를 덮는 분할 수를 수직 방향으로 volt/divisionCRO 패널의 노브. 따라서 우리는amplitude 다음 공식을 사용하여 CRO 화면에 나타나는 신호의.
$$ A = j \ times n_ {v} $$
어디,
$ A $는 진폭입니다.
$ j $는 볼트 / 디비전의 값입니다.
$ n_ {v} $는 수직 방향으로 신호를 덮는 분할 수입니다.
기간 측정
CRO는 화면에 시간 함수로 전압 신호를 표시합니다. 그만큼Time period 주기적인 전압 신호의 비율은 일정하지만 수평 방향으로 하나의 완전한 전압 신호 사이클을 커버하는 분할 수를 변경할 수 있습니다. time/division CRO 패널의 노브.
따라서 우리는 Time period 다음 공식을 사용하여 CRO 화면에 나타나는 신호의.
$$ T = k \ times n_ {h} $$
어디,
$ T $는 기간입니다.
$ j $는 시간 / 분할 값입니다.
$ n_ {v} $는 수평 방향으로주기 신호의 하나의 완전한 사이클을 커버하는 분할 수입니다.
주파수 측정
주기적 신호의 주파수 f는 기간 T의 역수입니다. Mathematically, 다음과 같이 나타낼 수 있습니다.
$$ f = \ frac {1} {T} $$
따라서 우리는이 두 단계를 따라 주기적 신호의 주파수 f를 찾을 수 있습니다.
Step1 − 찾기 Time period 주기적 신호
Step2 − 테이크 reciprocal Step1에서 얻은 주기적 신호의 시간주기
다음 장에서 특수 목적 오실로스코프에 대해 설명합니다.
이전 장에서는 기본 오실로스코프 인 CRO (Cathode Ray Oscilloscope)에 대해 논의했습니다. 요구 사항에 따라 기본 오실로스코프에 추가 블록을 거의 포함하지 않는 것만으로 특수 목적 오실로스코프를 얻을 수 있습니다.
다음은 special purpose oscilloscopes.
- 듀얼 빔 오실로스코프
- 듀얼 트레이스 오실로스코프
- 디지털 스토리지 오실로스코프
이제 이러한 특수 목적 오실로스코프에 대해 하나씩 살펴 보겠습니다.
듀얼 빔 오실로스코프
두 개의 전압 파형을 표시하는 오실로스코프를 듀얼 빔 오실로스코프라고합니다. 이것의block diagram 아래 그림에 나와 있습니다.
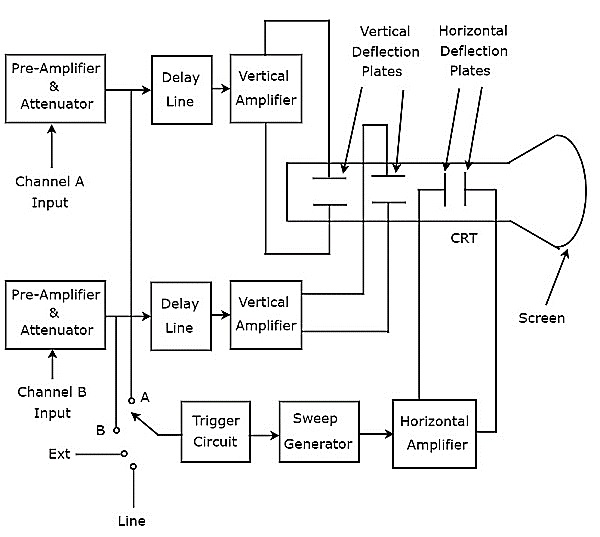
위 그림과 같이 듀얼 빔 오실로스코프의 CRT는 두 세트의 수직 편향 플레이트와 한 세트의 수평 편향 플레이트로 구성됩니다.
다음 블록의 조합을 channel.
- 프리 앰프 및 감쇠기
- 지연 라인
- 수직 증폭기
- 수직 편향 판 세트
듀얼 빔 오실로스코프에는 두 개의 채널이 있습니다. 따라서 A와 B라는 두 신호를 각각 채널 A와 채널 B의 입력으로 적용 할 수 있습니다. 이 네 가지 신호 중 하나를 다음과 같이 선택할 수 있습니다.trigger input스위치를 사용하여 트리거 회로에 연결합니다. 입력 신호 A 및 B, 외부 신호 (Ext) 및 라인 입력입니다.
이 오실로스코프는 두 쌍의 수직 편향 플레이트가 있기 때문에 두 개의 수직 편향 빔을 생성합니다. 이 오실로스코프에서 빔을 수평 방향으로 편향시키는 데 유용한 블록은 두 입력 신호 모두에 공통입니다. 마지막으로이 오실로스코프는two input signals CRT 화면에서 동시에.
듀얼 트레이스 오실로스코프
화면에 두 개의 트레이스를 생성하는 오실로스코프를 듀얼 트레이스 오실로스코프라고합니다. 이것의block diagram 아래 그림에 나와 있습니다.
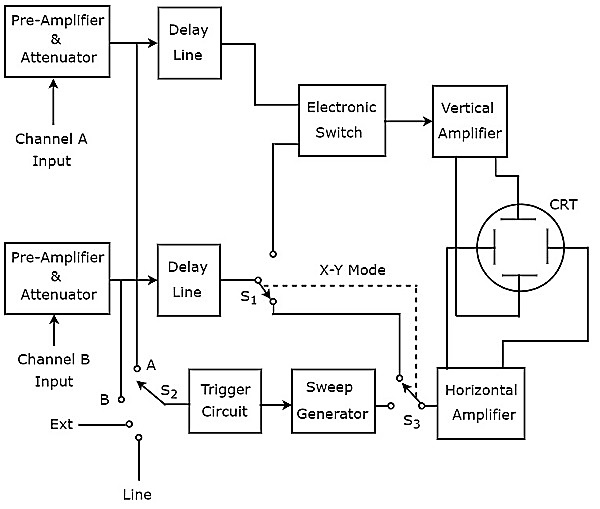
위 그림에서 볼 수 있듯이 듀얼 트레이스 오실로스코프의 CRT는 수직 편향 플레이트 세트와 또 다른 수평 편향 플레이트 세트로 구성됩니다. 채널은 4 개의 블록, 즉 프리 앰프 및 감쇠기, 지연 라인, 수직 증폭기 및 수직 편향 판으로 구성됩니다.
위의 블록 다이어그램에서 처음 두 블록은 두 채널에 별도로 존재합니다. 마지막 두 블록은 두 채널에 공통입니다. 따라서, 도움으로electronic switch 특정 채널의 지연 선 출력을 수직 증폭기에 연결할 수 있습니다.
이 네 가지 신호 중 하나를 트리거 입력으로 선택할 수 있습니다. trigger circuit스위치를 사용하여. 입력 신호 A 및 B, 외부 신호 (Ext) 및 라인 입력입니다.
이 오실로스코프는 전자 스위치를 사용하여 입력 신호 A 및 B를 수직 방향으로 편향시키기 위해 동일한 전자 빔을 사용하고 two traces. 빔을 수평으로 편향시키는 블록은 두 입력 신호 모두에 공통입니다.
디지털 스토리지 오실로스코프
파형을 디지털로 저장하는 오실로스코프를 디지털 스토리지 오실로스코프라고합니다. 그만큼block diagram (디지털) 스토리지 오실로스코프의
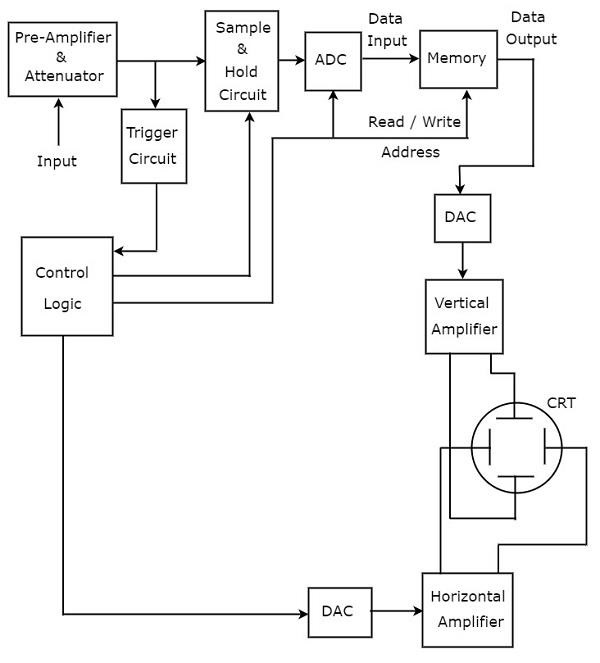
디지털 데이터 저장에 필요한 추가 블록이 기본 오실로스코프에 추가되어 디지털 저장 오실로스코프로 변환됩니다. 필요한 블록storing of digital data디지털 스토리지 오실로스코프의 전치 증폭기 및 감쇠기와 수직 증폭기 사이에 있습니다. 샘플 앤 홀드 회로, 아날로그-디지털 변환기 (ADC), 메모리 및 디지털-아날로그 변환기입니다.
Control logic다양한 제어 신호를 전송하여 처음 세 블록을 제어합니다. 제어 로직 및 디지털-아날로그 변환기와 같은 블록은 디지털 스토리지 오실로스코프의 트리거 회로와 수평 증폭기 사이에 있습니다.
디지털 스토리지 오실로스코프 stores the data화면에 파형을 표시하기 전에 디지털로. 반면 기본 오실로스코프에는이 기능이 없습니다.
Lissajous figureCRO의 수평 및 수직 편향 판 모두에 사인파 신호가 적용될 때 화면에 표시되는 패턴입니다. 이러한 패턴은 CRO의 수평 및 수직 편향 플레이트 모두에 적용되는 정현파 신호의 진폭, 주파수 및 위상차에 따라 달라집니다.
다음 그림은 example Lissajous 그림의.
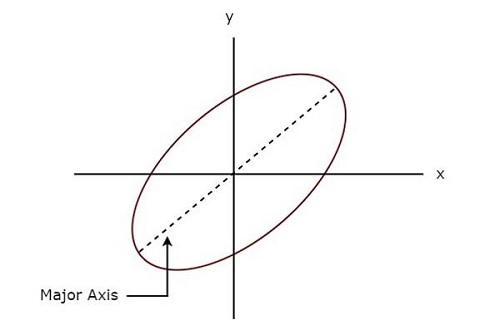
위의 Lissajous 그림은 elliptical shape 장축은 양의 x 축과 약간의 경사각을 가지고 있습니다.
Lissajous Figure를 사용한 측정
우리는 다음을 할 수 있습니다 two measurements Lissajous 그림에서.
- 정현파 신호의 주파수
- 두 정현파 신호 간의 위상차
이제이 두 측정에 대해 하나씩 논의 해 보겠습니다.
주파수 측정
CRO의 수평 및 수직 편향 판 모두에 사인파 신호가 적용되면 Lissajous 그림이 화면에 표시됩니다. 따라서 표준이있는 정현파 신호를 적용합니다.known frequencyCRO의 수평 편향 판에. 마찬가지로 사인파 신호를 적용합니다.frequency 이다 unknown CRO의 수직 편향 판에
$ f_ {H} $ 및 $ f_ {V} $는 CRO의 수평 및 수직 편향 판에 각각 적용되는 사인파 신호의 주파수입니다. $ f_ {H} $와 $ f_ {V} $의 관계는 다음과 같습니다.mathematically 아래와 같이 표현됩니다.
$$ \ frac {f_ {V}} {f_ {H}} = \ frac {n_ {H}} {n_ {V}} $$
위의 관계에서 우리는 CRO의 수직 편향 판에 적용되는 정현파 신호의 주파수를 얻을 수 있습니다.
$ f_ {V} = \ left (\ frac {n_ {H}} {n_ {V}} \ right) f_ {H} $ (수식 1)
어디,
$ n_ {H} $는 수평 접선의 수입니다.
$ n_ {V} $는 수직 접선의 수입니다.
Lissajous 그림에서 $ n_ {H} $ 및 $ n_ {V} $의 값을 찾을 수 있습니다. 따라서 방정식 1에서 $ n_ {H} $, $ n_ {V} $ 및 $ f_ {H} $의 값을 대체하여 다음 값을 얻습니다.$f_{V}$, 즉 frequency of sinusoidal signal CRO의 수직 편향 판에 적용됩니다.
위상차 측정
CRO의 수평 및 수직 편향 판 모두에 사인파 신호가 적용되면 Lissajous 그림이 화면에 표시됩니다. 따라서 정현파 신호를 적용하십시오.same amplitude and frequency CRO의 수평 및 수직 편향 판 모두에.
모양을 기반으로 한 일부 Lissajous 그림의 경우 두 정현파 신호 간의 위상 차이를 직접 알 수 있습니다.
Lissajous 그림이 straight line 양의 x 축에 $ 45 ^ {\ circ} $ 경사면 phase difference두 정현파 신호 사이는 $ 0 ^ {\ circ} $가됩니다. 즉, 두 정현파 신호간에 위상차가 없습니다.
Lissajous 그림이 straight line 양의 x 축에 $ 135 ^ {\ circ} $ 경사면 phase difference두 정현파 신호 사이에는 $ 180 ^ {\ circ} $가됩니다. 즉,이 두 정현파 신호는 위상이 맞지 않습니다.
Lissajous 그림이 circular shape, 그러면 두 정현파 신호 간의 위상차는 $ 90 ^ {\ circ} $ 또는 $ 270 ^ {\ circ} $가됩니다.
Lissajous 수치가 다음과 같을 때 공식을 사용하여 두 정현파 신호 간의 위상차를 계산할 수 있습니다. elliptical shape.
경사각이있는 타원형 Lissajous 도형의 장축이 양의 x 축으로 $ 0 ^ {\ circ} $와 $ 90 ^ {\ circ} $ 사이에 있으면 두 정현파 신호의 위상차가됩니다.
$$ \ phi = \ sin ^ {-1} \ left (\ frac {x_ {1}} {x_ {2}} \ right) = \ sin ^ {-1} \ left (\ frac {y_ {1} } {y_ {2}} \ 오른쪽) $$
경사각이있는 타원형 Lissajous 도형의 장축이 양의 x 축으로 $ 90 ^ {\ circ} $에서 $ 180 ^ {\ circ} $ 사이에 있으면 두 정현파 신호의 위상차가됩니다.
$$ \ phi = 180-\ sin ^ {-1} \ left (\ frac {x_ {1}} {x_ {2}} \ right) = 180-\ sin ^ {-1} \ left (\ frac { y_ {1}} {y_ {2}} \ 오른쪽) $$
Where,
$ x_ {1} $는 원점에서 x 축 점까지의 거리이며, 여기서 타원형 Lissajous 그림이 교차합니다.
$ x_ {2} $는 원점에서 타원형 Lissajous 그림의 수직 접선까지의 거리입니다.
$ y_ {1} $는 원점에서 Y 축의 점까지의 거리이며, 여기서 타원형 Lissajous 그림이 교차합니다.
$ y_ {2} $는 원점에서 타원형 Lissajous 그림의 수평 접선까지의 거리입니다.
이 장에서는 공식을 사용하여 Lissajous 그림에서 두 개의 정현파 신호 간의 미지 정현파 신호의 주파수와 위상차를 찾는 방법을 배웠습니다.
프로브를 통해 모든 테스트 회로를 오실로스코프에 연결할 수 있습니다. CRO는 기본 오실로스코프이므로 이에 연결된 프로브를CRO probe.
테스트 회로에 부하 문제를 일으키지 않는 방식으로 프로브를 선택해야합니다. 그래서 CRO 화면에서 신호로 테스트 회로를 제대로 분석 할 수 있습니다.
CRO 프로브에는 다음이 있어야합니다. characteristics.
- 높은 임피던스
- 높은 대역폭
그만큼 block diagram CRO 프로브의 구성은 아래 그림과 같습니다.
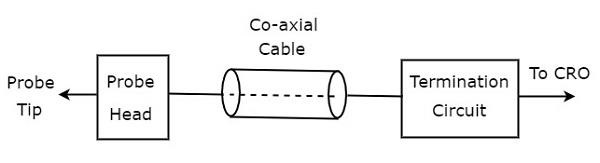
그림과 같이 CRO 프로브는 주로 세 개의 블록으로 구성됩니다. 그것들은 프로브 헤드, 동축 케이블 및 종단 회로입니다. 동축 케이블은 프로브 헤드와 종단 회로를 간단히 연결합니다.
CRO 프로브의 유형
CRO 프로브는 다음과 같이 분류 할 수 있습니다. two types.
- 패시브 프로브
- 액티브 프로브
이제이 두 가지 유형의 프로브에 대해 하나씩 살펴 보겠습니다.
패시브 프로브
프로브 헤드가 수동 요소로 구성된 경우 passive probe. 패시브 프로브의 회로도는 아래 그림과 같습니다.
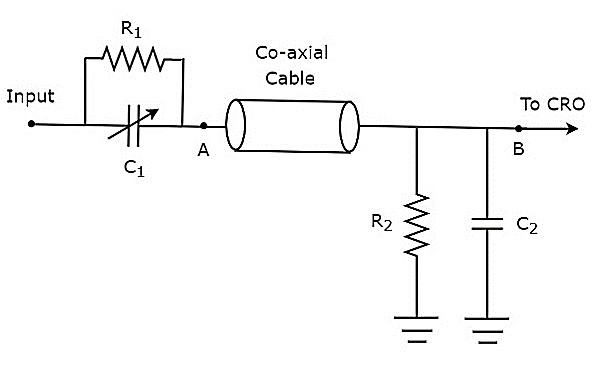
그림과 같이 프로브 헤드는 저항 $ R_ {1} $와 가변 커패시터 $ C_ {1} $의 병렬 조합으로 구성됩니다. 마찬가지로 종단 회로는 저항 $ R_ {2} $와 커패시터 $ C_ {2} $의 병렬 조합으로 구성됩니다.
위의 회로도는 다음과 같은 형태로 수정됩니다. bridge circuit 아래 그림과 같습니다.
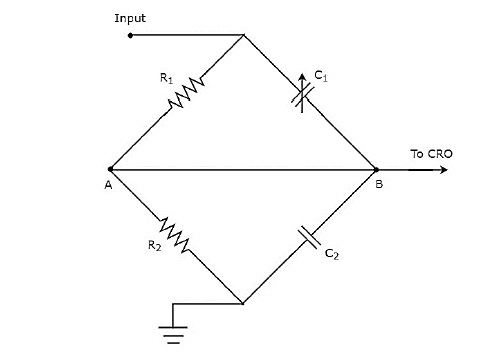
가변 커패시터 $ c_ {1} $의 값을 조정하여 브리지의 균형을 맞출 수 있습니다. 다음 장에서 브리지의 개념에 대해 설명합니다. 당분간 다음을 고려하십시오.balancing condition of AC bridge.
$$ Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $$
Substitute, 임피던스 $ Z_ {1}, Z_ {2}, Z_ {3} $ 및 $ Z_ {4} $ ($ R_ {1}, \ frac {1} {j \ omega C_ {1}}, R_ {) 위 방정식에서 각각 2} $ 및 $ \ frac {1} {j \ omega C_ {2}} $.
$$ R_ {1} \ left (\ frac {1} {j \ omega C_ {2}} \ right) = \ left (\ frac {1} {j \ omega C_ {1}} \ right) R_ {2 } $$
$ \ Rightarrow R_ {1} C_ {1} = R_ {2} C_ {2} $ 방정식 1
전압 분할 원리에 따라 우리는 voltage across resistor, $R_{2}$ 같이
$$ V_ {0} = V_ {i} \ 왼쪽 (\ frac {R_ {2}} {R_ {1} + R_ {2}} \ 오른쪽) $$
attenuation factor입력 전압 $ V_ {i} $와 출력 전압 $ V_ {0} $의 비율입니다. 따라서 위의 방정식에서 감쇠 계수 $ \ alpha $를 얻을 수 있습니다.
$$ \ alpha = \ frac {V_ {i}} {V_ {0}} = \ frac {R_ {1} + R_ {2}} {R_ {2}} $$
$ \ Rightarrow \ alpha = 1+ \ frac {R_ {1}} {R_ {2}} $
$ \ Rightarrow \ alpha-1 = \ frac {R_ {1}} {R_ {2}} $
$ \ Rightarrow R_ {1} = \ left (\ alpha-1 \ right) R_ {2} $ 방정식 2
방정식 2에서 $ R_ {1} $의 값이 $ \ : \ alpha> 1 $의 정수 값에 대해 ð ?? '… 2의 값보다 크거나 같다는 결론을 내릴 수 있습니다.
방정식 1에서 방정식 2를 대체합니다.
$$ \ 왼쪽 (\ alpha-1 \ 오른쪽) R_ {2} C_ {1} = R_ {2} C_ {2} $$
$ \ Rightarrow \ left (\ alpha-1 \ right) C_ {1} = C_ {2} $
$ \ Rightarrow C_ {1} = \ frac {C_ {2}} {\ left (\ alpha-1 \ right)} $ 방정식 3
방정식 3에서 $ C_ {1} $의 값이 $ \ alpha> 1 $의 정수 값에 대해 $ C_ {2} $의 값보다 작거나 같다는 결론을 내릴 수 있습니다.
Example
감쇠 계수 $ \ alpha $가 10 인 프로브의 $ R_ {1} $ 및 $ C_ {1} $ 값을 찾아 보겠습니다. $ R_ {2} = 1 M \ Omega $ 및 $ C_ {2} = 18pF $.
Step1 − 수식 2에서 $ \ alpha $ 및 $ R_ {2} $ 값을 대체하여 $ R_ {1} $ 값을 얻습니다.
$$ R_ {1} = \ 왼쪽 (10-1 \ 오른쪽) \ times 1 \ times 10 ^ {6} $$
$$ \ Rightarrow R_ {1} = 9 \ times 10 ^ {6} $$
$$ \ Rightarrow R_ {1} = 9M \ Omega $$
Step 2 − 수식 3에서 $ \ alpha $ 및 $ C_ {2} $ 값을 대체하여 $ C_ {1} $ 값을 얻습니다.
$$ C_ {1} = \ frac {18 \ times10 ^ {-12}} {\ left (10-1 \ right)} $$
$$ \ Rightarrow C_ {1} = 2 \ times 10 ^ {-12} $$
$$ \ Rightarrow C_ {1} = 2 pF $$
따라서 프로브의 $ R_ {1} $ 및 $ C_ {1} $ 값은 주어진 사양에 대해 각각 $ 9M \ Omega $ 및 $ 2pF $가됩니다.
액티브 프로브
프로브 헤드가 활성 전자 부품으로 구성된 경우 active probe. 활성 프로브의 블록 다이어그램은 아래 그림과 같습니다.

그림에 표시된 것처럼 프로브 헤드는 BJT 이미 터 팔로워가있는 캐스케이드의 FET 소스 팔로워로 구성됩니다. FET 소스 팔로워는 높은 입력 임피던스와 낮은 출력 임피던스를 제공합니다. 반면 BJT 이미 터 팔로워의 목적은 임피던스 불일치를 방지하거나 제거하는 것입니다.
동축 케이블 및 종단 회로와 같은 다른 두 부분은 액티브 및 패시브 프로브 모두에서 동일하게 유지됩니다.
전기 구성 요소가 브리지 또는 링 구조의 형태로 배열 된 경우 해당 전기 회로를 bridge. 일반적으로 브리지는 4 개의 팔 또는 가지 세트로 루프를 형성합니다. 각 분기에는 하나 또는 두 개의 전기 구성 요소가 포함될 수 있습니다.
교량의 종류
브리지 회로 또는 브리지를 작동 할 수있는 전압 신호에 따라 다음 두 가지 범주로 분류 할 수 있습니다.
- DC 브리지
- AC 브리지
이제이 두 다리에 대해 간략하게 논의하겠습니다.
DC 브리지
브리지 회로가 DC 전압 신호로만 작동 할 수 있다면 DC 브리지 회로이거나 단순히 DC bridge. DC 브리지는 알 수없는 저항 값을 측정하는 데 사용됩니다. 그만큼circuit diagram DC 브리지의 모양은 아래 그림과 같습니다.
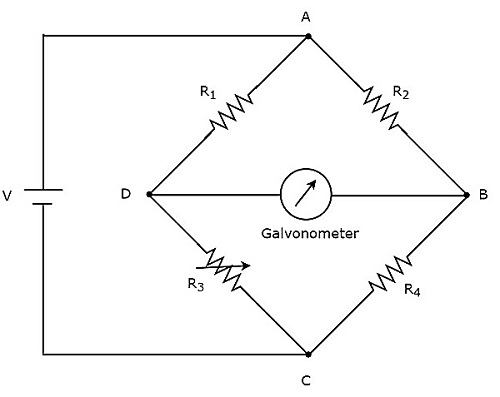
위의 DC 브리지에는 four arms각 암은 저항으로 구성됩니다. 이 중 두 개의 저항은 고정 된 저항 값을 가지며, 하나는 가변 저항이고 다른 하나는 알 수없는 저항 값을 가지고 있습니다.
위의 DC 브리지 회로는 DC voltage source하나의 대각선에 배치합니다. 검류계는 DC 브리지의 다른 대각선에 배치됩니다. 다리의 균형이 맞지 않는 한 약간의 처짐을 보여줍니다.
검류계가 영 (0) 편향을 나타낼 때까지 가변 저항의 저항 값을 변경합니다. 이제 위의 DC 브리지는 균형 잡힌 브리지라고합니다. 따라서 우리는unknown resistance 절점 방정식을 사용하여.
AC 브리지
브리지 회로가 AC 전압 신호만으로 작동 할 수있는 경우 AC 브리지 회로 또는 간단히 AC bridge. AC 브리지는 알 수없는 인덕턴스, 커패시턴스 및 주파수 값을 측정하는 데 사용됩니다.
그만큼 circuit diagram AC 브리지의 모양은 아래 그림과 같습니다.

AC 브리지의 회로도는 DC 브리지의 회로도와 유사합니다. 위의 AC 브리지에는four arms각 암은 임피던스로 구성됩니다. 즉, 각 암은 저항, 인덕터 및 커패시터와 같은 수동 요소의 단일 또는 조합을 갖게됩니다.
4 개의 임피던스 중 2 개의 임피던스는 고정 된 값을 가지며, 하나는 가변적이고 다른 하나는 알 수없는 임피던스입니다.
위의 AC 브리지 회로는 AC voltage source하나의 대각선에 배치합니다. 감지기는 AC 브리지의 다른 대각선에 배치됩니다. 다리가 균형이 맞지 않는 한 약간의 처짐을 보여줍니다.
위의 AC 브리지 회로는 AC voltage source하나의 대각선에 배치합니다. 감지기는 AC 브리지의 다른 대각선에 배치됩니다. 다리가 균형이 맞지 않는 한 약간의 처짐을 보여줍니다.
감지기가 널 (제로) 편향을 보일 때까지 가변 임피던스의 임피던스 값을 변경하십시오. 이제 위의 AC 브리지는 균형 잡힌 브리지라고합니다. 따라서 우리는unknown impedance 균형 잡힌 조건을 사용하여.
DC bridgesDC 전압 신호로만 작동 할 수 있습니다. DC 브리지는 브리지에 존재하는 알 수없는 저항 값을 측정하는 데 유용합니다. 휘트 스톤 브리지는 DC 브리지의 한 예입니다.
이제 논의 해 보겠습니다. Wheatstone’s Bridge 알려지지 않은 저항의 값을 찾기 위해.
휘트 스톤의 다리
휘트 스톤의 다리는 주로 팔이 4 개인 단순한 DC 다리입니다. 이 4 개의 암은 마름모 또는 정사각형 모양을 형성하고 각 암은 하나의 저항으로 구성됩니다.
알 수없는 저항 값을 찾으려면 검류계와 DC 전압 소스가 필요합니다. 따라서이 두 개 중 하나는 Wheatstone 다리의 한 대각선에 배치되고 다른 하나는 Wheatstone 다리의 다른 대각선에 배치됩니다.
휘트 스톤 브리지는 중간 저항 값을 측정하는 데 사용됩니다. 그만큼circuit diagram 휘트 스톤 다리의 모습은 아래 그림과 같습니다.
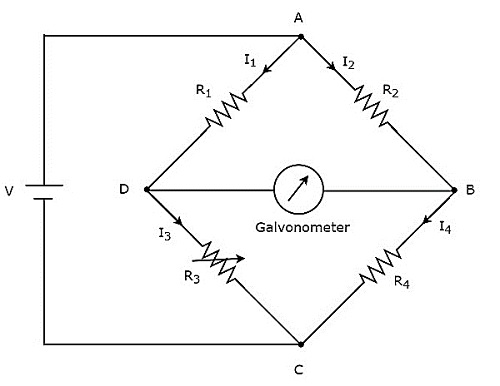
위의 회로에서 암 AB, BC, CD 및 DA는 함께 rhombus또는 사각형 모양. 저항기는 각각 $ R_ {2} $, $ R_ {4} $, $ R_ {3} $ 및 $ R_ {1} $로 구성됩니다. 이 저항기 암을 통해 흐르는 전류를 각각 $ I_ {2} $, $ I_ {4} $, $ I_ {3} $ 및 $ I_ {1} $로하고 이러한 전류의 방향이 그림에 나와 있습니다.
대각선 암 DB 및 AC는 각각 V 볼트의 검류계와 DC 전압 소스로 구성됩니다. 여기서 저항 $ R_ {3} $는 표준 가변 저항이고 저항 $ R_ {4} $는 알 수없는 저항입니다. 우리는 할 수 있습니다balance the bridge, 저항기의 저항 값 $ R_ {3} $를 변경하여.
위의 브리지 회로는 대각선 암 DB를 통해 전류가 흐르지 않을 때 균형을 이룹니다. 즉,no deflection 검류계에서 브리지가 균형을 이룰 때.
다음과 같은 경우 브리지가 균형을 이룹니다. two conditions 만족합니다.
암 AD의 전압은 암 AB의 전압과 같습니다. 즉,
$$ V_ {AD} = V_ {AB} $$
$ \ Rightarrow I_ {1} R_ {1} = I_ {2} R_ {2} $ 방정식 1
암 DC의 전압은 암 BC의 전압과 같습니다. 즉,
$$ V_ {DC} = V_ {BC} $$
$ \ Rightarrow I_ {3} R_ {3} = I_ {4} R_ {4} $ 방정식 2
위의 두 가지 균형 조건에서 다음을 얻습니다. two conclusions.
암 AD를 통해 흐르는 전류는 암 DC의 전류와 동일합니다. 즉,
$$ I_ {1} = I_ {3} $$
암 AB를 통해 흐르는 전류는 암 BC의 전류와 같습니다. 즉,
$$ I_ {2} = I_ {4} $$
방정식 1과 방정식 2의 비율을 취하십시오.
$ \ frac {I_ {1} R_ {1}} {I_ {3} R_ {3}} = \ frac {I_ {2} R_ {2}} {I_ {4} R_ {4}} $ 방정식 3
방정식 3에서 $ I_ {1} = I_ {3} $ 및 $ I_ {2} = I_ {4} $를 대체합니다.
$$ \ frac {I_ {3} R_ {1}} {I_ {3} R_ {3}} = \ frac {I_ {4} R_ {2}} {I_ {4} R_ {4}} $$
$$ \ Rightarrow \ frac {R_ {1}} {R_ {3}} = \ frac {R_ {2}} {R_ {4}} $$
$$ \ Rightarrow R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $$
위 방정식에서 알려진 저항기 $ R_ {1} $, $ R_ {2} $ 및 $ R_ {3} $ 값을 대입하면 value of resistor,$R_{4}$.
이 장에서는 인덕턴스를 측정하는 데 사용할 수있는 AC 브리지에 대해 설명합니다. AC 브리지는 AC 전압 신호로만 작동합니다. 그만큼circuit diagram AC 브리지의 구성은 아래 그림과 같습니다.
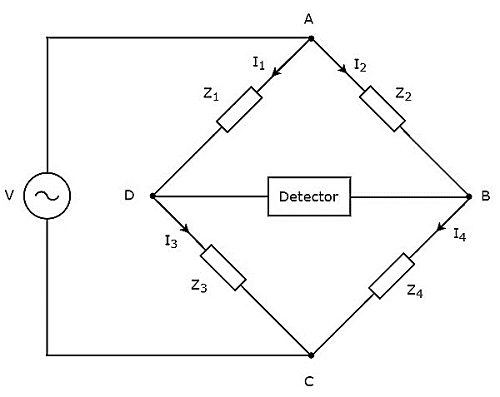
위의 그림과 같이 AC 브리지는 주로 4 개의 암으로 구성되며 마름모 또는 square shape. 이 모든 암은 임피던스로 구성됩니다.
알 수없는 임피던스 값을 찾으려면 감지기와 AC 전압 소스도 필요합니다. 따라서이 두 개 중 하나는 AC 브리지의 한 대각선에 배치되고 다른 하나는 AC 브리지의 다른 대각선에 배치됩니다. 휘트 스톤 다리의 균형 상태는-
$$ R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $$
우리는 얻을 것입니다 balancing condition of AC bridge, 위 방정식에서 R을 Z로 바꾸면됩니다.
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$ \ Rightarrow Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $
여기서 $ Z_ {1} $ 및 $ Z_ {2} $는 고정 임피던스입니다. 반면 $ Z_ {3} $는 표준 가변 임피던스이고 $ Z_ {4} $는 알 수없는 임피던스입니다.
Note −이 4 가지 임피던스 중 두 가지를 고정 임피던스로 선택할 수 있습니다. 하나는 표준 가변 임피던스로, 다른 하나는 알 수없는 임피던스로 애플리케이션에 따라 선택할 수 있습니다.
다음은 측정에 사용할 수있는 두 개의 AC 브리지입니다. inductance.
- 맥스웰의 다리
- 헤이즈 브리지
이제이 두 AC 브리지에 대해 하나씩 살펴 보겠습니다.
맥스웰의 다리
Maxwell의 브리지는 4 개의 암이있는 AC 브리지로, 마름모 또는 square shape. 이 브리지의 두 암은 단일 저항으로 구성되고 한 암은 저항과 인덕터의 직렬 조합으로 구성되고 다른 암은 저항과 커패시터의 병렬 조합으로 구성됩니다.
알 수없는 임피던스 값을 찾기 위해 AC 검출기와 AC 전압 소스가 사용됩니다. 따라서이 둘 중 하나는 Maxwell 다리의 대각선 하나에 배치되고 다른 하나는 Maxwell 다리의 다른 대각선에 배치됩니다.
Maxwell의 브리지는 중간 인덕턴스 값을 측정하는 데 사용됩니다. 그만큼circuit diagram Maxwell의 다리는 아래 그림과 같습니다.
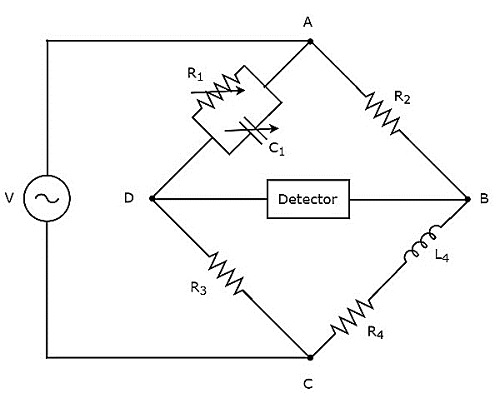
위의 회로에서 암 AB, BC, CD 및 DA는 함께 마름모 또는 정사각형 모양을 형성합니다. 암 AB와 CD는 각각 $ R_ {2} $ 및 $ R_ {3} $ 저항으로 구성됩니다. 암 BC는 저항 $ R_ {4} $와 인덕터 $ L_ {4} $의 직렬 조합으로 구성됩니다. 암, DA는 저항기 $ R_ {1} $ 및 커패시터 $ C_ {1} $의 병렬 조합으로 구성됩니다.
$ Z_ {1}, Z_ {2}, Z_ {3} $ 및 $ Z_ {4} $가 각각 암 DA, AB, CD 및 BC의 임피던스라고합시다. 그만큼values of these impedances 될거야
$$ Z_ {1} = \ frac {R_ {1} \ left (\ frac {1} {j \ omega C_ {1}} \ right)} {R_ {1} + \ frac {1} {j \ omega C_ {1}}} $$
$$ \ Rightarrow Z_ {1} = \ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}} $$
$ Z_ {2} = R_ {2} $
$ Z_ {3} = R_ {3} $
$ Z_ {4} = R_ {4} + j \ omega L_ {4} $
Substitute AC 브리지의 다음 균형 조건에서 이러한 임피던스 값.
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ 왼쪽 ({\ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}} \ 오른쪽)} $$
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} \ left (1 + j \ omega R_ {1} C_ {1} \ right)} {R_ { 1}} $
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + \ frac {j \ omega R_ {1} C_ {1} R_ {2} R_ {3}} {R_ {1}} $
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + j \ omega C_ {1} R_ {2} R_ {3} $
으로 comparing 위 방정식의 각각의 실수 및 허수 항, 우리는
$ R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $ 방정식 1
$ L_ {4} = C_ {1} R_ {2} R_ {3} $ 방정식 2
방정식 1에서 저항기 $ R_ {1} $, $ R_ {2} $ 및 $ R_ {3} $의 값을 대체하여 저항기 $ R_ {4} $의 값을 얻습니다. 마찬가지로 방정식 2에서 커패시터 값 $ C_ {1} $와 저항 값 $ R_ {2} $ 및 $ R_ {3} $를 대입하여 인덕터 값 $ L_ {4를 얻습니다. } $.
그만큼 advantage Maxwell의 브리지에서 저항 값 $ R_ {4} $와 인덕터 $ L_ {4} $는 주파수 값과 무관하다는 것입니다.
헤이즈 브리지
Hay 's bridge는 Maxwell 브리지의 수정 된 버전으로, Maxwell 브리지의 저항과 커패시터의 직렬 조합으로 구성된 저항과 커패시터의 병렬 조합으로 구성된 암을 수정하여 얻습니다.
Hay 's bridge는 높은 인덕턴스 값을 측정하는 데 사용됩니다. 그만큼circuit diagram Hay 's bridge의 모습은 아래 그림과 같습니다.
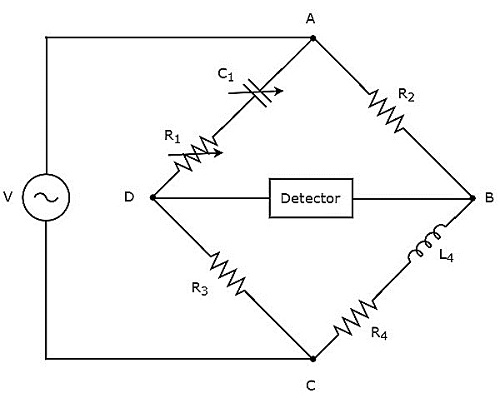
위의 회로에서 암 AB, BC, CD 및 DA는 함께 마름모 또는 정사각형 모양을 형성합니다. 암, AB 및 CD는 각각 $ R_ {2} $ 및 $ R_ {3} $ 저항으로 구성됩니다. 암 BC는 저항 $ R_ {4} $와 인덕터 $ L_ {4} $의 직렬 조합으로 구성됩니다. 팔, DA는 저항기 $ R_ {1} $ 및 커패시터 $ C_ {1} $의 직렬 조합으로 구성됩니다.
$ Z_ {1}, Z_ {2}, Z_ {3} $ 및 $ Z_ {4} $가 각각 암 DA, AB, CD 및 BC의 임피던스라고합시다. 그만큼values of these impedances 될거야
$$ Z_ {1} = R_ {1} + \ frac {1} {j \ omega C_ {1}} $$
$ \ Rightarrow Z_ {1} = \ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} $
$ Z_ {2} = R_ {2} $
$ Z_ {3} = R_ {3} $
$ Z_ {4} = R_ {4} + j \ omega L_ {4} $
Substitute AC 브리지의 다음 균형 조건에서 이러한 임피던스 값.
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ left (\ frac {1 + j \ omega R_ {1} C_ {1}} {j \ 오메가 C_ {1}} \ 오른쪽)} $
$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ left (1 + j \ omega R_ {1} C_ {1} \ 오른쪽)} $
위 방정식의 우변 항의 분자와 분모에 $ 1-j \ omega R_ {1} C_ {1} $를 곱합니다.
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ left (1 + j \ omega R_ {1} C_ { 1} \ right)} \ times \ frac {\ left (1-j \ omega R_ {1} C_ {1} \ right)} {\ left (1-j \ omega R_ {1} C_ {1} \ right )} $
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3} + j \ 오메가 R_ {2} R_ {3} C_ {1}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} $
으로 comparing 위 방정식의 각각의 실수 및 허수 항, 우리는
$ R_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} $ 방정식 3
$ L_ {4} = \ frac {R_ {2} R_ {3} C_ {1}} {\ 왼쪽 (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} $ 방정식 4
방정식 3과 방정식 4에서 $ R_ {1}, R_ {2}, R_ {3}, C_ {1} $ 및 $ \ omega $의 값을 대입하여 저항기 $ R_ {4의 값을 얻습니다. } $ 및 인덕터, $ L_ {4} $.
이전 장에서 인덕턴스를 측정하는 데 사용할 수있는 두 개의 AC 브리지에 대해 논의했습니다. 이 장에서는 다음에 대해 논의하겠습니다.two AC bridges.
- Schering Bridge
- 빈의 다리
이 두 브리지는 각각 커패시턴스와 주파수를 측정하는 데 사용할 수 있습니다.
Schering Bridge
Schering 브리지는 4 개의 암이있는 AC 브리지로, 마름모 또는 square shape, 한쪽 암은 단일 저항으로 구성되고, 한쪽 암은 저항과 커패시터의 직렬 조합으로 구성되며, 한쪽 암은 단일 커패시터로 구성되고 다른 암은 저항과 커패시터의 병렬 조합으로 구성됩니다.
AC 검출기와 AC 전압 소스는 또한 알려지지 않은 임피던스의 값을 찾는 데 사용되므로 그중 하나는 Schering 브리지의 한 대각선에 배치되고 다른 하나는 Schering 브리지의 다른 대각선에 배치됩니다.
Schering 브리지는 커패시턴스 값을 측정하는 데 사용됩니다. 그만큼circuit diagram Schering 다리의 모습은 아래 그림과 같습니다.
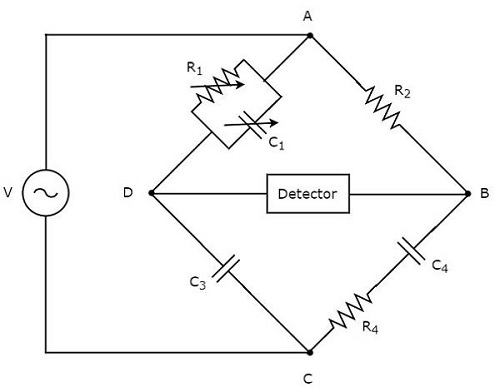
위의 회로에서 AB, BC, CD 및 DA 암은 함께 마름모 또는 square shape. 암 AB는 저항기 $ R_ {2} $로 구성됩니다. 암 BC는 저항 $ R_ {4} $와 커패시터 $ C_ {4} $의 직렬 조합으로 구성됩니다. 암 CD는 커패시터 $ C_ {3} $로 구성됩니다. 암 DA는 저항 $ R_ {1} $ 및 커패시터 $ C_ {1} $의 병렬 조합으로 구성됩니다.
$ Z_ {1} $, $ Z_ {2} $, $ Z_ {3} $ 및 $ Z_ {4} $가 각각 암 DA, AB, CD 및 BC의 임피던스라고합시다. 그만큼values of these impedances 될거야
$ Z_ {1} = \ frac {R_ {1} \ left (\ frac {1} {j \ omega C_ {1}} \ right)} {R_ {1} + \ frac {1} {j \ omega C_ {1}}} $
$ \ Rightarrow Z_ {1} = \ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}} $
$ Z_ {2} = R_ {2} $
$ Z_ {3} = \ frac {1} {j \ omega C_ {3}} $
$ Z_ {4} = R_ {4} + \ frac {1} {j \ omega C_ {4}} $
$ \ Rightarrow Z_ {4} = \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} $
Substitute AC 브리지의 다음 균형 조건에서 이러한 임피던스 값.
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$$ \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} = \ frac {R_ {2} \ left (\ frac {1} {j \ omega C_ { 3}} \ 오른쪽)} {\ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}} $$
$ \ Rightarrow \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} = \ frac {R_ {2} \ left (1 + j \ omega R_ {1} C_ {1} \ 오른쪽)} {j \ omega R_ {1} C_ {3}} $
$ \ Rightarrow \ frac {1 + j \ omega R_ {4} C_ {4}} {C_ {4}} = \ frac {R_ {2} \ left (1 + j \ omega R_ {1} C_ {1} \ 오른쪽)} {R_ {1} C_ {3}} $
$ \ Rightarrow \ frac {1} {C_ {4}} + j \ omega R_ {4} = \ frac {R_ {2}} {R_ {1} C_ {3}} + \ frac {j \ omega C_ { 1} R_ {2}} {C_ {3}} $
으로 comparing 위 방정식의 각각의 실수 및 허수 항, 우리는
$ C_ {4} = \ frac {R_ {1} C_ {3}} {R_ {2}} $ 방정식 1
$ R_ {4} = \ frac {C_ {1} R_ {2}} {C_ {3}} $ 방정식 2
방정식 1에서 $ R_ {1}, R_ {2} $ 및 $ C_ {3} $의 값을 대체하여 커패시터 값 $ C_ {4} $를 얻습니다. 마찬가지로 방정식 2에서 $ R_ {2}, C_ {1} $ 및 $ C_ {3} $의 값을 대입하여 저항 값 $ R_ {4} $를 얻습니다.
그만큼 advantage Schering 브리지의 경우 저항 값 $ R_ {4} $ 및 커패시터 $ C_ {4} $가 주파수 값과 무관하다는 것입니다.
빈의 다리
Wien’s bridge4 개의 암이있는 AC 브리지로, 마름모 또는 정사각형 형태로 연결됩니다. 두 팔 중 하나의 저항으로 구성되고, 한 팔은 저항과 커패시터의 병렬 조합으로 구성되고 다른 팔은 저항과 커패시터의 직렬 조합으로 구성됩니다.
주파수 값을 찾으려면 AC 검출기와 AC 전압 소스도 필요합니다. 따라서이 두 개 중 하나는 Wien 다리의 한 대각선에 배치되고 다른 하나는 Wien 다리의 다른 대각선에 배치됩니다.
그만큼 circuit diagram 아래 그림은 빈의 다리의 모습입니다.
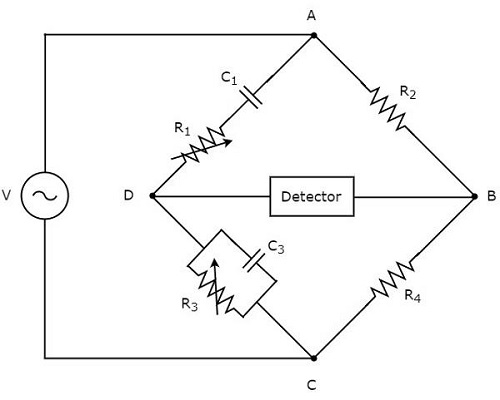
위의 회로에서 AB, BC, CD 및 DA 암은 함께 마름모 또는 square shape. 암 AB 및 BC는 각각 $ R_ {2} $ 및 $ R_ {4} $ 저항으로 구성됩니다. 암, CD는 저항 $ R_ {3} $와 커패시터 $ C_ {3} $의 병렬 조합으로 구성됩니다. 팔, DA는 저항기 $ R_ {1} $ 및 커패시터 $ C_ {1} $의 직렬 조합으로 구성됩니다.
$ Z_ {1}, Z_ {2}, Z_ {3} $ 및 $ Z_ {4} $가 각각 암 DA, AB, CD 및 BC의 임피던스라고합시다. 그만큼values of these impedances 될거야
$$ Z_ {1} = R_ {1} + \ frac {1} {j \ omega C_ {1}} $$
$$ \ Rightarrow Z_ {1} = \ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} $$
$ Z_ {2} = R_ {2} $
$$ Z_ {3} = \ frac {R_ {3} \ left (\ frac {1} {j \ omega C_ {3}} \ right)} {R_ {3} + \ frac {1} {j \ omega C_ {3}}} $$
$$ \ 오른쪽 화살표 Z_ {3} = \ frac {R_ {3}} {1 + j \ omega R_ {3} C_ {3}} $$
$ Z_ {4} = R_ {4} $
Substitute AC 브리지의 다음 균형 조건에서 이러한 임피던스 값.
$$ Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $$
$$ \ 왼쪽 (\ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} \ 오른쪽) R_ {4} = R_ {2} \ 왼쪽 (\ frac {R_ {3}} {1 + j \ omega R_ {3} C_ {3}} \ 오른쪽) $$
$ \ Rightarrow \ left (1 + j \ omega R_ {1} C_ {1} \ right) \ left (1 + j \ omega R_ {3} C_ {3} \ right) R_ {4} = j \ omega C_ {1} R_ {2} R_ {3} $
$ \ Rightarrow \ left (1 + j \ omega R_ {3} C_ {3} + j \ omega R_ {1} C_ {1}-\ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ 오른쪽) R_ {4} = j \ omega C_ {1} R_ {2} R_ {3} $
$ \ Rightarrow R_ {4} \ left (\ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ right) + j \ omega R_ {4} \ left (R_ {3} C_ {3} + R_ {1} C_ {1} \ right) = j \ omega C_ {1} R_ {2} R_ {3} $
Equate 각각 real terms 위 방정식의.
$$ R_ {4} \ 왼쪽 (1- \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ 오른쪽) = 0 $$
$ \ Rightarrow 1- \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} = 0 $
$ \ Rightarrow 1 = \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} $
$ \ omega = \ frac {1} {\ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}} $
Substitute, $ \ omega = 2 \ pi f $ 위 방정식에서.
$$ \ Rightarrow 2 \ pi f = \ frac {1} {\ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}} $$
$ \ Rightarrow f = \ frac {1} {2 \ pi \ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}} $
위 방정식에서 $ R_ {1}, R_ {3}, C_ {1} $ 및 $ C_ {3} $의 값을 대체하여 주파수 값, AC 전압 소스의 $ f $를 찾을 수 있습니다.
$ R_ {1} = R_ {3} = R $ 및 $ C_ {1} = C_ {3} = C $이면 다음 공식을 사용하여 주파수 값, AC 전압 소스의 $ f $를 찾을 수 있습니다. .
$$ f = \ frac {1} {2 \ pi RC} $$
Wein의 다리는 주로 frequency value AF 범위.
기본적으로 Transducer는 한 형태의 에너지를 다른 형태의 에너지로 변환합니다. 비전 기적 형태의 에너지를 전기적 형태의 에너지로 변환하는 변환기는 다음과 같이 알려져 있습니다.electrical transducer. 그만큼block diagram 전기 변환기의 그림은 아래 그림과 같습니다.
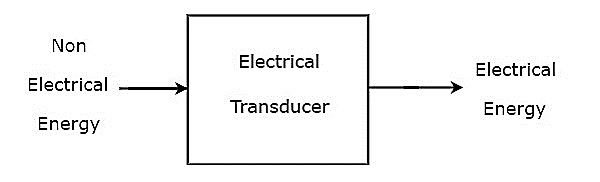
그림과 같이 전기 변환기는 전기 에너지가있는 출력을 생성합니다. 전기 변환기의 출력은 전기가 아닌 에너지를 가진 입력과 동일합니다.
전기 변환기의 유형
주로 전기 변환기는 다음과 같이 분류 할 수 있습니다. two types.
- 활성 변환기
- 패시브 트랜스 듀서
이제이 두 가지 유형의 변환기에 대해 간략히 설명하겠습니다.
활성 변환기
전압 및 전류와 같은 전기량 중 하나를 생성 할 수있는 변환기는 다음과 같이 알려져 있습니다. active transducer. 외부 전원 공급이 필요하지 않기 때문에 자체 생성 변환기라고도합니다.
그만큼 block diagram 활성 변환기의 수는 아래 그림과 같습니다.
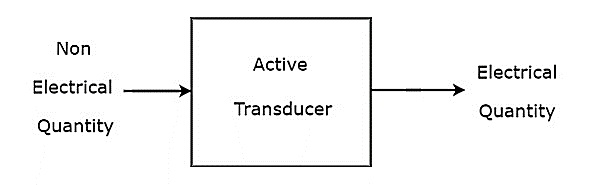
그림에 표시된 것처럼 활성 변환기는 전기적 양 (또는 신호)을 생성하며, 이는 비전 기적 입력 양 (또는 신호)과 동일합니다.
Examples
다음은 활성 변환기의 예입니다.
- 피에조 전기 변환기
- 광전 변환기
- 열전 변환기
다음 장에서 이러한 활성 변환기에 대해 논의 할 것입니다.
패시브 트랜스 듀서
전압 및 전류와 같은 전기량을 생성 할 수없는 변환기는 다음과 같이 알려져 있습니다. passive transducer. 그러나 저항 (R), 인덕터 (L) 및 커패시터 (C)와 같은 수동 소자 중 하나에서 변동을 생성합니다. 패시브 변환기에는 외부 전원 공급이 필요합니다.
그만큼 block diagram 패시브 트랜스 듀서는 아래 그림과 같습니다.
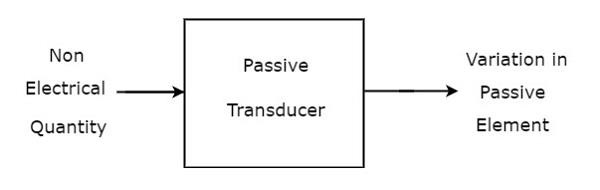
그림에서 볼 수 있듯이 수동 변환기는 비전 기적 입력량 (또는 신호)의 변화에 따라 수동 소자의 변화를 생성합니다.
Examples
다음은 패시브 트랜스 듀서의 예입니다.
- 저항성 변환기
- 유도 변환기
- 용량 성 변환기
이 패시브 트랜스 듀서에 대해서는 이후 장에서 설명하겠습니다.
Active transducer비 전기적 양을 전기적 양으로 변환하는 변환기입니다. 압력, 조명 및 온도와 같은 비 전기적 양을 고려해 보겠습니다. 따라서 우리가 선택한 비 전기적 양에 따라 다음 세 가지 활성 변환기를 얻을 수 있습니다.
- 피에조 전기 변환기
- 광전 변환기
- 열전 변환기
이제이 세 가지 활성 변환기에 대해 하나씩 논의하겠습니다.
피에조 전기 변환기
활성 변환기는 piezo electric transducer, 압력 입력과 동일한 전기량을 생성 할 때. 다음 세 가지 물질은 압전 효과를 나타냅니다.
- Quartz
- 로셸 소금
- Tourmaline
이 세 가지 물질이 보여주는 압전 효과는이 오름차순으로 토르말린, 석영 및 로셸 염입니다. 이 세 가지 물질이 갖는 기계적 강도의 오름차순은 Rochelle salts, Quartz, Tourmaline입니다.
Quartz 이 세 가지 피에조 전기 물질 중 적당한 피에조 전기 효과를 나타내며 적당한 기계적 강도를 나타내어 피에조 전기 변환기로 사용됩니다.
석영 변환기
그만큼 circuit diagramQuartz Transducer의 그림은 아래와 같습니다. 그림과 같이 수정은베이스와 힘 합산 부재 사이에 위치합니다. 출력 전압은 수정의 양면에 위치한 금속 전극을 통해 측정 할 수 있습니다.
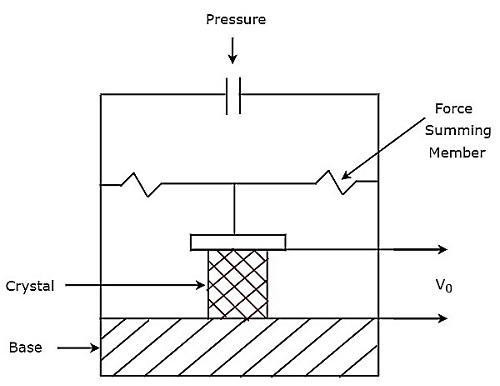
그만큼 output voltage, 위 압력 변환기의 $ V_ {0} $는
$$ V_ {0} = \ frac {Q} {C} $$
광전 변환기
능동형 변환기는 광 입력의 조명과 동일한 전기량을 생성 할 때 광전 변환기라고합니다. 그만큼circuit diagram 광전 변환기의 그림은 아래 그림과 같습니다.
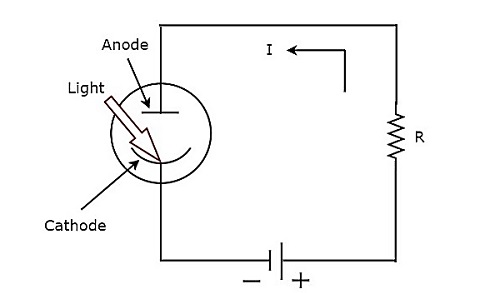
그만큼 working 광전 변환기의 설명은 아래와 같습니다.
Step1 − 광전 변환기는 빛이 음극에 떨어지면 전자를 방출합니다.
Step2 − 광전 변환기는 전자가 양극으로 끌어 당겨 회로에서 전류 I를 생성합니다.
우리는 찾을 수 있습니다 sensitivity 다음 공식을 사용하여 광전 변환기의.
$$ S = \ frac {I} {i} $$
어디,
$ S $는 광전 변환기의 감도입니다.
$ I $는 광전 변환기의 출력 전류입니다.
$ i $는 광전 변환기의 입력 광 조명입니다.
열전 변환기
활성 변환기는 thermo electric transducer, 온도 입력과 동일한 전기량을 생성 할 때. 다음 두 변환기는 열전 변환기의 예입니다.
- 서미스터 변환기
- 열전대 변환기
이제이 두 변환기에 대해 하나씩 살펴 보겠습니다.
서미스터 변환기
온도에 의존하는 저항을 열 저항이라고합니다. 간단히 말해Thermistor. 서미스터의 온도 계수는 음수입니다. 즉, 온도가 증가하면 서미스터의 저항이 감소합니다.
Mathematically, 서미스터의 저항과 온도의 관계는 다음과 같이 나타낼 수 있습니다.
$$ R_ {1} = R_ {2} e ^ \ left (\ beta \ left [\ frac {1} {T_ {1}}-\ frac {1} {T_ {2}} \ right] \ right) $$
Where,
$ R_ {1} $는 $ {T_ {1}} ^ {0} K $ 온도에서의 서미스터 저항입니다.
$ R_ {2} $는 $ {T_ {2}} ^ {0} K $ 온도에서의 서미스터 저항입니다.
$ \ beta $는 온도 상수입니다.
그만큼 advantage 서미스터 변환기의 특징은 빠르고 안정적인 응답을 생성한다는 것입니다.
열전대 변환기
열전쌍 변환기는 입력에서 해당 온도 변화에 대한 출력 전압을 생성합니다. 두 개의 접합을 만들기 위해 서로 다른 금속의 두 와이어를 함께 결합하면 전체 구성이 호출됩니다.Thermocouple. 기본 열전대의 회로도는 다음과 같습니다.
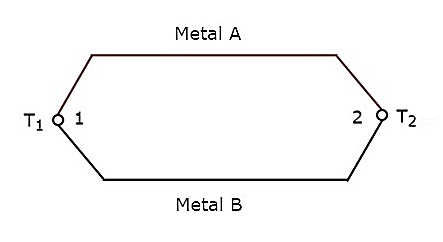
위의 열전대에는 두 개의 금속 A와 B와 두 개의 접합부 1과 2가 있습니다. 접합부 2에서 일정한 기준 온도 $ T_ {2} $를 고려하십시오. 접합부 1의 온도를 $ T_ {1} $로 설정하십시오. 열전대는emf (기전력) $ T_ {1} $ 및 $ T_ {2} $의 값이 다를 때마다.
즉, 열전대는 두 접합점 1과 2 사이에 온도 차이가있을 때마다 EMF를 생성하고 두 접합점 사이의 온도 차이에 정비례합니다. Mathematically, 다음과 같이 나타낼 수 있습니다.
$$ e \ alpha \ 왼쪽 (T_ {1} -T_ {2} \ 오른쪽) $$
어디,
$ e $는 열전대에 의해 생성 된 EMF입니다.
위의 열전쌍 회로는 실제 응용을 위해 아래 그림과 같이 나타낼 수 있습니다.
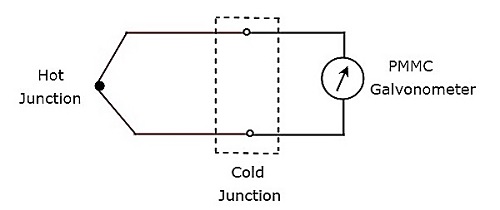
이 두 접합부를 포함하여 열 접점과 냉 접점 사이에있는 회로 부분은 기본 열전대의 동일한 모델입니다. PMMC 검류계는 냉 접점을 가로 질러 연결되고 냉 접점에서 생성 된 EMF에 따라 편향됩니다.Thermocouple transducer 가장 일반적으로 사용되는 열전 변환기입니다.
passive transducer수동 소자의 변화를 생성하는 변환기입니다. 저항, 인덕터 및 커패시터와 같은 수동 소자를 고려할 것입니다. 따라서 우리가 선택한 수동 요소에 따라 다음 세 가지 수동 변환기를 얻을 수 있습니다.
- 저항성 변환기
- 유도 변환기
- 용량 성 변환기
이제이 세 가지 수동 변환기에 대해 하나씩 논의 해 보겠습니다.
저항성 변환기
패시브 트랜스 듀서는 resistive transducer, 저항 값의 변동 (변화)을 생성 할 때. 다음 공식resistance, 금속 도체의 R.
$$ R = \ frac {\ rho \ : l} {A} $$
어디,
$ \ rho $는 도체의 저항률입니다.
$ l $는 지휘자의 길이
$ A $는 지휘자의 단면적입니다.
저항 값은 $ \ rho, l $ 및 $ A $의 세 가지 매개 변수에 따라 다릅니다. 그래서 우리는resistive transducers세 가지 매개 변수 $ \ rho, l $ & $ A $ 중 하나의 변형을 기반으로합니다. 이 세 가지 매개 변수 중 하나의 변화는 저항 값을 변경합니다.
저항, R은 resistivity지휘자의 $ \ rho $. 따라서 도체의 저항률이 $ \ rho $이면 저항 값이 증가하고 R도 증가합니다. 마찬가지로 도체의 저항률로 $ \ rho $는 저항 값을 감소시키고 R도 감소합니다.
저항, R은 length지휘자, $ l $. 따라서 도체의 길이가 $ l $이면 저항 값이 증가하고 R도 증가합니다. 마찬가지로 도체의 길이가 $ l $이면 저항 값이 감소하고 R도 감소합니다.
저항, R은에 반비례합니다. cross sectional area지휘자의 $ A $. 따라서 도체의 단면적이 $ A $이면 저항 값이 증가하고 R은 감소합니다. 마찬가지로 도체의 단면적이 $ A $이면 저항 값이 감소하고 R은 증가합니다.
유도 변환기
패시브 트랜스 듀서는 inductive transducer, 인덕턴스 값의 변화 (변화)를 생성 할 때. 다음 공식inductance, 인덕터의 L.
$ L = \ frac {N ^ {2}} {S} $ 방정식 1
어디,
$ N $는 코일의 회전 수입니다.
$ S $는 코일의 회전 수입니다.
다음 공식 reluctance, 코일의 S.
$ S = \ frac {l} {\ mu A} $ 방정식 2
어디,
$ l $는 자기 회로의 길이입니다.
$ \ mu $는 코어의 투자율입니다.
$ A $는 자속이 흐르는 자기 회로의 영역입니다.
방정식 1의 방정식 2를 대체합니다.
$$ L = \ frac {N ^ {2}} {\ left (\ frac {l} {\ mu A} \ right)} $$
$ \ Rightarrow L = \ frac {N ^ {2} \ mu A} {l} $ 방정식 3
방정식 1과 방정식 3에서 인덕턴스 값이 세 가지 매개 변수 $ N, S $ 및 $ \ mu $에 따라 달라진다는 결론을 내릴 수 있습니다. 그래서 우리는inductive transducers세 가지 매개 변수 $ N, S $ & $ \ mu $ 중 하나의 변동을 기반으로합니다. 왜냐하면이 세 가지 매개 변수 중 하나의 변화는 인덕턴스 값을 변경하기 때문입니다.
인덕턴스, L은 제곱에 정비례합니다. number of turns of coil. 따라서 코일의 권선 수에 따라 $ N $는 인덕턴스 값을 증가시키고 $ L $도 증가합니다. 마찬가지로 코일의 권선 수에 따라 $ N $는 인덕턴스 값을 감소시키고 $ L $도 감소합니다.
인덕턴스, $ L $는 다음 값에 반비례합니다. reluctance of coil, $ S $. 따라서 코일의 저항에 따라 $ S $는 인덕턴스 값을 증가시키고 $ L $는 감소합니다. 유사하게 코일의 저항에 따라 $ S $는 인덕턴스 값을 감소시키고 $ L $는 증가합니다.
인덕턴스, L은 다음에 정비례합니다. permeability of core, $ \ mu $. 따라서 코어의 투자율이 $ \ mu $이면 인덕턴스 값이 증가하고 L도 증가합니다. 마찬가지로 코어의 투자율이 $ \ mu $이면 인덕턴스 값이 감소하고 L도 감소합니다.
용량 성 변환기
패시브 트랜스 듀서는 capacitive transducer, 커패시턴스 값의 변화 (변화)를 생성 할 때. 다음 공식capacitance, C 병렬 플레이트 커패시터.
$$ C = \ frac {\ varepsilon A} {d} $$
어디,
$ \ varepsilon $은 유전율 또는 유전 상수입니다.
$ A $는 두 접시의 유효 면적입니다.
$ d $는 두 접시의 유효 면적입니다.
커패시턴스 값은 $ \ varepsilon, A $ 및 $ d $의 세 가지 매개 변수에 따라 다릅니다. 그래서 우리는capacitive transducers세 가지 매개 변수 $ \ varepsilon, A $ & $ d $ 중 하나의 변형을 기반으로합니다. 왜냐하면이 세 가지 매개 변수 중 하나의 변화는 커패시턴스 값을 변경하기 때문입니다.
커패시턴스, C는 다음에 직접 비례합니다. permittivity, $ \ varepsilon $. 따라서 유전율로 $ \ varepsilon $은 커패시턴스 값을 증가시키고 C도 증가합니다. 마찬가지로 유전율로 $ \ varepsilon $은 커패시턴스 값을 감소시키고 C도 감소합니다.
커패시턴스, C는 effective area of two plates, $ A $. 따라서 두 플레이트의 유효 면적이 $ A $이면 커패시턴스 값이 증가하고 C도 증가합니다. 마찬가지로, 두 플레이트의 유효 면적이 $ A $이면 커패시턴스 값이 감소하고 C도 감소합니다.
커패시턴스, C는에 반비례합니다. distance between two plates, $ d $. 따라서 두 플레이트 사이의 거리에 따라 $ d $가 커패시턴스 값을 증가시키고 C는 감소합니다. 마찬가지로 두 플레이트 사이의 거리가 $ d $이면 커패시턴스 값이 감소하고 C가 증가합니다.
이 장에서는 세 가지 패시브 트랜스 듀서에 대해 논의했습니다. 다음 장에서는 각 수동 변환기의 예에 대해 논의하겠습니다.
그만큼 physical quantities변위, 속도, 힘, 온도 등은 모두 전기가 아닌 양입니다. 능동형 변환기는 물리량을 전기 신호로 변환합니다. 반면, 수동 변환기는 물리량을 수동 요소의 변화로 변환합니다.
따라서 요구 사항에 따라 능동형 변환기 또는 수동형 변환기를 선택할 수 있습니다. 이 장에서는 패시브 변환기를 사용하여 변위를 측정하는 방법에 대해 설명합니다. 한 지점에서 다른 지점으로 직선으로 이동하는 몸체가 있으면 두 지점 사이의 길이를displacement.
우리는 다음이 있습니다 three passive transducers
- 저항성 변환기
- 유도 변환기
- 용량 성 변환기
이제이 세 개의 수동 변환기를 하나씩 사용하여 변위 측정에 대해 논의 해 보겠습니다.
저항성 변환기를 사용한 변위 측정
그만큼 circuit diagram 변위를 측정하는 데 사용되는 저항 변환기의 그림은 아래 그림과 같습니다.
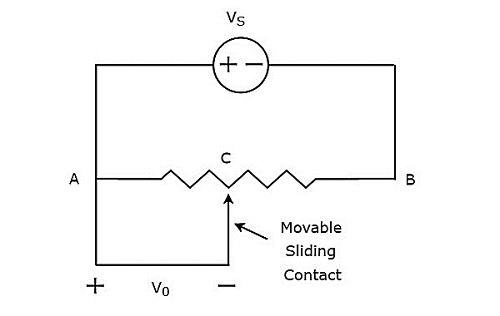
위의 회로는 전위차계와 전압 소스 $ V_ {S} $로 구성됩니다. 이 두 가지가 A와 B 지점에 대해 병렬로 연결되어 있다고 말할 수 있습니다. 전위차계에는 슬라이딩 접점이 있으며 변경 될 수 있습니다. 따라서 점 C는 변수 1입니다. 위의 회로에서output voltage, $ V_ {0} $는 A와 C 지점에서 측정됩니다.
Mathematically, 전압과 거리 사이의 관계는 다음과 같이 나타낼 수 있습니다.
$$ \ frac {V_ {0}} {V_ {S}} = \ frac {AC} {AB} $$
따라서 변위를 측정 할 몸체를 슬라이딩 접점에 연결해야합니다. 따라서 몸이 직선으로 움직일 때마다 점 C도 변합니다. 이로 인해 출력 전압 $ V_ {0} $도 그에 따라 변경됩니다.
이 경우 출력 전압 $ V_ {0} $를 측정하여 변위를 찾을 수 있습니다.
유도 형 변환기를 사용한 변위 측정
그만큼 circuit diagram 변위를 측정하는 데 사용되는 유도 변환기의 그림은 다음과 같습니다.
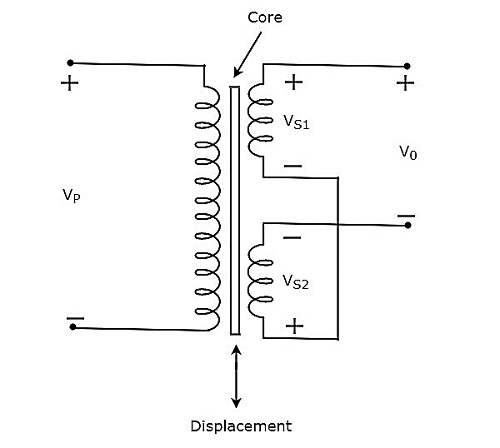
위의 회로에있는 변압기에는 1 차 권선과 2 차 권선이 있습니다. 여기서 두 개의 2 차 권선의 끝점은 함께 결합됩니다. 따라서이 두 개의 2 차 권선이series opposition.
전압 $ V_ {P} $는 변압기의 1 차 권선에 적용됩니다. 각 2 차 권선에서 발생하는 전압은 ð ?? '‰ ð ??'† 1 및 ð ?? '‰ ð ??'† 2입니다. 출력 전압 $ V_ {0} $는 두 개의 2 차 권선의 시작점에서 사용됩니다.
Mathematically, 출력 전압 ð ?? '‰ 0은 다음과 같이 쓸 수 있습니다.
$$ V_ {0} = V_ {S1} -V_ {S2} $$
위의 회로에 존재하는 변압기는 differential transformer, $ V_ {S1} $와 $ V_ {S2} $의 차이 인 출력 전압을 생성하기 때문입니다.
코어가 중앙 위치에 있으면 출력 전압 $ V_ {0} $는 0과 같습니다. 왜냐하면 $ V_ {S1} $ 및 $ V_ {S2} $의 각 크기 및 위상이 동일하기 때문입니다.
코어가 중앙 위치에 있지 않으면 출력 전압 $ V_ {0} $에 크기와 위상이 어느 정도 있습니다. 왜냐하면 $ V_ {S1} $와 $ V_ {S2} $의 각각의 크기와 위상이 같지 않기 때문입니다.
따라서 변위를 측정 할 몸체를 중심 코어에 연결해야합니다. 따라서 몸이 직선으로 움직일 때마다 코어의 중심 위치가 달라집니다. 이로 인해 출력 전압 $ V_ {0} $도 그에 따라 변경됩니다.
이 경우 우리는 displacement출력 전압 $ V_ {0} $를 측정합니다. 출력 전압의 크기 및 위상 $ V_ {0} $는 각각 신체의 변위와 방향을 나타냅니다.
용량 성 변환기를 사용한 변위 측정
그만큼 circuit diagram 변위를 측정하는 데 사용되는 용량 성 변환기의 그림은 아래 그림과 같습니다.
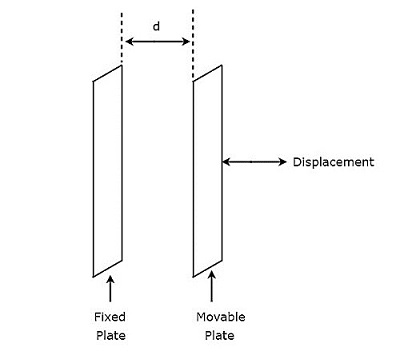
그만큼 capacitor, 위의 회로에 존재하는 두 개의 평행 판이 있습니다. 그중 하나는 고정되어 있고 다른 하나는 움직일 수있는 것이다. 이로 인해이 두 플레이트 사이의 간격도 달라집니다. 커패시터의 두 판 사이의 간격이 변경됨에 따라 커패시턴스 값이 변경됩니다.
그러므로 우리는 displacement축전기의 가동 판까지 측정되어야합니다. 따라서 몸체가 직선으로 움직일 때마다 두 개의 커패시터 판 사이의 간격이 달라집니다. 이로 인해 커패시턴스 값이 변경됩니다.
데이터 수집에 사용되는 시스템은 다음과 같이 알려져 있습니다. data acquisition systems. 이러한 데이터 수집 시스템은 데이터 변환, 데이터 저장, 데이터 전송 및 데이터 처리와 같은 작업을 수행합니다.
데이터 수집 시스템은 다음 사항을 고려합니다. analog signals.
DC 및 AC 전압, DC 및 AC 전류, 저항 등과 같은 전기량을 직접 측정하여 얻은 아날로그 신호
LVDT, Thermocouple 등과 같은 변환기에서 얻은 아날로그 신호
데이터 수집 시스템의 유형
데이터 수집 시스템은 다음과 같이 분류 할 수 있습니다. two types.
- 아날로그 데이터 수집 시스템
- 디지털 데이터 수집 시스템
이제이 두 가지 유형의 데이터 수집 시스템에 대해 하나씩 살펴 보겠습니다.
아날로그 데이터 수집 시스템
아날로그 신호로 작동 할 수있는 데이터 수집 시스템은 analog data acquisition systems. 다음은 아날로그 데이터 수집 시스템의 블록입니다.
Transducer − 물리량을 전기 신호로 변환합니다.
Signal conditioner − 신호의 원하는 부분을 증폭 및 선택하는 기능을 수행합니다.
Display device − 모니터링을위한 입력 신호를 표시합니다.
Graphic recording instruments − 입력 데이터를 영구적으로 기록하는 데 사용할 수 있습니다.
Magnetic tape instrumentation − 입력 데이터의 획득, 저장 및 재생에 사용됩니다.
디지털 데이터 수집 시스템
디지털 신호로 작동 할 수있는 데이터 수집 시스템은 digital data acquisition systems. 따라서 그들은 정보를 저장하거나 표시하기 위해 디지털 구성 요소를 사용합니다.
주로 다음 operations 디지털 데이터 수집에서 발생합니다.
- 아날로그 신호 수집
- 아날로그 신호를 디지털 신호 또는 디지털 데이터로 변환
- 디지털 신호 또는 디지털 데이터 처리
다음은 블록입니다 Digital data acquisition systems.
Transducer − 물리량을 전기 신호로 변환합니다.
Signal conditioner − 신호의 원하는 부분을 증폭 및 선택하는 기능을 수행합니다.
Multiplexer− 여러 입력 중 하나를 출력에 연결합니다. 따라서 직렬 변환기에 병렬로 작동합니다.
Analog to Digital Converter − 아날로그 입력을 동등한 디지털 출력으로 변환합니다.
Display device − 데이터를 디지털 형식으로 표시합니다.
Digital Recorder − 데이터를 디지털 형식으로 기록하는 데 사용됩니다.
데이터 수집 시스템은 생물 의학 및 항공 우주와 같은 다양한 응용 분야에서 사용되고 있습니다. 따라서 요구 사항에 따라 아날로그 데이터 수집 시스템 또는 디지털 데이터 수집 시스템을 선택할 수 있습니다.