DC 전압계
DC 전압계는 전기 회로의 두 지점에서 DC 전압을 측정하는 데 사용되는 측정 기기입니다. PMMC (Permanent Magnet Moving Coil) 검류계와 직렬로 저항을 배치하면 전체 조합이 다음과 같이 작동합니다.DC voltmeter.
DC 전압계에 사용되는 직렬 저항은 직렬 곱셈기 저항 또는 간단히 곱셈기라고도합니다. 미터 전류가 전체 스케일 편향 값을 초과하는 것을 방지하기 위해 기본적으로 검류계를 통해 흐르는 전류의 양을 제한합니다. 그만큼circuit diagram DC 전압계의 값은 아래 그림과 같습니다.
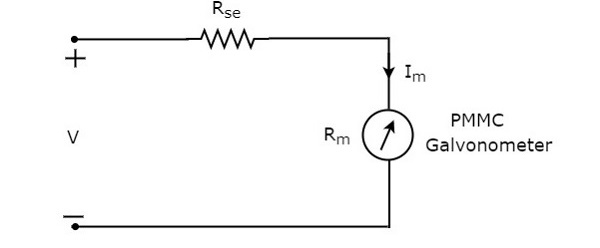
DC 전압이 측정되는 전기 회로의 두 지점에이 DC 전압계를 배치해야합니다.
대다 KVL 위 회로의 루프 주변.
$ V-I_ {m} R_ {se} -I_ {m} R_ {m} = 0 $ (수식 1)
$$ \ 오른쪽 화살표 V-I_ {m} R_ {m} = I_ {m} R_ {se} $$
$$ \ Rightarrow R_ {se} = \ frac {V-I_ {m} R_ {m}} {I_ {m}} $$
$ \ Rightarrow R_ {se} = \ frac {V} {I_ {m}}-R_ {m} $ (수식 2)
어디,
$ R_ {se} $는 계열 승수 저항입니다.
$ V $는 측정 할 전체 범위 DC 전압입니다.
$ I_ {m} $는 풀 스케일 편향 전류입니다.
$ R_ {m} $는 검류계의 내부 저항입니다.
측정 할 전체 범위 DC 전압의 비율 $ V $와 검류계의 DC 전압 강하 $ V_ {m} $는 다음과 같이 알려져 있습니다. multiplying factor, 미디엄. 수학적으로 다음과 같이 나타낼 수 있습니다.
$ m = \ frac {V} {V_ {m}} $ (수식 3)
방정식 1에서 다음 방정식을 얻습니다. full range DC voltage 즉, $ V $입니다.
$ V = I_ {m} R_ {se} + I_ {m} R_ {m} $ (수식 4)
그만큼 DC voltage drop검류계에서 $ V_ {m} $는 풀 스케일 편향 전류 $ I_ {m} $와 검류계의 내부 저항 $ R_ {m} $의 곱입니다. 수학적으로 다음과 같이 쓸 수 있습니다.
$ V_ {m} = I_ {m} R_ {m} $ (수식 5)
Substitute, 방정식 4 및 방정식 3의 방정식 5
$$ m = \ frac {I_ {m} R_ {se} + I_ {m} R_ {m}} {I_ {m} R_ {m}} $$
$ \ Rightarrow m = \ frac {R_ {se}} {R_ {m}} + 1 $
$ \ Rightarrow m-1 = \ frac {R_ {se}} {R_ {m}} $
$ R_ {se} = R_ {m} \ left (m-1 \ right) $ (수식 6)
우리는 찾을 수 있습니다 value of series multiplier resistance 사용 가능한 데이터를 기반으로 방정식 2 또는 방정식 6을 사용합니다.
다중 범위 DC 전압계
이전 섹션에서는 PMMC 검류계와 직렬로 멀티 플라이어 저항을 배치하여 얻은 DC 전압계에 대해 설명했습니다. 이 DC 전압계는particular range DC 전압의.
DC 전압계를 사용하여 DC 전압을 측정하려면 multiple ranges, 그런 다음 단일 승수 저항 대신 여러 개의 병렬 승수 저항을 사용해야하며이 저항의 전체 조합은 PMMC 검류계와 직렬로 연결됩니다. 그만큼circuit diagram 다중 범위 DC 전압계의 그림은 아래 그림과 같습니다.
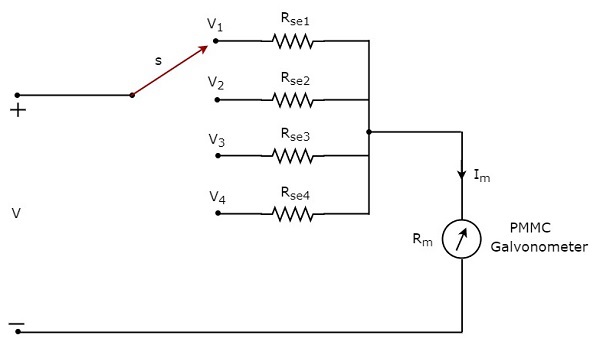
우리는 이것을 배치해야 multi range DC voltmeter필요한 범위의 DC 전압이 측정되는 전기 회로의 두 지점에 걸쳐 있습니다. 스위치 s를 각 곱셈기 저항에 연결하여 원하는 전압 범위를 선택할 수 있습니다.
$ m_ {1}, m_ {2}, m_ {2} $ 및 $ m_ {4} $는 multiplying factors측정 할 전체 범위 DC 전압을 각각 $ V_ {1}, V_ {2}, V_ {3} $ 및 $ V_ {4} $로 고려할 때 DC 전압계의 다음은 각 배율에 해당하는 공식입니다.
$$ m_ {1} = \ frac {V_ {1}} {V_ {m}} $$
$$ m_ {2} = \ frac {V_ {2}} {V_ {m}} $$
$$ m_ {3} = \ frac {V_ {3}} {V_ {m}} $$
$$ m_ {4} = \ frac {V_ {4}} {V_ {m}} $$
위의 회로에는 4 개의 series multiplier resistors, $ R_ {se1}, R_ {se2}, R_ {se3} $ 및 $ R_ {se4} $. 다음은이 네 가지 저항에 해당하는 공식입니다.
$$ R_ {se1} = R_ {m} \ 왼쪽 (m_ {1} -1 \ 오른쪽) $$
$$ R_ {se2} = R_ {m} \ 왼쪽 (m_ {2} -1 \ 오른쪽) $$
$$ R_ {se3} = R_ {m} \ 왼쪽 (m_ {3} -1 \ 오른쪽) $$
$$ R_ {se4} = R_ {m} \ 왼쪽 (m_ {4} -1 \ 오른쪽) $$
따라서 위의 공식을 사용하여 각 직렬 곱셈기 저항의 저항 값을 찾을 수 있습니다.