퍼지 논리-세트 이론

퍼지 세트는 클래식 세트의 확장 및 전체적인 단순화로 간주 될 수 있습니다. 세트 멤버십의 맥락에서 가장 잘 이해할 수 있습니다. 기본적으로 부분 멤버쉽을 허용합니다. 즉, 집합의 멤버쉽 등급이 다른 요소를 포함합니다. 이것으로부터 우리는 클래식 세트와 퍼지 세트의 차이점을 이해할 수 있습니다. 클래식 세트에는 멤버십의 정확한 속성을 충족하는 요소가 포함되어있는 반면 퍼지 세트에는 멤버쉽의 부정확 한 속성을 충족하는 요소가 포함됩니다.

수학적 개념

정보의 세계 $ U $에서 퍼지 집합 $ \ widetilde {A} $는 정렬 된 쌍 집합으로 정의 될 수 있으며 수학적으로 다음과 같이 표현 될 수 있습니다.

$$ \ widetilde {A} = \ left \ {\ left (y, \ mu _ {\ widetilde {A}} \ left (y \ right) \ right) | y \ in U \ right \} $$

여기서 $ \ mu _ {\ widetilde {A}} \ left (y \ right) $ = \ widetilde {A}에서 $ y $의 회원 등급, 0에서 1 사이의 값을 가정합니다. 즉, $ \ mu _ {\ widetilde {A}} (y) \ in \ left [0,1 \ right] $.

퍼지 세트 표현

이제 정보 우주의 두 가지 경우를 고려하고 퍼지 집합이 어떻게 표현 될 수 있는지 이해하겠습니다.

사례 1

정보의 우주 $ U $가 이산적이고 유한 할 때-

$$ \ widetilde {A} = \ left \ {\ frac {\ mu _ {\ widetilde {A}} \ left (y_1 \ right)} {y_1} + \ frac {\ mu _ {\ widetilde {A}} \ left (y_2 \ right)} {y_2} + \ frac {\ mu _ {\ widetilde {A}} \ left (y_3 \ right)} {y_3} + ... \ right \} $$

$ = \ left \ {\ sum_ {i = 1} ^ {n} \ frac {\ mu _ {\ widetilde {A}} \ left (y_i \ right)} {y_i} \ right \} $

사례 2

정보의 우주 $ U $가 연속적이고 무한 할 때-

$$ \ widetilde {A} = \ left \ {\ int \ frac {\ mu _ {\ widetilde {A}} \ left (y \ right)} {y} \ right \} $$

위의 표현에서 합계 기호는 각 요소의 컬렉션을 나타냅니다.

퍼지 세트에 대한 작업

두 개의 퍼지 세트 $ \ widetilde {A} $ 및 $ \ widetilde {B} $, 정보 유니버스 $ U $ 및 유니버스의 요소를 갖는 다음 관계는 퍼지 세트에 대한 결합, 교차 및 보완 연산을 표현합니다.

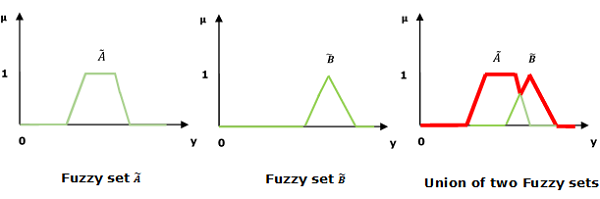
유니온 / 퍼지 'OR'

다음 표현을 고려하여 Union/Fuzzy ‘OR’ 관계 작품-

$$ \ mu _ {{\ widetilde {A} \ cup \ widetilde {B}}} \ left (y \ right) = \ mu _ {\ widetilde {A}} \ vee \ mu _ \ widetilde {B} \ 쿼드 \ forall y \ in U $$

여기서 ∨는 '최대'연산을 나타냅니다.

교차로 / 퍼지 'AND'

다음 표현을 고려하여 Intersection/Fuzzy ‘AND’ 관계 작품-

$$ \ mu _ {{\ widetilde {A} \ cap \ widetilde {B}}} \ left (y \ right) = \ mu _ {\ widetilde {A}} \ wedge \ mu _ \ widetilde {B} \ 쿼드 \ forall y \ in U $$

여기서 ∧는 'min'연산을 나타냅니다.

보완 / 퍼지 'NOT'

다음 표현을 고려하여 Complement/Fuzzy ‘NOT’ 관계 작품-

$$ \ mu _ {\ widetilde {A}} = 1- \ mu _ {\ widetilde {A}} \ left (y \ right) \ quad y \ in U $$

퍼지 세트의 속성

퍼지 세트의 다양한 속성에 대해 논의하겠습니다.

교환 재산

두 개의 퍼지 세트 $ \ widetilde {A} $ 및 $ \ widetilde {B} $가 있으면이 속성은 다음과 같이 나타납니다.

$$ \ widetilde {A} \ cup \ widetilde {B} = \ widetilde {B} \ cup \ widetilde {A} $$

$$ \ widetilde {A} \ cap \ widetilde {B} = \ widetilde {B} \ cap \ widetilde {A} $$

연관 속성

세 개의 퍼지 세트 $ \ widetilde {A} $, $ \ widetilde {B} $ 및 $ \ widetilde {C} $가 있으면이 속성은 다음과 같이 나타납니다.

$$ (\ widetilde {A} \ cup \ left \ widetilde {B}) \ cup \ widetilde {C} \ right = \ left \ widetilde {A} \ cup (\ widetilde {B} \ right) \ cup \ widetilde {C}) $$

$$ (\ widetilde {A} \ cap \ left \ widetilde {B}) \ cap \ widetilde {C} \ right = \ left \ widetilde {A} \ cup (\ widetilde {B} \ right \ cap \ widetilde { C}) $$

분배 재산

세 개의 퍼지 세트 $ \ widetilde {A} $, $ \ widetilde {B} $ 및 $ \ widetilde {C} $가 있으면이 속성은 다음과 같이 나타납니다.

$$ \ widetilde {A} \ cup \ left (\ widetilde {B} \ cap \ widetilde {C} \ right) = \ left (\ widetilde {A} \ cup \ widetilde {B} \ right) \ cap \ left (\ widetilde {A} \ cup \ widetilde {C} \ right) $$

$$ \ widetilde {A} \ cap \ left (\ widetilde {B} \ cup \ widetilde {C} \ right) = \ left (\ widetilde {A} \ cap \ widetilde {B} \ right) \ cup \ left (\ widetilde {A} \ cap \ widetilde {C} \ right) $$