Komunikacja cyfrowa - modulacja delta
Aby uzyskać lepsze próbkowanie, częstotliwość próbkowania sygnału powinna być wyższa niż częstotliwość Nyquista. Jeśli ten interwał próbkowania w różnicowym PCM zostanie znacznie zmniejszony, różnica amplitudy między próbkami jest bardzo mała, tak jakby różnica była1-bit quantization, wtedy rozmiar kroku będzie bardzo mały, tj. Δ (delta).
Modulacja delta
Rodzaj modulacji, w której częstotliwość próbkowania jest znacznie wyższa, a wielkość kroku po kwantyzacji ma mniejszą wartość Δ, taka modulacja jest określana jako delta modulation.
Cechy modulacji delta
Poniżej przedstawiono niektóre cechy modulacji delta.
Aby w pełni wykorzystać korelację sygnału, pobierane jest wejście z nadmierną próbkowaniem.
Projekt kwantyzacji jest prosty.
Sekwencja wejściowa jest znacznie wyższa niż współczynnik Nyquista.
Jakość jest umiarkowana.
Konstrukcja modulatora i demodulatora jest prosta.
Przybliżenie schodkowe przebiegu wyjściowego.
Wielkość kroku jest bardzo mała, tj. Δ (delta).
Użytkownik może zdecydować o szybkości transmisji.
Wymaga to prostszej implementacji.
Modulacja delta to uproszczona forma techniki DPCM, również postrzegana jako 1-bit DPCM scheme. Ponieważ interwał próbkowania jest zmniejszony, korelacja sygnału będzie wyższa.
Modulator delta
Modulator Delta składa się z 1-bitowego kwantyzatora i obwodu opóźniającego oraz dwóch obwodów letnich. Poniżej znajduje się schemat blokowy modulatora delta.
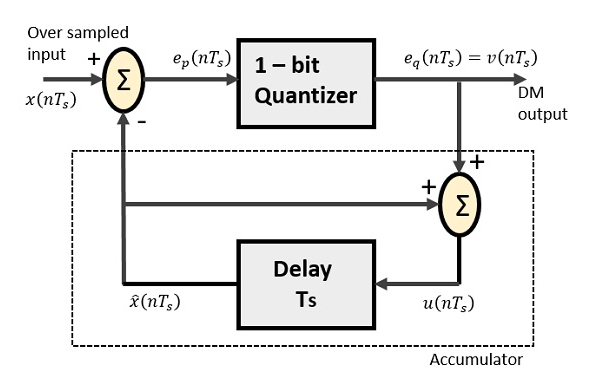
Obwód predykcyjny w DPCM jest zastąpiony prostym obwodem opóźniającym w DM.
Z powyższego schematu mamy zapisy jako -
$ x (nT_ {s}) $ = ponad próbkowane wejście
$ e_ {p} (nT_ {s}) $ = letnie wyjście i wejście kwantyzatora
$ e_ {q} (nT_ {s}) $ = wyjście kwantyzatora = $ v (nT_s) $
$ \ widehat {x} (nT_ {s}) $ = wyjście obwodu opóźniającego
$ u (nT_ {s}) $ = wejście obwodu opóźniającego
Korzystając z tych notacji, spróbujemy teraz rozgryźć proces modulacji delta.
$ e_ {p} (nT_ {s}) = x (nT_ {s}) - \ widehat {x} (nT_ {s}) $
--------- równanie 1
$ = x (nT_ {s}) - u ([n - 1] T_ {s}) $
$ = x (nT_ {s}) - [\ widehat {x} [[n - 1] T_ {s}] + v [[n-1] T_ {s}]] $
--------- równanie 2
Dalej,
$ v (nT_ {s}) = e_ {q} (nT_ {s}) = S.sig. [e_ {p} (nT_ {s})] $
--------- równanie 3
$ u (nT_ {s}) = \ widehat {x} (nT_ {s}) + e_ {q} (nT_ {s}) $
Gdzie,
$ \ widehat {x} (nT_ {s}) $ = poprzednia wartość obwodu opóźniającego
$ e_ {q} (nT_ {s}) $ = wyjście kwantyzatora = $ v (nT_s) $
W związku z tym,
$ u (nT_ {s}) = u ([n – 1] T_ {s}) + v (nT_ {s}) $
--------- równanie 4
Co znaczy,
The present input of the delay unit
= (The previous output of the delay unit) + (the present quantizer output)
Zakładając zerowy warunek akumulacji,
$ u (nT_ {s}) = S \ Displaystyle \ suma \ limity_ {j = 1} ^ n sig [e_ {p} (jT_ {s})] $
Accumulated version of DM output = $ \ Displaystyle \ suma \ limity_ {j = 1} ^ nv (jT_ {s}) $
--------- równanie 5
Teraz zauważ to
$ \ widehat {x} (nT_ {s}) = u ([n – 1] T_ {s}) $
$ = \ Displaystyle \ suma \ limity_ {j = 1} ^ {n - 1} v (jT_ {s}) $
--------- równanie 6
Wyjście jednostki opóźnienia to wyjście z akumulatora opóźnione o jedną próbkę.
Z równań 5 i 6 otrzymujemy możliwą strukturę demodulatora.
Przybliżony przebieg schodkowy będzie sygnałem wyjściowym modulatora delta z wielkością kroku równą delta (Δ). Jakość wyjściowa przebiegu jest umiarkowana.
Delta Demodulator
Demodulator delta składa się z filtra dolnoprzepustowego, obwodu letniego i obwodu opóźniającego. Obwód predykcyjny jest tutaj wyeliminowany, a zatem żadne założone dane wejściowe nie są podawane do demodulatora.
Poniżej znajduje się schemat demodulatora delta.
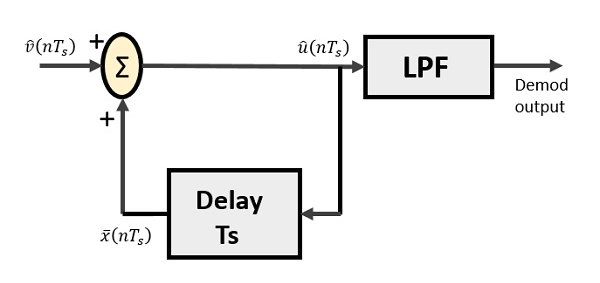
Z powyższego schematu mamy zapisy jako -
$ \ widehat {v} (nT_ {s}) $ jest próbką wejściową
$ \ widehat {u} (nT_ {s}) $ to letnie wyjście
$ \ bar {x} (nT_ {s}) $ to opóźnione wyjście
Jako dane wejściowe do demodulatora zostanie podana sekwencja binarna. Przybliżona moc wyjściowa klatki schodowej jest podawana do LPF.
Filtr dolnoprzepustowy jest używany z wielu powodów, ale głównym powodem jest eliminacja szumów dla sygnałów pozapasmowych. Nazywa się błąd wielkości kroku, który może wystąpić w nadajnikugranular noise, co jest tutaj wyeliminowane. Jeśli nie ma szumu, wyjście modulatora jest równe wejściu demodulatora.
Zalety DM w porównaniu z DPCM
1-bitowy kwantyzator
Bardzo łatwa konstrukcja modulatora i demodulatora
Jednak w DM występuje pewien szum.
Zniekształcenie nachylenia nad obciążeniem (kiedy Δ jest mały)
Ziarnisty hałas (kiedy Δ jest wielki)
Adaptacyjna modulacja delta (ADM)
W modulacji cyfrowej natknęliśmy się na pewien problem określenia wielkości kroku, który wpływa na jakość fali wyjściowej.
W przypadku stromego zbocza sygnału modulującego wymagany jest większy rozmiar kroku, a mniejszy rozmiar kroku jest potrzebny, gdy komunikat ma małe nachylenie. W trakcie procesu pomijane są najdrobniejsze szczegóły. Byłoby więc lepiej, gdybyśmy mogli kontrolować regulację wielkości kroku, zgodnie z naszymi wymaganiami, aby uzyskać próbkowanie w pożądany sposób. To jest koncepcjaAdaptive Delta Modulation.
Poniżej przedstawiono schemat blokowy Adaptacyjnego modulatora delta.
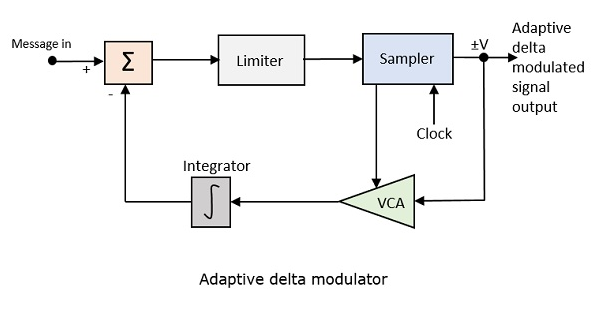
Wzmocnienie wzmacniacza sterowanego napięciem jest regulowane sygnałem wyjściowym z próbnika. Wzmocnienie wzmacniacza określa wielkość kroku i oba są proporcjonalne.
ADM kwantyfikuje różnicę między wartością bieżącej próbki a przewidywaną wartością następnej próbki. Wykorzystuje zmienną wysokość kroku do przewidywania kolejnych wartości w celu wiernego odtworzenia szybko zmieniających się wartości.