Komunikacja cyfrowa - kody linii
ZA line codejest kodem używanym do transmisji danych sygnału cyfrowego przez linię transmisyjną. Ten proces kodowania jest wybrany tak, aby uniknąć nakładania się i zniekształcania sygnału, takiego jak interferencja między symbolami.
Właściwości kodowania linii
Poniżej przedstawiono właściwości kodowania liniowego -
Ponieważ kodowanie ma na celu przesłanie większej liczby bitów w jednym sygnale, wykorzystywana szerokość pasma jest znacznie zmniejszona.
Dla danej przepustowości moc jest efektywnie wykorzystywana.
Prawdopodobieństwo błędu jest znacznie ograniczone.
Wykonywane jest wykrywanie błędów, a dwubiegunowy również ma możliwość korekcji.
Gęstość mocy jest bardzo korzystna.
Treść czasowa jest odpowiednia.
Długie sznurki 1s i 0s w celu zachowania przejrzystości.
Rodzaje kodowania linii
Istnieją 3 rodzaje kodowania linii
- Unipolar
- Polar
- Bi-polar
Sygnalizacja jednobiegunowa
Sygnalizacja jednobiegunowa jest również nazywana as On-Off Keying lub po prostu OOK.
Obecność impulsu oznacza a 1 a brak impulsu oznacza a 0.
Istnieją dwie odmiany sygnalizacji jednobiegunowej -
- Bez powrotu do zera (NRZ)
- Powrót do zera (RZ)
Unipolar Non-Return to Zero (NRZ)
W tego typu sygnalizacji jednobiegunowej wysoki w danych jest reprezentowany przez dodatni impuls nazywany as Mark, który ma czas trwania T0równy czasowi trwania bitu symbolu. Niski poziom danych wejściowych nie ma impulsu.
Poniższy rysunek wyraźnie to ilustruje.
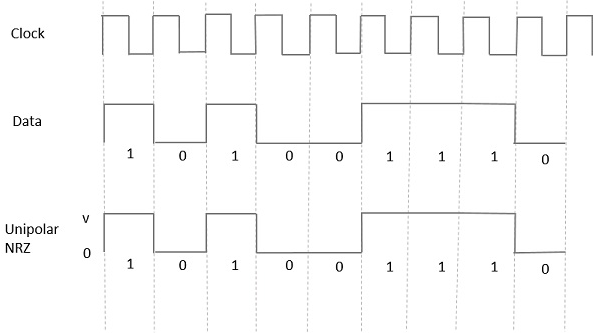
Advantages
Zalety Unipolar NRZ to -
- To jest proste.
- Wymagana jest mniejsza przepustowość.
Disadvantages
Wady Unipolar NRZ to -
Nie wykonano korekcji błędów.
Obecność składowych o niskiej częstotliwości może spowodować zanik sygnału.
Brak zegara.
Może wystąpić utrata synchronizacji (szczególnie w przypadku długich ciągów 1s i 0s).
Jednobiegunowy powrót do zera (RZ)
W tym typie sygnalizacji jednobiegunowej, wysoki w danych, chociaż reprezentowany przez Mark pulse, czas jego trwania T0jest krótszy niż czas trwania bitu symbolu. Połowa czasu trwania bitu pozostaje wysoka, ale natychmiast powraca do zera i pokazuje brak impulsu podczas pozostałej połowy czasu trwania bitu.
Jest to wyraźnie zrozumiałe na podstawie poniższego rysunku.
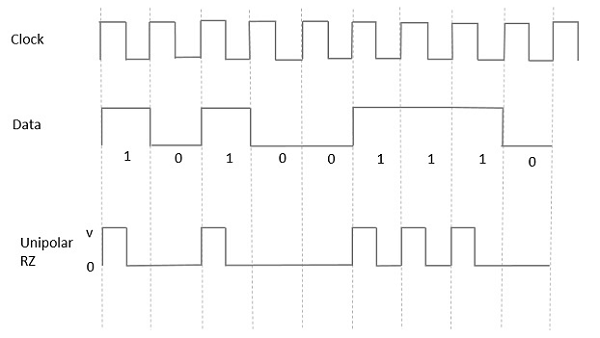
Advantages
Zalety Unipolar RZ to -
- To jest proste.
- Linia widmowa obecna przy szybkości transmisji symboli może służyć jako zegar.
Disadvantages
Wady Unipolar RZ to -
- Brak korekcji błędów.
- Zajmuje dwukrotnie większą przepustowość niż unipolarny NRZ.
- Stłumienie sygnału jest powodowane w miejscach, w których sygnał jest niezerowy przy 0 Hz.
Sygnalizacja biegunowa
Istnieją dwie metody sygnalizacji biegunowej. Oni są -
- Polar NRZ
- Polar RZ
Polar NRZ
W tego typu sygnalizacji biegunowej wysoki poziom danych jest reprezentowany przez dodatni impuls, a niski w danych jest reprezentowany przez impuls ujemny. Poniższy rysunek dobrze to przedstawia.
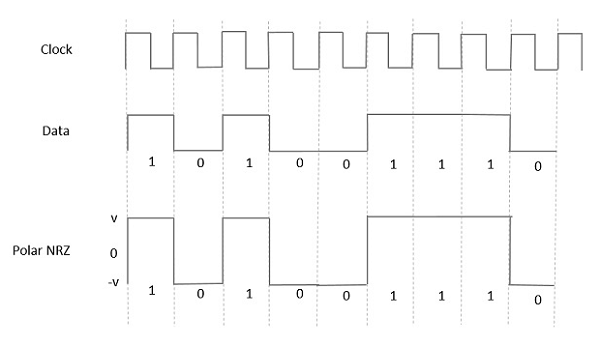
Advantages
Zalety Polar NRZ to -
- To jest proste.
- Brak elementów o niskiej częstotliwości.
Disadvantages
Wady Polar NRZ to -
Brak korekcji błędów.
Brak zegara.
Spadek sygnału jest spowodowany w miejscach, w których sygnał jest niezerowy w 0 Hz.
Polar RZ
W tego typu sygnalizacji biegunowej, wysoki w danych, chociaż reprezentowany przez Mark pulse, czas jego trwania T0jest krótszy niż czas trwania bitu symbolu. Połowa czasu trwania bitu pozostaje wysoka, ale natychmiast powraca do zera i pokazuje brak impulsu podczas pozostałej połowy czasu trwania bitu.
Jednak dla wejścia Low, ujemny impuls reprezentuje dane, a poziom zerowy pozostaje taki sam przez drugą połowę czasu trwania bitu. Poniższy rysunek wyraźnie to ilustruje.
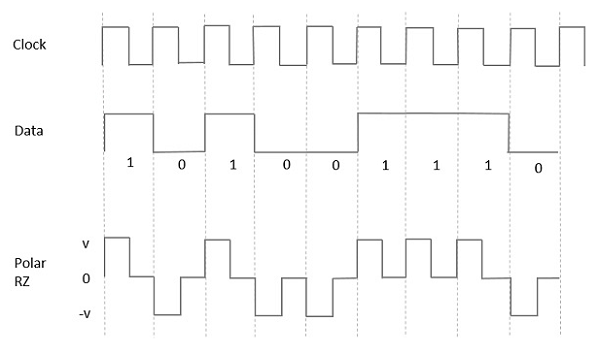
Advantages
Zalety Polar RZ to -
- To jest proste.
- Brak elementów o niskiej częstotliwości.
Disadvantages
Wady Polar RZ to -
Brak korekcji błędów.
Brak zegara.
Zajmuje dwukrotnie większą przepustowość niż Polar NRZ.
Spadek sygnału jest spowodowany w miejscach, w których sygnał jest niezerowy w 0 Hz.
Sygnalizacja bipolarna
Jest to technika kodowania, która ma trzy poziomy napięcia, a mianowicie +, - i 0. Taki sygnał nazywa sięduo-binary signal.
Przykładem tego typu jest Alternate Mark Inversion (AMI). Dla1poziom napięcia przechodzi od + do - lub od - do +, na przemian 1smieć równą biegunowość. ZA0 będzie miał zerowy poziom napięcia.
Nawet w tej metodzie mamy dwa typy.
- Bipolarny NRZ
- Bipolarny RZ
Z dotychczas omówionych modeli poznaliśmy różnicę między NRZ a RZ. Tutaj też jest tak samo. Poniższy rysunek wyraźnie to ilustruje.
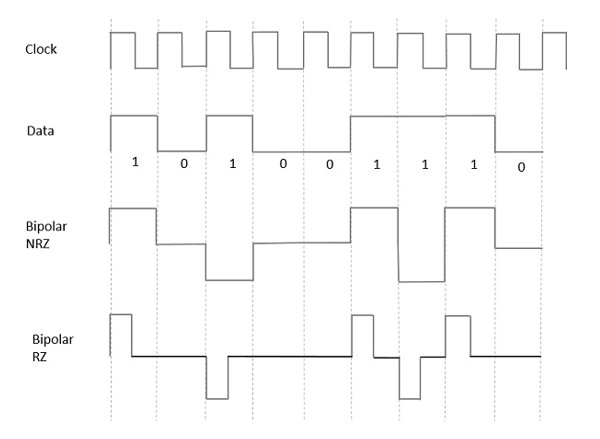
Powyższy rysunek ma zarówno przebiegi bipolarne NRZ, jak i RZ. Czas trwania impulsu i czas trwania bitu symbolu są równe w typie NRZ, podczas gdy czas trwania impulsu jest równy połowie czasu trwania bitu symbolu w typie RZ.
Zalety
Oto zalety -
To jest proste.
Brak elementów o niskiej częstotliwości.
Zajmuje niską przepustowość niż jednobiegunowe i polarne schematy NRZ.
Technika ta jest odpowiednia do transmisji przez linie sprzężone z prądem przemiennym, ponieważ nie występuje tutaj opadanie sygnału.
Jest w tym obecna możliwość wykrywania pojedynczego błędu.
Niedogodności
Oto wady -
- Brak zegara.
- Długie ciągi danych powodują utratę synchronizacji.
Gęstość widmowa mocy
Funkcja, która opisuje, w jaki sposób moc sygnału została rozłożona na różnych częstotliwościach w dziedzinie częstotliwości, nazywa się as Power Spectral Density (PSD).
PSD to transformata Fouriera autokorelacji (podobieństwo między obserwacjami). Ma postać prostokątnego impulsu.
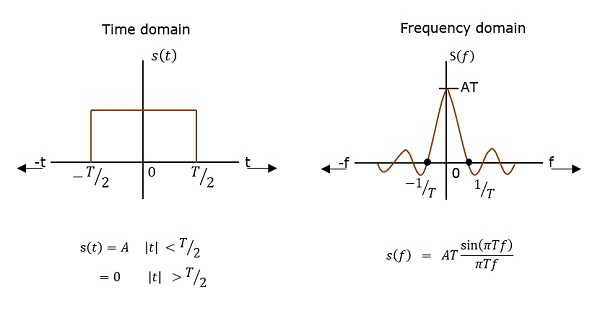
Wyprowadzenie PSD
Zgodnie z twierdzeniem Einsteina-Wienera-Khintchine'a, jeśli znana jest funkcja autokorelacji lub gęstość widmowa mocy procesu losowego, drugą można dokładnie znaleźć.
Stąd, aby otrzymać gęstość widmową mocy, użyjemy autokorelacji czasowej $ (R_x (\ tau)) $ sygnału mocy $ x (t) $, jak pokazano poniżej.
$ R_x (\ tau) = \ lim_ {T_p \ rightarrow \ infty} \ frac {1} {T_p} \ int _ {\ frac {{- T_p}} {2}} ^ {\ frac {T_p} {2}} x (t) x (t + \ tau) dt $
Ponieważ $ x (t) $ składa się z impulsów, $ R_x (\ tau) $ można zapisać jako
$ R_x (\ tau) = \ Frac {1} {T} \ Displaystyle \ suma \ limit_ {n = - \ infty} ^ \ infty R_n \ delta (\ tau - nT) $
Gdzie $ R_n = \ lim_ {N \ rightarrow \ infty} \ frac {1} {N} \ sum_ka_ka_ {k + n} $
Dowiadując się, że $ R_n = R _ {- n} $ dla rzeczywistych sygnałów, mamy
$ S_x (w) = \ Frac {1} {T} (R_0 + 2 \ Displaystyle \ suma \ limity_ {n = 1} ^ \ infty R_n \ cos nwT) $
Ponieważ filtr impulsowy ma widmo $ (w) \ leftrightarrow f (t) $, mamy
$ s_y (w) = \ mid F (w) \ mid ^ 2S_x (w) $
$ = \ Frac {\ mid F (w) \ mid ^ 2} {T} (\ Displaystyle \ sum \ limity_ {n = - \ infty} ^ \ infty R_ne ^ {- jnwT_ {b}}) $
$ = \ Frac {\ mid F (w) \ mid ^ 2} {T} (R_0 + 2 \ Displaystyle \ suma \ limity_ {n = 1} ^ \ infty R_n \ cos nwT) $
Stąd otrzymujemy równanie na gęstość widmową mocy. Korzystając z tego, możemy znaleźć PSD różnych kodów linii.