Komunikacja cyfrowa - próbkowanie
Sampling definiuje się jako „proces pomiaru chwilowych wartości sygnału w czasie ciągłym w formie dyskretnej”.
Sample to fragment danych pobrany z całych danych, który jest ciągły w dziedzinie czasu.
Kiedy źródło generuje sygnał analogowy i jeśli ma on zostać zdigitalizowany, posiadanie 1s i 0stj. wysoki lub niski, sygnał musi być dyskretyzowany w czasie. Ta dyskretyzacja sygnału analogowego nazywana jest próbkowaniem.
Poniższy rysunek przedstawia ciągły sygnał czasu x (t) i próbkowany sygnał xs (t). Gdyx (t) jest mnożony przez okresowy ciąg impulsów, próbkowany sygnał xs (t) jest uzyskiwane.
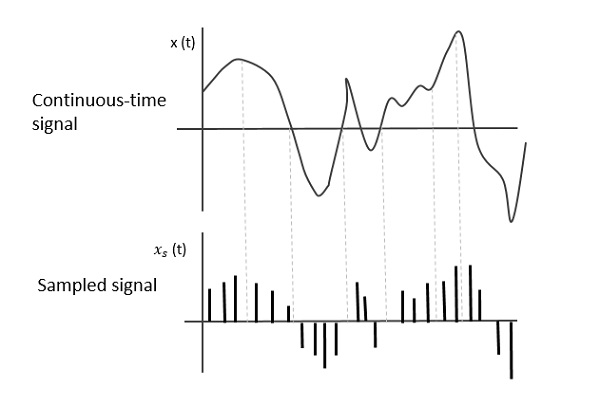
Częstotliwość próbkowania
Aby zdyskretyzować sygnały, należy naprawić odstęp między próbkami. Ta luka może być określona jakosampling period Ts.
$$ Próbkowanie \: Częstotliwość = \ frac {1} {T_ {s}} = f_s $$Gdzie,
$ T_ {s} $ to czas próbkowania
$ f_ {s} $ to częstotliwość próbkowania lub częstotliwość próbkowania
Sampling frequencyjest odwrotnością okresu pobierania próbek. Tę częstotliwość próbkowania można po prostu nazwać jakoSampling rate. Częstotliwość próbkowania oznacza liczbę próbek pobieranych na sekundę lub dla skończonego zestawu wartości.
Aby sygnał analogowy mógł zostać zrekonstruowany z sygnału cyfrowego, należy dokładnie rozważyć częstotliwość próbkowania. Częstotliwość próbkowania powinna być taka, aby dane w sygnale komunikatu nie zostały utracone ani nie zostały nałożone. W związku z tym ustalono dla tego stawkę, zwaną stopą Nyquista.
Nyquist Rate
Załóżmy, że sygnał jest ograniczony pasmem bez składowych częstotliwości wyższych niż WHerc. To znaczy,Wto najwyższa częstotliwość. W przypadku takiego sygnału, aby skutecznie odtworzyć pierwotny sygnał, częstotliwość próbkowania powinna być dwukrotnie większa od najwyższej częstotliwości.
Co znaczy,
$$ f_ {S} = 2W $$Gdzie,
$ f_ {S} $ to częstotliwość próbkowania
W to najwyższa częstotliwość
Ta częstotliwość próbkowania jest nazywana jako Nyquist rate.
Twierdzenie zwane Twierdzeniem o próbkowaniu zostało sformułowane na podstawie teorii współczynnika Nyquista.
Twierdzenie o próbkowaniu
Twierdzenie o próbkowaniu, które jest również nazywane as Nyquist theorem, dostarcza teorii wystarczającej częstotliwości próbkowania pod względem szerokości pasma dla klasy funkcji o ograniczonym paśmie.
Twierdzenie o próbkowaniu stwierdza, że „sygnał może być dokładnie odtworzony, jeśli jest próbkowany z określoną częstotliwością fs która jest większa niż dwukrotność maksymalnej częstotliwości W. ”
Aby zrozumieć to twierdzenie o próbkowaniu, rozważmy sygnał o ograniczonym paśmie, tj. Sygnał, którego wartość jest równa non-zero między niektórymi –W i W Herc.
Taki sygnał jest reprezentowany jako $x(f) = 0 for |f\lvert > W$
Dla sygnału czasu ciągłego x (t), sygnał o ograniczonym paśmie w dziedzinie częstotliwości, można przedstawić w sposób pokazany na poniższym rysunku.
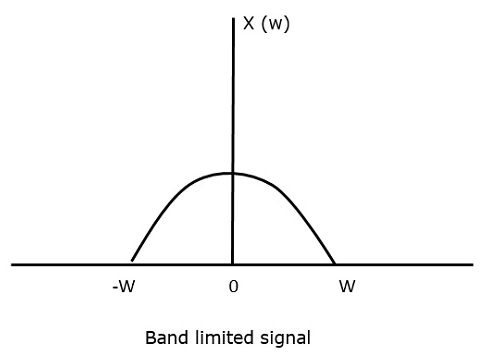
Potrzebujemy częstotliwości próbkowania, częstotliwości, przy której nie powinno być utraty informacji, nawet po próbkowaniu. W tym celu mamy współczynnik Nyquista, zgodnie z którym częstotliwość próbkowania powinna być dwukrotnie większa od częstotliwości maksymalnej. Jest to krytyczna częstotliwość pobierania próbek.
Jeśli sygnał x(t) jest próbkowany powyżej częstotliwości Nyquista, pierwotny sygnał można odzyskać, a jeśli jest próbkowany poniżej częstotliwości Nyquista, sygnału nie można odzyskać.
Poniższy rysunek wyjaśnia sygnał, jeśli próbkowany jest z większą częstotliwością niż 2w w dziedzinie częstotliwości.
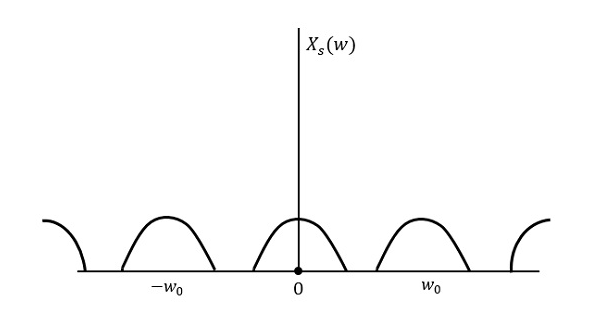
Powyższy rysunek przedstawia transformatę Fouriera sygnału $x_{s}(t)$. Tutaj informacje są odtwarzane bez żadnych strat. Nie ma pomieszania, a zatem możliwy jest powrót do zdrowia.
Transformacja Fouriera sygnału $x_{s}(t)$ jest
$$ X_ {s} (w) = \ frac {1} {T_ {s}} \ sum_ {n = - \ infty} ^ \ infty X (w-nw_0) $$Gdzie $ T_ {s} $ = Sampling Period i $ w_ {0} = \ frac {2 \ pi} {T_s} $
Zobaczmy, co się stanie, jeśli częstotliwość próbkowania jest równa dwukrotności najwyższej częstotliwości (2W)
To znaczy,
$$ f_ {s} = 2W $$Gdzie,
$ f_ {s} $ to częstotliwość próbkowania
W to najwyższa częstotliwość
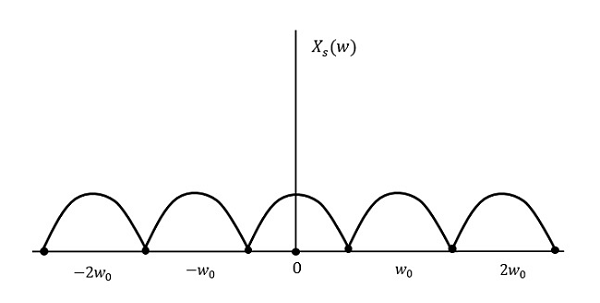
Wynik będzie taki, jak pokazano na powyższym rysunku. Informacje są wymieniane bez żadnych strat. W związku z tym jest to również dobra częstotliwość próbkowania.
Spójrzmy teraz na stan,
$$ f_ {s} <2W $$Powstały wzór będzie wyglądał jak na poniższym rysunku.

Z powyższego schematu możemy zauważyć, że zachodzi nakładanie się informacji, co prowadzi do pomieszania i utraty informacji. To niepożądane zjawisko nakładania się nosi nazwę aliasingu.
Aliasing
Aliasing można określić jako „zjawisko składowej o wysokiej częstotliwości w widmie sygnału, przyjmujące tożsamość składowej o niskiej częstotliwości w widmie jego próbkowanej wersji”.
Środki naprawcze podjęte w celu zmniejszenia efektu aliasingu to:
W sekcji nadajnika PCM a low pass anti-aliasing filter jest stosowany przed próbnikiem w celu wyeliminowania niepożądanych składowych o wysokiej częstotliwości.
Sygnał, który jest próbkowany po filtrowaniu, jest próbkowany z częstotliwością nieco wyższą niż częstotliwość Nyquista.
Ten wybór częstotliwości próbkowania wyższej niż częstotliwość Nyquista pomaga również w łatwiejszym projektowaniu reconstruction filter na odbiorniku.
Zakres transformacji Fouriera
Powszechnie obserwuje się, że w analizie sygnałów, a także w dowodzeniu twierdzeń, korzystamy z szeregu Fouriera i transformacji Fouriera. To dlatego, że -
Transformacja Fouriera jest przedłużeniem szeregu Fouriera dla sygnałów nieperiodycznych.
Transformata Fouriera to potężne narzędzie matematyczne, które pomaga przeglądać sygnały w różnych dziedzinach i ułatwia ich analizę.
Każdy sygnał można rozłożyć na sumę sinusów i cosinusów za pomocą tej transformaty Fouriera.
W następnym rozdziale omówimy pojęcie kwantyzacji.