Twierdzenie o kodowaniu źródłowym
Kod wytwarzany przez dyskretne źródło bez pamięci musi być skutecznie reprezentowany, co jest ważnym problemem w komunikacji. Aby tak się stało, istnieją słowa kodowe, które reprezentują te kody źródłowe.
Na przykład w telegrafii używamy alfabetu Morse'a, w którym alfabety są oznaczone Marks i Spaces. Jeśli listE jest brany pod uwagę, który jest najczęściej używany, jest oznaczony przez “.” Natomiast list Q który jest rzadko używany, jest oznaczony przez “--.-”
Przyjrzyjmy się diagramowi blokowemu.
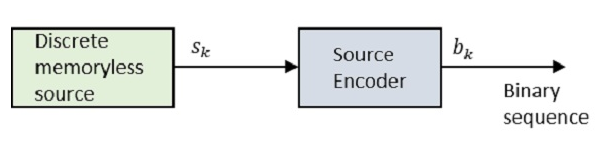
Gdzie Sk jest wyjściem dyskretnego źródła bez pamięci i bk jest wyjściem kodera źródłowego, które jest reprezentowane przez 0s i 1s.
Zakodowana sekwencja jest taka, że jest dogodnie dekodowana w odbiorniku.
Załóżmy, że źródło ma alfabet z k różne symbole i że kth symbol Sk występuje z prawdopodobieństwem Pk, gdzie k = 0, 1…k-1.
Niech binarne słowo kodowe przypisane do symbolu Sk, przez koder mający długość lk, mierzona w bitach.
Dlatego definiujemy średnią długość L słowa kodowego kodera źródłowego jako
$$ \ overline {L} = \ Displaystyle \ sum \ limits_ {k = 0} ^ {k-1} p_kl_k $$
L reprezentuje średnią liczbę bitów na symbol źródłowy
Jeśli $ L_ {min} = \: minimum \: możliwe \: wartość \: z \: \ overline {L} $
Następnie coding efficiency można zdefiniować jako
$$ \ eta = \ frac {L {min}} {\ overline {L}} $$
Z $ \ overline {L} \ geq L_ {min} $ będziemy mieć $ \ eta \ leq 1 $
Jednak koder źródłowy jest uważany za wydajny, gdy $ \ eta = 1 $
W tym celu należy określić wartość $ L_ {min} $.
Odwołajmy się do definicji: „Biorąc pod uwagę dyskretne, pozbawione pamięci źródło entropii $ H (\ delta) $, średnia długość słowa kodowegoL dla dowolnego kodowania źródłowego jest ograniczone jako $ \ overline {L} \ geq H (\ delta) $. "
Mówiąc prościej, słowo kodowe (przykład: kod Morse'a dla słowa QUEUE to -.- ..-. ..-.) Jest zawsze większe lub równe kodowi źródłowemu (na przykład QUEUE). Co oznacza, że symbole w słowie kodowym są większe lub równe alfabetom w kodzie źródłowym.
Stąd z $ L_ {min} = H (\ delta) $, wydajność kodera źródłowego w kategoriach Entropii $ H (\ delta) $ można zapisać jako
$$ \ eta = \ frac {H (\ delta)} {\ overline {L}} $$
To twierdzenie o kodowaniu źródłowym nazywa się as noiseless coding theoremponieważ zapewnia wolne od błędów kodowanie. Nazywa się to również jakoShannon’s first theorem.